控制理论的三个发展阶段:经典控制理论、现代控制理论、智能控制理论
- 格式:docx
- 大小:20.67 KB
- 文档页数:1

第一章绪论1.自动控制理论的三个发展阶段是(经典控制理论、现代控制理论、智能控制理论)2.偏差量指的是(给定量)与反馈量相减后的输出量3.负反馈是指将系统的(输出量)直接或经变换后引入输入端,与(输入量)相减,利用所得的(偏差量)去控制被控对象,达到减少偏差或消除偏差的目的。
4.对控制系统的基本要求有(稳定性、快速性、准确性)5.稳定性是系统正常工作的必要条件,,要求系统稳态误差(要小)6.快速性要求系统快速平稳地完成暂态过程,超调量(要小),调节时间(要短)7.自动控制理论的发展进程是(经典控制理论、现代控制理论、智能控制理论)8.经典控制理论主要是以(传递函数)为基础,研究单输入单输出系统的分析和设计问题第二章自动控制系统的数学模型1.数学模型是描述系统输出量,输入量及系统各变量之间关系的(数学表达式)2.传递函数的分母多项式即为系统的特征多项式,令多项式为零,即为系统的特征方程式,特征方程式的根为传递函数的(极点),分子的形式的根是传递函数的(零点)3. 惯性环节的传递函数为(11+Ts ) 4. 惯性环节的微分方程为(T)()(t d t dc +c (t)=r(t) 5. 振荡环节的传递函数为(G (s )=nn s s 2222ωζωω++)6. 系统的开环传递函数为前向通道的传递函数与反馈通道的传递函数的(乘积)7. 信号流图主要由(节点和支路)两部分组成8. 前向通道为从输入节点开始到输出节点终止,且每个节点通过(一次)的通道9. 前向通道增益等于前向通道中各个支路增益的(乘积)10. 在线性定常系统中,当初始条件为零时,系统输出的拉氏变换与输入的拉氏变换之比称作系统的(传递函数)11. 传递函数表示系统传递,变换输入信号的能力,只与(结构和参数)有关,与(输入输出信号形式)无关12. 信号流图主要由两部分组成:节点和支路,下面有关信号流图的术语中,正确的是(B )A . 节点表示系统中的变量或信号B .支路是连接两个节点的有向线段,支路上的箭头表示传递的方向,传递函数标在支路上 C .只有输出支路的节点称为输入节点,只有输入支路的节点为输出节点,既有输入支路又有输出支路的节点称为混合节点 D . 前向通道为从输入节点开始到输出节点终止,且每个节点通过(一次)的通道,前向通道增益等于前向通道中各个支路增益的乘积13. 求图示无源网络的传递函数U 。

经典控制理论是以传递函数为基础的一种控制理论,控制系统的分析与设计是建立在某种近似的和(或)试探的基础上的、控制对象一般是单输入单输出、线性定常系统;对多输入多输出系统、时变系统、非线性系统等.则无能为力。
经典抑制理论主要的分析方法有频率特性分析法、根轨迹分析法、描述函数法、相平面法、波波夫法等。
控制策略仅局限于反馈控制、PID控制等。
这种控制不能实现最优控制。
现代控制理论是建立在状态空间上的一种分析方法,它的数学模型主要是状态方程,控制系统的分析与设计是精确的。
控制对象可以是单输入单输出控制系统.也可以是多输人多输出控制系统,可以是线件定常控制系统,也可以是非线性时变控制系统,可以是连续控制系统,也可以是离散和(或)数字控制系统。
因此,现代控制理论的应用范围更加广泛。
主要的控制策略有极点配置、状态反馈、输出反馈等。
由于现代控制理论的分析与设计方法的精确性,因此,现代控制可以得到最优控制。
但这些控制策略大多是建立在已知系统的基础之上的。
严格来说.大部分的控制系统是一个完全未知或部分未知系统,这里包括系统本身参数未知、系统状态未知两个方面,同时被控制对象还受外界干扰、环境变化等的因素影响。
智能控制是一种能更好地模仿人类智能的、非传统的控制方法,它采用的理论方法则主要来自自动控制理论、人工智能和运筹学等学科分支。
内容包括最优控制、自适应控制、鲁棒控制、神经网络控制、模糊控制、仿人控制等。
其控制对象可以是已知系统也可以是未知系统,大多数的控制策略不仅能抑制外界干扰、环境变化、参数变化的影响,还能有效地消除模型化误差的影响。

控制理论与控制系统的发展历史及趋势姓名:学号:指导教师:专业:所在学院:机电工程学院时间:2011年11月3号控制理论与控制系统的发展历史及趋势摘要:由于自动控制理论和自动控制系统的的广泛运用,各行业的专业人员对它的学习,研究也在不断的进行。
本文叙述了自动控制理论和自动控制系统的发展历史(三个阶段:经典控制,现代控制,智能控制)和发展的趋势。
前言控制是人类对事物的认识思考,进而作出决策并作出相应反应的过程。
人类在漫长的生产与生活实践中不断总结,积累经验,形成理论,进而指导实践使生产力不断发展。
随着生产力的不断发展,人们开始要求生活的高质量,一方面要从繁重的体力劳动中解放自己,另一方面要有更高质量的产品来满足生活的需要。
自动控制理论自动控制系统就随之而产生了。
控制理论和控制系统经过漫长的发展,其研究范围和应用范围很广泛。
控制理论研究的对象和应用领域不但涉及到工业、农业、交通、运输等传统产业,还涉及到生物、通讯、信息、管理等新兴行业。
由于自动控制理论和自动控制系统获得了如此广泛的应用,所以自动控制的发展必将受到各行各业的关注。
本文就是对控制理论和控制系统的发展历史进行综述,叙述控制发展的各个阶段。
还有就是控制理论和控制系统的今后的发展趋势。
一,控制理论的发展历史及趋势1,早期的自动控制装置及自动控制技术的形成古代人类在长期生产和生活中,为了减轻自己的劳动,逐渐产生利用自然界动力代替人力畜力,以及用自动装置代替人的部分繁难的脑力活动的愿望,经过漫长岁月的探索,他们互不相关地造出一些原始的自动装置。
约在公元前三世纪中叶,亚历山大里亚城的斯提西比乌斯首先在受水壶中使用了浮子。
按迪尔斯(Diels)本世纪初复原的样品,注入的水是由圆锥形的浮子节制的。
而这种节制方式即已含有负反馈的思想(尽管当时并不明确)。
公元前500年,中国的军队中即已用漏壶作为计时的装置。
约在公元120年,著名的科学家张衡(78-139,东汉)又提出了用补偿壶解决随水头降低计时不准确问题的巧妙方法。
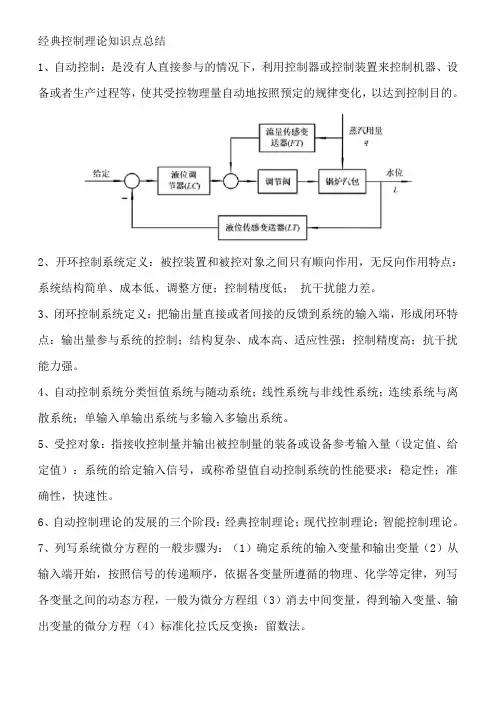
经典控制理论知识点总结1、自动控制:是没有人直接参与的情况下,利用控制器或控制装置来控制机器、设备或者生产过程等,使其受控物理量自动地按照预定的规律变化,以达到控制目的。
2、开环控制系统定义:被控装置和被控对象之间只有顺向作用,无反向作用特点:系统结构简单、成本低、调整方便;控制精度低;抗干扰能力差。
3、闭环控制系统定义:把输出量直接或者间接的反馈到系统的输入端,形成闭环特点:输出量参与系统的控制;结构复杂、成本高、适应性强;控制精度高;抗干扰能力强。
4、自动控制系统分类恒值系统与随动系统;线性系统与非线性系统;连续系统与离散系统;单输入单输出系统与多输入多输出系统。
5、受控对象:指接收控制量并输出被控制量的装备或设备参考输入量(设定值、给定值):系统的给定输入信号,或称希望值自动控制系统的性能要求:稳定性;准确性,快速性。
6、自动控制理论的发展的三个阶段:经典控制理论;现代控制理论;智能控制理论。
7、列写系统微分方程的一般步骤为:(1)确定系统的输入变量和输出变量(2)从输入端开始,按照信号的传递顺序,依据各变量所遵循的物理、化学等定律,列写各变量之间的动态方程,一般为微分方程组(3)消去中间变量,得到输入变量、输出变量的微分方程(4)标准化拉氏反变换:留数法。
8、传递函数的定义:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比,称为线性定常系统的传递函数微分方程在时间域,传递函数在复数域传递函数的性质传递函数只适用于线性定常系统;传递函数是在零初始条件下定义的;传递函数可以有量纲;传递函数表示系统的端口关系;传递函数描述了系统的固有特性传递函数的表达式有理分式形式(特征多项式型)零、极点形式(首一型)时间常数形式(尾一型)。
9、动态性能的五个指标延迟时间(稳态值50%);上升时间(稳态值10%-90%,非一阶0-稳态值);峰值时间;调节时间;超调量(或最大超调量)。
10、一阶单位阶跃系统的动态性能指标:调节时间t=3T(5%误差带),t=4T(2%误差带)延迟时间t=0.69T上升时间t=2.20T峰值时间,超调量不存欠阻尼二阶系统的动态性能指标(P72)一对靠的很近或相等的零、极点,彼此将相互抵消,其结果使留数等于零,此类零、极点称为偶极子闭环主导极点,它应满足以下两个条件:(1)在s平面上,距离虚轴比较近,且附近没有其他的零点和极点(2)其实部的绝对值比其他极点实部的绝对值小5倍以上。






自动控制理论的发展及其应用综述黄佳彬312010122420世纪40年代,控制论这门学科开始发展,其标志为维纳于1948年出版7自动控制学科史上的名著《控制论,或动物和机器的控制和通信XCybernetics, or control and conunuiiication ill the animal and machine )。
控制论思想的提出为现代科学研究提供了新的思想和方法,同时书中的一些新颖的思想和观点吸引了无数学者,令其在自己研究的领域引进控制论。
随着研究队伍的庞大,控制论形成了多个分支,其中主要的儿个分支有生物控制论,工程控制论,军事控制论,社会、经济控制论,自然控制论。
这里我们主要对工程控制论进行研究。
1.自动控制理论的发展工程控制论的概念最早山钱学森引入,当时有两种控制理论思想,一种基于时间域微分方程,另一种基于系统的频率特性。
这两种思想即为经典控制理论, 主要研究的是单输入-单输出的控制系统,同时利用分析法与实验验证法这两种方法对某个控制系统进行数学建模,山此可以获得系统各元部件之间的信号传递关系的形象表示。
由于经典控制理论的建立基于传递函数和频率特性,是对系统的外部描述。
同时经典控制理论主要研究单输入单输出系统,无法解决现实工程应用中多输入多输出系统的问题,而且经典控制理论只对线性时不变系统进行讨论,存在不少的局限性,由此,现代控制理论逐渐发展起来。
现代控制理论是从线性代数的理论研究上得来的,本质是“时域法”,即基于状态空间模型在时域对系统进行分析和设计,并且引入“状态”这一概念,用“状态变量”和“状态方程”描述系统,以此来反应系统的内在本质和特性。
现代控制理论研究的内容主要有三方面:多变量线性系统理论、最优控制理论以及最优估计与系统辨识理论,这些研究从理论上解决了许多复杂的系统控制问题, 但是随着发展,实际生产系统的规模越来越大,控制对象、控制器、控制任务和LI的也更为复杂,导致现代控制理论的成果并未有在实际中很好的应用。

控制理论与控制系统的发展历史及趋势控制论一词Cybernetics,来自希腊语,原意为掌舵术,包含了调节、操纵、管理、指挥、监督等多方面的涵义。
因此“控制”这一概念本身即反映了人们对征服自然与外在的渴望,控制理论与技术也自然而然地在人们认识自然与改造自然的历史中发展起来。
根据控制理论的理论基础及所能解决的问题的难易程度,我们把控制理论大体的分为了三个不同的阶段。
这种阶段性的发展过程是由简单到复杂、由量变到质变的辩证发展过程。
一、经典控制论阶段(20世纪50年代末期以前)经典控制理论,是以传递函数为基础,在频率域对单输入---单输入控制系统进行分析与设计的理论。
1、控制系统的特点单输入---单输出系统的,线性定常或非线性系统中的相平面法也只含两个变量的系统。
2、控制思路基于频率域内传递函数的“反馈”和“前馈”控制思想,运用频率特性分析法、根轨迹分析法、描述函数法、相平面法、波波夫法,解决稳定性问题。
3、发展事件回顾1)我国古人发明的指南车就应用了反馈的原理2)1788年J.Watt在发明蒸汽机的同时应用了反馈思想设计了离心式飞摆控速器,这是第一个反馈系统的方案。
3)1868年J.C.Maxwell为解决离心式飞摆控速器控制精度和稳定性之间的矛盾,发表《论调速器》,提出了用基本系统的微分方正模型分析反馈系统的数学方法。
4)1868年,韦士乃格瑞斯克阐述了调节器的数学理论。
5)1875年E.J.Routh和A.Hurwitz提出了根据代数方程的系数判断线性系统稳定性方法6)1876年俄国学者N.A.维什涅格拉诺基发表著作《论调速器的一般理论》,对调速器系统进行了全面的理论阐述。
7)1895年劳斯与古尔维茨分别提出了基于特征特征根和行列式的稳定性代数判别方法。
8)1927年H.S.Black发现了采用负反馈线路的放大器,引入负反馈后,放大器系统对扰动和放大器增益变化的敏感性大为降低。
9)1932年H.Nyquest采用频率特性表示系统,提出了频域稳定性判据,很好地解决了Black 放大器的稳定性问题,而且可以分析系统的稳定裕度,奠定了频域法分析与综合的基础。
绪论0.1控制理论产生及发展18世纪中叶英国第一次工业革命1765年瓦特发明蒸汽机→调速问题→稳定性问题1868年调节器一文发表1872年劳斯和1890年赫尔威茨→代数判据1892年李雅普诺夫“运动稳定性的一般问题”1932年乃奎斯特判据1948 维纳发表《控制论—或关于在动物和机器中控制和通讯的科学》0.2 控制理论发展三个阶段:第一代:古典控制理论(经典控制理论)40-60年代第二代:现代控制理论60-80年代第三代:智能控制及大系统理论80-至今三代控制理论对比简表0.3 智能控制的产生及发展20世纪60年代 Smith 用模式识别器用于最优控制1965年 Zadeh 发表模糊集合论文,付京孙讲人工智能用于学习控制 1976年 Mendel 提出人工智能概念—智能控制70年代初 傅京孙、Gloriso 和Saridis 等人提出递阶智能控制的系统结构 1974年 马丹尼提出世界上第一个模糊控制器(fuzzy logic controller) 20世纪80年代初 建立了多种专家系统20世纪80年代中后期 神经网络的研究又开始兴起 1992年 美国自然基金启动支持“智能控制”的研究0.4 传统控制与智能控制结论:智能控制理论是对传统控制理论的发展,传统控制理论是智能控制理论的低级阶段。
0.5 智能控制论控制三要素: 信息—反馈—控制 智能控制——智能信息反馈控制图0.1 反馈控制系统的原理框图0.6思维科学与智能模拟1. 什么是思维科学研究思维规律和方法的科学。
思维是意识的一部分,而且是最重要的部分,思维是人脑对客观事物间接的反映过程,包括回想、联想、想像、思考、推想等。
人们通过思维活动反映客观事物的特点、本质属性、内部联系及发展规律。
因此思维是人们认识过程的高级阶段。
2.思维的类型(1) 抽象思维(逻辑思维):抽去表象的思维,例如小学生的算数。
(2)形象思维(直觉思维):既看形又看象的思维。
《现代控制系统》
【原创版】
目录
1.控制系统的基本概念
2.现代控制系统的发展历程
3.现代控制系统的核心技术
4.现代控制系统的应用领域
5.我国现代控制系统的发展现状与挑战
正文
一、控制系统的基本概念
现代控制系统是工程技术领域的一个重要分支,主要研究在不确定性环境下,如何通过各种控制方法和技术实现对被控对象的有效控制。
控制系统的基本概念包括控制对象、控制器、控制量和被控变量等。
二、现代控制系统的发展历程
现代控制系统的发展可以分为三个阶段:经典控制理论阶段、现代控制理论阶段和智能控制阶段。
经典控制理论阶段主要研究线性时不变系统的稳定性和鲁棒性;现代控制理论阶段则涉及到非线性、时变和分布式系统的控制问题;智能控制阶段则利用人工智能、神经网络和模糊控制等技术解决复杂系统的控制问题。
三、现代控制系统的核心技术
现代控制系统的核心技术包括:模型预测控制、自适应控制、神经网络控制、模糊控制、智能优化算法等。
这些技术在工业过程控制、航天器控制、汽车电子控制等领域得到了广泛应用。
四、现代控制系统的应用领域
现代控制系统在许多领域都发挥着重要作用,如工业过程控制、电力系统控制、交通运输系统控制、自动化制造、机器人控制等。
在这些领域,现代控制系统技术可以提高系统的性能、稳定性和可靠性,从而提高生产效率和产品质量。
五、我国现代控制系统的发展现状与挑战
我国现代控制系统在理论研究和应用方面取得了显著的成果,但在技术水平、创新能力和产业化方面与发达国家相比还存在一定差距。
自动控制理论是一门研究如何设计稳定、鲁棒和高性能控制系统的学科。
自动控制理论的发展可以分为以下几个阶段:
1. 经典控制理论阶段:20世纪前半叶,经典控制理论主要集中在线性系统的研究上,包括PID控制器、根轨迹法、频域分析等方法。
这些方法主要适用于线性、稳定、可预测的系统。
2. 现代控制理论阶段:20世纪60年代后期至70年代初期,现代控制理论开始崭露头角,状态空间方法、最优控制理论、鲁棒控制理论等相继涌现,为非线性、时变系统的分析与设计提供了新的思路。
3. 数字控制理论阶段:随着计算机技术的发展,数字控制理论应运而生。
数字信号处理技术的应用使得控制系统设计更加灵活,同时也促进了实时控制的发展。
4. 智能控制理论阶段:近年来,随着人工智能和机器学习的快速发展,智能控制理论逐渐引起关注。
模糊控制、神经网络控制、遗传算法等方法被引入到控制领域,为复杂系统的建模与控制提供了新的思路。
5. 网络化控制理论阶段:随着物联网和云计算技术的快速发展,网络化控制理论成为一个新的研究热点。
研究者们开始探索在网络环境
下的控制系统设计与实现,涉及到网络延迟、数据丢失、安全性等问题。
总的来说,自动控制理论的发展经历了经典理论、现代理论、数字化、智能化和网络化等多个阶段,不断地推动着控制理论与技术的进步,为各种工程和科学应用提供了强大支持。
经典控制理论是以传递函数为基础的一种控制理论,控制系统的分析与设计是建立在某种近似的和(或)试探的基础上的、控制对象一般是单输入单输出、线性定常系统;对多输入多输出系统、时变系统、非线性系统等.则无能为力。
经典抑制理论主要的分析方法有频率特性分析法、根轨迹分析法、描述函数法、相平面法、波波夫法等。
控制策略仅局限于反馈控制、PID控制等。
这种控制不能实现最优控制。
现代控制理论是建立在状态空间上的一种分析方法,它的数学模型主要是状态方程,控制系统的分析与设计是精确的。
控制对象可以是单输入单输出控制系统.也可以是多输人多输出控制系统,可以是线件定常控制系统,也可以是非线性时变控制系统,可以是连续控制系统,也可以是离散和(或)数字控制系统。
因此,现代控制理论的应用范围更加广泛。
主要的控制策略有极点配置、状态反馈、输出反馈等。
由于现代控制理论的分析与设计方法的精确性,因此,现代控制可以得到最优控制。
但这些控制策略大多是建立在已知系统的基础之上的。
严格来说.大部分的控制系统是一个完全未知或部分未知系统,这里包括系统本身参数未知、系统状态未知两个方面,同时被控制对象还受外界干扰、环境变化等的因素影响。
您现在所阅读的文章来源于第一机电网
智能控制是一种能更好地模仿人类智能的、非传统的控制方法,它采用的理论方法则主要来自自动控制理论、人工智能和运筹学等学科分支。
内容包括最优控制、自适应控制、鲁棒控制、神经网络控制、模糊控制、仿人控制等。
其控制对象可以是已知系统也可以是未知系统,大多数的控制策略不仅能抑制外界干扰、环境变化、参数变化的影响,还能有效地消除模型化误差的影响。
1/ 1。