电磁振荡电路

第1节电磁振荡课标解读课标要求素养要求1.知道LC振荡电路的组成及振荡过程中电感线圈和电容器的作用。

2.了解LC振荡电路中各物理量的变化规律。

3.知道影响LC振荡电路的振荡周期(频率)的有关因素并会进行简单计算。

1.物理观念:理解电场能、磁场能在相互转化过程中的能量守恒观，体会i与磁场、q与电场的因果观。

2.科学探究:探究电磁振荡中q、i、E、B、电场能、磁场能之间的关系。

3.科学思维:用类比的思想对电磁振荡与机械振动进行对比，通过揭示相关量深入理解电磁振荡。

4.科学态度与责任:培养学生实事求是的科学态度。

自主学习·必备知识教材研习教材原句要点一振荡电流电路的电压发生周期性的变化，电路中的电流也发生周期性的变化。

像这样大小和方向都做周期性迅速①变化的电流，叫作振荡电流。

要点二电磁振荡的周期和频率电磁②振荡完成一次周期性变化需要的时间叫作周期。

电磁振荡完成周期性变化的次数与所用时间之比叫作它的频率，数值等于单位时间内完成的周期性变化③的次数。

要点三电磁振荡中的能量损失如果没有能量损耗，振荡可以永远持续下去，振荡电流的振幅保持不变④。

但是，任何电路都有电阻，电路中总会有一部分能量会转化为内能。

另外，还会有一部分能量以电磁波的形式辐射出去。

这样，振荡电路中的能量就会逐渐减少，振荡电流的振幅也就逐渐减小⑤，直到最后停止振荡。

自主思考①如何理解振荡电流的“迅速”变化？答案：提示振荡电流实际上就是交变电流，由于变得快，所以指“频率较高”的交变电流。

②如何理解电磁振荡的“电”和“磁”?答案：提示电磁振荡中的“电”不仅指电容器两极板上的电荷量q，也指该电荷产生的电场，包括电场强度E、电势差U、电场能E电，“磁”不仅指线圈中的电流i，也指该电流产生的磁场，包括磁感应强度B、磁场能E磁，电磁振荡是指电荷量、电场、电流、磁场都随时间做周期性变化的一种现象。

③什么是电磁振荡的“周期性变化”？答案：提示LC振荡电路中的电流i、线圈里的磁感应强度B、电容器极板上的电荷量、电容器里的电场强度等各物理量所进行的一个相同的重复性变化的现象。

LC 回路中电磁振荡的规律及周期和频率Wangqixue@ 邮编222100由自感线圈L 和电容器C 组成的电路，称为LC 回路，又称振荡电路．在LC 回路中，通过电容器的充电和放电及振荡线圈阻碍电流变化的作用，线圈中形成了周期性变化的振荡电流，电容器极板间形成了周期性变化的电荷，与电荷、电流对应的电场及磁场也做周期性变化．这种现象叫做电磁振荡．一、LC 回路的电磁振荡规律1.电荷q 、电流i 随时间t 的变化规律及两者之间的关系图1甲是电容器极板上电荷q 随时间t 做周期性变化的情况．图1乙是线圈中的电流i 随时间t 做周期性变化的情况，若电荷q 是按余弦(或正弦)规律变化的．电流i 则按正弦（或余弦）规律变化．二者之间是互余的的关系（如图1所示）．— 因回路中的电荷一定，故当电容器极板上“聚集”电荷最多时，线圈中“流过”的电荷为零――电流为零，即max q q 0i ==时，；当电容器极板上“聚集”电荷减少（放电）时，线圈中“流过”的电荷增多――电流增大，即q ↓i ⇒↑；反之，当电容器极板上“聚集”电荷最少时，线圈中“流过”的电荷最多――电流最大．m ax q 0i i ==即时,；而当电容器极板上“聚集”的电荷增多（充电）时，线圈中“流过”的电荷减少――电流减小，即q ↑i ⇒↓． 2.电场能与磁场能的变化关系电磁振荡的过程实质上是电容器中的电场能和自感线圈中的磁场能相互转化的过程，若LC 回路中没有能量损失，在能量相互转化时，保持守恒．磁场能最弱时电场能最强，反之亦然．而且，电容器上的电荷q 、电压u 、两极板间的场强及电场能的变化步调一致，同增同减，同时达到最大或同时为零．而线圈中的电流i 、磁感应强度B 及磁场能的变化步调一致，同增同减，同时达到最大或同时为零．例1.LC 回路电容器两端的电压u 随时间t 变化的关系如图2所示，则（ ） A. 在时刻t 1，电路中的 电流最大B. 在时刻t 2 ，电路中的磁场能最大C. 从时刻t 2至 t 3，电路中的电场能不断增大D. 从时刻t 3 至t 4，电容器的带电量不断增多解析：由LC 回路电磁振荡规律及图示可知，t 1时刻电容器两端电压u 最高⇒电容器极板上所带电量q 最大⇒电路中振荡电流i 最小；在t 2时刻电容器极板上两端电压u 为零⇒电容器极板上所带电量q 为零⇒电路中振荡电流i 最强⇒电路中的磁场能最大；在t 2至 t 3过程中，电容器两极板间电压u 在增大⇒电容器极板上所图1甲乙图2带电量q 在增多⇒电场能不断增大；在 t 3 至t 4的过程中，电容器两极板间电压u 在减小⇒电容器极板上所带电量q 在减小．正确选项为B 、C评注：这类问题应根据电荷与电流之间的变化关系判断．当max q q 0;i ==时，且 q ↓i ⇒↑；电容器上的电压u 、两极板间的场强及电场能与电荷q 变化步调一致．反之．当m ax q 0i i ==时；且 q ↑i ⇒↓，而线圈中磁感应强度B 及磁场能与电流i 的变化步调一致． 例2．某时刻LCA. 振荡电流i 在减小B. 振荡电流i 在增大C. 电场能正在向磁场能变化D. 磁场能正在向电场能变化解析：由图3中上极板带正电荷下极板带负电荷荷及电流的方向可判断出正电荷在向正极板聚集，说明电容器极板上电荷在增加，电容器正在充电．电容器充电的过程中电流减小，磁场能向电场能转化．正确选项为A 、D ．评注：要判断电流是在增大还是在减小，可先判断出电容器是在充电还是在放电，而判断电容器是在充电还是在放电，不能单纯地由电流的方向决定，还应结合电容器两极板上电荷的分布情况．若图中电流的方向不变，而上极板带负电荷下极板带正电荷，则电容器是在放电（正、负电荷相互中和）例3.LC 振荡电路中，某时刻磁场方向如图4所示，则下列说法中错误的是（ ） A. 若磁场正在减弱，则电容器上极板带正电 B. 若电容器正在放电，则电容器上极板带负电C. 若电容器上极板带正电，则线圈中电流正在增大D.若电容器正在放电，则自感电动势正在阻碍电流增大解析：由电流的磁场方向根据安培定则可判断出振荡电流在 回路中为顺时针方向，由于电容器极板的带电情况未知，必须 设出电容器带电的两种情况并结合电流的变化情况综合进行讨论．若该时刻电容器上极板带正电，则电容器在充电，电流减小，磁场减弱；若该时刻电容器上极板带负电，则电容器在放电；若电容器正在放电，则电荷减小，电流增大，由愣次定律知自感电动势阻碍电流增大．错误选项为C ．评注：该题考查了安培定则、电磁振荡的规律及愣次定律，且电容器极板的带电情况未标明，故该题具有一定难度．例4.如图5所示电路中，L 是电阻不计的线圈，C 为电容器，R 为电阻，开关S 先是闭合的，现将开关S 断开，并从这一时刻开始计时，设电容器A 极板带正电时电荷为正，则电容器A 极板上的电荷q 随时间t 变化的图像是图6中的哪一个（ ）Ci图3A BL C S R图5 图4解析：开关S 闭合时，线圈中有自左向右的电流通过，由于线圈的电阻为零，线圈及电容器两端的电压为零．LC 回路的起始条件是线圈中电流最大，磁场能最大，电容器两极板的电荷为零，电场能为零．断开开关S 时，线圈中产生与电流方向相同的自感电动势，阻碍线圈中电流的减小，使LC 回路中电流方向沿瞬时针方向流动，从而对电容器充电，B 板带正电，A 板带负电，电荷逐渐增加，经4T 电量达最大，这时LC 回路中电流为零，由此可推知，电容器A 极板上的电荷q 随时间t 变化的图像是B 图．答案为B评注：该题中LC 回路产生电磁振荡的初始条件是线圈中电流最大，磁场能最大，电容器两极板的电荷为零，电场能为零．这种方式是先给回路提供磁场能．如果LC 回路的初始条件为电容器极板上的电量最大，而线圈中的电流为零，则电场能最大，磁场能为零．这种方式是先给回路提供电场能．二、电磁振荡的周期和频率电磁振荡完成一次周期性变化需要的时间叫做周期．一秒钟内完成的周期性变化的次数叫频率．如果没有能量损失，也不受其他外界的影响，这时电磁振荡的周期和频率叫做振荡电路的固有周期和固有频率．简称振荡电路的周期和频率．其公式分别为：T=2πf =两者之间是互为倒数的关系，即T=1f例5.LC 振荡电路的固有频率为f ，则（ ） A. 电容器内电场变化的频率为f B. 电容器内电场变化的频率为2f C. 电场能和磁场能转化的频率为f D. 电场能和磁场能转化的频率为2f解析：电场能和磁场能是标量，只有大小在做周期性变化．所以电场能和磁场能转化的周期是电磁振荡周期的一半，转化的频率为电磁振荡频率的两倍．而电容器内电场变化ABCD图6的频率等于电磁振荡的频率．正确选项为A 、D ．评注：LC 回路中的振荡电流、电压、电场强度、磁感应强度的方向和电容器极板上电荷的电性在电磁振荡的一个周期内改变两次．它们的频率与电磁振荡的固有频率相同．例6.如图7所示，LC 回路中振荡电流的周期为2×10-2s ，自振荡电流沿逆时针方向达最大值时开始计时，当t ＝3.4×10-2s 时，电容器正处于_______状态（填“充电”、“放电”、“充电完毕”或“放电完毕”）．这时电容器的上极板________(填“带正电”、“带负电”或“不带电”)． 解析：设t=3.4×10-2s ＝2×10-2s ＋1.4×10-2s ＝T+t ′， 则2T ＜t ′＜34T ，且t 时刻和t ′时刻电路的振荡状态相同．做出振荡电流i －t 图象如图8，可知在2T ～34T 时间内，电流减小，电容器所带电荷增加，电容器处于充电状态，此时电流方向为顺时针方向，可判断出电容器的上极板带正电．答案：充电、带正电评注：根据电磁振荡具有周期性特点，在分析t ＞T 时刻的振荡情况时，可由变换式t ＝nT+ t ′求得t ′（n 为正整数，0＜t ′＜T ），再分析t ′时刻的振荡状态．L C 图7－图8。

第1节 电磁振荡[学习目标要求] 1.知道什么是振荡电流和振荡电路。

2.知道LC 振荡电路中振荡电流的产生过程，知道电磁振荡过程中能量转化情况。

3.知道电磁振荡的周期和频率，知道LC 电路的周期和频率与哪些因素有关，并会进行相关的计算。

一、电磁振荡的产生1．要产生持续变化的电流，可以通过线圈和电容器组成的电路实现。

2．振荡电流：大小和方向都做周期性迅速变化的电流。

3．振荡电路：产生振荡电流的电路。

4．LC 振荡电路：由电感线圈L 和电容C 组成的电路就是最简单的振荡电路。

5．电磁振荡：在整个过程中，电路中的电流i 、电容器极板上的电荷量q 、电容器里的电场强度E 、线圈里的磁感应强度B ，都在周期地变化，这种现象就是电磁振荡。

二、电磁振荡中的能量变化 1．能量变化过程(1)电容器刚放电时：电场最强，电场能最大。

(2)开始放电后：电场能――→转化磁场能。

(3)放电完毕：电场能为零，磁场能最大。

(4)反向充电：磁场能――→转化电场能。

(5)反向充电完毕：电场能最大。

2．等幅振荡振荡电路的能量会逐渐减小，适时地把能量补充到振荡电路中就可以得到振幅不变的等幅振荡。

【判一判】(1)LC振荡电路的电容器放电完毕时，回路中磁场能最小。

(×)(2)LC振荡电路的电容器极板上电荷量最多时，电场能最大。

(√)(3)LC振荡电路中电流增大时，电容器上的电荷一定减少。

(√)(4)LC振荡电路的电流为零时，线圈中的自感电动势最大。

(√)三、电磁振荡的周期和频率1．周期：电磁振荡完成一次周期性变化需要的时间。

LC振荡电路的周期公式T ＝2πLC。

2．频率：电磁振荡完成周期性变化的次数与所用时间之比叫作它的频率。

数值上等于单位时间内完成的周期性变化的次数。

LC振荡电路的频率公式f＝1，式中T、f、L、C的单位分别是秒(s)、赫兹(Hz)、亨利(H)、法拉(F)。

2πLC【判一判】(1)在振荡电路中，电容器充电完毕的瞬间磁场能全部转化为电场能。

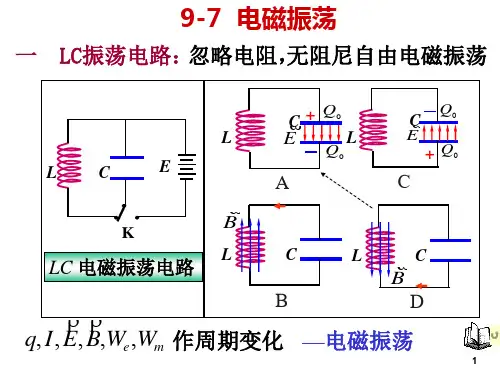
振荡电路原理振荡电路是一种能够产生连续交变信号的电路，它是电子设备中非常重要的一部分。

在许多应用中，振荡电路被广泛用于产生稳定的频率信号，例如在无线通信、音频设备、计算机等领域。

振荡电路的工作原理是基于正反馈的原理，通过将一部分输出信号反馈到输入端，使得系统产生自激振荡的现象。

振荡电路的核心是谐振电路，它由一个能够存储能量的电感和一个能够存储能量的电容组成。

当电路中的电容充电时，电感中产生磁场，接着电容放电，磁场崩塌，产生电流，使得电容再次充电，如此往复，形成电路的振荡。

振荡电路可以分为LC振荡电路、RC振荡电路和RLC振荡电路等不同类型。

LC振荡电路是最简单的一种振荡电路，由电感和电容构成。

在LC 振荡电路中，当电路中的电容充电至某一电压时，电感中储存的能量开始释放，导致电容器电压降低，最终电容放电完毕后，电感中的能量被转化为电容器的电荷，电路重新开始充电。

这种过程不断重复，从而产生稳定的振荡信号。

RC振荡电路是由电阻和电容构成的振荡电路。

在RC振荡电路中，电容器通过电阻放电，电压下降，直到最终电容器放电完毕。

在这一过程中，电阻消耗了电容器储存的能量，而电容器重新开始充电，这一过程循环进行，形成振荡。

RLC振荡电路则是由电阻、电感和电容器构成的振荡电路。

在RLC 振荡电路中，电容器和电感之间的能量转换导致振荡的产生。

当电容充电时，电感中储存能量，最终电容放电完毕后，电感释放能量，使得电容重新开始充电，循环往复，产生振荡。

总的来说，振荡电路的原理是基于谐振电路的工作原理，通过正反馈的机制使电路产生自激振荡，产生稳定的交变信号。

不同类型的振荡电路在实际应用中有着各自的特点和优势，可以根据具体的需求选择适合的振荡电路。

振荡电路在电子领域中有着广泛的应用，是现代电子设备中不可或缺的部分。