直线与平面平行的性质ppt课件

AD
AE AF
上的点，若 EB ，FD则EF与平面BCD的位置关系是
_E_F_/_/_平_面__B_C_D____.
利用平行线定理 证线线平行.
A F
E D
B
C
2.如图，四棱锥A-DBCE中，O为底面
正方形DBCE对角线的交点，F为AE的
中点. 求证: AB//平面DCF.
分析: 连结OF.
A F
一、知识回顾：
空间中直线与平面有几种位置关系？
a
直线在平面内 α
有无数个公共点
直线与平面相交 α
a
.P 有且只有一个公共点
a 直线与平面平行
α
没有公共点
二、引入新课
怎样判定直线与平面平行呢？
a
三、实例感受
在门扇的旋转过程中: 直线AB在门框所在的平面外 直线CD在门框所在的平面内 直线AB与CD始终是平行的
因为E，F分别是AB，
E
F D
C
B
AD 的中点,所以EF//BD
因为 EF 平面BCD, BD 平面BCD
由直线与平面平行的判断定理得:
EF//平面BCD.
小结：在平面内找(作)一条直线与平面外的直线平行时可以通过 三角形的中位线、梯形的中位线、平行线的性质等来完成。
变式练习
1. 如图，在空间四边形ABCD中，E、F 分别为AB、
AD的中点.
∴EH∥BD且EH= 1 BD
同理GF
2
∥BD且GF=
1 2
BD
EH ∥GF且EH＝GF
H E
D
B
G
∴E、F、G、H四点共面。
F C
（2） AC ∥平面EFGH

1
∴AM＝2DC，AM∥DC，
∴AM∥GN，AM＝GN，∴四边形AMNG为平行四边形，
∴MN∥平面PAD.
∴MN∥AG.又MN⊄平面PAD，AG⊂平面PAD，
课堂小结
1.直线与平面平行的判定定理
线线平行
线面平行
如果平面外一条直线与此平面内的一条直线平行，那么该直线与
此平面平行.
2.直线与平面平行的性质定理
基本事实4 平行于同一条直线的两条直线平行.
3、等角定理
定理 如果空间中两个角的两边分别对应平行，那么这两个角相等或互补.
复习回顾
4、直线与平面有哪些位置关系？
(1)直线在平面内——有无数个公共点；
⊂
(2)直线与平面相交——有且只有一个公共点； ∩ =
直线在平面外
(3)直线与平面平行——没有公共点.
线线平行Βιβλιοθήκη 线面平行一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么
该直线与交线平行.
3．应用线面平行的判定定理证明线面平行的基本步骤：
（1）利用性质定理在面内找平行线;
（2）证明直线与直线平行；
（3）说明两线与平面的位置关系（一条在面内，一条不在面内）；
（4）得出结论.
E
证明： 连接BD.
F
∵ AE EB,AF FD,
∴ EF / / BD.
又 EF 平面BCD,BD 平面BCD,
D
B
C
∴ EF / / 平面BCD.
今后要证明一条直线与一个平面平行，只要在这个平面内找出一
条与此直线平行的直线就可以了.
巩固训练
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，

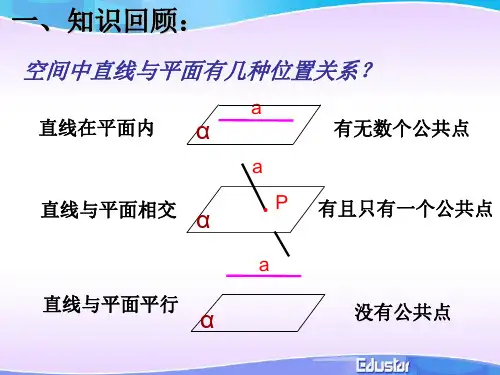
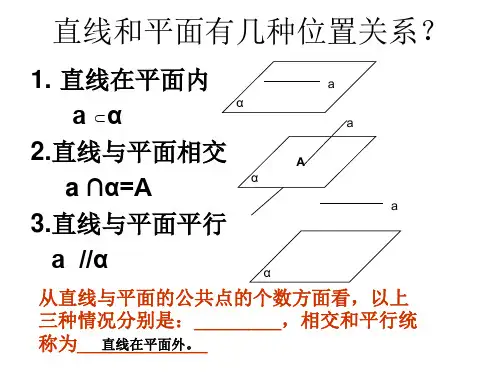
【解析】选A.对于①，若a∥b,bα, 则应有a∥α或aα,所以①不正确; 对于②，若a∥平面α，bα,则应有a∥b或a与b异面，故② 不正确; 对于③，若a∥b,a∥α,则应有b∥α或bα,因此③也不正 确； 对于④，若a∥α,b∥α,则应有a∥b或a与b相交或a与b异面，
因此④是错误的.
9.(10分)如图，已知，四棱锥A—BCDE中，M为AB中点，底面
BCDE为梯形，其中CD∥BE，试判断直线EM是否平行于平面ACD，
并说明理由.Biblioteka 【解析】EM与平面ACD不平行.
理由：假设EM∥平面ACD.
∵BE∥CD,CD 平面ACD，BE 平面ACD.
∴BE∥平面ACD.
又∵BE∩EM=E.∴平面AEB∥平面ACD. 而A∈平面AEB，A∈平面ACD.与平面AEB∥平面ACD矛盾. ∴假设不成立，∴EM与平面ACD不平行.
4.如图，四棱锥S-ABCD的所有的
棱长都等于2,E是SA的中点，过 C,D,E三点的平面与SB交于点F,
则四边形DEFC的周长为(
(A)2+ 3 (C)3+2 3
)
(B)3+ 3 (D)2+2 3
【解析提示】先证明EF∥AB，再根据三角形中位线等知识求
解.
【解析】选C.∵AB=BC=CD=AD=2， ∴四边形ABCD为菱形，∴CD∥AB. 又CD 平面SAB,AB 平面SAB∴CD∥平面SAB. 又CD 平面CDEF,平面CDEF∩平面SAB=直线EF ∴CD∥EF.∴EF∥AB.
【证明】连接A1C交AC1于点E，连接DE.
∵A1B∥平面AC1D. A1B 平面A1BC.平面A1BC∩平面AC1D=DE. ∴A1B∥DE, 又四边形ACC1A1为平行四边形.∴E为A1C中点.

本题的核心条件，特殊的位置关系，必有点 F 特殊的数量关系．
(1)求证：EF∥平面 ADO； (2)若∠POF＝120°，求三棱锥 P-ABC 的体积．此条件暗示 △POF 的特殊性，即平面 POF⊥平面 ABC.
高考一轮总复习•数学
第18页
(1)证明：如图，连接 DE.设 AF＝tAC，t∈[0,1]，则B→F＝B→A＋A→F＝(1－t)B→A＋tB→C，A→O＝ －B→A＋12B→C.由 BF⊥AO，AB⊥BC，
第25页
高考一轮总复习•数学
∵∠DAB＝120°，AD＝AB， ∴∠ADB＝∠ABD＝30°，∠ADC＝∠CDB＋∠ADB＝60°＋30°＝90°， ∴AD⊥CD，∴MB∥AD. 又 MB⊄平面 PAD，AD⊂平面 PAD， ∴MB∥平面 PAD. ∵EM∩MB＝M，EM，MB⊂平面 EMB， ∴平面 EMB∥平面 PAD，∵EB⊂平面 EMB，∴EB∥平面 PAD.
高考一轮总复习•数学
第28页
题型
面面平行的判定与性质
典例 2(2024·四川绵阳中学月考)如图，在三棱柱 ABC-A1B1C1 中，E，F，G，H 分别是 AB，AC，A1B1，A1C1 的中点．求证：
(1)B，C，H，G 四点共面； (2)平面 EFA1∥平面 BCHG. 思考判定定理，即需要两组平行线的关系．
高考一轮总复习•数学
第32页
对点练 2(2024·四川达州一诊)如图所示，设正方体 ABCD-A1B1C1D1 的棱长为 a，P 是 棱 AD 上一点，且 AP＝a3，过 B1，D1，P 的平面交平面 ABCD 于 PQ，Q 在直线 CD 上，则 PQ＝( )
A.2 3 2a B. 3 2a C. 2 2a D.2 3 3a

的稳定性和美观性。
02
建筑测量
在建筑测量中，直线与平面平行的概念对于确定建筑物是否垂直和水平
非常重要。测量师使用铅锤和水平仪等工具来确保建筑物的基础、柱子
和横梁等结构与地面平行。
03
建筑结构分析
在建筑结构分析中，直线与平面平行的概念对于评估结构的稳定性和安
全性至关重要。工程师使用这些概念来分析建筑物的支撑结构和受力情
电子设备制造
在电子设备制造中，直线与平面平行的概念对于确保电子设备的精确度和质量非常重要。制造商使用这些概念来控制 装配和焊接过程，以确保电子元件的放置和连接正确。
电子设备维修
在电子设备维修中，直线与平面平行的概念对于检查和调整电子元件的位置非常重要。维修人员使用这 些概念来检查设备的平行度和垂直度，以确保设备的正常运行和性能。
文字描述
如果一条直线与一个平面平行， 那么这条直线与此平面内的任何 直线都平行。
解释
这个定理说明了直线与平面平行 的条件，即直线必须与平面内的 所有直线都平行，才能判定该直 线与该平面平行。
直线与平面平行判定定理的数学公式
数学公式
若直线$l$与平面$alpha$平行，则对于任意直线$m$在平面$alpha$上，都有 $l parallel m$。
02
若直线$l$与平面$alpha$平行， 则对于任意点$P$在平面$alpha$ 上，有$l cap P = emptyset$。
直线与平面平行性质定理的图形解释
当直线与平面平行时，该直线与平面 内的所有直线都保持平行关系，没有 交点。
在图形中，可以标出一些具体的点来 解释该性质定理，例如选择平面上的 一些点并观察它们是否与直线有交点 。
可以通过作一条与已知直线平行的直 线来验证该性质定理，观察新作的直 线是否与平面内的其他直线平行且无 交点。

A
平面CC’D’D 答：1）平面 ）平面A’B’C’D’, 平面 答：2）平面 ）平面A’B’C’D’，平面 ，平面ADD’A’
答：3）平面 ）平面ADD’A’
问问1 问问2 问问3
D' B'
M D N
C'
若 M， N分 分 ， 分 为 D'A，D'B的 ， 的 中 中 ， 则 MN 与 平 平_____ 平 平？
如何判断直线与平面平行？ 如何判断直线与平面平行？
• 思考1：请大家利用手中的模型， 思考1 请大家利用手中的模型， 看看有哪些直线与平面是平行的， 看看有哪些直线与平面是平行的， 理由又是什么？ 理由又是什么？
如何判断直线与平面平行？ 如何判断直线与平面平行？
• 思考2：观察门扇转动，或者翻动 思考2 观察门扇转动， 书的封面这一运动变化过程中， 书的封面这一运动变化过程中，有 没有某些直线与某些平面平行？ 没有某些直线与某些平面平行？为 什么？ 什么？ • 观察演示，想想在转动过程中，橡 观察演示，想想在转动过程中， 皮筋所在的直线与底面是否平行？ 皮筋所在的直线与底面是否平行？ 如何摆就能使它们平行？ 如何摆就能使它们平行？
• 例1、求证：空间四边形相邻两 、求证： 边中点的连线平行于经过另外 两边所在的平面。 两边所在的平面。
A E B C F D
例2：P是平行四边形ABCD所在平面外 是平行四边形ABCD所在平面外 ABCD 一点， PA的中点 求证：PC//平 的中点， 一点，Q是PA的中点，求证：PC//平 面BDQ.
如何判断直线与平面平行？ 如何判断直线与平面平行？
a
• 思考4： 思考4 如果平面外 b α 的一条直线a 的一条直线a与 平面内的直线b 平面内的直线b 平行，那么a 平行，那么a平行于平面α吗？

判定定理二：向量
03
共线法
向量共线法原理
定义
若两向量方向相同或相反，则称这两 向量共线。
性质
应用
在直线与平面平行判定中，通过判断 直线的方向向量与平面上两不共线向 量的关系，确定直线与平面的位置关 系。
共线的向量可以表示为同一基向量的 倍数。
向量运算规则
加法运算
向量加法满足平行四边形 法则或三角形法则。
$l parallel alpha$。
实例二
若直线$l$的方向向量$vec{a}$ 与平面$alpha$的法向量
$vec{n}$满足$vec{a} cdot vec{n} = 0$，则$l parallel
alpha$。
讨论
通过实例分析，我们可以发现向 量共线法在直线与平面平行判定 中的重要作用。同时，需要注意 判定条件的充分性和必要性，以
及特殊情况的处理。
判定定理三：距离
04
相等法
距离相等法原理
直线与平面平行时，直线上任意一点 到平面的距离都相等。
利用这一性质，可以通过比较直线上 不同点到平面的距离是否相等来判断 直线与平面是否平行。
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距 离公式为
直线与平面的距离为零
当直线上的任意一点到平面的距离都为零时，直线与平面平行。可 以通过计算点到平面的距离公式来判断。
复杂问题简化策略
转化为基本问题
将复杂问题转化为判断直线与平面是否平行的基本问题，以便运 用上述方法进行求解。
利用已知条件
充分利用题目中给出$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$

A.1个
B.2个
C.3个
D.4个
D解析 由题图知正方体的前、后、左、右四个面都与EF平行.
高中数学 必修第二册 RJ·A
4.如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，
DA上的点(不与端点重合)，EH∥FG，则EH与BD的位置关系是
A.平行
B.相交
C.异面
D.不确定
A解析 ∵EH∥FG，EH⊄平面BDC，FG⊂平面BDC， ∴EH∥平面BDC， 又EH⊂平面ABD且平面ABD∩平面BDC＝BD， ∴EH∥BD.
高中数学 必修第二册 RJ·A
反思感悟
利用直线和平面平行的判定定理证明线面平行的关键是在平面内找一条直线与 已知直线平行，常利用平行四边形、三角形中位线、基本事实4等.
高中数学 必修第二册 RJ·A
跟踪训练
如图，四边形ABCD是平行四边形，P是平面ABCD外一点，M，N分 别是AB，PC的中点.求证：MN∥平面PAD.
所以 a∥EG，即 BD∥EG，所以AACF＝AAEB.
又EBGD＝AAEB，所以AACF＝EBGD， 于是 EG＝AFA·CBD＝55×＋44＝290.
高中数学 必修第二册 RJ·A
反思感悟
(1)利用线面平行的性质定理找线线平行，利用线线平行得对应线段成比例即 可求线段长度. (2)通过定理的运用和平行的性质，提升直观想象和逻辑推理素养.
高中数学 必修第二册 RJ·A
典例剖析
一、直线与平面平行的判定定理的应用
例1 如图，在正方体ABCD－A1B1C1D1中，E，F，G分别是BC，CC1，BB1的中点， 求证：EF∥平面AD1G.
高中数学 必修第二册 RJ·A

第八章 立体几何初步
第三节 直线、平面平行的判定与性质
栏目一 知识·分步落实 栏目二 考点·分类突破 栏目三 微专题系列
栏目导引
课程标准
考向预测
1.以立体几何的定义、公理和定理为
出发，借助长方体，通过直观感知， 考情分析： 直线与平面以及平面与
了解空间中线面平行的有关性质与 平面平行的判定和性质仍会是高考
所以 A1G 綊 EB，所以四边形 A1EBG 是平行四边形，
所以 A1E∥GB. 因为 A1E⊄平面 BCHG，GB⊂平面 BCHG， 所以 A1E∥平面 BCHG. 又因为 A1E∩EF＝E，所以平面 EFA1∥平面 BCHG.
1．如图，平面 α∥平面 β，△PAB 所在的平面与 α，β分别交于 CD，AB，
平行命题的判断 (1)解决与平行相关命题的判断问题，以与平行相关的判定定理和性质定 理为依据，注意定理中相关条件的检验，必须进行严密的逻辑推理． (2)如果判断某个命题错误，则往往利用正方体或其他几何体作为模型构 造反例说明．
直线与平面平行的判定与性质 角度一 直线与平面平行的判定
如图所示，斜三棱柱 ABC-A1B1C1 中，点 D，D1 分别为 AC，A1C1 的中点．求证：
BC∥平面ADF
BC⊂平面BCPQ
⇒BC∥PQ.
平面BCPQ∩平面ADF＝PQ
PQ∥BC
PQ⊄平面ABCD PQ∥平面 ABCD.
BC⊂平面ABCD
应用线面平行的性质定理的关键是确定交线的位置，有时 需要经过已知直线作辅助平面来确定交线．该定理的作用是由线面平行转化 为线线平行．
1．(2020·深圳市统一测试)如图，在直四棱柱 ABCD-A1B1C1D1 中，底面 ABCD 是平行四边形，点 M，

若两向量的点积为零，则 它们垂直。
应用
通过计算直线方向向量与 平面法向量的点积，可以 判断直线与平面是否平行 。
判定定理三：法向量垂直
定义
若一直线与一平面平行， 则该直线的法向量与该平 面的法向量平行。
推论
若两向量平行，则它们的 分量成比例。
应用
通过比较直线法向量与平 面法向量的分量比例，可 以判断直线与平面是否平 行。
直线与平面平行的定义
阐述直线与平面平行的基本概念，为后续判定定理 的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和 作用，以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理 及其证明方法，理解相关概念， 能够运用所学知识解决相关问题 。
100%
过程与方法
应用举例二：判断两平面是否平行
方法一
利用平行平面的性质，通过证明一个 平面内有两条相交直线分别与另一个 平面平行，从而判定两个平面平行。
方法二
利用向量法，通过计算两个平面的法 向量是否共线，从而判定两个平面是 否平行。
应用举例三：解决实际问题中的平行问题
1 2
实例一
在建筑设计中，利用直线与平面平行的性质，确 保建筑物的立面、地面等各部分保持平行，以达 到美观和稳定的效果。
定义
应用
若一直线与一平面平行，则该直线与 该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜 率，可以判断直线与平面是否平行。
推论
若两直线的斜率相等，则它们或者平 行或者重合。
判定定理二：方向向量平行
01
02
03
定义
若一直线与一平面平行， 则该直线的方向向量与该 平面的法向量垂直。