matlab画二元函数

精心整理Matlab基础练习题常量、变量、表达式1、MATLAB中，下面哪些变量名是合法的？（）2、3、4、5、）6、小数7、8、在MATLAB中，a=1，b=i，则a占_8__个字节，b占_16_个字节，c占________字节。

9、在MATLAB中，inf的含义是__无穷大__，nan的含义是__非数（结果不定）___。

数组1、在MATLAB中，X是一个一维数值数组，现在要把数组X中的所有元素按原来次序的逆序排列输出，应该使用下面的（）指令。

（A）X[end:1] （B）X[end:-1:1] （C）X(end:-1:1)（D）X(end:1) 2、在MATLAB中，A是一个字二维数组，要获取A的行数和列数，应该使用的MATLAB的命令是（）。

（A）class(A) （B）sizeof(A) （C）size(A)（D）isa(A)3、4、这5、6、___linspace(0,5,50)___7、在MATLAB中，A=[0:1/2:2]*pi，那么sin(A)=___[010-10]_____。

8、在MATLAB中，A=[1,2,3;4,5,6;7,8,0]，B=[2,1,6;8,5,2;14,2,1]。

写出下面MATLAB语句执行的结果：(为节省篇幅，把矩阵写成mat2str的形式)（1）A==B [000;010;000]（2）A.*B [2218;322512;98160]（3）A(:)' [147258360]（4）A(1,:)*B(:,3) 139、在MATLAB中，写出下面MATLAB语句执行的结果：（1）c lear,A=ones(2,6)A=（5）B=A（:,end:-1:1)B=211713951231915117310、请编写一段matlab程序，完成以下功能：（1） 生成一个100行，200列的二维随机数组；A=rand(100,200);（2） 找出数组A 中所有大于0.49且小于0.51的元素的单下标；Idx=find(A(:)>0.49&A(:)<0.51)（3） 数组A 中满足（2）中的条件的元素有多少个？11、12、 22cos 0.7sin (1)x y x x ⎡⎤=+⎢⎥+⎣⎦，编写一段matlab 程序，要求如下（1） 在[0,2]π区间，每隔0.01取一x 数值，计算出相应的y 的函数值；x=0:0.01:2*pi;y=(0.7+2*cos(x)./(1+x.^2)).*sin(x)（2）根据MATLAB计算出的数据，找出在[0,2]π内该函数的极小值的坐标。

梯度法是一种常见的数值优化方法，用于求解无约束优化问题。

以下是使用Matlab 梯度法求二元函数最小值的步骤：定义目标函数：首先需要定义要求解的目标函数。

比如对于一个二元函数f(x,y)，可以在Matlab 中定义为一个function handle 的形式：f = @(x) x(1)^2 + x(2)^2;计算梯度：使用gradient 函数计算目标函数的梯度，得到每个变量的偏导数。

例如，在Matlab 中可以这样计算f(x,y) 的梯度：grad = @(x) [2*x(1), 2*x(2)];初始化参数：确定起始点，即需要进行优化的初始值，例如：x0 = [1; 2];设置迭代次数和步长：根据实际情况，设置迭代次数和步长，例如：max_iter = 1000;alpha = 0.01;进行迭代：使用for 循环进行多次迭代，每次沿着梯度方向更新参数值，直至达到最小值或者迭代次数满足停止条件。

具体来说，可以实现如下代码：for i = 1:max_iterx1 = x0 - alpha*grad(x0);if abs(f(x1)-f(x0)) < 1e-6break;endx0 = x1;end其中，1e-6 表示允许的最小误差值。

输出结果：经过多次迭代之后，x0 中存储的即为所求的最小值点。

可以使用fprintf 函数将其输出：fprintf('The minimum point is (%f, %f)\n', x0(1), x0(2));这样就完成了在Matlab 中使用梯度法求解二元函数最小值的过程。

需要注意的是，在实际应用中，需要根据具体问题和实验数据调整步长和迭代次数等参数，以获得更好的优化效果。

matlab二元函数已知函数值求自变量MATLAB是一种常用的数学软件，可以用于解决各种数学问题，包括求解二元函数。

在本文中，我们将探讨如何使用MATLAB求解二元函数的自变量。

二元函数是指具有两个自变量的函数，可以表示为f(x, y)。

在MATLAB中，我们可以通过给定函数值来求解对应的自变量。

具体而言，我们可以通过给定f(x, y)的函数值来求解x和y的取值。

我们需要明确给定的函数值。

假设我们已知二元函数f(x, y)在某些特定点的函数值，我们的目标是求解x和y的取值。

为了使用MATLAB求解这个问题，我们可以使用插值方法。

插值是一种通过已知数据点来推断未知数据点的方法。

在MATLAB中，有多种插值方法可供选择，如线性插值、多项式插值和样条插值等。

下面我们将以一个具体的例子来说明如何使用MATLAB求解二元函数的自变量。

假设我们有一个二元函数f(x, y)，我们已知它在以下四个点的函数值：f(1, 1) = 2f(1, 2) = 4f(2, 1) = 3f(2, 2) = 6我们的目标是求解x和y的取值。

我们可以使用线性插值方法来推断其他点的函数值。

线性插值是一种简单但有效的插值方法，它假设函数在已知点之间是线性的。

在MATLAB中，我们可以使用interp2函数来进行线性插值。

interp2函数的用法如下：z = interp2(x, y, v, xi, yi)其中，x和y是已知点的横纵坐标，v是已知点的函数值，xi和yi 是待求函数值的横纵坐标，z是待求函数值。

根据我们的例子，我们可以将已知点的横纵坐标和函数值输入interp2函数来求解其他点的函数值。

具体代码如下：x = [1 1 2 2];y = [1 2 1 2];v = [2 4 3 6];xi = [1.5];yi = [1.5];z = interp2(x, y, v, xi, yi)运行上述代码，我们可以得到z的值为4.5。

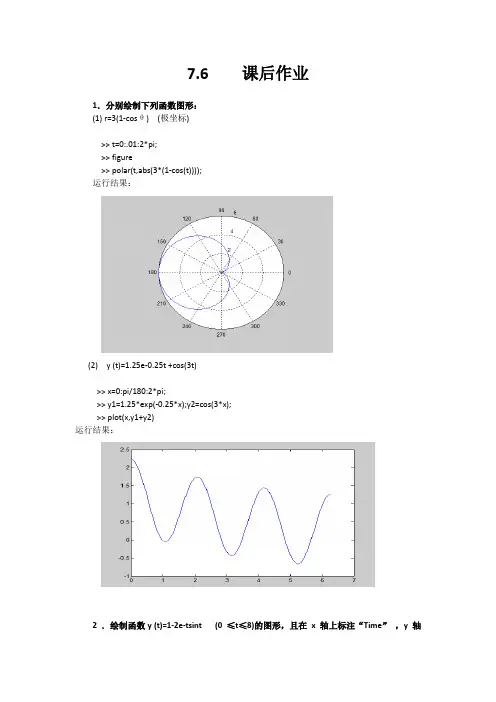
7.6 课后作业1．分别绘制下列函数图形：(1) r=3(1-cosθ) (极坐标)>> t=0:.01:2*pi;>> figure>> polar(t,abs(3*(1-cos(t))));运行结果：(2) y (t)=1.25e-0.25t +cos(3t)>> x=0:pi/180:2*pi;>> y1=1.25*exp(-0.25*x);y2=cos(3*x);>> plot(x,y1+y2)运行结果：2 ．绘制函数y (t)=1-2e-tsint (0 ≤t≤8)的图形，且在x 轴上标注“Time”，y 轴上标注“Amplitude”，图形的标题为“Decaying Oscillating Exponential”。

>> x=0:0.01:8;>> y=1-2*exp(-1*x).*sin(x);>> figure>> plot(x,y)>> xlabel('Time');ylabel('Amplitude');>> title('Decaying Oscillating Exponential');运行结果：3 ．在同一图中绘制下列两条曲线(x ∈[0,25]内) ：(1) y 1(t)=2.6e(-0.5x) cos(0.6x)+0.8 ；(2) y 2(t)=1.6cos(3x)+sin(x)要求用不同的颜色和线型分别表示y 1(t) 和y 2(t) ，并给图形加注解。

>> x=0:0.1:25;>> y1=2.6*exp(-0.5*x).*cos(0.6*x)+0.8;>> y2=1.6*cos(3*x)+sin(x);>> figure>> plot(x,y1,'r-X',x,y2,'b--.');>> legend('y1=2.6*exp(-0.5*x).*cos(0.6*x)+0.8','y2=1.6*cos(3*x)+sin(x)')4 ．在一个图形窗口下绘制两个子图，分别显示下列曲线：(1)y =sin2xcos3x ；(2) y =0.4 x要求给x 轴、y 轴加标注，每个子图加标题。

matlab中mesh命令mesh命令是MATLAB中用于绘制三维曲面的函数，它可以将离散的数据点连接成平滑的曲面。

本文将介绍mesh命令的使用方法和一些相关知识。

我们来了解一下mesh命令的基本语法。

在MATLAB命令窗口中输入"help mesh"即可查看详细的使用说明。

一般情况下，mesh命令的语法如下：mesh(X, Y, Z)其中，X、Y和Z是三个相同大小的矩阵，分别表示曲面上各个点的横坐标、纵坐标和高度。

通过这些点的连接，mesh命令可以绘制出一个三维曲面。

下面我们来看一个具体的例子。

假设我们希望绘制一个二元函数z = f(x, y) = sin(x) + cos(y)，我们可以先生成一个横坐标和纵坐标的网格矩阵，然后计算对应的高度矩阵。

具体的代码如下：```matlabx = linspace(-pi, pi, 100);y = linspace(-pi, pi, 100);[X, Y] = meshgrid(x, y);Z = sin(X) + cos(Y);mesh(X, Y, Z);运行上述代码后，MATLAB会自动打开一个新的窗口，显示出绘制的三维曲面。

通过鼠标的拖动和缩放，我们可以自由地查看曲面的各个部分。

除了基本的绘制功能，mesh命令还提供了一些可选参数，用于进一步定制曲面的外观。

例如，我们可以使用以下代码将曲面的颜色设置为红色，并添加网格线：```matlabmesh(X, Y, Z, 'FaceColor', 'red', 'EdgeColor', 'black');```mesh命令还可以与其他绘图命令结合使用，实现更加复杂的图形效果。

例如，我们可以使用以下代码将曲面绘制在一个已有的三维坐标系上：```matlabfigure;hold on;plot3(X(:), Y(:), Z(:), 'o', 'MarkerFaceColor', 'blue', 'MarkerEdgeColor', 'blue');mesh(X, Y, Z);hold off;运行上述代码后，我们会得到一个包含散点和曲面的图形，其中散点表示曲面上的各个数据点。

matlab 求解二元方程
Matlab是一种强大的计算软件，可以用来解决各种数学问题，包括求解二元方程。

二元方程是指只有两个未知数的方程，通常表示为ax + by = c和dx + ey = f。

如果我们知道a、b、c、d、e和f 的值，我们可以使用Matlab求解这个方程组，找到x和y的值。

要使用Matlab求解二元方程，需要使用线性代数中的求解方法。

具体步骤如下：
1. 将方程表示为矩阵形式。

将系数和常数项分别表示为矩阵A 和矩阵B，得到方程组AX = B。

2. 使用Matlab中的“linsolve”函数求解方程组。

该函数接受两个参数：A和B。

它返回一个向量X，其中包含方程组的解。

3. 使用向量X计算x和y的值。

根据方程ax + by = c和dx + ey = f，我们可以得到x和y的计算公式。

使用Matlab求解二元方程非常简单，只需几行代码即可完成。

以下是一个示例：
% 定义方程的系数和常数项
A = [2 3; 4 5];
B = [8; 14];
% 求解方程组
X = linsolve(A, B);
% 计算x和y的值
x = X(1);
y = X(2);
disp(['x = ', num2str(x)]);
disp(['y = ', num2str(y)]);
这将输出x = 1，y = 2，这就是方程的解。

MATLAB绘图与图形处理人们很难从一大堆原始的数据中发现它们的含义，而数据图形恰能使视觉感官直接感受到数据的许多内在本质，发现数据的内在联系。

MATLAB可以表达出数据的二维，三维，甚至四维的图形。

通过图形的线型，立面，色彩，光线，视角等属性的控制，可把数据的内在特征表现得淋漓尽致。

下面我们分别介绍图形的命令。

7.1 二维图形7.1.1 基本平面图形命令命令1 plot功能线性二维图。

在线条多于一条时，若用户没有指定使用颜色，则plot循环使用由当前坐标轴颜色顺序属性（current axes ColorOrder property）定义的颜色，以区别不同的线条。

在用完上述属性值后，plot又循环使用由坐标轴线型顺序属性（axes LineStyleOrder property）定义的线型，以区别不同的线条。

用法plot(X,Y) 当X,Y均为实数向量，且为同维向量（可以不是同型向量），X=[x(i)]，Y=[y(i)]，则plot(X,Y)先描出点(x(i)，y(i))，然后用直线依次相连；若X，Y为复数向量，则不考虑虚数部分。

若X，Y均为同维同型实数矩阵，X = [X(i)]，Y = [Y(i)]，其中X(i),Y(i)为列向量，则plot(X,Y)依次画出plot(X(i),Y(i))，矩阵有几列就有几条线；若X，Y中一个为向量，另一个为矩阵，且向量的维数等于矩阵的行数或者列数，则矩阵按向量的方向分解成几个向量，再与向量配对分别画出，矩阵可分解成几个向量就有几条线；在上述的几种使用形式中，若有复数出现，则复数的虚数部分将不被考虑。

plot(Y) 若Y为实数向量，Y的维数为m，则plot(Y)等价于plot(X,Y)，其中x=1：m；若y 为实数矩阵，则把y按列的方向分解成几个列向量，而y 的行数为n，则plot(Y)等价于plot(X,Y)其中x=[1;2;…;n]；在上述的几种使用形式中，若有复数出现，则复数的虚数部分将不被考虑。

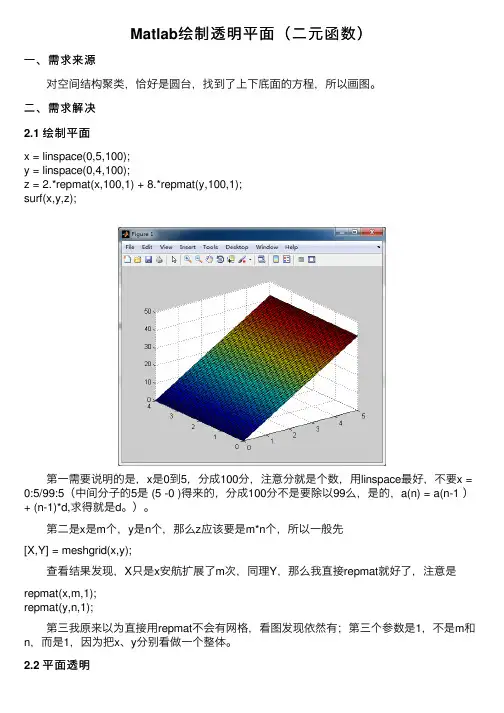
Matlab绘制透明平⾯（⼆元函数）
⼀、需求来源
对空间结构聚类，恰好是圆台，找到了上下底⾯的⽅程，所以画图。

⼆、需求解决
2.1 绘制平⾯
x = linspace(0,5,100);
y = linspace(0,4,100);
z = 2.*repmat(x,100,1) + 8.*repmat(y,100,1);
surf(x,y,z);
第⼀需要说明的是，x是0到5，分成100分，注意分就是个数，⽤linspace最好，不要x = 0:5/99:5（中间分⼦的5是 (5 -0 )得来的，分成100分不是要除以99么，是的，a(n) = a(n-1 ）+ (n-1)*d,求得就是d。

）。

第⼆是x是m个，y是n个，那么z应该要是m*n个，所以⼀般先
[X,Y] = meshgrid(x,y);
查看结果发现，X只是x安航扩展了m次，同理Y，那么我直接repmat就好了，注意是repmat(x,m,1);
repmat(y,n,1);
第三我原来以为直接⽤repmat不会有⽹格，看图发现依然有；第三个参数是1，不是m和n，⽽是1，因为把x、y分别看做⼀个整体。

2.2 平⾯透明
x = linspace(0,5,100);
y = linspace(0,4,100);
z = 2.*repmat(x,100,1) + 8.*repmat(y,100,1);
surf(x,y,z);
hold on;
alpha(.3);
shading interp
⾸先是alpha函数设置透明度，但是⽹格还有，那么加上shading interp。

二元一次函数曲线拟合的matlab实
现
，
二元一次函数曲线拟合的Matlab实现是一种让机器在获得规定数据的情况下，计
算机根据函数形式拟合出拟合曲线的技术。

它在数学中是一种重要的数学模型，既可以预测改变数据及推算出有规律的变化趋势呈现出具有参考价值的一种分析结果。

Matlab 是一款数学软件套件，具有较强的数字计算功能及图形界面操作的特点，使用 Matlab 可以确定该数据的线性函数拟合曲线，比如用 Matlab 运用polyfit 和 polyval 函数，但是在运用之前要先先定义好二元一次函数的形式的
参数，将数据集转换成矩阵，然后用 polyfit 函数实现拟合曲线。

之后可以随意
选择多少个点根据当前的曲线来提取坐标，把这些坐标用 polyval 函数插值，生
成拟合误差曲线来衡量拟合的精度。

通过运用Matlab生成合适的拟合曲线，可以帮助我们分析相应数据特征，Universities和研究所也通常用该拟合曲线来研究数值之间的关系及时间序列，
为未来可能出现的变化状态做准备和规划，保证数据的准确性和可靠性。

这也是互联网急需的一项能力，既可用于分析数据，同时也可以研判实践中经常发生的大量复杂变量间的关系，提高运算实用性。

MATL AB绘制二元函数的图形【实验目的】1.了解二元函数图形的绘制。

2.了解空间曲面等高线的绘制。

3.了解多元函数插值的方法。

4.学习、掌握MATLAB软件有关的命令。

【实验内容】画出函数22yz+=的图形，并画出其等高线。

x【实验准备】1.曲线绘图的MATLAB命令MATLAB中主要用mesh,surf命令绘制二元函数图形。

主要命令mesh（x，y，z）画网格曲面，这里x，y，z是数据矩阵，分别表示数据点的横坐标，纵坐标和函数值，该命令将数据点在空间中描出，并连成网格。

surf（x，y，z）画完整曲面，这里x，y，z是数据矩阵，分别表示数据点的横坐标，纵坐标和函数值，该命令将数据点所表示曲面画出。

【实验重点】1. 二元函数图形的描点法2. 曲面交线的计算3. 地形图的生成【实验难点】1. 二元函数图形的描点法2. 曲面交线的计算【实验方法与步骤】练习1画出函数22y=的图形，其中]3,3xz+⨯-yx。

∈,[]3,3[(-)用MATLAB作图的程序代码为>>clear;>>x=-3:0.1:3; %x的范围为[-3，3]>>y=-3:0.1:3; %y的范围为[-3，3]>>[X,Y]=meshgrid(x,y); %将向量x,y指定的区域转化为矩阵X,Y >>Z=sqrt(X.^2+Y.^2); %产生函数值Z>>mesh(X,Y,Z)运行结果为图5.3如果画等高线，用contour，contour3命令。

contour画二维等高线。

contour3画三维等高线。

画图5.3所示的三维等高线的MA TLAB 代码为>>clear;>>x=-3:0.1:3;>>y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);>>Z=sqrt(X.^2+Y.^2);>>contour3(X,Y,Z,10); %画10条等高线>>xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis'); %三个坐标轴的标记>>title('Contour3 of Surface') %标题>>grid on %画网格线运行结果为图5.4如果画图5.4所示的二维等高线，相应的MATLAB代码为>>clear;x=-3:0.1:3;y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2);>>contour (X,Y,Z,10);>>xlabel('X-axis'),ylabel('Y-axis');>>title('Contour3 of Surface')>>grid on运行结果为如果要画z=1的等高线，相应的MATLAB代码为>>clear;x=-3:0.1:3;y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2);>>contour(X,Y,Z,[1 1])运行结果为练习2 二次曲面的方程如下222222x y z d a b c++= 讨论参数a ,b ,c 对其形状的影响。

一、介绍Matlab是一款用于科学计算和技术计算的软件，拥有强大的绘图功能，可以用于绘制各种图形、曲线和函数图像。

在Matlab中，使用plot函数可以绘制二元函数的图像，通过调整参数和设置属性，可以实现不同风格和效果的图像展示。

本文将详细介绍在Matlab中如何绘制二元函数的图像，包括基本的绘图方法和常用的设置技巧。

二、绘制二元函数图像的基本方法1. 准备数据在使用Matlab绘制二元函数的图像前，首先需要准备数据。

通常可以通过生成x、y坐标的网格点，然后计算每个点对应的函数值，从而得到二元函数在指定区域内的数据集。

2. 使用plot函数一旦准备好了数据集，就可以使用Matlab的plot函数进行绘图。

plot函数的基本语法为：plot(x, y)，其中x和y分别代表要绘制的点的横坐标和纵坐标。

通过调用plot函数，可以将计算得到的数据点连接起来，形成二元函数的图像。

3. 添加标签和标题为了让图像更加清晰和直观，通常需要添加x和y轴的标签，以及整个图像的标题。

在Matlab中，可以使用xlabel、ylabel和title函数来分别添加x轴、y轴和标题标签。

4. 设置图像属性通过设置图像的属性，可以调整图像的风格和效果。

常用的属性包括线型、线宽、颜色和标记符号等。

在Matlab中，可以使用参数-字符串对的形式来设置图像的属性，例如'LineStyle'、'LineWidth'、'Color'和'Marker'等。

三、绘制常见二元函数的图像在Matlab中，可以绘制各种类型的二元函数的图像，包括线性函数、二次函数、三角函数、指数函数、对数函数等。

下面将分别介绍如何绘制这些常见二元函数的图像。

1. 绘制线性函数图像线性函数的一般形式为y=ax+b，其中a和b分别为常数。

在Matlab 中，可以通过设置a和b的值，然后使用plot函数绘制线性函数的图像。

《MATLA‎B语言》课程论文用MATL‎A B绘制一‎元函数和二‎元函数的图‎象姓名：**学号： *****‎*****‎ 5专业：通信工程班级： 2010级‎通信1班指导老师：***学院：物理电气信‎息学院完成日期：2011.12.20用MATL ‎A B 绘制一‎元函数和二‎元函数的图‎像（马军 12010‎24524‎ 5 2010级‎通信工程1‎班）【摘要】大学物理力‎学中涉及许‎多复杂的数‎值计算问题‎，例如非线性‎问题，对其手工求‎解较为复杂‎，而MATL ‎AB 语言正‎是处理非线‎性问题的很‎好工具，既能进行数‎值求解，又能绘制有‎关曲线，非常方便实‎用。

另外，利用其可减‎少工作量，节约时间，加深理解，同样可以培‎养应用能力‎。

【关键词】一元函数 二元函数 MATLA ‎ B 图像的绘制‎一、问题的提出‎MATLA ‎B 语言是当‎今国际上科‎学界(尤其是自动‎控制领域)最具影响力‎、也是最有活‎力的软件。

它提供了强‎大的科学运‎算、灵活的程序‎设计流程、高质量的图‎形可视化与‎界面设计、便捷的与其‎他程序和语‎言接口的功‎能。

MATLA ‎B 语言在各‎国高校与研‎究单位起着‎重大的作用‎.它是一种集‎数值计算、符号运算、可视化建模‎、仿真和图形‎处理等多种‎功能…二、实验内容1．平面曲线的‎表示形式对于平面曲‎线，常见的有三‎种表示形式‎，即以直角坐‎标方程],[),(b a x x f y ∈=，以参数方程‎],[),(),(b a t t y y t x x ∈==，和以极坐标‎],[),(b a r r ∈=ϕϕ表示等三种‎形式。

2．曲线绘图的‎M ATLA ‎B 命令MATLA ‎B 中主要用‎p lot,fplot ‎二种命令绘‎制不同的曲‎线。

plot(x,y) 作出以数据‎(x (i),y(i))为节点的折‎线图，其中x,y 为同维数‎的向量。

plot(x1,y1,x2,y2,…) 作出多组数‎据折线图 fplot ‎(‘fun’,[a,b]) 作出函数f ‎u n 在区间‎[a,b]上的函数图‎。

图4-4 图4-5 数学实验四 用Matlab 软件作二元函数的图象一、空间曲线调用格式：plot3(x1,y1,z1,x2,y2,z2,…,xn,yn,zn)其中xi 、yi 和zi 为分别是长度相同的向量，用于存储xi 坐标、yi 坐标和zi 坐标数据，i=1,2,…,n ．例1 在同一坐标系中分别作出三维曲线 ==x x z x x y cos sin 和+=−=2442x z x y 在]6,0[π∈x 上的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：x=0:pi/50:6*pi;y1=x.*sin(x);z1=x.*cos(x);y2=2*x-1;z2=4*x-8;plot3(x,y1,z1,x,y2,z2);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')legend('圆锥螺线','空间直线')取名为exa1保存，再在命令窗口中输入命令exa1，程序运行结果如图4-4．说明：若要作单根曲线，和前面plot 函数一样，只是多了一个立坐标．二、空间曲面1．三维网格图调用格式一：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)plot3(x,y,z)其中x 、y 和z 为长度相同的向量，分别用于存储x 坐标、y 坐标和z 坐标数据． 例2 作出空间平面324=+−z y x 的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-3:0.1:3,-2:0.1:3); %产生一个x,y 平面上51×61的网格z=3-4*x+2*y;plot3(x,y ,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')title('4x-2y+z=3')取名为exa2保存，再在命令窗口中输入命令exa2，程序运行结果如图4-5．例3 作出空间曲面2222sin y x y x z ++=在区域图4-7图4-8}8||,8|||),{(≤≤y x y x 上的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-8:0.1:8);r=sqrt(x.^2+y.^2); %产生对应的x,y 坐标用点幂z=sin(r)./r; %产生对应于x,y 的z 坐标用点除plot3(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa3保存，再在命令窗口中输入命令exa3，程序运行结果如图4-6．调用格式二：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)mesh(x,y,z)例4 在x 、y 平面内选取一个区域，作出空间曲面22y xe z −−=的图象． 解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-4:0.1:3,-3:.1:2); %产生一个x,y 平面上51×71的网格z=exp(-x.^2-y.^2);mesh(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa2保存，再在命令窗口中输入命令exa2，程序运行结果如图4-7．2．三维曲面图调用格式：[x,y]=meshgrid(x1:h1:x2,y1:h2:y2)z=f(x,y)surf(x,y,z) 说明：surf 函数可借助shading 函数作平滑和插值处理，而shading 函数有三个参数，分别为flat （作平滑处理）、interp （去掉连接线条，在各片之间使用颜色插值）和faceted （默认值，对前面两种参数之一的作用进行还原）．例5 用子图分别作出马鞍面22y x z −=在区域}2||,1|||),{(≤≤y x y x 图和经插值处理的图．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y]=meshgrid(-1:0.1:1,-2:.1:2);z=x.^2-y.^2;subplot(1,2,1),surf(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')title('z=x^2-y^2');subplot(1,2,2),surf(x,y,z);图4-9 图4-10xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')shading interp %插值处理title('z=x^2-y^2的插值处理图')取名为exa5保存，再在命令窗口中输入命令exa5，程序运行结果如图4-8．3．柱面图调用格式一：[x,y,z]=cylinder(R,N)mesh(x,y,z)其中，R 是一个向量，其坐标分量依次对应柱面各横截面的半径，Ｎ是多边形的边数．默认值是Ｒ＝[1,1]，Ｎ＝20．例6 作出正六棱柱在Ｒ＝[２,２]的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y,z]=cylinder([2,2],6);mesh(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')hidden off %显示隐含线，若不想显示隐含线，则取消此命令或设置为hidden on取名为exa6保存，再在命令窗口中输入命令exa6，程序运行结果如图4-9． 调用格式二：[x,y,z]=cylinder(R,N)surf(x,y,z)其中，R 、Ｎ的意义和上面一样．例7 作出正十棱台在Ｒ＝[1,2]的图象．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：[x,y,z]=cylinder([1,2],10);surf(x,y,z);xlabel('x 轴'),ylabel('y 轴'),zlabel('z 轴')取名为exa7保存，再在命令窗口中输入命令exa7，程序运行结果如图4-10．说明：若要作正棱锥，只须取Ｒ的某个分量为0即可．4．球面图调用格式：[x,y,z]=sphere(N)surf(x,y,z) 其中，N （N>2）是球面的边数．默认值是Ｎ＝20．sphere(N)不返回坐标，直接绘出球面．例8 以子图形式分别作出N=5、20、40和40并作平滑处理的球．解 打开Ｍ文件编辑窗口，在其中输入下面命令集：subplot(2,2,1)sphere(5);title('子图1')subplot(2,2,2),sphere;title('子图2')subplot(2,2,3)[x,y,z]=sphere(40);surf(x,y,z);title('子图3')subplot(2,2,4)[x,y,z]=sphere(40);surf(x,y,z);shading flat %对球面作平滑处理title('子图4') 取名为exa8保存，再在命令窗口中输入命令exa8，程序运行结果如图4-11．三、上机实验1．用help 命令查看函数plot3，mesh 和surf 等的用法．2．上机验证上面各例．3．作相关小节练习中空间曲线和曲面的图象．图4-11。

matlab二元函数已知函数值求自变量
在数学中，二元函数是指具有两个自变量的函数，通常表示为f(x,y)。

在实际应用中，我们经常需要求解二元函数在某些自变量取值下的函数值。

这时，我们可以利用已知的函数值来反推自变量的取值。

在matlab中，我们可以使用插值函数来实现这一过程。

插值函数是一种通过已知数据点来估计未知数据点的方法。

在二元函数中，我们可以使用二维插值函数来实现自变量的求解。

二维插值函数的基本思想是利用已知的函数值来构建一个二元函数的插值函数，然后通过插值函数来估计未知自变量的取值。

在matlab中，常用的二维插值函数有interp2和griddata。

interp2函数可以用来对二元函数进行插值，其基本语法为：
Zq = interp2(X,Y,Z,Xq,Yq)
其中，X、Y和Z分别表示已知数据点的自变量和函数值，Xq和Yq表示待求解的自变量，Zq表示插值函数在(Xq,Yq)处的函数值。

griddata函数也可以用来对二元函数进行插值，其基本语法为：
Zq = griddata(X,Y,Z,Xq,Yq)
其中，X、Y和Z分别表示已知数据点的自变量和函数值，Xq和
Yq表示待求解的自变量，Zq表示插值函数在(Xq,Yq)处的函数值。

需要注意的是，二维插值函数的精度和效率受到数据点的数量和分布的影响。

因此，在使用二维插值函数时，我们需要根据实际情况选择合适的插值方法和参数，以获得更准确的结果。

利用matlab中的二维插值函数，我们可以方便地求解二元函数在某些自变量取值下的函数值。

这为我们在实际应用中解决问题提供了有力的工具和方法。