《化工热力学》第4章 均相敞开系统热力学及相平衡准则课后习题答案
- 格式:doc
- 大小:1.61 MB
- 文档页数:12

习题四一、是否题M M.4—1 对于理想溶液的某一容量性质M,则 i i解:否4—2 在常温、常压下,将10cm3的液体水与20 cm3的液体甲醇混合后,其总体积为30 cm3。
解:否4-3温度和压力相同的两种纯物质混合成理想溶液,则混合过程的温度、压力、焓、Gibbs自由能的值不变。
解:否4-4对于二元混合物系统,当在某浓度范围内组分2符合Henry规则,则在相同的浓度范围内组分1符合Lewis-Randall规则.解:是4-5在一定温度和压力下的理想溶液的组分逸度与其摩尔分数成正比.解:是4-6理想气体混合物就是一种理想溶液.解:是4-7对于理想溶液,所有的混合过程性质变化均为零。
解:否4-8对于理想溶液所有的超额性质均为零。
解:否4-9 理想溶液中所有组分的活度系数为零。
解:否4—10 系统混合过程的性质变化与该系统相应的超额性质是相同的. 解:否4—11理想溶液在全浓度范围内,每个组分均遵守Lewis-Randall 定则. 解:否4—12 对理想溶液具有负偏差的系统中,各组分活度系数i γ均 大于1。
解:否4-13 Wilson 方程是工程设计中应用最广泛的描述活度系数的方程。
但它不适用于液液部分互溶系统。
解:是二、计算题4-14 在一定T 、p 下,二元混合物的焓为 2121x cx bx ax H ++= 其中,a =15000,b =20000,c = — 20000 单位均为-1J mol ⋅,求 (1) 组分1与组分2在纯态时的焓值1H 、2H ;(2) 组分1与组分2在溶液中的偏摩尔焓1H 、2H 和无限稀释时的偏摩尔焓1∞H 、2∞H 。
解:(1)1111lim 15000J mol -→===⋅x H H a2121lim 20000J mol -→===⋅x H H b(2)按截距法公式计算组分1与组分2的偏摩尔焓,先求导:()()()12121111111d dd d d11d H ax bx cx x x x ax b x cx x x =++=+-+-⎡⎤⎣⎦12=-+-a b c cx将1d d Hx 代入到偏摩尔焓计算公式中,得()()()()()()11112121111111112122d 1d (1)211221H H H x x ax bx cx x x a b c cx ax b x cx x a b c cx x a b c cx a c x a cx =+-=+++--+-=+-+-+-+---+-=+-=+()()()()21121211111111121d 2d 112HH H x ax bx cx x x a b c cx x ax b x cx x x a b c cx b cx =-=++--+-=+-+---+-=+无限稀释时的偏摩尔焓1∞H 、2∞H 为:()()2-1112012-122111221lim lim 150002000035000J mol lim lim 200002000040000J molx x x x H H a cx H H b cx∞→→∞→→==+=+=⋅==+=+=⋅4—15 在25℃,1atm 以下,含组分1与组分2的二元溶液的焓可以由下式表示:121212905069H x x x x x x =++⋅+()式中H 单位为-1cal mol ⋅,1x 、2x 分别为组分1、2的摩尔分数,求 (1) 用1x 表示的偏摩尔焓1H 和2H 的表达式; (2) 组分1与2在纯状态时的1H 、2H ;(3) 组分1与2在无限稀释溶液的偏摩尔焓1∞H 、2∞H ;(4) ΔH 的表达式;(5) 1x =0。



化工热力学课后答案第1章绪言—、是否题1. 封闭体系的体积为一常数。
(错)2. 封闭体系中有两个相, 。
在尚未达到平衡时,, 两个相都是均相敞开体系;达到平衡时,则,两个相都等价于均相封闭体系。
(对)3. 理想气体的焓和热容仅是温度的函数。
(对)4. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5. 封闭体系的1mol 气体进行了某一过程, 其体积总是变化着的, 但是初态和终态的体积相T 2等,初态和终态的温度分别为 T [和丁2,则该过程的 UC V dT ;同样,对于初、终态T iT 2压力相等的过程有 HC p dT 。
(对。
状态函数的变化仅决定于初、 终态与途径无关。
)T 1二、填空题状态函数的特点是: ________ 。
封闭体系中,温度是 T 的1mol 理想气体从(P , V )等温可逆地膨胀到(P ,V f ),则所做的 功为 W revRTl nV i V f (以 V 表示)或 W rev RT l nP f P (以 P 表示)。
C PP T1T 1。
1.3. 封闭体系中的imol 理想气体(已知C pg ),按下列途径由T 、P i 和V 可逆地变化至P 2,则A 等容过程的 W = _,Q= Cp 1RP 2 P 2P i/C Pg RP 1 1 T 1 , H=B等温过程的RTln l,^RTln t,U= 0 ,H=_0 ___ 。
解:EOSW revV 2 b RTl n丄 V 1 bRTln 纟V 1999In 2 1.0007222. 对于c P为常数的理想气体经过一绝热可逆过程,状态变化符合下列方程解: 3. 解: T 1 P 1(1),其式又是如何?以上a 、b 、 理想气体的绝热可逆过程,C ;gRdTT 22a Rb TT 1aln 旦 b T 2T1RT dV V cT dTCigC !,试问,对于C P a bTcT 2的理想气体,上述关系c 为常数。



第1章 绪言一、是否题1. 封闭体系的体积为一常数。
(错)2. 封闭体系中有两个相βα,。
在尚未达到平衡时,βα,两个相都是均相敞开体系;达到平衡时,则βα,两个相都等价于均相封闭体系。
(对)3. 理想气体的焓和热容仅是温度的函数。
(对)4. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5. 封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的⎰=21T T V dT C U ∆;同样,对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
(对。
状态函数的变化仅决定于初、终态与途径无关。
) 二、填空题1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。
2. 封闭体系中,温度是T 的1mol 理想气体从(P i ,V i )等温可逆地膨胀到(P f ,V f ),则所做的以V 表示)(以P 表示)。
3. 封闭体系中的1mol 理想气体(已知igP C ),按下列途径由T 1、P 1和V 1可逆地变化至P 2,则A 等容过程的 W = 0 ,Q =()1121T P P R C ig P ⎪⎪⎭⎫ ⎝⎛--,∆U =()1121T P P R C igP ⎪⎪⎭⎫ ⎝⎛--,∆H =1121T P P C ig P ⎪⎪⎭⎫ ⎝⎛-。
B 等温过程的 W =21lnP P RT -,Q =21ln P PRT ,∆U = 0 ,∆H = 0 。
C 绝热过程的 W =()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛--11211igPC RigPP P R V P R C ,Q = 0 ,∆U =()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-11211PC RigPP P R V P R C ,∆H =1121T P P C igPC R ig P ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛。

4-11 解:(1)已知 )1025(450300212121x x x x x x H +++= (A ) 由于 211x x -=故 )1025(450300212121x x x x x x H +++=)]1(1025)[1()1(450300111111x x x x x x -+-+-+=31211155140450x x x -+-= (B ) 根据 P T x Hx H H ⋅∂∂++=))(1(11 P T x H x H H ⋅∂∂-=)(112 其中211.14510140)(x x x HP T -+-=∂∂ 则:)4510140)(1(1551404502111312111x x x x x x H -+--+-+-= 31211305010310x x x +-+= (C ) )4510140(1551404502111312112x x x x x x H -+---+-= 3121305450x x +-= (D) (2) 将11=x 及01=x 分别代入式(B ),得纯组元的焓H ,和2H mol J H ⋅=3001 mol J H ⋅=4502(3)∂1H 和∂2H 是指在01=x 及11=x 时的1H 和2H 的极限值。
将01=x 代入式(C )中得 mol J H ⋅=∂3101 将11=x 代入式(D )中得 mol J H ⋅=∂4752 4-13解:根据摩尔性质与偏摩尔性质间的关系得 111)1(dx dMx M M -+=112dx dMx M M -= 当V M =时111)1(dx dMx V V -+= 112dx dMx V V += 已知21164.28.164.109x x V --=得1128.58.16x dx dV --= 将V 及1dx dV代入1V 和2V 的表达式中 得211164.228.56.92x x V +-= (A ) 21264.24.109x V += (B )由式(A ) 当11→x 时,得96.891=V 由式(B ) 当01→x 时,得4.1092=V因为∑-=∆)(iiiV V x V所以)()(222111V V x V V x V -+-=∆)4.10964.24.109)(1()96.8964.228.56.92(2112111-+-+-+-=x x x x x 31213121164.264.264.228.564.2x x x x x -++-= 21164.264.2x x -= )1(64.211x x -= 2164.2x x = 4-14解:根据Gibbs-Duhem 方程∑=0)(,P T i i M d x得恒温恒压下 02211=+M d x M d x或 222122111x M d x dx M d x dx M d x =-= 当i i H M =时,得122111dx H d x dx H d x -= 已知 22111x b a H += 21222x b a H +=则1111122x b b dx H d +-=12122x b dx H d = 211111211111112)1(222x x b x x b x b x b dx H d x -=-=+-= 1221222x x b dx H d x -=- 只有当21b b =时 122111dx H d x dx H d x -= 结论得证。

化工热力学习题及详细解答习题 (2)第1章绪言 (2)第2章 P-V-T关系和状态方程 (4)第3章均相封闭体系热力学原理及其应用 (8)第4章非均相封闭体系热力学 (13)第5章非均相体系热力学性质计算 (19)第6章例题 (27)答案 (40)第1章绪言 (40)第2章 P-V-T关系和状态方程 (44)第3章均相封闭体系热力学原理及其应用 (51)第4章非均相封闭体系热力学 (68)第5章非均相体系热力学性质计算 (87)附加习题 (103)第2章 (103)第3章 (104)第4章 (107)第5章 (109)习题第1章 绪言一、是否题1. 孤立体系的热力学能和熵都是一定值。
2. 封闭体系的体积为一常数。
3. 封闭体系中有两个相βα,。
在尚未达到平衡时,βα,两个相都是均相敞开体系;达到平衡时,则βα,两个相都等价于均相封闭体系。
4. 理想气体的焓和热容仅是温度的函数。
5. 理想气体的熵和吉氏函数仅是温度的函数。
6. 要确定物质在单相区的状态需要指定两个强度性质,但是状态方程 P=P (T ,V )的自变量中只有一个强度性质,所以,这与相律有矛盾。
7. 封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的⎰=21T T V dT C U ∆;同样,对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
8. 描述封闭体系中理想气体绝热可逆途径的方程是γγ)1(1212-⎪⎪⎭⎫⎝⎛=P P T T (其中igV ig P C C =γ),而一位学生认为这是状态函数间的关系,与途径无关,所以不需要可逆的条件。
9. 自变量与独立变量是一致的,从属变量与函数是一致的。
10. 自变量与独立变量是不可能相同的。
二、填空题1. 状态函数的特点是:___________________________________________。

第4章 非均相封闭体系热力学 一、是否题1. 偏摩尔体积的定义可表示为{}{}ii x P T i n P T ii x V nnV V ≠≠⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂=,,,,∂。
(错。
因对于一个均相敞开系统,n 是一个变数,即(){}0,,≠∂∂≠in P T i n n )2. 在一定温度和压力下的理想溶液的组分逸度与其摩尔分数成正比。
(对。
即常数===),(,ˆP T f f x f f i ii is i )3. 理想气体混合物就是一种理想溶液。
(对)4. 对于理想溶液,所有的混合过程性质变化均为零。
(错。
V ,H ,U ,C P ,C V 的混合过程性质变化等于零,对S ,G ,A 则不等于零) 5. 对于理想溶液所有的超额性质均为零。
(对。
因is EM M M-=)6. 理想溶液中所有组分的活度系数为零。
(错。
理想溶液的活度系数为1)7. 体系混合过程的性质变化与该体系相应的超额性质是相同的。
(错。
同于4)8. 对于理想溶液的某一容量性质M ,则__i i M M =。
(错,同于4)9.理想气体有f=P ,而理想溶液有i i ϕϕ=ˆ。
(对。
因i i i i i i is iisiPf Px x f Px f ϕϕ====ˆˆ) 10. 温度和压力相同的两种理想气体混合后,则温度和压力不变,总体积为原来两气体体积之和,总热力学能为原两气体热力学能之和,总熵为原来两气体熵之和。
(错。
总熵不等于原来两气体的熵之和)11. 温度和压力相同的两种纯物质混合成理想溶液,则混合过程的温度、压力、焓、热力学能、吉氏函数的值不变。
(错。
吉氏函数的值要发生变化) 12. 因为G E (或活度系数)模型是温度和组成的函数,故理论上i γ与压力无关.(错。
理论上是T ,P ,组成的函数。
只有对低压下的液体,才近似为T 和组成的函数)13. 在常温、常压下,将10cm 3的液体水与20 cm 3的液体甲醇混合后,其总体积为 30 cm 3。
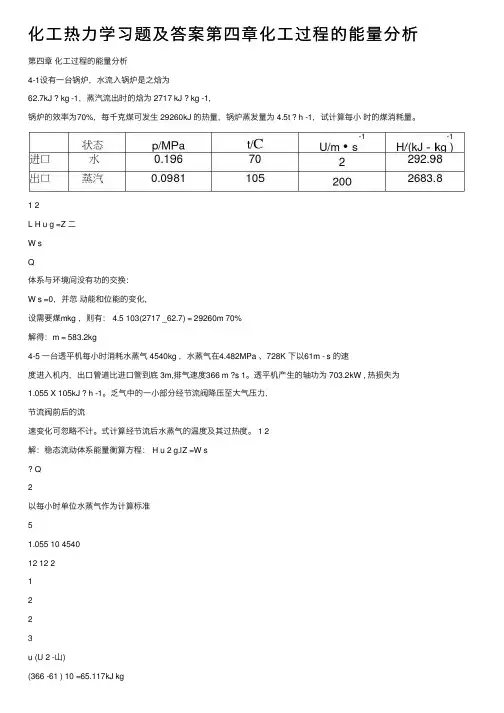
化⼯热⼒学习题及答案第四章化⼯过程的能量分析第四章化⼯过程的能量分析4-1设有⼀台锅炉,⽔流⼊锅炉是之焓为62.7kJ ? kg -1,蒸汽流出时的焓为 2717 kJ ? kg -1,锅炉的效率为70%,每千克煤可发⽣ 29260kJ 的热量,锅炉蒸发量为 4.5t ? h -1,试计算每⼩时的煤消耗量。
1 2L H u g =Z ⼆W sQ体系与环境间没有功的交换:W s =0,并忽动能和位能的变化,设需要煤mkg ,则有: 4.5 103(2717 _62.7) = 29260m 70%解得:m = 583.2kg4-5 ⼀台透平机每⼩时消耗⽔蒸⽓ 4540kg ,⽔蒸⽓在4.482MPa 、728K 下以61m - s 的速度进⼊机内,出⼝管道⽐进⼝管到底 3m,排⽓速度366 m ?s 1。
透平机产⽣的轴功为 703.2kW , 热损失为1.055 X 105kJ ? h -1。
乏⽓中的⼀⼩部分经节流阀降压⾄⼤⽓压⼒,节流阀前后的流速变化可忽略不计。
式计算经节流后⽔蒸⽓的温度及其过热度。
1 2解:稳态流动体系能量衡算⽅程: H u 2 g.lZ =W sQ2以每⼩时单位⽔蒸⽓作为计算标准51.055 10 454012 12 21223u (U 2 -⼭)(366 -61 ) 10 =65.117kJ kg2 2 2Z p ⼆ g Z =9.8 (-3) 10^ = -29.4 10‘kJ kg将上述结果代⼊能量衡算⽅程得到: H - -645.93kJ kg 查表得到4.482MPa , 728K 过热⽔蒸汽焓值: H^3340kJ kg 进出⼝焓变为出⼝⽓体焓值减去进⼝⽓体焓值::H =H 2 - ⽐对于节流膨胀过程,节流膨胀过程为等焓过程,汨'=0--23.24kJ kg 703.2 36004540 =-557.6kJ kg节流后⽔蒸⽓焓值:H 2=⽐:H = 3340 -646 = 2694kJ kg J内插法查0.1MPa 下过热⽔蒸汽表,得到: T =106.5 C ,过热度65C4 — 16 1mol 理想⽓体,400K 下在⽓缸内进⾏恒温不可逆压缩,由 0.1013MPa 压缩到1.013MPa 。
化工热力学课后答案(填空、判断、画图)第1章 绪言一、是否题1. 封闭体系的体积为一常数。
(错)2. 封闭体系中有两个相βα,。
在尚未达到平衡时,βα,两个相都是均相敞开体系;达到平衡时,则βα,两个相都等价于均相封闭体系。
(对)3. 理想气体的焓和热容仅是温度的函数。
(对)4. 理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5. 封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的⎰=21T T V dT C U ∆;同样,对于初、终态压力相等的过程有⎰=21T T P dT C H ∆。
(对。
状态函数的变化仅决定于初、终态与途径无关。
)二、填空题1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。
2. 封闭体系中,温度是T 的1mol 理想气体从(P i ,V i )等温可逆地膨胀到(P f ,V f ),则所做的功为()f i rev V V RT W ln =(以V 表示)或()i f rev P P RT W ln = (以P 表示)。
3. 封闭体系中的1mol 理想气体(已知igP C ),按下列途径由T 1、P 1和V 1可逆地变化至P 2,则A 等容过程的 W = 0 ,Q =()1121T P P R C igP ⎪⎪⎭⎫ ⎝⎛--,U =()1121T PPR C igP ⎪⎪⎭⎫⎝⎛--,H =1121T P P C ig P ⎪⎪⎭⎫ ⎝⎛-。
B 等温过程的 W =21lnP P RT -,Q =21ln P PRT ,U = 0 ,H = 0 。
第2章P-V-T关系和状态方程一、是否题1. 纯物质由蒸汽变成液体,必须经过冷凝的相变化过程。
(错。
可以通过超临界流体区。
)2. 当压力大于临界压力时,纯物质就以液态存在。
(错。
若温度也大于临界温度时,则是超临界流体。
化工热力学课后答案(填空、判断、画图)第1章 绪言一、是否题1. 封闭体系的体积为一常数。
(错)2.封闭体系中有两个相βα,。
在尚未达到平衡时,βα,两个相都是均相敞开体系;达到平衡时,则βα,两个相都等价于均相封闭体系。
(对)3. 理想气体的焓和热容仅是温度的函数。
(对)4.理想气体的熵和吉氏函数仅是温度的函数。
(错。
还与压力或摩尔体积有关。
)5.封闭体系的1mol 气体进行了某一过程,其体积总是变化着的,但是初态和终态的体积相等,初态和终态的温度分别为T 1和T 2,则该过程的;同样,对于初、终态压力相等的过程有。
(对。
状态函数的变化仅决定于初、终态与途径无关。
)二、填空题1. 状态函数的特点是:状态函数的变化与途径无关,仅决定于初、终态 。
2.封闭体系中,温度是T 的1mol 理想气体从(P i ,V i )等温可逆地膨胀到(P f ,V f ),则所做的功为()f i rev V V RT W ln =(以V 表示)或()i f rev P P RT W ln =(以P 表示)。
3.封闭体系中的1mol 理想气体(已知ig P C ),按下列途径由T 1、P 1和V 1可逆地变化至P 2,则A 等容过程的W= 0 ,Q=,U=,H= 。
B 等温过程的W=,Q=,U= 0 ,H= 0 。
第2章P-V-T关系和状态方程一、是否题1.纯物质由蒸汽变成液体,必须经过冷凝的相变化过程。
(错。
可以通过超临界流体区。
)2.当压力大于临界压力时,纯物质就以液态存在。
(错。
若温度也大于临界温度时,则是超临界流体。
)3.由于分子间相互作用力的存在,实际气体的摩尔体积一定小于同温同压下的理想气体的摩尔体积,所以,理想气体的压缩因子Z=1,实际气体的压缩因子Z<1。
(错。
如温度大于Boyle温度时,Z>1。
)4.纯物质的三相点随着所处的压力或温度的不同而改变。
(错。
纯物质的三相平衡时,体系自由度是零,体系的状态已经确定。
§4.1均相敞开系统的热力学基本关系 4.1.1均相纯物质或定组成体系 4.1.2均相敞开系统5. 下列各式中,化学位的定义式是( )。
A. ()in nS P i i n nH ,,⎥⎦⎤⎢⎣⎡∂∂=μ B.()in nS nV i i n nG ,,⎥⎦⎤⎢⎣⎡∂∂=μ C.()inT P i i n nA ,,⎥⎦⎤⎢⎣⎡∂∂=μ D.()innS T i i n nU ,,⎥⎦⎤⎢⎣⎡∂∂=μ6. 关于化学势的下列说法中不正确的是( )。
A. 系统的偏摩尔量就是化学势B. 化学势是系统的强度性质C. 系统中的任一物质都有化学势D. 化学势大小决定物质迁移的方向 3. 在373.15K 和2atm 下水的化学位与水蒸气化学位的关系为( )。
A. μ(水)=μ(汽) B. μ(汽)>μ(水) C. μ(水)>μ(汽) D. 无法确定 4.1.3相平衡准则和相律§4.2偏摩尔性质 4.2.1iM 的引入及定义一、判断题3. 只要温度、压力一定,任何偏摩尔性质总是等于化学位。
( )9. 偏摩尔体积的定义可表示为ix T i i n T i i c V n nV V ≠≠⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂=}{,P ,}{,P ,。
( ) 5. 只有偏摩尔自由焓与化学位相等,所以 i n P T i i j n nG ≠⎥⎦⎤⎢⎣⎡∂∂=,,)(μ是最有用的。
( ) 12. 在常温、常压下,将10cm 3的液体水与20cm 3的液体甲醇混合后,其总体积为30 cm 3。
( ) 二、选择题2. 下列偏摩尔自由焓表达式中,错误的为( )。
i iA. G =μB.i i i dG =Vdp-S dT()j i i T,P,n C. G nG /n i≠=∂∂⎡⎤⎣⎦()j i i T,nv,n D. G nG /n i≠=∂∂⎡⎤⎣⎦5. 下列化学位μi 和偏摩尔性质关系式正确的是( )。
习 题 一、是否题1、偏摩尔体积的定义可表示为{}{}ii x P T i n P T i i x V n nV V ≠≠⎪⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂=,,,,∂。
(错。
因对于一个均相敞开系统,n 是一个变数,即(){}0,,≠∂∂≠in P T i n n )2、对于理想溶液,所有的混合过程性质变化均为零。
(错。
V ,H ,U ,C P ,C V 的混合过程性质变化等于零,对S ,G ,A 则不等于零)3、对于理想溶液所有的超额性质均为零。
(对。
因is E M M M -=)2、体系混合过程的性质变化与该体系相应的超额性质是相同的。
(错。
同于4)5、理想气体有f=P ,而理想溶液有i i ϕϕ=ˆ。
(对。
因i i i i i i is iis i Pf Px x f Px f ϕϕ====ˆˆ)2、温度和压力相同的两种理想气体混合后,则温度和压力不变,总体积为原来两气体体积之和,总热力学能为原两气体热力学能之和,总熵为原来两气体熵之和。
(错。
总熵不等于原来两气体的熵之和) 3、因为G E (或活度系数)模型是温度和组成的函数,故理论上i γ与压力无关.(错。
理论上是T ,P ,组成的函数。
只有对低压下的液体,才近似为T 和组成的函数) 4、纯流体的汽液平衡准则为f v =f l 。
(对)5、混合物体系达到汽液平衡时,总是有l i v i l v l i v i f f f f f f ===,,ˆˆ。
(错。
两相中组分的逸度、总体逸度均不一定相等)理想溶液一定符合Lewis-Randall 规则和Henry 规则。
(对。
) 二、选择题1、由混合物的逸度的表达式i ig i i f RT G G ˆln +=知,igi G 的状态为 (A ,()1,ˆln ),(),,(00==+=P f f f RT P T G x P T G ig i ig i i ig i i i 因为) A 系统温度,P =1的纯组分i 的理想气体状态B 系统温度,系统压力的纯组分i 的理想气体状态C 系统温度,P =1,的纯组分iD 系统温度,系统压力,系统组成的温度的理想混合物 2、已知某二体系的212121211221A x A x A A x x RT G E+=则对称归一化的活度系数1ln γ是(A ) A 222111222112⎪⎪⎭⎫⎝⎛+xA x A x A AB 222111211221⎪⎪⎭⎫ ⎝⎛+x A x A x A AC212112x A AD 221221x A A三、填空题 1、填表偏摩尔性质(M i ) 溶液性质(M ) 关系式(iiM x M ∑=)()ii x f ˆlnln f()iiix f x f ˆln ln ∑=i ϕˆln lniix ϕϕˆln ln ∑=ln iRTG EiiE x RT G γln ∑=2、有人提出了一定温度下二元液体混合物的偏摩尔体积的模型是)1(),1(122211bx V V ax V V +=+=,其中V 1,V 2为纯组分的摩尔体积,a ,b 为常数,问所提出的模型是否有问题?由Gibbs-Duhem 方程得,b V x V x a 1122=, a,b 不可能是常数,故提出的模型有问题;若模型改为)1(),1(21222211bx V V ax V V +=+=,情况又如何?由Gibbs-Duhem 方程得,b V V a 12=,故提出的模型有一定的合理性_。
3、常温、常压条件下二元液相体系的溶剂组分的活度系数为32221ln x x βαγ+=(βα,是常数),则溶质组分的活度系数表达式是=2ln γ3121232x x ββα-+。
解: 由0ln ln 2211=+γγd x d x ,得()()[]121122222122121233232ln ln dx x x dx x x x x dx dx d x x d ββαβαγγ++=+-=⎪⎪⎭⎫ ⎝⎛-= 四、计算题1、298.15K , 若干NaCl(B)溶解于1kg 水(A)中形成的溶液的总体积的关系为 :(cm 3)。
求n B =0.5mol 时,水和NaCl 的偏摩尔体积。
解:当nB=0.5mol 时,18.62cm 3·mol -1且,V t =1010.35cm3 由于,mol 所以,2、用PR 方程计算2026.5kPa 和344.05K 的下列丙烯(1)-异丁烷(2)体系的摩尔体积、组分逸度和总逸度。
(a )5.01=x 的液相;(b )6553.01=y 的气相。
(设012=k )解:本题属于均相性质计算。
其中,组分逸度系数和组分逸度属于敞开系统的性质,而混合物的逸度系数和逸度属于封闭系统的性质采用状态方程模型,需要输入纯组分的i ci ci P T ω,,,以确定PR 方程常数,从附表查得各组分的i ci ci P T ω,,并列于下表丙烯和异丁烷的i ci ci P T ω,,组分,ici T /K ci P /MPai ω丙烯(1) 304.19 7.381 0.225异丁烷(2) 425.18 3.797 0.193对于二元均相混合物,若给定了温度、压力和组成三个独立变量,系统的状态就确定下来了,并可以确定体系的状态为气相。
另外,对于混合物,还需要二元相互作用参数,已知012=k 。
计算过程是()2,1,=i b a i i →b a ,→V →()ϕϕln ;2,1ˆln =i i →()()ϕϕP f x P f i i i ln ln ,ˆln ˆln ==用软件来计算。
启动软件后,输入i ci ci P T ω,,和独立变量,即能方便地得到结果,并可演示计算过程。
3、常压下的三元气体混合物的32312115.03.02.0ln y y y y yy +-=ϕ,求等摩尔混合物的321ˆ,ˆ,ˆf f f 。
解:(){}()3132221323121,,113.025.02.015.03.02.0ln ˆln 3,2y y y y y dn n n n n n n n n n d n n n P T +-=+-=⎥⎦⎤⎢⎣⎡∂∂=≠ϕϕ同样得233121215.065.02.0ˆln y y y y ++=ϕ 222121315.025.03.0ˆln y y y y ++=ϕ组分逸度分别是()511.10ˆln ˆln 111==ϕPy f同样得()538.10ˆln ˆln 222==ϕPy f()505.10ˆln ˆln 223==ϕPy f4、三元混合物的各组分摩尔分数分别0.25,0.3和0.45,在6.585MPa 和348K 下的各组分的逸度系数分别是0.72,0.65和0.91,求混合物的逸度。
解:254.091.0ln 45.065.0ln 3.072.0ln 25.0ˆln ln -=++==∑i i y ϕϕ()631.1)254.0(585.6ln ln ln =-+==ϕP f5、 )MPa (109.5=f 利用Wilson 方程,计算下列甲醇(1)-水(2)体系的组分逸度(a )P =101325Pa ,T =81.48℃,y 1=0.582的气相;(b )P =101325Pa ,T =81.48℃,x 1=0.2的液相。
已知液相符合Wilson 方程,其模型参数是11598.1,43738.02112==ΛΛ解:本题是分别计算两个二元混合物的均相性质。
给定了温度、压力和组成三个独立变量, 均相混合物的性质就确定下来了。
(a )由于系统的压力较低,故汽相可以作理想气体处理,得971.58582.0325.101ˆ11=⨯==Py f v (kPa )()354.42582.01325.101ˆ22=-⨯==Py f v (kPa )理想气体混合物的逸度等于其总压,即325.101==P f v(kPa )[也能由其它方法计算]。
(b )液相是非理想溶液,组分逸度可以从活度系数计算,根据系统的特点,应选用对称归一化的活度系数,ii l i l i x f f γ=ˆ由于 ()()()()si sv s i sv i sl i s i l i l i l i P P T f T f P T f P T f f ≈==≈≈=ϕ,,所以ii s i l i x P f γ≈ˆ其中,蒸汽压si P 由 Antoine 方程计算,查附表得纯物质的Antoine 常数,并与计算的蒸汽压同列于下表甲醇和水的Antoine 常数和蒸汽压组分(i )i A i B i CMPa /15.27348.81exp ⎪⎪⎭⎫ ⎝⎛++-=i ii s i CB A P甲醇(1) 9.4138 3477.90 -40.53 0.190水(2)9.3876 3826.36 -45.47 0.0503活度系数i γ由Wilson 模型计算,由于给定了Wilson 模型参数11598.1,43738.02112==ΛΛ,计算二元系统在63.354=T K和418.01,582.0121=-==x x x时两组分的活度系数分别是()()07.10703.0045.1572.0418.0268.0ln ln 1121221212112221211==-+=⎥⎦⎤⎢⎣⎡Λ+Λ-Λ+Λ+Λ+-=γγx x x x x x x 和()()23.1210.0572.0045.1582.00653.0ln ln 2212112121221112122==-⨯+-=⎥⎦⎤⎢⎣⎡Λ+Λ-Λ+Λ+Λ+-=γγx x x x x x x所以,液相的组分逸度分别是118.0ˆ1111==x P f s l γ(MPa)0259.0ˆ2222==x P f s l γ(MPa)液相的总逸度为091.2418.00259.0ln 418.0582.0118.0ln582.0ˆlnln 1-=+==∑=Ni ili i l x f x f124.0=l f (MPa )6、已知环己烷(1)-苯(2)体系在40℃时的超额吉氏函数是21458.0x x RTG E=和3.24,6.2421==s s P P kPa ,求(a )f f f l l ,ˆ,ˆ,,2121γγ;(b )1,22,1,H H ;(c)*2*1,γγ。
解:(a )由于iγln 是RTG E的偏摩尔性质,由偏摩尔性质的定义知()22,,11458.0ln 2x n RT nG n P T E=⎥⎥⎦⎤⎢⎢⎣⎡∂∂=γ同样得到 212458.0ln x =γ(b ) 22458.0111111116.24ˆx s l l e x x P x f f =≈=γγ 同样得21458.0222222223.24ˆx s l l e x x P x f f =≈=γγ *112,1γf H =同理*221,2γf H=由(c )的计算结果可得1,22,1H H 和 (c)由 ()∞→∞-=-=i x i i i i i γγγγγln lim ln ln ln ln 0*得到*ln i γ7、)1(458.0ln 22*1-=x γ)1(458.0ln 21*2-=x γ已知苯(1)-环己烷(2)液体混合物在303K 和101.3kPa 下的摩尔体积是21164.28.164.109x x V --=(cm 3 mol -1),试求此条件下的(a )21,V V ;(b)V∆;(c)*,E E V V (不对称归一化)。