Matlab程序设计(2016大作业)

五邑大学《MATLAB程序设计》选修课大作业学生姓名：学生学号：学院年级专业：学院级专业指导老师：刘战（副教授）成绩：2010年12月1、求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧-=+-+-=-+-=++-=--+81025695832475412743w z y x w z x w z y x w z y x 求系数矩阵的秩；求出方程组的解。

解：在MATLAB 中输入以下指令：>> a=[3 4 -7 -12;5 -7 4 2;1 0 8 -5;-6 5 -2 10]a =3 4 -7 -125 -7 4 21 0 8 -5-6 5 -2 10>> rank(a)ans =4>> b=[4;-3;9;-8]b =4-39-8>> k=a\bk =-1.4841-0.68160.5337-1.2429故系数矩阵的秩为4 方程组的解为x=-1.4841 y=-0.6816 z=0.5337 w=-1.24292、设))]1/()sin 3((5.0cos[2x x y ++=把x=0~2π间分为101点，画出以x 为横坐标，y 为纵坐标的曲线；解：在MATLAB 中输入以下指令：x=linspace(0,2*pi,101);y=cos(0.5+3.*sin(x)./(1+x.^2));plot(x,y,'g-') //这里可以把‘g-’改成其它的，具体请对表基本线型和颜色(见附录) title('函数曲线')xlabel('自变量 x')ylabel('因变量y')text(2,0.5,'y=cos[0.5+3sin(x)/(1+x^2)]')grid //这里可以不用grid 也就是没有栅格 用就有 下图就没用输入结果为：3、设6234)(245+-+-=x x x x x f（1）取x=[-2,8]之间函数的值（取100个点），画出曲线，看它有几个零点。

1.设计一个程序，要求用户用键盘输入10次，输入内容可以是数字、英文、汉字、或者
其他文字或者符号。

如果输入的是数字，则把存入一个数字数组当中；如果输入的是英文的字符，则存入一个英文字符数组当中；如果是其他字符，则存入一个字符串数组中。

当10次内容都输入完毕后，先输出英文数组中的内容，然后输出字符串数组中的内容。

如果数字数组中元素数量大于3个，则由数字数组中的数字组成一个a0 X n+a1X n-1+………an=f（X），其中a0…an是数组中第一到最后一个元素，n为元素的个数，并且画出这个函数在区间[0,20]之间的曲线。

如果数字数组中的元素数量小于等于3个，则由数字数组中的数字组成一个a0 X n+a1Y n-1+anZ=0的方程，并且画出这个函数在[0,10]之间的曲线。

具体要求：
（1）画出程序的结构图
（2）画出程序的流程图
（3）每一行或者每一小段都需要标注
（4）附上完整的程序
2.按如下条件，设计一个完整的程序。

（1）有一片草原，草原上有人、狼、羊、鸡和蝗虫生活；
（2）被吃过的草，三年之后可以修复；
（3）一个人一年吃一只羊，10个人一年杀一只狼，一个人一年吃一只鸡；
（4）一头狼一年吃一只羊，一头狼三年成活一个幼崽；
（5）一只羊一年吃掉100平方米的草原；
（6）一只鸡一年吃掉1000只蝗虫；
（7）一只蝗虫一年吃掉一平方米的草原。

按如上条件，模拟出草原及其上述的生物从现在起500年间的状态。

具体要求：
（1）写出具体的解题思路
（2）列出详细的变量表，写出每一个变量的含义
（3）写出完整的程序，最好有图。

Matlab的基本操作一、使用函数实现对下列矩阵的左旋和右旋以及反转已知答案：如图：矩阵如图矩阵的左旋如图一矩阵的右旋如图二矩阵的左右反转如图三矩阵的上下反转如图四二、已知A=[8 9 5 ] B=[-1 3 -2][36 -7 11] [2 0 3][21 -8 5] [-3 1 9 ]计算：1)A+5*B;2)A*B和A.*B3)A^3和A.^34)A/B和B\A5)[A,B]答案：A=[8 9 5；36 -7 11；21 -8 5];B=[-1 3 -2；2 0 3；-3 1 9];A+5*BA*BA.*BA^3A.^3A/BA\B[A,B]程序运行结果如下：第二章、Matlab程序设计一、已知S=1+2+22+23+…+263求S的值答案：代码如下：ClearClcs=0,j=2for i=1:63s=s+j^iends程序运行结果如下：二、第三章、Matlab绘图一、在同一坐标系中画出下列函数的图像：x2，-x2，xsin（x）在[0,2π]上的函数图像程序代码如下：clearclcx=0:pi/100:2*pi;y1=x.^2;y2=-x.^2;y3=x.*sin(x);title('同一坐标下的函数图像')plot(x,y1,':',x,y2,'h',x,y3,'--')程序运行结果如下：二、绘制极坐标图像：程序代码如下：clearclcx=0:0.01:2*pi;y=2*cos(2*(x-pi/8));title('极坐标图像')xlabel('x')ylabel('y')polar(x,y)程序运行结果如下：第四章、Matlab符号运算一、求函数y=e-x2 的傅立叶变换及其逆变换程序代码如下：clearclcsyms x t;y=exp(-x^2);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)程序运行结果如下：二、求下列极限值：答案：1、程序代码：clearclcsyms x;s1=sin(2*x)/sin(5*x);limit(s1,x,0)s2=(1+1/x)^(2*x);limit(s2,x,inf)程序运行结果如下：第五章、Matlab数值运算一、建立一个3*4阶随机矩阵，求矩阵的最大值、最小值、方差和标准差、极差、协方差，和自相关阵程序代码如下：clearclcA=rand(3,4)B=var(A)C=std(A)D=range(A)E=cov(A)F=corrcoef(A)程序运行结果如下：二、求函数f（x）=x3-2x+1在x=[-1 1]之间的极小值和x=-1附近的零点程序代码如下：clearclc[x,y]=fminbnd('x.^3-2.*x+1',-1,1)[x,y]=fzero('x.^3-2.*x+1',-1)程序运行结果如下：第六章、Matlab图形用户界面一、建立一个具有三个输入框的窗口对话框程序代码如下：clearclcprompt={'姓名','年龄','班级'}；DTitle='注册学生信息';line[1;1;1];def{'乔阳'，'18','100412105'};info=inputdlg(prompt,DTitle,line,def,'ON')程序运行结果如下：二、设计一个表现下载进度的进度条程序代码如下：clearclch = waitbar(0,'正在下载，请稍等……');for i=1:1000waitbar(i/10000,h)endclose(h)程序运行结果如下：第七章、Matlab Simulink 仿真一、仿真信号x（t）=sin(t)sin(10t)的波形仿真步骤：1.建立模型窗口：生成无标题（intitled）的模型窗口；2.添加信号源模块（sine）、输出模块（scope）、数学模块（Dot product）3.设置模块参数：如下图：4.编辑模块即将各个模块连接起来。

matlab大作业学号姓名：年级：专业：1、产生一个10 10的随机矩阵A，要求A中元素均为整数，范围[1,50]。

1)求出A中所有元素之和S，平均值M。

2)找到所有小于平均值，且能被3整除的元素。

3)绘制出A的二维纵向柱状图，横坐标为[8 5 9 1 2 3 4 7 10 13],条形宽度为0.7的“stacked”样式。

代码如下：clc,clear all,close allA=round(rand(10,10)*50);disp(A)S=sum(sum(A));P=mean(mean(A));disp(S)disp(P)disp('所有小于平均数且能被三整除的元素')XPS=H((mod(H,3)==0)&(H<P));disp(XPS')subplot(1,1,1),bar(A,0.7,'stacked'),title('ygh');set(gca,'XTickLabel',{'8','5','9','1','2','3','4','7','10','13'})2、产生一个随机四位密码。

用户用“input”进行输入对比。

猜错提示“WRONG”，正确提示“RIGHT”同时退出程序，最多五次机会。

代码如下：clc,clear all,close alldisp('请输入密码')A=round(8999*rand(1,1))+1000;m=1;while m<=5N=input('请输入一个四位数：');if A==N;disp('RIGHT');breakelsedisp('WRONG');endm=m+1;enddisp('密码是：')disp(A)disp('输入结束')3、按照脚本文件的编程风格，用for和while循环嵌套输出如下的乘法口诀表。

matlab课程设计大作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及MATLAB 在工程计算和数据分析中的应用。

通过本课程的学习，学生将能够熟练使用MATLAB进行简单数学计算、线性方程组求解、函数图像绘制等。

1.掌握MATLAB基本语法和编程结构。

2.了解MATLAB在工程计算和数据分析中的应用。

3.熟悉MATLAB的函数库和工具箱。

4.能够使用MATLAB进行简单数学计算。

5.能够使用MATLAB求解线性方程组。

6.能够使用MATLAB绘制函数图像。

7.能够利用MATLAB进行数据分析和处理。

情感态度价值观目标：1.培养学生对计算机辅助设计的兴趣和认识。

2.培养学生团队合作和自主学习的能力。

二、教学内容本课程的教学内容主要包括MATLAB基本语法、编程技巧以及MATLAB在工程计算和数据分析中的应用。

1.MATLAB基本语法：介绍MATLAB的工作环境、基本数据类型、运算符、编程结构等。

2.MATLAB编程技巧：讲解MATLAB的函数调用、脚本编写、函数文件编写等编程技巧。

3.MATLAB在工程计算中的应用：介绍MATLAB在数值计算、线性方程组求解、图像处理等方面的应用。

4.MATLAB在数据分析中的应用：讲解MATLAB在数据采集、数据分析、数据可视化等方面的应用。

三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合的方式进行教学。

1.讲授法：通过讲解MATLAB的基本语法、编程技巧以及应用案例，使学生掌握MATLAB的基本知识和技能。

2.案例分析法：通过分析实际工程案例，使学生了解MATLAB在工程计算和数据分析中的应用。

3.实验法：安排上机实验，使学生在实际操作中巩固所学知识，提高实际编程能力。

四、教学资源本课程的教学资源包括教材、实验设备、多媒体资料等。

1.教材：选用《MATLAB教程》作为主要教材，辅助以相关参考书籍。

2.实验设备：为学生提供计算机实验室，配备有MATLAB软件的计算机。

m a t l a b综合大作业(附详细答案)-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1．数组的创建和访问（20分，每小题2分）：1)利用randn函数生成均值为1，方差为4的5*5矩阵A；实验程序：A=1+sqrt(4)*randn(5)实验结果：A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B；实验程序：B=A(:)实验结果：B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C；实验程序：C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果：C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素；]实验程序：G=A(find(A>0))实验结果：G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D；实验程序：D=A'实验结果：D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E；实验程序：E=flipud(fliplr(A))实验结果：E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F；实验程序：F=A;F(:,[2,4])=[]实验结果：F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量；实验程序：[Av,Ad]=eig(A)实验结果：特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值；实验程序：lieSUM=sum(A)实验结果：lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值；实验程序：average=mean(A)实验结果：average =-0.1326 2.1378 1.7990 1.1248 1.24172．符号计算（10分，每小题5分）：1)求方程组20,0++=++=关于,y z的解；uy vz w y z w实验程序：S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果：y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解； 实验程序：[x,y]=dsolve('Dx=y','Dy=-x')实验结果：x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3．数据和函数的可视化（20分，每小题5分）：1)二维图形绘制：绘制方程2222125x y a a +=-表示的一组椭圆，其中0.5:0.5:4.5a =；实验程序：t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果：2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线；实验程序：x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果：3)用曲面图表示函数22z x y =+；实验程序：x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果：4)用stem 函数绘制对函数cos 4y t π=的采样序列；实验程序：t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果：4. 设采样频率为Fs = 1000 Hz ，已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=，由于某一原因，原始信号被白噪声污染，实际获得的信号为))((ˆt size randn x x+=，要求设计出一个FIR 滤波器恢复出原始信号。

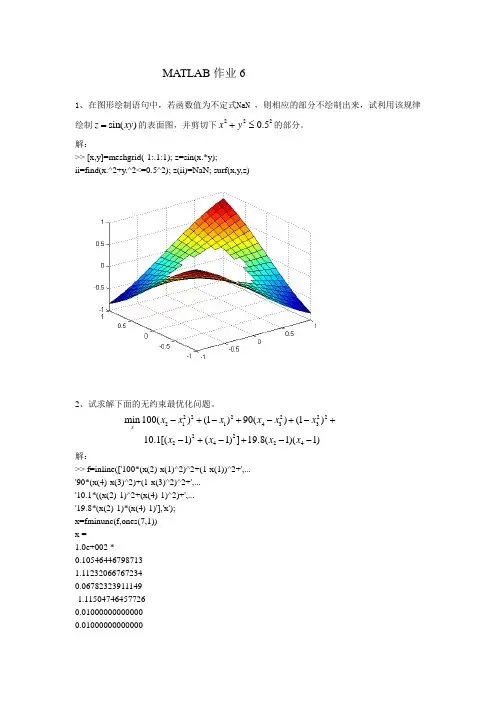
MATLAB 作业61、在图形绘制语句中，若函数值为不定式NaN ，则相应的部分不绘制出来，试利用该规律绘制sin()z xy =的表面图，并剪切下2220.5x y +≤的部分。

解：>> [x,y]=meshgrid(-1:.1:1); z=sin(x.*y);ii=find(x.^2+y.^2<=0.5^2); z(ii)=NaN; surf(x,y,z)2、试求解下面的无约束最优化问题。

222222211433222424min 100()(1)90()(1)10.1[(1)(1)]19.8(1)(1)xx x x x x x x x x x -+-+-+-+-+-+--解：>> f=inline(['100*(x(2)-x(1)^2)^2+(1-x(1))^2+',...'90*(x(4)-x(3)^2)+(1-x(3)^2)^2+',...'10.1*((x(2)-1)^2+(x(4)-1)^2)+',...'19.8*(x(2)-1)*(x(4)-1)'],'x');x=fminunc(f,ones(7,1))x =1.0e+002 *0.105464467987131.112320667672340.06782323911149-1.115047464577260.010000000000000.010000000000000.010000000000003、 试用图解法求解下面的非线性规划问题，并用数值求解算法验证结果。

321211221212min (44)20..100,0x x x x x s t x x x x +-+-+≥⎧⎪-+-≥⎨⎪≥≥⎩ 解：>> [x1,x2]=meshgrid(0:0.02:1,1:0.02:2);z=x1.^3+x2.^2+4*x1+4;ii=find(x1-x2+2<0); z(ii)=NaN;ii=find(-x1.^2+x2-1<0); z(ii)=NaN;ii=find(x1<0); z(ii)=NaN; ii=find(x2<0); z(ii)=NaN;surf(x1,x2,z)function [c,ce]=exc6f4(x)ce=[];c=[x(1)^2-x(2)+1];>> f_opt=inline('x(1)^3+x(2)^2+4*x(1)+4','x');A=[-1 1]; B=2; Aeq=[]; Beq=[]; xm=[0;0];x=fmincon(f_opt,[0;1],A,B,Aeq,Beq,xm,[],'exc6f4');4、 试求解此线性规划问题：6712341236723571,2,,7min 421..390x x x x x x x x x x x s t x x x x x ++++=⎧⎪-+--+=⎪⎨+++=⎪⎪≥⎩解：>> [x1,x2]=meshgrid(0:0.02:1,1:0.02:2);z=x1.^3+x2.^2+4*x1+4;ii=find(x1-x2+2<0); z(ii)=NaN;ii=find(-x1.^2+x2-1<0); z(ii)=NaN;ii=find(x1<0); z(ii)=NaN; ii=find(x2<0); z(ii)=NaN;surf(x1,x2,z)function [c,ce]=exc6f4(x)ce=[];c=[x(1)^2-x(2)+1];>> f_opt=inline('x(1)^3+x(2)^2+4*x(1)+4','x');A=[-1 1]; B=2; Aeq=[]; Beq=[]; xm=[0;0];x=fmincon(f_opt,[0;1],A,B,Aeq,Beq,xm,[],'exc6f4');5、 试求解下面的二次型规划问题，并用图示的形式解释结果。

2012年12月7日星期五第2章 MATLAB 矩阵运算基础2.1 在MATLAB 中如何建立矩阵，并将其赋予变量a ？⎥⎦⎤⎢⎣⎡194375>> a=[5 7 3;4 9 1]2.2 有几种建立矩阵的方法？各有什么优点？可以用四种方法建立矩阵：①直接输入法，如a=[2 5 7 3]，优点是输入方法方便简捷；②通过M 文件建立矩阵，该方法适用于建立尺寸较大的矩阵，并且易于修改；③由函数建立，如y=sin(x)，可以由MATLAB 的内部函数建立一些特殊矩阵；④通过数据文件建立，该方法可以调用由其他软件产生数据。

2.3 在进行算术运算时，数组运算和矩阵运算各有什么要求？进行数组运算的两个数组必须有相同的尺寸。

进行矩阵运算的两个矩阵必须满足矩阵运算规则，如矩阵a 与b 相乘（a*b ）时必须满足a 的列数等于b 的行数。

2.4 数组运算和矩阵运算的运算符有什么区别？在加、减运算时数组运算与矩阵运算的运算符相同，乘、除和乘方运算时，在矩阵运算的运算符前加一个点即为数组运算，如a*b 为矩阵乘，a.*b 为数组乘。

2.5 计算矩阵与之和。

⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242>> a=[5 3 5;3 7 4;7 9 8];>> b=[2 4 2;6 7 9;8 3 6];>> a+bans =777914131512142.6 求的共轭转置。

⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x >> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i];>> x’4.0000 - 8.0000i 3.0000 - 2.0000i 3.0000 -5.0000i 7.0000 +6.0000i 2.0000 +7.0000i 9.0000 - 4.0000i 1.0000 - 4.0000i 3.0000 + 9.0000i 7.0000 + 5.0000i 4.0000 - 4.0000i 2.7 计算与的数组乘积。

matlab 期末大作业（30分，每题6分）1. 积分运算（第四数值和五章符号）(1)定积分运算：分别采用数值法（quad ，dblquad ）和符号运算（syms, int ）一重定积分π⎰1. 数值法（quad ）a) 运行代码：b) 运行结果：2. 符号运算（syms ）a) 运行代码：b) 运行结果：二重定积分112200()x y dxdy+⎰⎰1.数值法（dblquad）：a)运行代码：b)运行结果：2.符号运算（syms）：a)运行代码：b)运行结果：(2) 不定积分运算sin dxdy ⎰⎰（(x/a)+b/y） i.运行代码：ii.运行结果：2. 用符号法和数值法求解线性代数方程 （第五章和第二章）⎩⎨⎧=+=+12*22x *213*12x *a11y a a y a （1） 用syms 定义待解符号变量x,y 和符号参数a11,a12,a21,a22，用符号solve 求x,y 通解 1. 运行代码：2. 运行结果：（2） 用subs 带入a11=2,a12=4,a21=6,a22=8,求x 和y 特解，用vpa 输出有效数值4位的结果 1. 运行代码：2. 运行结果：（3） 采用左除(\)和逆乘法求解符号参数赋值后的方程 ⎩⎨⎧=+=+12*8x *63*4x *2y y1. 运行代码：2. 运行结果：3.数值法和符号法求解非线性方程组(第四数值和五章符号 )（1）采用数值法（fsolve ）求解初始估计值为x0 = [-5; -5]的数值解1. 运行代码：2. 运行结果：21x 21x 21e x 2x e x x 2--=+-=-（2）符号法（solve ）的符号结果用eval 或double 转化为数值结果.1. 运行代码：2. 运行结果：4. 解二阶微分方程 (第四数值和五章符号 )⎪⎩⎪⎨⎧===++6)0(',0)0(09322y y y dx dy dx y d（1）数值ode 求特解，用plot (x,y) 画t 在[0,10]范围内（x ，y ）数值曲线 1. 运行代码：2. 运行结果：（2）符号运算dsolve求通解，用ezplot画t在[0,10]范围内（x，y）符号曲线1. 运行代码：2. 运行结果：5. 三维绘图（第六章）已知：x和y都在[-8,8]范围内，采用subplot(3,1,x)绘制三个子图，它们分别是用meshgrid和mesh绘制网格图、用c=contour 绘制等位线和用surf 绘制曲面图1.运行代码：2.运行结果：。

MATLAB程序设计期末大作业姓名：班级：学号：指导教师：题目1给定如图1所示的单位负反馈系统。

图1在系统中分别引入不同的非线性环节（饱和、死区、与滞环），观察系统的阶跃响应，并且分析比较不同的非线性环节对系统性能的影响。

解：1、利用MATLAB中的simulink工具箱，对题设控制系统进行建模，如图1 所示。

则没有任何非线性环节的系统，其阶跃响应曲线如图2 所示。

图22、在系统中加入饱和非线性环节，系统框图如图3所示。

其中，饱和非线性环节的输出上限为0.1，输出下限为-0.1；阶跃信号幅值为1。

图3利用simulink进行仿真，得到的阶跃响应曲线如图4所示。

图4为了比较当饱和非线性环节输出上下限变化时系统阶跃响应的不同，可以利用simulink中的to workspace模块，将多次仿真的结果记录到工作空间的不同数组中，并且绘制到同一幅图像上。

此时，系统框图如图5所示。

图5将4种情况下系统的阶跃响应曲线绘制在同一幅图像中，代码如下：>> plot(tout,out2);>> plot(tout,out2);>> hold on;>> grid on;>> gtext('0.1');>> plot(tout,out1);>> plot(tout,out3);>> gtext('0.2');>> plot(tout,out4);>> gtext('0.5');运行程序，结果如图6所示。

图6从图6中可以看出：当饱和非线性环节的输出范围较窄时，系统的阶跃响应速度较慢，上升时间长；同时，超调量较小，振荡不明显;随着输出范围的扩大，系统的响应速度加快，上升时间大大减小，同时伴有显著的振荡。

这是因为饱和环节会对信号起到限幅作用；不难想象，限制作用越强，系统的输出越不容易超调，响应也会越慢，这从图6也可以看出这一趋势。

Matlab大作业大作业要求：1 以下matlab编程和simulink题目各选做一个，大作业总共两道题。

2如果不做给定的题目，自己选题，提前qq（244731524）上和我说下，根据题目的难易，可以考虑多给些时间。

3 第十周前由各班学委统一将纸质版交给我，写上班级，学号，姓名。

4 请勿抄袭。

Matlab编程1、使用m文件对周期信号频域进行分析(1)用matlab求周期矩形脉冲的傅里叶级数，并绘制出周期矩形脉冲信号及其频谱图(2)，用matlab求改变周期、脉冲宽度后的周期矩形脉冲的傅里叶级数和频谱，并分析周期，脉宽对周期信号频谱的影响。

2、使用m文件对非周期信号频域进行分析(1)用matlab对矩形脉冲信号的频谱进行分析(2)利用matalb函数绘制给定信号的幅度谱和相位谱。

Simulink1、使用Simulink的积分模块求解二阶微分方程：x’’+0.2x’+0.4x =0.2u(t) ，u (t) 是单位阶跃函数a、用积分模块创建求解微分方程的模型思路:利用连续系统模块库中的积分器Integrator，解微分方程。

建模仿真：阶跃信号Step ，求和sum,常数增益gain,积分器,示波器scopeb、用传递函数求微分方程思路:对微分方程作laplace变换，移项整理后求得传递函数，利用连续系统模块库中的传递函数模块Transfer Fcn ，解微分方程。

建模仿真：阶跃信号Step ，示波器scope，传递函数模块Transfer Fcn等2、使用simupower system模块求解电路。

电路如图所示，参数如下：R1=2，R2=4，R3=12，R4=4，R5=12，R6=4，R7=2，Us=10V。

求i3，U4，U7；。

一、大作业题目：
1、MATLAB在XXXXXX课程中的应用
比如在信号与系统、数字信号处理、自动控制原理、数据压缩等课程中的应用
2、SIMULINK在通信系统中的应用
3、GUI界面设计（可把绘图、程序设计结合起来）
4、实现一定的功能的程序
上述题目可任选一题做，也可自行选题做，希望大家通过做这次大作业，也能使自己有所提高，有所收获。

二、大作业要求交电子版和纸制版。

纸制版：大作业写成报告的形式，用A4纸打印，封面写上题目班级学号，报告里面必须包含设计思路，设计过程，设计结果。

（不参加检查答辩的同学的电子版交给学习委员或班长）
电子版：要求交源程序、报告电子版本。

（所有同学的电子版交给学习委员或班长）
三、18周交实验报告，18周检查大作业。

检查：要得优秀良好的同学必须检查答辩，但不是所有检查答辩的同学都一定能得到良好及以上的成绩。

Matlab程序设计课程大作业题目名称：_________________________________ 班级：_________________________________ 姓名：_________________________________ 学号：_________________________________ 课程教师：温海骏学期：2015-2016学年第2学期完成时间：MATLAB 优化应用§1 线性规划模型一、线性规划问题：问题1：生产计划问题假设某厂计划生产甲、乙两种产品，现库存主要材料有A 类3600公斤，B 类2000公斤，C 类3000公斤。

每件甲产品需用材料A 类9公斤，B 类4公斤，C 类3公斤。

每件乙产品，需用材料A 类4公斤，B 类5公斤，C 类10公斤。

甲单位产品的利润70元，乙单位产品的利润120元。

问如何安排生产，才能使该厂所获的利润最大。

问题2：投资问题某公司有一批资金用于4个工程项目的投资，其投资各项目时所得的净收益(投入资金百分比)如下表：工程项目收益表由于某种原因，决定用于项目A 的投资不大于其他各项投资之和而用于项目B 和C 的投资要大于项目D 的投资。

试确定该公司收益最大的投资分配方案。

问题3：运输问题有A 、B 、C 三个食品加工厂，负责供给甲、乙、丙、丁四个市场。

三个厂每天生产食品箱数上限如下表：四个市场每天的需求量如下表：从各厂运到各市场的运输费(元/每箱)由下表给出：求在基本满足供需平衡的约束条件下使总运输费用最小。

§2 多目标规划模型多目标规划定义为在一组约束下，多个不同的目标函数进行优化设计。

数学模型：12min ()()().()0,1,2,,m j f x f x f x st g x j k⎡⎤⎣⎦≤=其中x=(x 1 ,x 2 , … ,x n )为一个n 维向量；f i (x)为目标函数，i=1,2, … ,m; g j (x)为系统约束, j=1, 2, … ,k 。

MATLAB 大作业请各位同学，自己完成matlab 大作业的内容。

禁止相互抄袭，如有雷同，零分计算。

大作业的格式按照实验报告的格式书写，务必标明题号，作业完成后，将生成的报告打印出来提交。

正文的字号以宋体五号字，1.5倍行距的格式打印。

请与18周五前将大作业报告由班级负责人统一收齐交给我，过期不收。

1、 试编写名为test01.m 的MATLAB 函数，用以计算下述的值：⎪⎩⎪⎨⎧-<->=t t n t t t n t f 的对所有其他情况的对所有)4/sin()(si )4/sin()sin()4/sin()(si )4/sin()(ππππ要绘制t 关于函数f (t )的图形，其中t 的取值范围为ππ66≤≤-t ，间距为10/π。

（提示：注意要产生一系列的点，这里可考虑t 的输入是向量形式，可以利用find 函数找出所需限定值的元素的位置，对其按需要赋值后，再进行绘图；其次，另外一种思路，也可考虑使用循环的形式来实现）2、 编写函数，在同一窗口的4个子图中利用plot 等语句绘制y=at 2图像，其中a=[1 2 5 10],t错误！未找到引用源。

3、 求函数32)(3-+=x x x f 在区间[-5,5]上的最大值和最小值。

4、 求解函数⎰12dx e x 的数值积分和符号积分，并比较结果。

5、 求解微分方程3|;1|2)1(002='='=''+==x x y y y x y x 的精确解和解析解，并绘制图形。

假设求解区间为[0,10] 。

6、 说说你对MATLAB 及应用这门课程学习后的体会，另外请说明在所学章节中哪一章的内容你最感兴趣，为什么？哪一章的内容你认为是没有必要学习的，为什么？如果可以选择MATLAB 的学习的内容的话，谈谈你所期望学到的知识类别的前三种。

1.实验名称 MATLAB 大作业2.实验目的(1)理解Matlab数据对象的特点；(2)掌握基本Matlab运算规则；(3)掌握Matlab帮助的使用方法；3.实验设备及条件计算机一台（带有MATLAB7.0以上的软件环境）4.实验内容及要求请各位同学，自己完成matlab大作业的内容。

控制系统仿真大作业例题：中央空调控制系统的MA TLAB仿真运用PID算法，利用MATLAB仿真技术对经验法建立的中央空调控制系统模型进行仿真，通过Matlab仿真分析。

1、基于Matlab的变压器差动保护闭环仿真研究（潘高锋）应用Matlab建立微机保护仿真系统，并对不同原理的变压器差动保护进行仿真和比较。

仿真系统采用积木式结构，根据微机保护的实现原理构建模块，实现保护的闭环仿真，对保护的动作过程进行分析。

2、基于MATLAB/SIMULINK的交流电机调速系统建模与仿真（郝士杰）根据直接转矩控制原理，利用MATLAB/SIMULINK软件构造一个交流电机调速系统，，实现高效的调速系统设计。

利用MATLAB/SIMULINK仿真验证该方法的有效性。

3、基于Bode图的电液比例速度控制的设计（张坤玉）对电液比例速度控制系统进行建模分析，并利用Bode图对铣耳机组纵向进给装置电液比例速度控制系统的动态分析和计算机仿真。

设计校正装置使得系统满足① 频域指标:系统的幅角裕量r=72。

;开环穿越频率186rad/s;闭环频率-3dB处的频率是100rad/s;幅值裕量Kg>8dB。

② 时域指标:超调量<3%;上升时间tr=0.05s;调节时间t=0.25s.③ 静态指标:系统静态误差为零。

4、Matlab在动态电路分析中的应用（杨继陈）用Matlab计算动态电路，可得到解析解和波形图。

一阶电路先计算3要素，后合成解析结果；RLC串联和并联的二阶电路采用自编的通用函数计算，自编函数采用了Matlab求解微分方程的符号运算方法；一般的二阶电路和高阶电路采用拉氏变换列写电路方程，再用拉氏反变换得到解析结果.通过实例分析，分析Matlab在动态电路分析方面的优越性.5、大型天线指向控制系统的MA TLAB分析与仿真（杜涵潇）建立大型天线指向控制系统结构图，若要求系统斜披响应的稳态误差小于1%，阶跃响应的超调量小于5%，调节时间小于2s(△=2%)，要求：设计合适的校正网络，并绘制校正后系统的单位阶跃响应曲线；当输入为0时，分析扰动对系统输出的影响。

M A T L A B大作业(总15页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求：（1）编写程序并上机实现，提交作业文档，包括打印稿（不含源程序）和电子稿（包含源程序），以班为单位交，作业提交截止时间6月24日。

（2）作业文档内容：问题描述、问题求解算法（方案）、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。

打印稿不要求MATLAB程序，但电子稿要包含MATLAB程序。

（3）作业文档字数不限，但要求写实，写出自己的理解、收获和体会，有话则长，无话则短。

不要抄袭复制，可以参考网上、文献资料的内容，但要理解，要变成自己的语言，按自己的思路组织内容。

（4）从给出的问题中至少选择一题(多做不限，但必须独立完成，严禁抄袭)。

（5）大作业占过程考核的20%，从完成情况、工作量、作业文档方面评分。

第一类：绘制图形。

（B级）问题一：斐波那契（Fibonacci）螺旋线，也称黄金螺旋线（Golden spiral），是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线的图案，是自然界最完美的经典黄金比例。

斐波那契螺旋线，以斐波那契数为边的正方形拼成的长方形，然后在正方形里面画一个90度的扇形，连起来的弧线就是斐波那契螺旋线，如图所示。

问题二：绘制谢尔宾斯基三角形（Sierpinskitriangle）是一种分形，由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。

其生成过程为：取一个实心的三角形（通常使用等边三角形），沿三边中点的连线，将它分成四个小三角形，然后去掉中间的那一个小三角形。

接下来对其余三个小三角形重复上述操作，如图所示。

问题三：其他分形曲线或图形。

分形曲线还有很多，教材介绍了科赫曲线，其他还有皮亚诺曲线、分形树、康托（G. Cantor）三分集、Julia集、曼德布罗集合（Mandelbrot set），等等。