局部冲刷计算

参考资料
《城市防洪工程设计规范》（CJJ50-92）《防洪标准》（GB50201-94）
《堤防工程设计规范》（GB50286-98）1、护岸冲刷深度计算
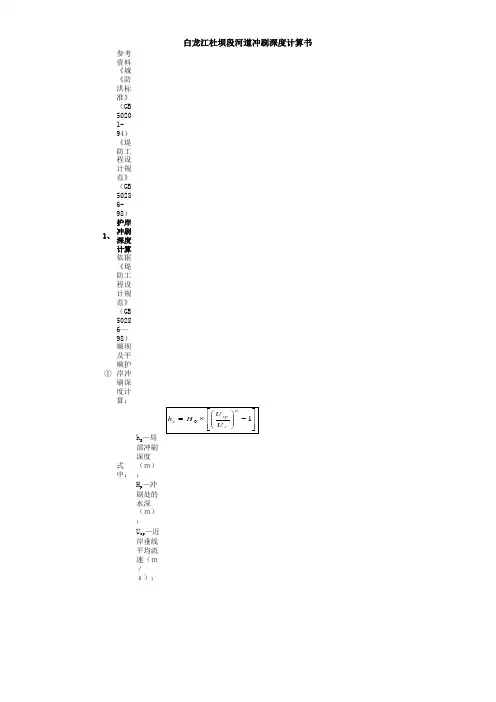
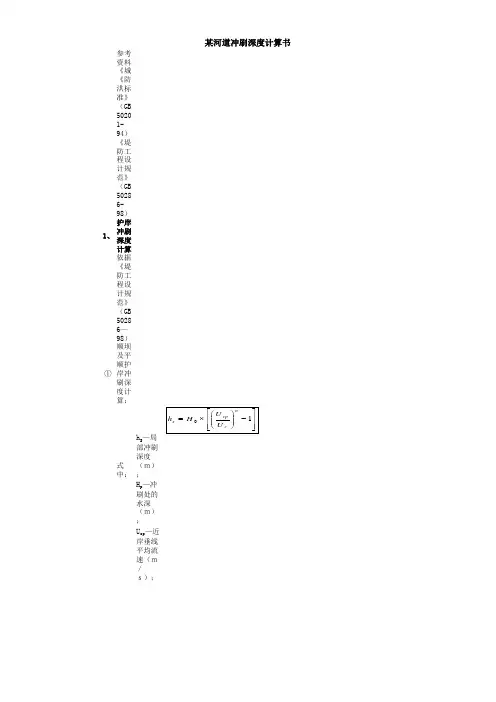
依据《堤防工程设计规范》（GB50286—98）①顺坝及平顺护岸冲刷深度计算：
式中：h S
H p —冲刷处的水深（ｍ）；
U cp —近岸垂线平均流速（ｍ／ｓ）；
U C —泥沙的启动流速（ｍ／ｓ）；粘性与沙质河床采用张瑞瑾公式计算，卵石
ｎ—与防护岸坡在平面上的形状有关，一般取ｎ＝1/4-1/6.河床采用长江科学院公式计算；
d
50—河床的中值粒径（ｍ）；H 0—行进水流水深（ｍ）；
r s ,r分别为泥沙与水的重度（KN/m 3),g为重力加速度（m/s 2).U cp 的计算应符合下列规定：
式中：
U—行近流速（ｍ／ｓ）；
η—水流流速分配不均匀系数，根据水流流向与岸坡交角α角查表采用。

② 结论:防洪堤基础冲刷深度平顺段及凸岸段设计值取1.5m,凹岸斜冲段设计值取2m.
白龙江杜坝段河道冲刷深度计算书。

4.4.1自然冲刷河床演变是一个非常复杂的自然过程，目前尚无可靠的定量分析计算方法，根据《公路工程水文勘测设计规范》（JTG C30—2002）中7.2条的要求，河床的自然冲刷是河床逐年自然下切的深度。

经深入调查，桥位处河段整体无明显自然下切现象，由于泥沙淤积，河床会逐年抬高，本次计算不考虑自然冲刷的情况。

4.4.2一般冲刷大桥建成后，由于受桥墩阻水影响，桥位断面过水断面减小，从而引起断面流速增大，水流挟沙能力也随之增大，会造成桥位断面河床冲刷。

根据地质勘察报告，桥位处河床为砂卵石层，河床泥沙平均粒径为40（mm ）。

按《公路工程水文勘测设计规范》（JTG C30—2002）的技术要求，非粘性土河床的一般冲刷可采用64—2简化公式计算：()max 66.029.02104.1h B B Q Q A h cc p ⎭⎬⎫⎩⎨⎧-⎪⎪⎭⎫ ⎝⎛=μλ公式中： h p ——桥下河槽一般冲刷后最大水深（m ）； Q 2——桥下河槽部分通过的设计流量（m 3/s ）； Q c ——天然状态下河槽流量（m 3/s ）；A ——单宽流量集中系数 15.0⎪⎪⎭⎫⎝⎛=H B A ；B C ——计算断面天然河床宽度（m ）；λ——设计水位下，桥墩阻水面积与桥下过水面积比值；μ——桥台前缘和桥墩两侧的漩涡区宽度与桥孔长度之比； B 2——桥下断面河床宽度（m ）； h max ——桥下河槽最大水深（m ）。

经计算：桥址处各设计频率一般冲刷深度成果见表4.4—1。

表4.4—1 XX 大桥一般冲刷计算成果表4.4.3局部冲刷根据XX 大桥桥型布置图，按《公路工程水文勘测设计规范》（JTG C30—2002）的技术要求，局部冲刷计算采用65—1修正式中的公式进行计算：当V ＞V 0时，10,00,'006.011,b )(K n V V V V v B K h v ⎭⎬⎫⎩⎨⎧---=ηξ h b —桥墩局部冲刷深度（m ）从一般冲刷后床面算起； K ξ—墩形系数，K ξ=1.05； K η1—河床颗粒影响系数； B 1—桥墩计算宽度；V—一般冲刷后墩前行近流速（m/s）；V0—河床泥沙起动流速（m/s）；V,0—墩前泥沙起冲流速（m/s）；n1—指数。

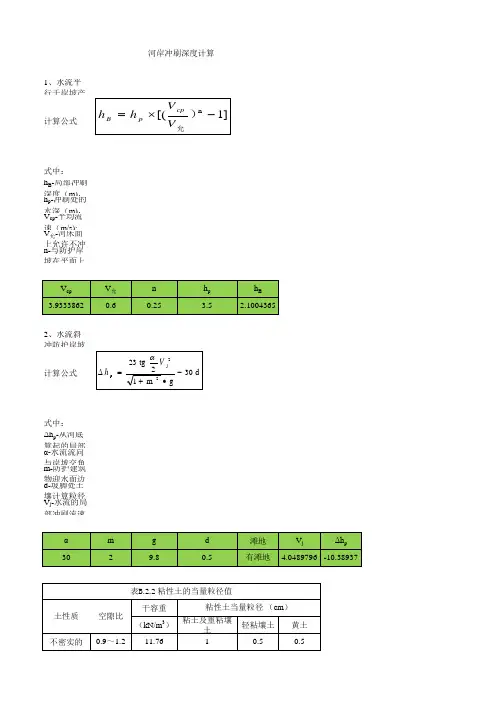
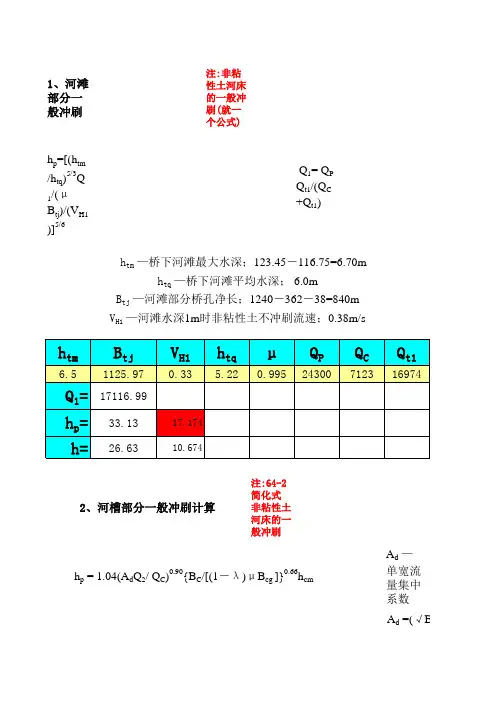
1、河滩部分一般冲刷注:非粘性土河床的一般冲刷(就一个公式)h p=[(h tm/h tq)5/3Q1/(μB tj)/(V H1)]5/6 Q1= Q P Q t1/(Q C +Q t1)h tm—桥下河滩最大水深；123.45－116.75=6.70mh tq—桥下河滩平均水深； 6.0mB tj—河滩部分桥孔净长；1240－362－38=840mV H1—河滩水深1m时非粘性土不冲刷流速；0.38m/s2、河槽部分一般冲刷计算注:64-2简化式 非粘性土河床的一般冲刷h p = 1.04(A d Q2/ Q C)0.90{B C/[(1－λ)μB cg ]}0.66h cm A d—单宽流量集中系A =(√B C/H C)0.15B C—天然状态下河槽宽度；362mH C—平滩水位时河槽平均水深；4.04mQ2—桥下河槽部分通过的设计流量；Q2= Q P Q C/(Q C +Q t1)3、河滩局部冲刷注:65-1按65-1式计算V=Ed1/6 h p2/3式中：V— 一般冲刷后墩前行进流速；V0=0.0246(h p/d)0.14√(332d+(10+ h p)/d0.72)E-含砂率，见P28式中：V0—河床泥沙起动流速；0.081748∵V > V0∴h b=KξKη1B10.6(V－V0’)/ [(V－V0’)/(V0－V0’)]n1式中：Kξ — 墩形系数； Kξ=1.10B1 — 桥墩计算宽度； B1=L－b=6－4=2mKη1 — 河床颗粒影响系数；Kη1 =0.8(1/d0.45+1/d0.15)V0’ — 墩前泥沙始冲流速；V0’=0.462(d/B1)0.06V0式中：d —河床泥沙平均粒径; 0.5mm (由地质资料可知)n1 —指数n1= (V0/V)**（0.25d-0.19）4、河槽桥墩局部冲刷按65—2式计算V0=0.28(d+0.7)0.5式中：V0—河床泥沙起动流速；V=(A d0.1/1.04)(Q2/ Q C)0.1{B C/[(1－λ)μB cg)]}0.34(h cm/h c)2/3V C式中：V— 一般冲刷后墩前行进流速；H C—平滩水位时河槽平均水深；4.04mQ2—桥下河槽部分通过的设计流量；Q2= Q P Q C/(Q C +Q t1)Q C—天然状态下河槽流量；6700 m3/sQ p —设计流量；13960 m3/s式中：V— 一般冲刷后墩前行进流速；V0’ — 墩前泥∵V > V0V0’=0.12(∴h b=KξKη2B10.6 h p0.15 [ (V－V0’)/V0]n2n2 —指式中：Kξ — 墩形系数； Kξ=1.10n2= (V0/V B1 — 桥墩计算宽度； B1=L－b=6－4=2mh p = 1.04(A d Q2/ Q C)0.90{B C/[(1－λ)μB cg)]}0.66h cmKη2 — 河床颗粒影响系数； Kη2 =0.375d0.24+0.0023/d2.2按6.2.1—1式计算,L j=K q(Q P/Q C)n3B c按6.2.1—2式计算, Lj=Q P/(βq C),β=1.19(Q c/Q t)0.10β—水流压缩系数q c —河槽平均单宽流量,q c=Q c/B c需要填充的数据床的一般冲刷—单宽流量集中系数d=(√B/H)0.15dA d—单宽流量集中系数A =(√B/H)0.15V0’ — 墩前泥沙始冲流速；V0’=0.12(d+0.5)0.55n2 —指数；n2= (V0/V)0.23+0.19lgd。

4.4.1自然冲刷河床演变是一个非常复杂的自然过程，目前尚无可靠的定量分析计算方法，根据《公路工程水文勘测设计规范》（JTG C30—2002）中7.2条的要求，河床的自然冲刷是河床逐年自然下切的深度。

经深入调查，桥位处河段整体无明显自然下切现象，由于泥沙淤积，河床会逐年抬高，本次计算不考虑自然冲刷的情况。

4.4.2一般冲刷大桥建成后，由于受桥墩阻水影响，桥位断面过水断面减小，从而引起断面流速增大，水流挟沙能力也随之增大，会造成桥位断面河床冲刷。

根据地质勘察报告，桥位处河床为砂卵石层，河床泥沙平均粒径为40（mm ）。

按《公路工程水文勘测设计规范》（JTG C30—2002）的技术要求，非粘性土河床的一般冲刷可采用64—2简化公式计算：()max 66.029.02104.1h B B Q Q A h cc p ⎭⎬⎫⎩⎨⎧-⎪⎪⎭⎫ ⎝⎛=μλ公式中： h p ——桥下河槽一般冲刷后最大水深（m ）； Q 2——桥下河槽部分通过的设计流量（m 3/s ）； Q c ——天然状态下河槽流量（m 3/s ）；A ——单宽流量集中系数 15.0⎪⎪⎭⎫⎝⎛=H B A ；B C ——计算断面天然河床宽度（m ）；λ——设计水位下，桥墩阻水面积与桥下过水面积比值；μ——桥台前缘和桥墩两侧的漩涡区宽度与桥孔长度之比； B 2——桥下断面河床宽度（m ）； h max ——桥下河槽最大水深（m ）。

经计算：桥址处各设计频率一般冲刷深度成果见表4.4—1。

表4.4—1 XX 大桥一般冲刷计算成果表4.4.3局部冲刷根据XX 大桥桥型布置图，按《公路工程水文勘测设计规范》（JTG C30—2002）的技术要求，局部冲刷计算采用65—1修正式中的公式进行计算：当V ＞V 0时，10,00,'006.011,b )(K n V V V V v B K h v ⎭⎬⎫⎩⎨⎧---=ηξ h b —桥墩局部冲刷深度（m ）从一般冲刷后床面算起； K ξ—墩形系数，K ξ=1.05； K η1—河床颗粒影响系数； B 1—桥墩计算宽度；V —一般冲刷后墩前行近流速（m/s ）；V0—河床泥沙起动流速（m/s）；V,0—墩前泥沙起冲流速（m/s）；n1—指数。

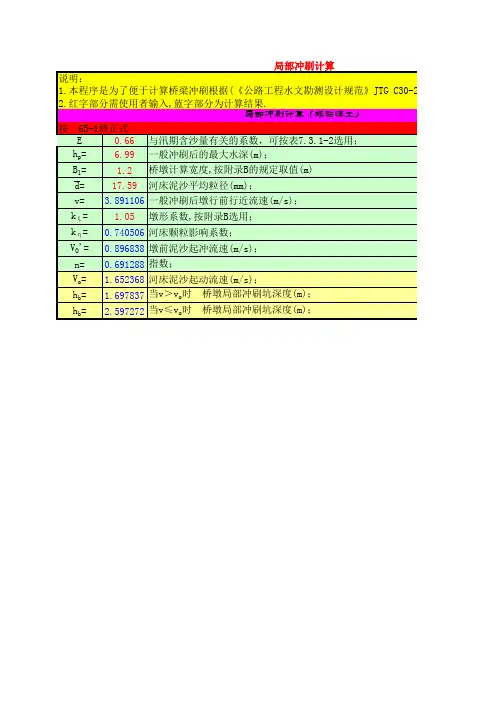
一般冲刷计算公式：cm cg cc d p h B B Q Q A h 66.090.02)1(04.1⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛=μλ12t c cQ Q Q Q +=15.0⎪⎪⎭⎫⎝⎛=z z d H B A式中：h p ——桥下一般冲刷后的最大水深(m)； Q p ——频率为P ％的设计流量(m 3/s)；Q 2——桥下河槽部分通过的设计流量(m 3/s)，当河槽能扩宽至全桥时取用Q p ； Q c ——天然状态下河槽部分设计流量(m 3/s)； Q t1——天然状态下桥下河滩部分设计流量(m 3/s)；B cg ——桥长范围内的河槽宽度(m)，当河槽能扩宽至全桥时取用桥孔总长度； B z ——造床流量下的河槽宽度(m)，对复式河床可取平滩水位时河槽宽度； λ——设计水位下，在B cg 宽度范围内，桥墩阻水总面积与过水面积的比值； μ——桥墩水流侧向压缩系数； h cm ——河槽最大水深(m)；A d ——单宽流量集中系数，山前变迁、游荡、宽滩河段当A d >1.8时，A d 值可采用1. 8；H z ——造床流量下的河槽平均水深(m)，对复式河床可取平滩水位时河槽平均水深。

②非粘性土河床桥墩局部冲刷计算桥渡冲刷的产生是由于桥墩阻碍了水流，使水流形态发生变化，一般在墩前两侧发生集中现象，引起动能增加；另一方面水流受阻后部分动能转化为位能，由于水流形态变化，桥墩附近水流冲刷能力加大，在桥墩处产生冲刷坑。

局部冲刷计算公式当V ≤V 0时，⎪⎪⎭⎫ ⎝⎛-=0015.06.012'V V V h B K K h pb ηε当V ＞V 0时，20015.06.012'n pb V V V h B K K h ⎪⎪⎭⎫ ⎝⎛-=ηε24.02.22375.00023.0d dK +=η5.00)7.0(28.0+=d V 55.00)5.0(12.0'+=d Vd V Vn lg 19.023.002)(+=式中：h b ——桥墩局部冲刷深度(m)： K ξ——墩形系数； B1——桥墩计算宽度(m)； h p ——一般冲刷后的最大水深(m)； d ——河床泥沙平均粒径(mm)； K η2——河床颗粒影响系数；V ——一般冲刷后墩前行近流速(m/s)， V o ——河床泥沙起动流速(m/s)； V ,0——墩前泥沙起冲流速(m/s)； n 2 ——指数。

２０２０年第３期２０２０Ｎｕｍｂｅｒ３水电与新能源ＨＹＤＲＯＰＯＷＥＲＡＮＤＮＥＷＥＮＥＲＧＹ第３４卷Ｖｏｌ.３４ＤＯＩ:１０.１３６２２/ｊ.ｃｎｋｉ.ｃｎ４２－１８００/ｔｖ.１６７１－３３５４.２０２０.０３.００９收稿日期:２０１９－１１－０４作者简介:张晓蕊ꎬ女ꎬ助理工程师ꎬ主要从事风电基础结构设计及相关工作ꎮ海上风机单桩基础局部冲刷计算分析张晓蕊ꎬ吴子昂ꎬ戴东鹰(上海勘测设计研究院ꎬ上海㊀２００３３５)摘要:依据波㊁流联合作用下的韩海骞公式计算江苏某海上风电场桩基局部冲刷深度ꎬ再采用ＳＡＣＳ软件对结构进行分析结果表明ꎬ局部冲刷增加桩身侧向位移ꎬ降低整机频率ꎬ疲劳损伤大ꎮ解决这些问题可通过加大桩径和桩长ꎬ要设计出既经济又安全的基础尺寸ꎬ还需结合实际工程的冲刷观测结果进行更准确的预测ꎮ关键词:单桩ꎻ局部冲刷ꎻ频率ꎻ疲劳损伤中图分类号:ＴＫ８３㊀㊀㊀文献标志码:Ａ㊀㊀㊀文章编号:１６７１－３３５４(２０２０)０３－００３３－０５ＣａｌｃｕｌａｔｉｏｎａｎｄＡｎａｌｙｓｉｓｏｆＬｏｃａｌＳｃｏｕｒｏｆＭｏｎｏｐｉｌｅＦｏｕｎｄａｔｉｏｎｏｆＯｆｆｓｈｏｒｅＷｉｎｄＴｕｒｂｉｎｅｓＺＨＡＮＧＸｉａｏｒｕｉꎬＷＵＺｉ ａｎｇꎬＤＡＩＤｏｎｇｙｉｎｇ(ＳｈａｎｇｈａｉＩｎｖｅｓｔｉｇａｔｉｏｎꎬＤｅｓｉｇｎ＆ＲｅｓｅａｒｃｈＩｎｓｔｉｔｕｔｅＣｏ.ꎬＬｔｄ.ꎬＳｈａｎｇｈａｉ２００３３５ꎬＣｈｉｎａ)Ａｂｓｔｒａｃｔ:ＴｈｅｌｏｃａｌｓｃｏｕｒｄｅｐｔｈｏｆｔｈｅｗｉｎｄｔｕｒｂｉｎｅｓｉｎａｎｏｆｆｓｈｏｒｅｗｉｎｄｆａｒｍｉｎＪｉａｎｇｓｕＰｒｏｖｉｎｃｅｉｓｃａｌｃｕｌａｔｅｄｕｓｉｎｇｔｈｅＨａｎＨａｉｑｉａｎｆｏｒｍｕｌａｕｎｄｅｒｔｈｅｃｏｍｂｉｎｅｄａｃｔｉｏｎｏｆｗａｖｅａｎｄｃｕｒｒｅｎｔ.ＴｈｅｎꎬｔｈｅｐｉｌｅｓｔｒｕｃｔｕｒｅｉｓａｎａｌｙｚｅｄｕｓｉｎｇＳＡＣＳｓｏｆｔｗａｒｅ.Ｔｈｅｒｅｓｕｌｔｓｓｈｏｗｔｈａｔｌｏｃａｌｓｃｏｕｒｍａｙｉｎｃｒｅａｓｅｔｈｅｌａｔｅｒａｌｄｉｓｐｌａｃｅｍｅｎｔｏｆｔｈｅｐｉｌｅꎬｒｅｄｕｃｅｔｈｅｆｒｅｑｕｅｎｃｙｏｆｔｈｅｗｈｏｌｅｕｎｉｔꎬａｎｄａｇｇｒａｖａｔｅｔｈｅｆａｔｉｇｕｅｄａｍａｇｅ.Ｔｈｅｓｅｐｒｏｂｌｅｍｓｃａｎｂｅｓｏｌｖｅｄｂｙｉｎｃｒｅａｓｉｎｇｔｈｅｐｉｌｅｄｉａｍｅｔｅｒａｎｄｐｉｌｅｌｅｎｇｔｈ.Ｈｏｗｅｖｅｒꎬｉｔｉｓｎｅｃｅｓｓａｒｙｔｏｍａｋｅｍｏｒｅａｃｃｕｒａｔｅｌｏｃａｌｓｃｏｕｒｐｒｅｄｉｃｔｉｏｎｂａｓｅｄｏｎａｃｔｕａｌｏｂｓｅｒｖａｔｉｏｎｒｅｓｕｌｔｓｔｏｇｅｔｅｃｏｎｏｍｉｃａｎｄｓａｆｅｆｏｕｎｄａｔｉｏｎｄｉｍｅｎｓｉｏｎｓ.Ｋｅｙｗｏｒｄｓ:ｍｏｎｏｐｉｌｅꎻｌｏｃａｌｓｃｏｕｒꎻｆｒｅｑｕｅｎｃｙꎻｆａｔｉｇｕｅｄａｍａｇｅ㊀㊀海上风电作为一种可再生清洁能源ꎬ已经得到了全世界广泛的关注ꎮ海上风资源丰富ꎬ同时环境也更加复杂ꎮ需要注意的是ꎬ桩基础泥面位置由于波浪和海流的作用ꎬ会产生局部冲刷从而导致风机整体的稳定性降低ꎮ因此ꎬ针对海上风机基础局部冲刷问题开展一系列分析ꎬ将具有十分重要的工程意义[１－２]ꎮ目前ꎬ海上风电场风机基础局部冲刷深度主要依靠经验公式或根据已有的工程场区资料做参考ꎮ但由于场区资料较少ꎬ且各个海域环境相差甚远ꎬ经验公式一般作为首选方法ꎮ本文针对江苏某风电场ꎬ对比不同冲刷深度下结构频率㊁变形㊁承载力和疲劳寿命等的变化ꎬ分析特定海洋环境下局部冲刷对风力机基础结构的影响ꎮ１㊀经验公式及验证目前国内外用于局部冲刷深度计算的经验公式主要有以下三种ꎬ韩海骞公式ꎬ王汝凯公式和Ｊ＆Ｓ公式[３]ꎮ１.１㊀经验公式１)韩海骞公式ꎮ浙江大学的韩海骞建立了单一潮流作用下桥墩局部冲刷计算公式ꎮｈｂｈ＝１７.４ｋ１ｋ２(Ｂｈ)０.３２６(ｄ５０ｈ)０.１６７Ｆｒ０.６２８(１)式中:ｈｂ为潮流作用下桥墩最大局部冲刷深度ꎬｍꎻｈ为全潮最大水深ꎬｍꎻＢ为最大水深下平均阻水宽度ꎬｍꎻｄ５０为河床泥沙的中值粒径ꎬｍꎻＦｒ为弗劳德数ꎻｇ为重力加速度ꎻｋ１为基础平面布置系数ꎬ条形取１.０ꎬ３３水电与新能源２０２０年第３期梅花形取０.８６２ꎻｋ２为基础垂直布置系数ꎬ直桩取１.０ꎬ斜桩取１.１７６ꎮ韩海骞公式适用范围:平均阻水宽度Ｂ为０.８~４２.０ｍꎻ全潮最大流速ｕ为１.４~８.０ｍ/ｓꎻ全潮最大水深ｈ为４.５~３１.０ｍꎻ中值粒径ｄ５０为０.００８~０.１４ｍｍꎮ(２)王汝凯公式ꎮ王汝凯和Ｈｅｒｂｉｃｈ基于粗砂模型ꎬ进行了波㊁流共同作用下小直径桩的局部冲刷研究ꎬ并建立了局部冲刷深度计算公式ꎮｌｇＳｕ１ｈ＝－１.２９３５＋０.１９１７ｌｇβ(２)β＝ＮｆＨＬＵｒＮｓＮｒｐ＝Ｈ２ＬＶ３Ｄ[Ｖ＋(１/Ｔ－Ｖ/Ｌ)ＨＬ/２ｈ]２[(ρｓ－ρ)/ρ]υｇ２ｈ４ｄ５０(３)式中:Ｎｆ为水流弗劳德数的平方ꎻＶ为行近流速ꎬｍ/ｓꎻｇ为重力加速度ꎬｍ/ｓ２ꎻｈ为行近水深ꎬｍꎻＨ为波高ꎬｍꎻＬ为波长ꎬｍꎻＴ为周期ꎬｓꎻＵｒ为Ｕｒｓｅｌｌ数ꎻＮｓ为颗粒ｓｅｄｉｍｅｎｔ数ꎬＮｓ＝Ｖｆｗ２/[(ρｓ－ρ)/ρ]ｇｄ５０ꎻＶｆｗ为波流合成速度ꎬｍ/ｓꎻρｓ为泥沙密度ꎬｋｇ/ｍ３ꎻρ为水密度ꎬｋｇ/ｍ３ꎻｄ５０位泥沙的中值粒径ꎬｍｍꎻＮｒｐ为桩的雷诺数ꎻＤ为桩径ꎬｍꎻυ为运动粘滞系数ꎬｍ２/ｓꎮ３)Ｊ＆Ｓ公式ꎮＪｏｎｅｓ和Ｓｈｅｐｐａｒｄ提出了仅考虑流速的大型桥墩局部冲刷计算公式ꎮＤｓｄｐ＝ｃ２(Ｖｕｓｐｂ－ＶＶｃｒ)＋ｃ３(４)ｃ２＝(ｋ－ｃ３)(ＶｕｓｐｂＶｃｒ－１)－１(５)ｃ３＝２.４ｔａｎｈ[２.１８(Ｄｄｐ)２/３](６)ｋ＝ｔａｎｈ[２.１８(Ｄｄｐ)２/３][－０.２７９＋０.０４９ｅｘｐ(ｌｇｄｐｄ５０)＋０.７８(ｌｇｄｐｄ５０)－１]－１(７)式中:Ｄｓ为桩基极限冲刷深度ꎬｍꎻｄｐ为桩径ꎬｍꎻＤ为水深ꎬｍꎻＶ为底部最大平均流速ꎬｍ/ｓꎻＶｃｒ为泥沙临界起动速度ꎬｍ/ｓꎻＶｕｓｐｂ为垂线平均流速ꎬｍ/ｓꎻｄ５０为泥沙中值粒径ꎬｍꎮ１.２㊀公式验证根据已有的埕岛油田海域环境条件(见表１)及冲刷数据[４]ꎬ对上述经验公式进行适用性验证ꎮ由于韩海骞公式和Ｊ＆Ｓ公式仅考虑流速的影响ꎬ现参考«港口与航道水文规范»得到波浪水质点的平均流速与潮流速度之和带入公式进行计算ꎬ结果见表２ꎮ表１㊀埕岛油田环境参数表平台水深/ｍ波速/(ｍ ｓ－１)波高/ｍ波周期/ｓ桩径/ｍ中值粒径/ｍｍＣＢ２５Ｃ９.６００.９０４.５０８.６０１.２００.０５ＣＢ１２Ｃ１２.６００.９０４.５０８.６０１.２００.０５表２㊀平台局部冲刷深度及实测值表ｍ㊀平台韩海骞公式王汝凯公式Ｊ＆Ｓ公式实测ＣＢ２５Ｃ３.７７４.４２２.７４３.０~３.５ＣＢ１２Ｃ３.７９４.６７２.６９㊀㊀从表２可以看出:适用粗砂的王汝凯公式在淤泥质土或细砂条件下ꎬ冲刷深度被放大ꎬ其计算结果比实测值大４０％左右ꎬ过于保守ꎬ在实际工程中经济性较低ꎻＪ＆Ｓ公式虽然考虑了波流联合作用ꎬ但结果仍偏低ꎬ不推荐采用ꎻ考虑波流联合作用的韩海骞公式计算结果与实测值较为接近ꎬ实测值为经验公式的８０％~９０％ꎮ本文环境条件为近海海域ꎬ波浪对海底的影响不能忽视ꎬ所以采用考虑波流作用下的韩海骞公式进行局部冲刷计算ꎮ２㊀ＳＡＣＳ计算原理ＳＡＣＳ(ＳｔｒｕｃｔｕｒａｌＡｎａｌｙｓｉｓＣｏｍｐｕｔｅｒＳｙｓｔｅｍ)是基于有限元分析的结构仿真平台ꎬ能够进行复杂海洋环境下的结构静力和动力性能分析ꎮ静力分析模块主要包括线弹性静力分析㊁桩－土－结构相互作用的非线性静力分析等ꎮ动力分析模块主要包括模态分析㊁疲劳分析ꎬ以及波浪作用分析等[５]ꎮ本文后续内容将采用ＳＡＣＳ软件对风机基础结构性能进行计算分析ꎮ３㊀风机基础局部冲刷计算３.１㊀环境条件本文针对江苏某海上风场进行单桩基础局部冲刷计算分析ꎬ具体环境条件如表３所示ꎮ采用波流联合作用下的韩海骞公式ꎬ分析桩径㊁中值粒径对冲刷深度的影响程度ꎮ表３㊀江苏某海域环境条件表机位水深(设计高水位)/ｍ流速/(ｍ ｓ－１)波高/ｍ波周期/ｓ波长/ｍ中值粒径/ｍｍＦ３０１１.０４１.１５３.９９７.３６６６０.０７０９Ｆ４７８.０７１.１５３.９９７.３６５９０.０１５３４３张晓蕊ꎬ等:海上风机单桩基础局部冲刷计算分析２０２０年３月㊀㊀根据表３中的数据ꎬ变换基础结构形式和尺寸ꎬ计算Ｆ３０㊁Ｆ４７机位特定地质条件下的局部冲刷深度ꎬ得到图１(ａ)ꎮ从图１(ａ)中可以看出ꎬＦ３０㊁Ｆ４７机位４ｍ直径斜桩和将近７ｍ直径的直桩冲刷深度接近ꎻ１ｍ直径斜桩和将近２ｍ直径的直桩冲刷深度接近ꎬ从公式中也可计算得出相同冲刷深度的斜桩直径是直桩的０.６０８倍ꎮ小直径桩的多脚架基础和高桩承台对局部冲刷不如单桩敏感ꎬ但在实际工程中ꎬ单桩基础由于结构相对简单ꎬ海上施工作业期短ꎬ施工可靠性高等优点ꎬ成为颇受欢迎的一种基础型式ꎮ为防止钢管桩桩周冲刷ꎬ沿基础一定范围内会进行防冲刷地基处理ꎮ本文风场最大水深８~１１ｍꎬ变化范围不大ꎮ从图１(ｂ)中可以看出ꎬ水深对冲刷深度的影响较小ꎬ仅１.３％ꎮ图(ａ)㊁(ｂ)中的曲线均随着ｘ轴变量的增大而增大ꎬ而曲线斜率随ｘ变量的增大而减小ꎮ图１㊀局部冲刷结果图３.２㊀计算分析风机基础局部冲刷深度大多根据经验公式估算ꎬ在结构设计时放出相应的裕度ꎮ但经验公式适用条件为单向流ꎬ本场区实际为旋转流ꎬ流向并不固定ꎬ经验公式结果将放大波流对冲刷的影响ꎮ本文将对经验公式的局部冲刷深度计算结果进行适当折减ꎬ再通过ＳＡＣＳ软件进行相应的结构受力变形等分析ꎮＦ３０㊁Ｆ４７机位拟采用３.３ＭＷ风机ꎬ塔筒底部直径为５.５ｍꎬ单桩基础顶高程１１ｍꎬ整机允许频率范围０.２５８~０.２７６ＨｚꎮＦ４７机位结构直径５.５ｍꎬ采用波㊁流联合作用下的韩海骞公式得到冲刷深度为５.２８ｍꎬ对比不同折减系数下的结构静力计算结果ꎬ如表４所示ꎮ表４㊀Ｆ４７结构(Ｄ＝５.５ｍ)计算结果表冲刷深度/ｍ频率/Ｈｚ泥面转角/ɢ桩尖位移/ｃｍ桩身最大ＵＣ抗压承载力/ｋＮ桩身最大压力/ｋＮ００.２６１６３.８７２９０.０４４０.４２３－２９４３１.０－１１６２６.３４.２２(折减系数０.８)０.２５８１３.８０８８０.１０２０.４５０－２８９４７.１－１１６２２.８４.７５(折减系数０.９)０.２５７６３.７９７７０.１１１０.４５３－２８８１４.７－１１６１２.０５.２８０.２５７１３.７８２６０.１２３０.４５５－２８６９３.１－１１６０４.２注:承载力考虑安全系数１.５ꎻ结构压力乘以１.１倍放大系数ꎮ㊀㊀由表４可以看出ꎬ同样的结构在不考虑冲刷时满足变形频率等要求ꎬ但是在折减系数为０.８时整机频率就十分接近安全范围的下界了ꎬ完全不考虑折减则更加无法满足频率要求ꎬ此时的变形和受力结果依然满足规范ꎬ结构尺寸以频率控制为主ꎮ选取适当的结构尺寸ꎬ需要与冲刷深度进行进一步的迭代计算ꎮ为提高频率的安全裕度重新建立直径５.５~５.７ｍ的单桩模型ꎬ考虑到海流为旋转流ꎬ我们取折减系数０.８的冲刷深度ꎬ得到冲刷深度为４.２７ｍꎬ具体计算结果如表５ꎬ桩身位移曲线收敛如图２ꎮ５３水电与新能源２０２０年第３期表５㊀Ｆ４７结构(Ｄ＝５.５~５.７ｍ)计算结果表冲刷深度/ｍ频率/Ｈｚ泥面转角/ɢ桩尖位移/ｃｍ桩身最大ＵＣ抗压承载力/ｋＮ桩身最大压力/ｋＮ４.２７０.２６１７３.５０６００.１２１０.４２３－２９８０４.９－１１７９９.５注:承载力考虑安全系数１.５ꎻ结构压力乘以１.１倍放大系数ꎮ图２㊀Ｆ４７(Ｄ＝５.５~５.７ｍ)桩身位移曲线图㊀㊀Ｆ３０机位表层土为厚度１.３ｍ的砂质粉土(ｄ５０＝０.０７０９)ꎬ第二层是厚度１０.７ｍ的淤泥质粘土(ｄ５０＝０.０１５３ｍｍ)ꎬ由于表层土较薄ꎬ计算局部冲刷时中值粒径选取０.０１５３ｍｍ(见表６)ꎮ由表６和图３可以看出ꎬＦ３０基础桩径比Ｆ４７增大了０.２ｍꎬ使得泥面转角减小ꎬ但由于浅层土壤较表６㊀Ｆ３０结构(Ｄ＝５.５~５.９ｍ)计算结果表冲刷深度/ｍ频率/Ｈｚ泥面转角/ɢ桩尖位移/ｃｍ桩身最大ＵＣ抗压承载力/ｋＮ桩身最大压力/ｋＮ００.２６１１３.５１７７０.１５３０.３７２－３０９３６.６－１２８５９.７４.３７(折减系数０.８)０.２５７５３.４６９９０.２７５０.３９４－３０３９２.９－１２８５５.７４.９２(折减系数０.９)０.２５７０３.４６４２０.２９６０.３９６－３０３１８.７－１２８５５.１５.４７０.２５６６３.４６１１０.３１７０.３９８－３０２５７.０－１２８５４.７注:承载力考虑安全系数１.５ꎻ结构压力乘以１.１倍放大系数ꎮ差ꎬ整机频率仍然难以满足规定要求ꎬ且桩径的增大也加大了波浪力的作用ꎬ使得桩身位移曲线不收敛ꎮ解决这一系列问题ꎬ需增加桩径和桩长ꎮ重新建立直径５.５~６.１ｍ的单桩模型ꎬ桩长增加４ｍꎬ考虑到海流为旋转流ꎬ我们取折减系数０.８的冲刷深度ꎬ得到冲刷深度为４.４２ｍꎬ具体计算结果如表７ꎬ桩身位移曲线收敛如图４ꎮ图３㊀Ｆ３０(Ｄ＝５.５~５.９ｍꎬ冲刷４.３７ｍ)桩身位移曲线图表７㊀Ｆ３０结构(Ｄ＝５.５~６.１ｍ)计算结果表冲刷深度/ｍ频率/Ｈｚ泥面转角/ɢ桩尖位移/ｃｍ桩身最大ＵＣ抗压承载力/ｋＮ桩身最大压力/ｋＮ４.４２０.２６０５０.００３１５７３０.１１９０.３６６－３１９６９.５－１３０４０.０注:承载力考虑安全系数１.５ꎻ结构压力乘以１.１倍放大系数ꎮ㊀㊀综上可得ꎬＦ４７机位若要满足折减系数０.８的局部冲刷深度要求ꎬ结构最大桩径要在５.５ｍ基础上增加０.２ｍꎬ钢管桩重量增加将近１７ｔꎻＦ３０机位若要满足折减系数０.８的局部冲刷深度要求ꎬ结构最大桩径要在５.９ｍ基础上增加０.２ｍꎬ且桩长增加４ｍꎬ钢管桩重量增加将近５３ｔꎮ冲刷主要影响的是实际入泥深度ꎬ所以对整机频率和桩身侧向位移会有一定影响ꎮ单桩基础的刚度较小ꎬ表层土的冲刷对基础变位极其不利ꎬ所以通常会对海床表层土进行防冲刷处理ꎬ例如投放沙袋ꎬ砂被ꎬ连锁排和固化土等措施ꎮ如何既经济又安全的设计出最理想的基础方案ꎬ需要不断尝试并结合实际工程的观测结果进行更准确的预测ꎮ６３张晓蕊ꎬ等:海上风机单桩基础局部冲刷计算分析２０２０年３月图４㊀Ｆ３０(Ｄ＝５.５~６.１ｍ)桩身位移曲线图３.３㊀疲劳分析选取Ｆ４７机位进行疲劳分析ꎬ由于缺乏一体化的载荷输入ꎬ本文将保守地采用风载荷损伤与波浪谱疲劳损伤直接相加的方式得到最终损伤值ꎮ设计疲劳安全系数为２ꎬ寿命２５年ꎮ对比不同桩径ꎬ不同冲刷深度对结构疲劳寿命的影响ꎬ原泥面高程－５.４９ｍꎬ钢管桩３ｍ一段ꎬ具体计算结果见表８ꎮ从表８可以看出ꎬＦ４７基础Ｄ＝５.５ｍ时冲刷４.２２ｍ最大疲劳损伤是不冲刷的１.７倍ꎻＤ＝５.５~５.７ｍ时冲刷４.２７ｍ最大疲劳损伤是冲刷４.２２ｍ的１.０１倍ꎮ相同结构在考虑冲刷时整机频率相对降低ꎬ结构更柔ꎬ所以疲劳损伤更大ꎮＤ＝５.５~５.７ｍ结构变径段高程２~－１ｍꎬ－１ｍ到桩尖位置桩径５.７ｍꎮ风机载荷和波浪载荷当结构尺寸增大时ꎬ产生的疲劳损伤减小ꎬ但初始变径位置波浪损伤稍稍增大ꎮ综上ꎬ针对Ｆ４７机位选取Ｄ＝５.５~５.７ｍ结构尺寸ꎬ满足疲劳计算要求ꎮ表８㊀Ｆ４７基础疲劳损伤计算结果表高程Ｄ＝５.５ｍꎬ冲刷０ｍ风机载荷损伤波浪载荷损伤总损伤Ｄ＝５.５ｍꎬ冲刷４.２２ｍ风机载荷损伤波浪载荷损伤总损伤Ｄ＝５.５~５.７ｍꎬ冲刷４.２２ｍ风机载荷损伤波浪载荷损伤总损伤Ｄ＝５.５~５.７ｍꎬ冲刷４.２７ｍ风机载荷损伤波浪载荷损伤总损伤１１０.０５００.００００.０５００.０５００.００００.０５００.０５００.００００.０５００.０５００.００００.０５０８０.０３４０.０５６０.０９００.０３４０.１１８０.１５２０.０３４０.１１８０.１５２０.０３４０.１２００.１５４５０.０３４０.０６００.０９４０.０３４０.１２７０.１６１０.０３４０.１２７０.１６１０.０３４０.１２９０.１６３２０.０２６０.０４９０.０７５０.０２６０.１０３０.１２９０.０２６０.１０４０.１３００.０２６０.１０５０.１３１－１０.０２１０.０４４０.０６５０.０２１０.０９５０.１１６０.０１５０.０６７０.０８２０.０１５０.０６７０.０８２－４０.０２１０.０４７０.０６８０.０２１０.１０２０.１２３０.０１５０.０７２０.０８７０.０１５０.０７３０.０８８－７０.０２１０.１１２０.１３３０.０１５０.０７９０.０９４０.０１５０.０８００.０９５４㊀结㊀语１)通过和现有工程实测冲刷深度进行对照ꎬ波㊁流联合作用下的韩海骞经验公式计算结果比王汝凯㊁Ｊ＆Ｓ公式更接近实际ꎬ且数值略大偏安全ꎮ２)局部冲刷主要影响的是实际入泥深度ꎬ所以对整机频率和桩身侧向位移会有一定影响ꎬ一般通过增加桩径和桩长来解决ꎮ如何既经济又安全的设计出最理想的基础方案ꎬ需要不断尝试并结合实际工程的观测结果进行更准确的预测ꎮ３)针对本风场的Ｆ４７机位基础ꎬ相同结构在冲刷深度大时整机频率相对降低ꎬ结构更柔ꎬ所以疲劳损伤更大ꎻ相同冲刷深度条件下ꎬ大尺寸桩径部位的疲劳损伤较小ꎬ但变径段的小直径部位的损伤值稍稍增大ꎮ参考文献:[１]祁一鸣ꎬ陆培东ꎬ曾成杰ꎬ等.海上风电桩基局部冲刷试验研究[Ｊ].水利水运工程学报ꎬ２０１５(６):６０－６７[２]刘超ꎬ孙文ꎬ张积乐ꎬ等.海上风电场单桩基础结构冲刷实验研究[Ｊ].太阳能学报ꎬ２０１６ꎬ３７(２):３１６－３２１[３]张玮ꎬ濮勋ꎬ廖迎娣.淤泥质海岸近海风电塔基局部冲刷计算研究[Ｊ].海洋工程ꎬ２０１０ꎬ２８(２):１０５－１０９[４]王卫远ꎬ杨娟ꎬ李睿元.海上风电场风机桩基局部冲刷计算[Ｊ].中国港湾建设ꎬ２０１１ꎬ３１(６):１３－１５[５]陈晶.导管架式海上风电基础结构分析[Ｄ].天津:天津大学ꎬ２０１４７３。