材料力学 第七章 弯曲应力
- 格式:ppt
- 大小:2.37 MB
- 文档页数:59



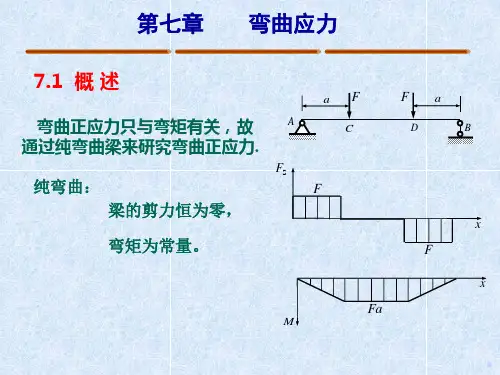
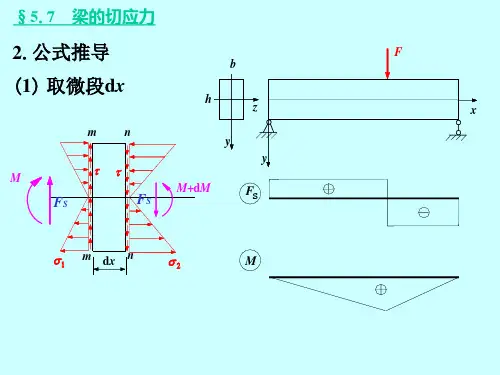






第七章弯曲应力一、教学目标和教学内容一、教学目标⑴把握梁纯弯曲时横截面上正应力计算公式的推导进程,明白得推导中所作的大体假设。
⑵明白得横力弯曲正应力计算仍用纯弯曲公式的条件和近似程度。
⑶把握中性层、中性轴和翘曲等大体概念和含义。
⑷把握各类形状截面梁(矩形、圆形、圆环形、工字形)横截面上切应力的散布和计算。
⑸熟练弯曲正应力和剪应力强度条件的成立和相应的计算。
⑹了解什么情形下需要对梁的弯曲切应力进行强度校核。
⑺从弯曲强度条件动身,把握提高弯曲强度的假设干方法。
⑻明白得等强度梁的概念。
⑼确信薄壁杆件切应力流的方向。
⑽明白得弯曲中心对开口薄壁杆件的重要性,把握确信弯曲中心的方式。
二、教学内容⑴梁纯弯曲和横力弯曲时横截面上的正应力⑵梁横力弯曲时横截面上的切应力⑶提高弯曲强度的假设干方法、薄壁杆件的切应力流和弯曲中心。
二、重点难点⑴重点:纯弯曲梁横截面上正应力公式的分析推导。
横力弯曲横截面上正应力的计算,最大拉应力和最大压应力的计算。
弯曲的强度计算。
弯曲横截面上的剪应力。
重点处置:从弯曲变形的特点动身,让学生了解两个应力的散布规律,并对两个应力的散布进行对照,增强学生明白得和经历。
分析弯曲正应力、剪应力公式中各项的意义,计算方式,结合T 型截面梁铸铁梁.这一典型问题分析,并在作业中进一步强化训练。
难点:弯曲正应力、剪应力推导进程和弯曲中心的概念。
难点处置: 结合梁弯曲变形的特点,推导两个应力公式,在推导中,充分利用前面的知识,发挥学生的主动性,让学生自己选择解决方式,增强学生对内容的把握。
对照A N=σ,pt I M =τ的推导消化难点,以学生明白得这一推导思路。
结合纯弯曲的条件和两个方向平面弯曲明白得弯曲中心。
三、教学方式采纳启发式教学,通过提问,引导学生试探,让学生回答下列问题。
四、建议学时 8学时 五、实施学时 六、讲课提纲一、几个大体概念 ⑴平面弯曲和弯曲中心变形后梁轴线的位移方向沿着加载方向的弯曲情形,称为平面弯曲。