正比例函数和反比例函数的区别(附图)

正比例函数与反比例函数
正比例函数是指当自变量（x）增大时，因变量（y）也随之增大，并且二者的变化满足一个常数比的关系。

可以表示为y=kx，其中k是常数，称为比例常数。

当x=0时，y=0。

反比例函数是指当自变量（x）增大时，因变量（y）则相应减小，并且二者的乘积满足一个常数的关系。

可以表示为y=k/x，其中k是常数，称为比例常数。

当x=0时，函数无定义，因为不能除以0。

正比例函数和反比例函数是数学中常见的基本函数，可以在许多实际问题中找到应用。

根据函数的性质和特点，我们可以用它们来描述和解决各种实际问题，如人口增长、速度与时间的关系等。

通过研究和应用正比例函数和反比例函数，我们可以更好地理解和分析各种现象和数据的变化规律。

y
Байду номын сангаас
3
.x
y
pN
M ox
2020年10月2日
21
例5:如右图点为反比例函数上一点,若图中
阴影部分即三角形AOB的面积为4,求反比
例函数的解析式
y
oA x
B
2020年10月2日
22
练一练 7
一个反比例函数的图象在第二象限，如图，点A是 图象上任意一点，AM⊥x轴于点M，O是原点，如 果△AOM的面积为3，求这个反比例函数的解析式。
y
A
Mo
x
2020年10月2日
23
练习 2
1.函数 y =
5 x
的图象在第_二__,四__象限，在每
个象限内，y 随 x 的增大而__增__大_ .
2. 双曲线 y =
1 3x
经过点（-3，_ _91_）
2020年10月2日
6
如图，函数y=k/x和y=－kx+1(k≠0)在同
一坐标系内的图象大致是 （ D）
6y
6y
4
4
2
-5
O
-2
A -4
5x
2
-5
O
-2
B -4
先假设某个函数 5 x 图象已经画好，
再确定另外的是否 符合条件.
6y
4 2
6y
4 2
-5
O
5x
-5
O
5x
-2
C
-4
-2
D
-4
2020年10月2日
数缺形时少直觉，形少数时难入微．
反比例函数的图象与性质2
2020年10月2日
1

x
0
y
0
x
如图，函数y=k/x和y=－kx+1(k≠0)在同 一坐标系内的图象大致是 （ D ）
6
y
6
y
4
4
2
2
-5
O
-2
5
x
-5
O
-2
5
x
A
-4
B
y
6
-4
先假设某个函数 图象已经画好， 再确定另外的是否 符合条件.
6
y
4
4
2
2
-5
O
-2
5
x
-5
O
-2
5
x
-4
C
D
-4
k 3.已知反比例函数 y (k≠0) x
k＞0 当x＜0时，y随x的增大而减小，
则一次函数y=kx-k的图象不经过第 二 象限
y
k＞0 ,-k＜0
o
x
例4:图是反比例函数y= m-5 的图象的一支.根据 x 图象回答下列问题:
(1)图象的另一支在哪个象限?常数m的取值范 围是什么? (2)在这个函数图象的某一支上任取点A(a,b)和 点B(a’,b’).如果a﹥a’,那么b和b’有怎么的大小 y 关系?
则y1与y2的大小关系(从大到小)
x
为 y1 ＞0＞y2
.
A
y
y1
o
x2
x
B
x1
y2
4.已知点 A(-2,y ),B(-1,y ),C(4,y ) 1 2 3 4 y 都在反比例函数 的图象上 , x 则y1、y2与y3的大小关系(从大到小)
为 y3 ＞y1＞y2
.

1、正比例函数
定义：
形如y=kx（k为常数,且k≠0），我们就说y是x的正比例函数。

正比例函数是特殊的一次函数【一次函数的一般形式为y=kx+b（b不为0，k为常数）】。

图象作法:
a.列表(待定系数)
b.描点
c.连线
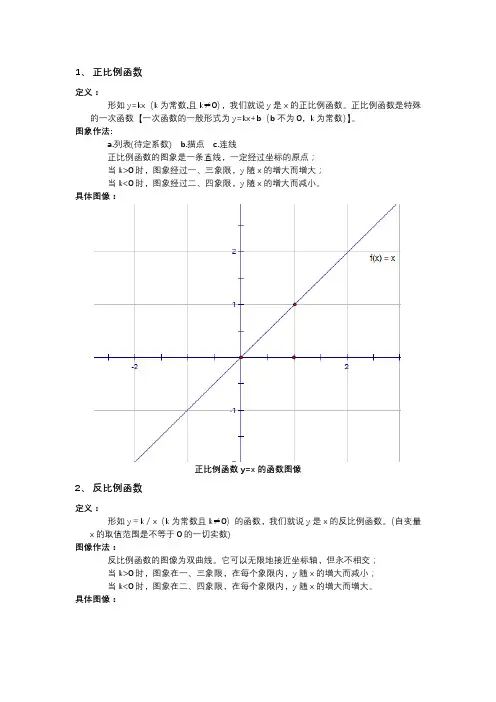
正比例函数的图象是一条直线，一定经过坐标的原点；
当k>0时，图象经过一、三象限，y随x的增大而增大；
当k<0时，图象经过二、四象限，y随x的增大而减小。

具体图像：
正比例函数y=x的函数图像
2、反比例函数
定义：
形如y＝k／x（k为常数且k≠0）的函数，我们就说y是x的反比例函数。

（自变量x的取值范围是不等于0的一切实数)
图像作法：
反比例函数的图像为双曲线。

它可以无限地接近坐标轴，但永不相交；
当k>0时，图象在一、三象限，在每个象限内，y随x的增大而减小；
当k<0时，图象在二、四象限，在每个象限内，y随x的增大而增大。

具体图像：
反比例函数y=1/x的函数图像。

图像形状
反比例函数的图像是两条 关于原点对称的双曲线， 分别位于第一、三象限和 第二、四象限。
图像趋势
当 $x$ 趋近于正无穷或负 无穷时，$y$ 趋近于 0； 当 $x$ 趋近于 0 时，$y$ 趋近于无穷大。
图像与坐标轴关系
反比例函数的图像与坐标 轴没有交点，即不经过任 何象限的角平分线。
反比例函数性质分析
正比例函数性质分析
01
02
03
比例性
正比例函数中，$y$ 与 $x$ 成正比，即当 $x$ 增 大时，$y$ 也随之增大； 当 $x$ 减小时，$y$ 也随 之减小。
直线性
正比例函数的图像是一条 直线，因此具有直线性， 即函数值的变化是均匀的 。
过原点性
正比例函数的图像经过原 点，这意味着当 $x = 0$ 时，$y = 0$。
函数的对称性
如果函数的图像关于某条直线对称，则称该函数具有对称性。例如，二次函数$f(x)=ax^2+bx+c$的图像关于直 线$x=-frac{b}{2a}$对称。
02
正比例函数图像与性质
正比例函数定义及表达式
定义
正比例函数是形如 $y = kx$ （ $k$ 为常数，且 $k neq 0$）的 函数。
反比例函数图像
反比例函数 $y = frac{k}{x}$（$k > 0$）的图像是两条分别位于第一象限 和第三象限的双曲线。这两条曲线关 于原点对称，且随着 $x$ 的增大， $y$ 逐渐减小并趋近于 0。
性质异同点分析
相同点
正比例函数和反比例函数都是关于原点对称的，即它们都是奇函数。
不同点
正比例函数的图像是直线，而反比例函数的图像是双曲线；正比例函数的值随着 $x$ 的增大而增大， 而反比例函数的值随着 $x$ 的增大而减小。

第二部分：正比例 ，反比例函数一、 知识点梳理： （一）正比例函数1、定义：y = kx （k ≠ 0）2、图象：过点（0，0）和（1，k ）的一条直线。

3、性质：当k ＞ 0 时，图象经过一、三象限，y 随x 的增大而增大； 当k ＜ 0 时，图象经过二、四象限，y 随x 的增大而减小。

（二）反比例函数：1、定义：y = xk（k ≠ 0）2、图象：双曲线。

3、性质：（1）当k ＞ 0 时，图象在一、三象限，在每个象限内y 随x 的增大而减小； （2）当k ＜ 0 时，图象在二、四象限，在每个象限内y 随x 的增大而增大。

（三）拓展：1、正比例函数y=kx 过点P （x 0, y 0） 则k=0x y；2、 反比例函数xk y = 过点P （x o , y o ） 则k=x o y o 。

二、知识点检测：1．已知y 是x 的正比例函数，且当51=x 时，1-=y ，则y 关于x 的函数关系式是 ，2．函数x y 91=的图象经过第 象限；当自变量x 的值逐渐增大时，y 的值也 ；3．已知函数xky 21-=在每个象限内自变量x 逐渐增大时，y 的值也随着逐渐增大，则k 的取值范围是 ；4．点P (1，4)、Q (－2，b) 是反比例函数图象上的两个点，则PQ 的长是 ；5．已知反比例函数图象过P (a ，b)，且a 、b 是方程x 2 －4x + 1=0的两个根，则此反比例函数的解析式为 ； 6．甲、乙两地相距180公里，一辆汽车以每小时40公里的速度从甲地开往乙地，已知汽车行驶t 小时后离乙地的距离是S 公里，则S 与t 的函数关系式为 。

三、校正： 1．已知正比例函数图象过点A (2，－4)，则此正比例函数的解析式为 ； 2．已知y 是x 的反比例函数，它的图象经过点（－1，3），那么这个函数的解析式是 ；3．已知正比例函数y=（3k+2）x 的图象经过第一、三象限，则k 的取值范围为 ；4．如果y = (m －2)x + (n + 3)是正比例函数，且图象经过A (1，3)，那么m + 2n = ；5．正比例函数y = kx 的图象和反比例函数y = x1-的图象有一个公共点A 的横坐标为2，这个正比例函数的解析式是 ；6．某车间每月固定成本是15万元，每生产一台仪器需增加成本2万元，则该车间每月的成本数y （万元）与每月生产仪器的台数x 间的函数关系式是 ；四、 典型例题： 1．已知函数y = (m －1)22-m x+ n （m 、n 是实数）（1）当m 、n 取哪些值时，该函数是正比例函数，且函数的图象在第一、三象限？（2）当m 、n 取哪些值时，该函数是反比例函数，且函数的图象经过第二、四象限？（一）处理方法：学生思考，老师针对性的讲评。

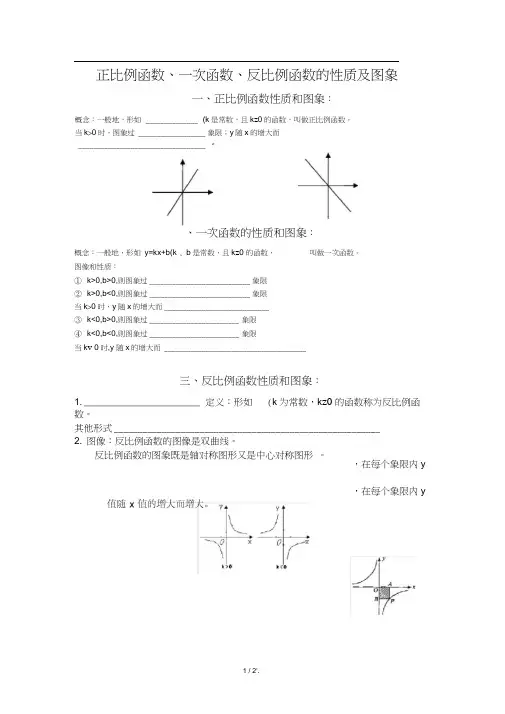
正比例函数、一次函数、反比例函数的性质及图象、一次函数的性质和图象：概念：一般地，形如y=kx+b(k , b是常数，且k z0 的函数，叫做一次函数。

图像和性质：①k>0,b>0,则图象过___________________________ 象限②k>0,b<0,则图象过___________________________ 象限当k>0时，y随x的增大而____________________________③k<0,b>0,则图象过________________________ 象限④k<0,b<0,则图象过________________________ 象限当k v 0时,y 随x的增大而 ______________________________________三、反比例函数性质和图象：1. ______________________ 定义：形如 (k为常数，k z0的函数称为反比例函数。

其他形式________________________________________________________2. 图像：反比例函数的图像是双曲线。

反比例函数的图象既是轴对称图形又是中心对称图形。

，在每个象限内y，在每个象限内y一、正比例函数性质和图象：概念：一般地，形如______________ (k是常数，且k z0的函数，叫做正比例函数。

当k>0时，图象过 __________________ 象限；y随x的增大而__________________________________ 。

3. _________________________________________________ 性质:当k >0时双曲线的两支分别位于_______________________________________值随x值的增大而减小。

正比例函数和反比例函数一、 知识梳理1. 如果变量y 是自变量x 的函数，对于x 在定义域内取定的一个值a ,变量y 的对应值叫做当x=a 时的函数值。

（为了深入研究函数，我们把“y 是x 的函数”用记号y=f(x)表示，这里括号里的x 表示自变量，括号外的字母f 表示y 随x 变化而变化的规律。

f(a)表示当x=a 时的函数值） 2. 函数的自变量允许取值范围，叫做这个函数的定义域。

3. 正、反比例函数的解析式、定义域、图像、性质4. 函数的表示法有三种：列表法，图像法，解析法。

二、 典型题选讲 ●概念辨析1. 在问题研究过程中，可以取不同数值的量叫做＿＿＿＿＿＿＿＿．保持数值不变的量叫做________________表达两个变量之间依赖关系的数学式子称为________________. 2. 写出下列函数的定义域： （1）1y x =+ （2）21y x =- （3）y =(4)y = 3.已知：2()1f x x =-+，(0)f =________,(1)f -=______,(2)f =________. 4.解析式形如(0)y kx k =≠的函数叫做_____________.5.函数3y x =的图像是经过（1，3）和___________的一条____________.当自变量x 的值从小到大逐渐变化时，函数值y 相应地从_________到_______逐渐变化.6.反比例函数的解析式是_________,反比例函数的图像叫_____________.7.已知：反比例函数8y x=，点A （-2，-4）________它的图像上（填“在”或“不在”）.8.反比例函数y x=-的图像的两支在第______象限。

在其各自的象限内，y 随x 的增大而____________.9.函数有三种表示法，分别为_________,__________,__________.10．已知函数12)(+=x x f ，则=)1(f ____________．11．在公式C =2πr 中，C 与r 成 比例.（填“正”或“反”）． 12．函数1-=x y 的定义域为_________________．13．如果13)(-+=x x x f ，那么=)3(f ______________． 14．已知点P （2，1）在正比例函数kx y =的图象上，则k ＝___________． 15．函数y =－2 x 的图象是一条过原点及（2，a ）的直线，则a = ． 16．若正比例函数152)3(--=m x m y 的图像经过二、四象限，则m 的值为 ．17．已知反比例函数2k y x-=，其图象在第一、第三象限内，则k 的取值范围是 ． 18．已知函数xky =的图象不经过第一、三象限， 则kx y -= 的图象经过第 象限．●待定系数法求函数解析式1．若正比例函数经过（2，6），则函数解析式是 ． 2．若反比例函数经过（－2，1），则函数解析式是 ．3．y 与3x 成正比例，当x =8时，y =－12，则y 与x 的函数解析式为___________．4．如果一个等腰三角形的周长为12，那么它的腰长y 与底边x 的函数关系式是 ，自变量x 的取值范围为 ．5．已知反比例函数图像上有一点A ，过点A 做x 轴的垂线，垂足为B ， ΔAOB 的面积为6，则这个反比例函数的解析式为 ．6．已知正比例函数和反比例函数的图象相交于点A （–3，4）和（3，a ）两点，（1）求这两个函数解析式；（2）求a 的值．7、已知21y y y +=，1y 与2x 成正比例，2y 与1-x 成反比例，当x ＝－1时，y ＝3； 当x ＝2时，y ＝－3，（1）求y 与x 之间的函数关系式； （2）当2=x 时，求y 的值。

正比例函数和反比例函数的区别（附图）
一：正比例函数
y=kx(k为常数,且k≠0），我们就说y是x的正比例函数，
正比例函数是特殊的一次函数，一次函数的一般形式为y=kx+b（b不为0，k为常数）。

正比例函数的图象是一条直线，一定经过坐标的原点，
当k>0时，图象经过一、三象限，y随x的增大而增大，
当k<0时，图象经过二、四象限，y随x的增大而减小。

二、反比例函数
y＝k／x(k为常数且k≠0) 的函数，我们就说y是x的反比例函数(自变量x的取值范围是不等于0的一切实数) 。

反比例函数的图像为双曲线，它可以无限地接近坐标轴,但永不相交，
当k>0时，图象在一、三象限,在每个象限内，y随x的增大而减小，
当k<0时，图象在二、四象限,在每个象限内，y随x的增大而增大。

正比例函数和反比例函数的区别（附图）
一：正比例函数
y=kx(k为常数,且k≠0），我们就说y是x的正比例函数，
正比例函数是特殊的一次函数，一次函数的一般形式为y=kx+b（b不为0，k为常数）。

正比例函数的图象是一条直线，一定经过坐标的原点，
当k>0时，图象经过一、三象限，y随x的增大而增大，
当k<0时，图象经过二、四象限，y随x的增大而减小。

二、反比例函数
y＝k／x(k为常数且k≠0) 的函数，我们就说y是x的反比例函数 (自变量x的取值范围是不等于0的一切实数) 。

反比例函数的图像为双曲线，它可以无限地接近坐标轴,但永不相交，
当k>0时，图象在一、三象限,在每个象限内，y随x的增大而减小，
当k<0时，图象在二、四象限,在每个象限内，y随x的增大而增大。

一坐标系内的图象大致是 （D ）
6y
6y
4
4
2
-5
O
-2
A -4
5x
2
-5
O
-2
B -4
先假设某个函数 5 x 图象已经画好，
再确定另外的是否 符合条件.
6y
4 2
6y
4 2
-5
O
5x
-5
O
5x
-2
C
-4
-2
D
-4
3.已知反比例函数 y k (k≠0)
x
当x＜0时，y随x的增大而减小，k＞0 则一次函数y=kx-k的图象不经过第 二 象限
3.已知点 A(x1,y1),B(x2,y2)且x1＜0＜x2 都则在y1与反y比2的例大函小数关y系(xk从(大k＜到0)小的) 图象上,
为 y1 ＞0＞y2 .
y
A
oy1 x2
x1 y2
B
x
4.已知点 A(-2,y1),B(-1,y2),C(4,y3) 都在反比例函数 y 4 的图象上,
的一点,PD⊥x轴于D.则△POD的面积
为1 .
y
P (m,n)
oD
x
2.如图,点P是反比例函数图象上的一 点,过点P分别向x轴、y轴作垂线,若阴 影部分面积为3,则这个反比例函数的
关系式是
y

3 x
.
y
p
N
M ox
例5:如右图点为反比例函数上一点,若图中
阴影部分即三角形AOB的面积为4,求反比
反比例函数的图象与性质2
比较正比例函数和反比例函数的区别
函数 解析式
图象形状
正比例函数

C
A
F E
D B
例题探讨： 例题探讨： 例8.已知直线y=3x+6与x轴、y轴分别相交于点A、B， 8.已知直线y=3x+6与 已知直线y=3x+6 轴分别相交于点A 是坐标原点， AB的长及 AOB的面积 的长及△ 的面积。 点O是坐标原点，求AB的长及△AOB的面积。 例9.已知一次函数的图像经过A（0，-3）、B（1，a）、 9.已知一次函数的图像经过A 已知一次函数的图像经过 ）、B 三点，且函数值y随着x的值增大而减小， C（a，1）三点，且函数值y随着x的值增大而减小， 求这个一次函数的解析式。 求这个一次函数的解析式。 例10.如果关于x的函数y=（m-2）x+m（m≠2）的图像 10.如果关于x的函数y=（ 如果关于 y= x+m（ 2 不经过第三象限， 不经过第三象限，求m的取值范围。 的取值范围。
例题探讨： 例题探讨：
例1.已知一个反比例函数的图像与正比例函数 1.已知一个反比例函数的图像与正比例函数 y=3x的图像都经过点A(a，6) y=3x的图像都经过点A(a， 的图像都经过点A(a （1）求a的值 （2）求反比例函数解析式 （3）求正反比例函数图像的另一个交点B的坐标。 求正反比例函数图像的另一个交点B的坐标。 （4）若一次函数的图像经过A、B两点，求这个一 若一次函数的图像经过A 两点， 次函数的解析式。 次函数的解析式。
双曲线； 双曲线； 两支双曲线无限接 一条直线过点 近于坐标轴， （0，0）和（1，k） 近于坐标轴，但永 远无法达到坐标轴
b〉0,上移 b〈0,下移 平行 ⇔ k相等
正比例函数 y=kx(k≠0) 定义 分 布 k﹥0
0 x 在一、 在一、三象限 y
反比例函数

第21课 正比例函数和反比例函数二、【考点整合举例】正比例函数的概念．用待定系数法求函数解析式的方法．如果正比例函数的图像经过点（2，4），那么这个函数的解析式为 ．如图1，正比例函数图像经过点A ，该函数解析式是 ． 1、如果正比例函数的图像经过点（－2，5），那么这个函数的解析式为 ．2、如果反比例函数的图像经过点（2，4），那么这个函数的解析式为 ．反比例函数)0(>=k xky 的性质及数形结合的能力 在直角坐标系内，从反比例函数)0(>=k xky 的图像上的一点分别作x,y 轴的垂线段，与x 、y 轴所围成的矩形的面积是12，那么该函数解析式是 .1、已知y 与x-1成正比例，且图像经过（2，-3）求y 与x 之间的函数解析式 ___。

2、下列函数中，y 随着x 的增大而减少的是 （ ）（A ） x y 4= （B ）x y 4-= （C ）xy 4=（D ）x y 4-=反比例函数图像的性质及从图上获取信息的能力。

（多选题）在函数y=xk（k>0）的图像上有三点),(111y x A 、),(222y x A 、),(333y x A ，已知3210x x x <<<，则下列各式中，正确的是（ ）（A ）310y y << （B ）130y y << （C ）312y y y << （D ）213y y y <<图1（多选题）若点（－1，y 1），（－2，y 2），（2，y 3）在反比例函数y=－x1的图像上，则下列结论中错误的是 （ ）（A ）321y y y >> （B ）312y y y >> （C ） 213y y y >> （D ）123y y y >> 例1．反比例函数y ＝xk 的图像经过点P （m ，n ），其中m 、n 是一元二次方程x 2＋kx ＋4＝0的两个根，求点P 的坐标．例2. 如图，正比例函数y ＝kx （k ＞0）与反比例函数y ＝x1的图像相交于A 、B 两点，过A 作x 轴的垂线交x 轴于点C ，连结BC ，设△ABC 的面积为S ，求S .(1) 反比例函数x2y =，当x=－2时，y 的值为 （ ） （A ）-2 （B ）-1 （C ）1 （D ）2 (2) 如图，A 、C 是函数y ＝x1的图像上的任意两点，过A 作x 轴的垂线，垂足为B ，过C 作y 轴的垂线，垂足为D ，设Rt △AOB 的面积为S 1，Rt △COD 的面积为S 2，则 （ ）（A ）S 1＞S 2 （B ）S 1＜S 2（C ）S 1＝S 2（D ）S 1和S 2的大小关系不能确定(3) 在同一直角坐标系中，函数y =3x 与y =－x1的图像大致是 （ ）（A ）（B ）（C ）（D ）(4) 已知正比例函数y ＝（2m －1）x 的图像上两点A （x 1，y 1），B （x 2，y 2），当x 1＜x 2时，有y 1＞y 2，那么m 的取值范围是 （ ） （A ）m ＜21（B ）m ＞21 （C ）m ＜2 （D ）m ＞02、填充题：(1) 已知y 与x ＋1成正比例，当x ＝5时，y ＝12，则y 关于x 的函数解析式是________． (2) 一个反比例函数在第二象限的图像如图所示，点A 是图像上任意一点，AM ⊥x 轴，垂足为M ，O 是原点，如果△AOM 的面积为3，那么这个反比例函数的解析式是y ＝___________． (3) 已知反比例函数y ＝（m －1）23m x -的图像在第二、四象限，则m 的值为_________．(4) 点A （a ，b ）、B （a －1，c ）均在函数y ＝x1的图像上若a ＜0，则b ____c （填“＞”或“＜”或“＝”）．1、选择题：（1）已知反比例函数y ＝xm21-的图像上两点A （x 1，y 1）、B （x 2，y 2），当x 1＜0＜x 2时，有y 1＜y 2，则m 的取值范围是 （ ） （A ）m ＜0（B ）m ＞0（C ）m ＜21 （D ）m ＞21 （2）若点（3，4）是反比例函数y ＝kx图像上一点，则此函数图像必经过点 （ ） （A ）（2，6）（B ）（2，－6） （C ）（4，－3） （D ）（3，－4）（3）在同一直角坐标系中，正比例函数y =x 与反比例函数y =－x1的图像大致是 （ ）（A ） （B ） （C ） （D ）2、填充题：(1) 已知函数y ＝kx 的图像经过（2，－6），则函数y ＝xk的解析式可确定为____________． (2) 点A （1，m ）在函数y =2x 的图像上，则点A 关于y 轴的对称的点的坐标是______________． (3) 设有反比例函数y ＝xk 1，（x 1，y 1）、（x 2，y 2）为其图像上的两点，若x 1＜0＜x 2时，y 1＞y 2，则k 的取值范围是________．3、解答题：(1) 正比例函数y=kx 的图像与反正比例函数y=x 21的图像交于A （21，m ），正比例函数y=kx 的图像与反比例函数y=x'k 的图像相交于点B （n,4），求k 和k ’． (2) 已知正比例函数y =kx 与反比例函数y =x3的图像都过A （m ，1）点．求：①正比例函数的解析式；②正比例函数与反比例函数的另一个交点的坐标． (3) 已知正比例函数y ＝4x ，反比例函数y ＝xk ． ①求：k 为何值时，这两个函数的图像有两个交点？k 为何值时，这两个函数的图像没有交点？②这两个函数的图像能否只有一个交点？若有，求出这个交点坐标；若没有，请说明理由．考点一：y ＝2x ；y ＝3x .变式演练：1.y ＝5x 2－；2.y ＝8x.考点二：y ＝12x.变式演练：1.y=-3x+3；2.B.考点三：A 、C . 变式演练：B 、C 、D.（二）综合例题：例1：P 点的坐标为（－2，－2） 例2： S △ABC ＝S △AOC ＋S △BOC ＝1．【双基热身反馈】 1. 选择题：（1） B ；（2）C ；（3）D ；（4）A2、填充题：（1）y ＝2x ＋2；（2）y ＝6x.；（3）－2；（4）＜【复习巩固自测】 1、选择题：（1）C ；（2）A ；（3）D2、填充题：（1）y ＝3x－.；（2）（－1，2）；（3）k ＜－13、解答题：（1）解：∵A(21,m)在y=x 21图像上，∴得m=1， A(21,1)．∵A 又在y=kx 图像上，∴得k=2．∵B （n ，4）在y=2x 图像上，∴4=2·n ，n=2，∴B(2,4)．而B 点又是y=x'k 的图像上，∴4=2'k ，k ’=8．（2）①y ＝1x 3；.②（－3，－1）（3）①解：把y ＝4x 代入y ＝x k ，得 4x 2－k ＝0, ∴ x 2＝4k ；由已知，k ≠0，且（ⅰ）当k ＞0时，有x ＝2k 或x ＝－2k； 所以，两函数图像有两个交点（2k ，2k ）和（2k，－2k ）； （ⅱ）当k ＜0时，4k＜0，x 的值不存在，所以两函数图像没有交点； ②若两个图像只有一个交点，只需方程x 2＝4k 有唯一解，即仅当k ＝0时两个图像只有一个交点．但由已知函数y ＝xk可知，应有k ≠0，所以两个图像只有一个交点是不可能存在的．。