(完整word版)初中水平宽与铅垂高专题

直角坐标系下三角形面积求法——水平宽铅垂高前一阶段我们探讨了一次函数和三角形的面积问题，后台有一些同仁提出了一些宝贵的看法，在此笔者表示感谢。

我们知道对于不规则三角形的面积肯定是用割补法，由此引申出一种水平宽铅垂高的做法，也就是铅垂法。

今天我们来深入地探讨一下铅垂法的做法依据。

我们先从三个顶点都确定的三角形来看。

如图，在直角坐标系中，△ABC三个顶点的坐标为A（1，1）、B （3，4）、C（5，2），试求△ABC的面积。

显然这个三角形属于我们说的所谓不规则三角形（三条边均不和坐标轴平行，且不在坐标轴上），所以我们的基本思路是割补法。

由于此题相对来讲比较简单，我就简单用图形罗列一下各种不同的解法。

方法一：方法二：方法三：方法三是过点B作AC的平行线将不规则的△ABC转化为规则的△ADC从而来求解的过程，其实我们还可以过点A作BC的平行线或者过点C作AB的平行线来进行转化。

鉴于这不是本文研究的重点，另外两种方法在此略过。

方法四：方法五：方法六：方法七：方法八：方法九：方法四、方法五都是在点B处处理，方法四是在点B处作y轴的平行线，方法五是在点B处作x轴的平行线；方法六、方法七都是在点A处处理，方法六是在点A处作y轴的平行线，方法七是在点A处作x轴的平行线；方法八、方法九都是在点C处处理，方法八是在点C处作y轴的平行线，方法九是在点C处作x轴的平行线。

我们再来研究这六个图：如果我们对这六种方法都进行运算、思考，我们就会发现△ABC的面积为图中两个红色线段（一横一竖）乘积的一半。

这就是所谓的铅垂法求面积。

那么如何构造这些线呢？我的看法是选三角形的两个顶点（比如A和B），将AB之间的横坐标体现的横着的线段找出来（图５中的AM），最后一个顶点C作竖着的直线交AB边于点D，此时竖着的线段就是CD，然后利用AM和CD乘积的一半来求解。

或者将AB之间的纵坐标体现的竖着的线段找出来（图6中的AM），过第三个顶点C 作横着的直线交AB边于点D，此时横着的线段就是CD，然后利用AM和CD乘积的一半来求解。

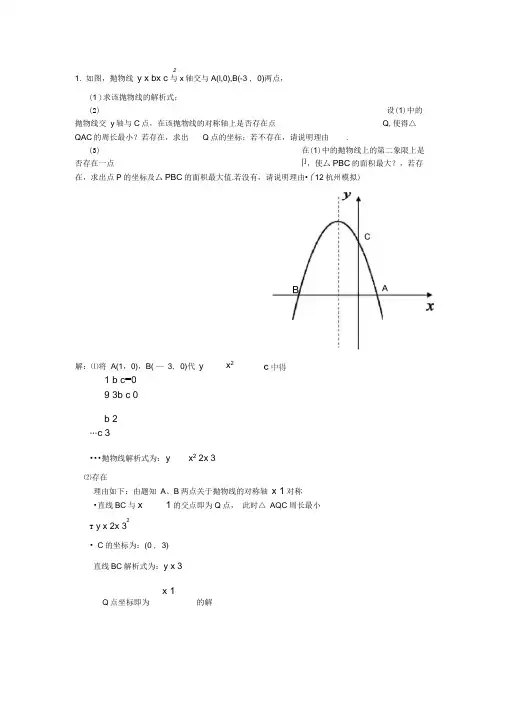
21. 如图，抛物线y x bx c与x轴交与A(l,0),B(-3 , 0)两点，(1 )求该抛物线的解析式；(2)设(1)中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点卩，使厶PBC的面积最大？，若存在，求出点P的坐标及厶PBC的面积最大值.若没有，请说明理由•( 12杭州模拟)解：⑴将A(1，0)，B( —3, 0)代y x21 b c=09 3b c 0b 2…c 3•••抛物线解析式为：y x2 2x 3⑵存在理由如下：由题知A、B两点关于抛物线的对称轴x 1对称•直线BC与x 1的交点即为Q点，此时△ AQC周长最小2T y x 2x 3• C的坐标为：(0 , 3)直线BC解析式为：y x 3x 1Q点坐标即为的解y x 3x 1• y 212•-Q(- 1 , 2)(3)答：存在。

理由如下： 设P 点(X , 22x 3)(3x0) • S BPCS四边形BPCOSBOCS四边形BPCO右S 四边形BPCO 有最大值,BPC 最大,二S四边形 BPCO= SRt BPES 直角梯形PEOC】BE 2 1 =2(x=3(x2 当x 3时,2PE 3)( •I S BPC 最大=-OE(PE OC)2 |)212x 3) -( x)( x2'272x3)S 四边形BPCO 最大值=27 27272当x 3时，2一 3 •••点P 坐标为(一, 2 1 •备用答案: 2x 15 1579a 3a解：⑴将(31), (0,-)代入得:解得•••抛物线的解析式为：y 1x2 lx 22 2⑵过B作BE X x轴于E,则E ( -3, 0),易证△ BE3A COA•BE= AO = 2 CO = 1• C (- , 0)(3)延长BC至U P,使CP= BC,连结AP,则厶ACP为以AC为直角边的等腰直角三角形过P作PF丄x轴于F,易证△ BEC^^ DFC•CF= CE= 2 PF= BE= 1•- P (1, -1)将(1, -1)代入抛物线的解析式满足若CAP 90 , AC = AP则四边形ABCP为平行四边形过P作PG丄y轴于G,易证△ PGA SA CEB•PG= 2 AG = 1•P (2, 1)在抛物线上存在P (1 , -1), (2 , 1)满足条件2. (本小题满分12分)如图①， 已知抛物线y ax 2 bx 3 (a 丰0)与x 轴交于点A(1, 0)和点B (- 3, 0)，与 y 轴交于点C . (1) 求抛物线的解析式；(2) 设抛物线的对称轴与 X 轴交于点N ，问在对称轴上是否存在点 P,使厶CNP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由.2(1)设每年的平均增长率为 x,144(1+x) =225,x=1/4 或x=-9/4 (舍去)225 X(1 + 1/4)=281 (1)设可建室内车位个，露天车位 b 个，3a < b w 4.5a 50 125 6000a+2000b=250000w a w36a=17,b=74; a=18,b=71; a=19,b=68; a=20,b=65 24.(本小题满分12分)2如图①， 已知抛物线y ax bx 3 (a 丰0)与x 轴交于点A(1, 0)和点B (— 3, 0),与(3) 如图②，若点E 为第三象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大15(2)值，并求此时E 点的坐标.08y 轴交于点C .2⑴ y=x +2x-3— — 5 (2) P(-1, .10 ),P(-1,- , 10 ),P(-1,-6),P(-1,--) 32(3) S=1/2 X 3 X(-x -2x+3)+ 1/2 X 3 X(-x)2S=-3/2(x+3/2)+63/8E(-3/2,-15/4)3. （本小题满分12分）（原创）2y x -2x-4与直线y x 交于点A 、B ，M 是 抛物线上一个动点，连接 0M 。

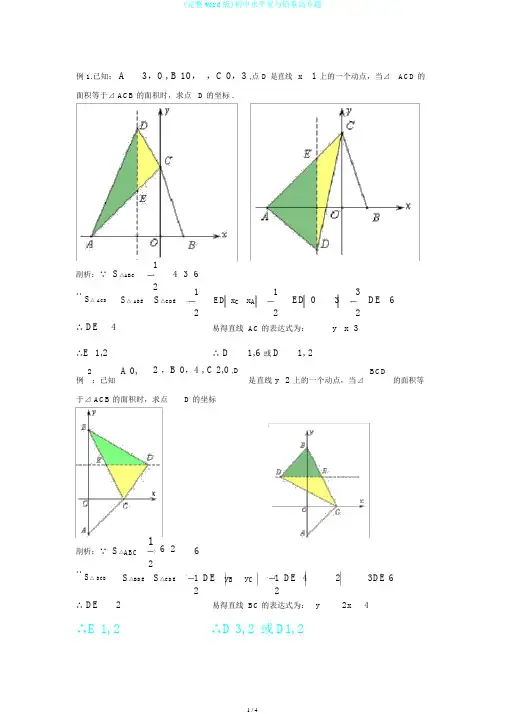
例 1.已知： A3，0 , B 10， ，C 0，3 ,点 D 是直线 x 1上的一个动点，当⊿ACD 的面积等于⊿ ACB 的面积时，求点 D 的坐标 .S △ABC1剖析：∵4 3 6211 3∴S △ ACDS △ ADES △CDEx AED 0 DE 6ED x C 2 322∴ DE 4易得直线 AC 的表达式为： y x 3∴E 1,2∴ D1,6 或D 1, 22 A 0, 2 ，B 0，4 , C 2,0 ,D是直线 y 2 上的一个动点，当⊿BCD的面积等例 ：已知于⊿ ACB 的面积时，求点 D 的坐标剖析：∵ S △ABC16 26211∴S △ BCDS △BDE S △CDEDE y B y C DE 4 23DE 622∴ DE 2易得直线 BC 的表达式为： y 2x 4∴E 1,2 ∴D 3,2 或D 1,21.如图，一次函数y 1x 2 分别与x轴、 y 轴交于点A、B两点，在平面直角坐标系2中，有一点 C 1,m，当△ ABC 的面积为5 时，求点 C 的坐标2.如图，在平面直角坐标系中，O 为坐标原点，直线l1与 x 轴交与点A(-2，0)，与y轴交于点 B，与直线l2：y 315， D 为直线l2与x轴的交点x交于点 C 1,m447（ 1）求直线l1的表达式；（2）在直线 AB 上找一点 Q，使得S△QCD S△ABO,求Q点的2坐标 .3. 如图，在平面直角坐标系中，一次函数1x 2 与x轴、 y 轴分别交于点A、B 两y2点，以线段 AB 为边在第一象限内作等腰直角三角形ABC ，且∠ BAC=90 °，（ 1）求点 C 的坐标(2) 在平面直角坐标系中有一点P 1, m ，且△ABP的面积等于△ABC的面积，求m的值.4. 如图，在直角梯形AOBC中， AC∥ OB，且 OB=6， AC=5， OA=4.（1）求 B、 C 两点的坐标；（2）以 O、 A、B、 C 中的三点为极点可构成哪几个不一样的三角形？（ 3）能否在边AC和 BC（含端点）上分别存在点M和点 N，使得△MON的面积最大时，它的周．．．长还最短？若存在，说明原因，并求出这时点M、 N 的坐标；若不存在，为何？5.如图，已知二次函数y x22x 3 交 x 轴于A点，交y轴于B点，点C是线段OA 上不一样于A 和O 的点，过C 作x轴的垂线，交二次函数的图象与M, 交AC于 N,求⊿ AMB 面积的最大值6.如图，抛物线yx24x 5 的图象经过点A和B（ 1）求点 A 和 B 的坐标；（ 2）抛物线与x轴的另一个交点是C， P 是线段 OC上的一点，过点P 作 PH⊥x轴，与抛物线交于H 点，交BC于E 点，如直线BC把⊿ PCH分红面积1： 3 的两部分，恳求出P点的坐标．。

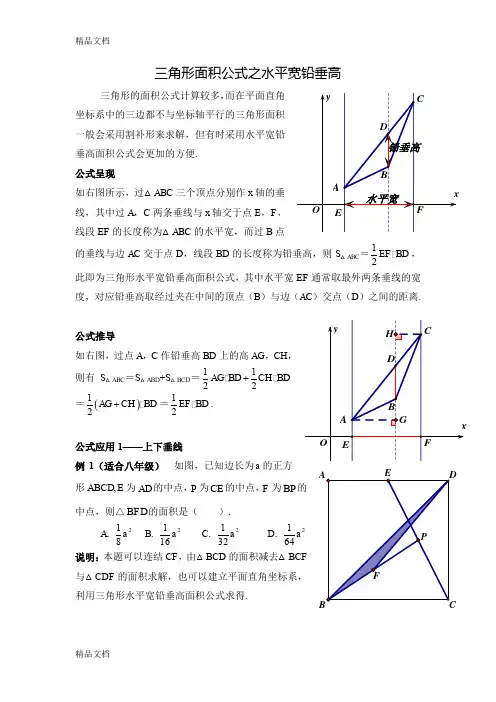
精品文档三角形的面积公式计算较多，垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 线，其中过A ，C 两条垂线与x 轴交于点E ，F 线段EF 的长度称为△ABC 的水平宽，而过B 的垂线与边AC 交于点D ，线段BD BD ，通常取最外两条垂线的宽度，对应铅垂高取经过夹在中间的顶点（B ）之间的距离.公式推导如右图，过点A ，C 作铅垂高BD 上的高AG ，则有S △ABC ＝S △ABD +S △BCD ＝1122AG BD CH +＝()12AG CH BD +＝12EF BD .公式应用1——上下垂线例1（适合八年级） 如图，已知边长为a 形E ABCD ,为AD 的中点，P 为CE 的中点，F 为中点，则△BFD 的面积是（ ）.A .281a B . 2161a C . 2321a D .说明：本题可以连结CF ，由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得.精品文档解析：不妨以B 为原点，BC 为x 轴，BA 为y 轴建立平面直角坐标系，则点C 坐标为（a ，0），点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ）， ∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==.公式应用2——左右垂线例2（适合八年级） 如图，直线1y x =+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a 的值.说明：本题常见解法有三，一是连结OP ，△ABP 的面积＝△AOB 面积+△BOP 面积－△AOP 面积，然后用a 的代数式表示，与Rt △ABC相等列方程求解；二是将点C 沿AB 翻折到C ’位置，则△ABC △ABC ’面积相等，若△ABP 的面积与Rt △ABC P精品文档相等，则可得PC ’//AB ，因此，可以由点A ，C 坐标先求C ’坐标，再根据AB 的斜率与点C ’坐标求直线PC ’的解析式，将点P 纵坐标代入，即可求a 的值. 三是考虑水平宽铅垂高公式来计算，但如果从A ，B ，P 三点向x 轴作垂线，较为复杂，不妨换个角度应用公式，即从A ，B ，P 向y 轴作垂线（即左右方向作垂线）解析：过线，则OB 而PE 度）由AB OB ＝1，而P 的纵坐标为12，所以E 为AB 的中点， 所以PE ＝-a +2， 从而有1122122a ⎛⨯⨯=⨯⨯- ⎝⎭ ， 解得4a =-.公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有12EF CG . 简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH -＝12EF CG .精品文档说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）. 例3（适合九年级） 如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y 轴翻折，点A 落到点C ，抛物线过点B ，C 和D （3，0）． （1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 在坐标轴上，以点N ，B ，D 为顶点的三角形与△MCD 相似，求所有满足条件的点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6？若存在，求出点P 的坐标；若不存在，说明理由．（4）点Q 是抛物线对称轴上一动点，是否存在点Q 使得CQ BQ -的值最大，若存在，请直接写出点Q解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD＝3，铅垂高为PE ＝224333x x x x x -++-=-； 当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.精品文档当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6.解后：从以上几例可以看到，灵活运用水平宽与铅垂高公式，可以有效解决三角形面积问题，尤其是在例3，可以将P 点的两种不同的位置分类统一为PE 长（绝对值）问题求解，可以有效回避原本点P 在BD 上方时，几何法要构造高等繁杂作法，使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。

初中水平宽与铅垂垂直专题
1. 水平宽的定义与性质
- 水平宽是指两个点在平面上的横坐标之差。

对于坐标系中的
两点A(x₁, y₁)和B(x₂, y₂)，水平宽的计算公式为：水平宽 = |x₂
- x₁|。

2. 铅垂的定义与性质
- 铅垂是指一条线段与平面上一点的垂直线段。

对于平面上的
一点P(x, y)及一线段AB，线段AB与点P的铅垂为垂直于线段AB
的线段，记作垂直线段CD。

3. 水平宽与铅垂的关系
- 若两个点A(x₁, y₁)和B(x₂, y₂)在平面上且满足水平宽为0，则点A和点B在同一垂直铅垂线上。

- 若点A(x₁, y₁)在直线l上，且点B(x₂, y₂)在直线l上，且
满足水平宽为0，则点A和点B在同一垂直铅垂线上。

4. 练题
1. 已知点A(2, 5)和点B(8, 5)，求点A和点B之间的水平宽是多少？
2. 已知点P(-3, 7)在直线l上，点Q(5, 7)也在直线l上，求点P 和点Q之间的水平宽是多少？
3. 在坐标系中，点C(4, 1)和点D(4, -3)是否在同一垂直铅垂线上？
以上是关于初中水平宽与铅垂垂直专题的简介。

通过学习与练习题目，希望能够帮助学生更好地理解和掌握水平宽与铅垂垂直的概念和性质。

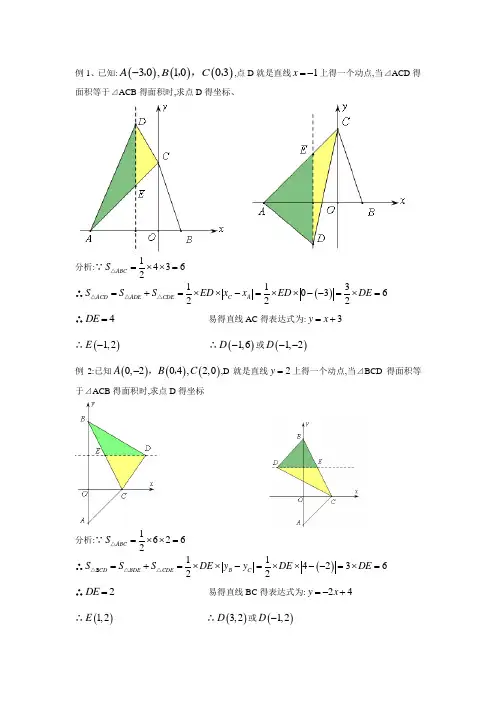
例1、已知:()()()30,1003A B C -，，，，,点D 就是直线1x =-上得一个动点,当⊿ACD 得面积等于⊿ACB 得面积时,求点D 得坐标、分析:∵14362ABC S =⨯⨯=△ ∴()113036222ACD ADE CDE C A S S S ED x x ED DE =+=⨯⨯-=⨯⨯--=⨯=△△△ ∴4DE = 易得直线AC 得表达式为:3y x =+ ∴()1,2E - ∴()1,6D -或()1,2D -- 例2:已知()()()0,204,2,0A B C -，，,D 就是直线2y =上得一个动点,当⊿BCD 得面积等于⊿ACB 得面积时,求点D 得坐标分析:∵16262ABC S =⨯⨯=△ ∴()11423622CD BDE CDE B C S S S DE y y DE DE =+=⨯⨯-=⨯⨯--=⨯=△B △△ ∴2DE = 易得直线BC 得表达式为:24y x =-+ ∴()1,2E ∴()3,2D 或()1,2D -1、如图,一次函数122y x =-+分别与x 轴、y 轴交于点A 、B 两点,在平面直角坐标系中,有一点C ()1,m ,当△ABC 得面积为5时,求点C 得坐标2、如图,在平面直角坐标系中,O 为坐标原点,直线1l 与x 轴交与点A(-2,0),与y 轴交于点B,与直线231544l y x =-+：交于点C ()1,m ,D 为直线2l 与x 轴得交点 (1)求直线1l 得表达式;(2)在直线AB 上找一点Q,使得72QCD S S =△△ABO ,求Q 点得坐标、3、如图,在平面直角坐标系中,一次函数122y x =-+与x 轴、y 轴分别交于点A 、B 两点, 以线段AB 为边在第一象限内作等腰直角三角形ABC,且∠BAC=90°,(1)求点C 得坐标(2)在平面直角坐标系中有一点()1,P m -,且△ABP 得面积等于△ABC 得面积,求m 得值、4、如图,在直角梯形AOBC 中,AC ∥OB,且OB=6,AC=5,OA=4、(1)求B 、C 两点得坐标;(2)以O 、A 、B 、C 中得三点为顶点可组成哪几个不同得三角形？(3)就是否在边AC 与BC(含端点)上分别存在点M 与点N,使得△MON 得面积最大时．．．,它得周长还最短？若存在,说明理由,并求出这时点M 、N 得坐标;若不存在,为什么？5、如图,已知二次函数223y x x =--+交x 轴于A 点,交y 轴于B 点,点C 就是线段OA上不同于A 与O 得点,过C 作x 轴得垂线,交二次函数得图象与M,交AC 于N,求⊿AMB面积得最大值6、如图,抛物线245y x x =--+得图象经过点A 与B(1)求点A 与B 得坐标;(2)抛物线与x 轴得另一个交点就是C,P 就是线段OC 上得一点,过点P 作PH ⊥x 轴,与抛物线交于H 点,交BC 于E 点,如直线BC 把⊿PCH 分成面积1:3得两部分,请求出P 点得坐标.。

铅锤高与水平宽之二次函数与面积问题综合练习题例1：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可得出一种计算三角形面积的新方法：解答下列问题：如图2，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），交y轴于点B．（1）求抛物线和直线AB的解析式；（2）点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C 时，求△CAB的铅垂高CD及S△CAB；练习1：已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．例2.抛物线y=﹣x2+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．（1）求抛物线的函数表达式；（2）若点P在抛物线上，且S△AOP=4S BOC，求点P的坐标；（3）如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ 长度的最大值．:练习2：在平面直角坐标系中，已知抛物线经过:A（-4,0），B（0,-4），C（2,0）三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．练习3：抛物线y=mx 2-11mx+24m （m ＜0）与x 轴交于B 、C 两点（点B 在点C 的左侧），抛物线另有一点A 在第一象限内，且∠BAC=90°．（2）连接OA ，将△OAC 沿x 轴翻折后得△ODC ，当四边形OACD 是菱形时，求此时抛物线的解析式； （3）如图2，设垂直于x 轴的直线l：x=n 与（2）中所求的抛物线交于点M ，与CD 交于点N ，若直线l 沿x 轴方向左右平移，且交点M 始终位于抛物线上A 、C 两点之间时，试探究：当n 为何值时，四边形AMCN 的面积取得最大值，并求出这个最大值．。