物理化学课件及考试习题 试卷 答案第四次习题课(第九章化学动力学基础).

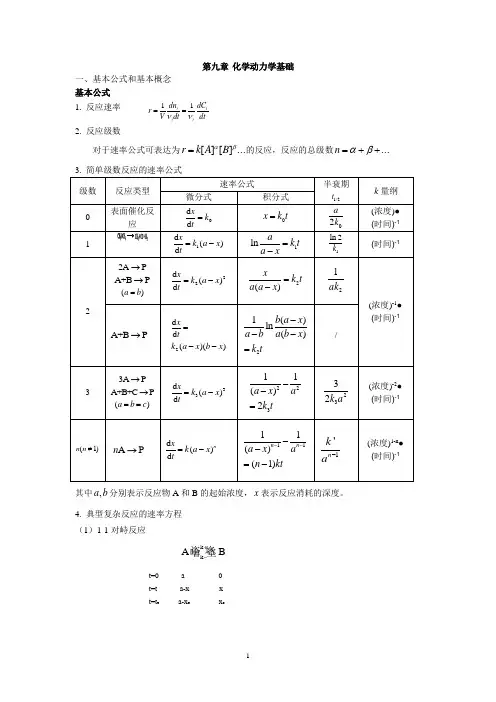
第九章 化学动力学基础一、基本公式和基本概念 基本公式 1. 反应速率 11i ii i dn dC r V dtdtνν==2. 反应级数对于速率公式可表达为...][][βαB A k r =的反应，反应的总级数...++=βαn 3. 简单级数反应的速率公式 级数 反应类型 速率公式半衰期 1/2tk 量纲微分式积分式0 表面催化反应0d d x k t =0x k t = 02a k (浓度)● (时间)-1 11d ()d x k a x t=-1lna k t a x=-1ln 2k(时间)-122A P→A +B P →()a b =22d ()d x k a x t=-2()x k t a a x =-21ak(浓度)-1●(时间)-1A +B P →2d d ()()xtk a x b x =--21()ln()b a x a b a b x k t---=/33A P→A +B +C P→()a b c ==33d ()d x k a x t=-22311()2a x a k t --=2332k a(浓度)-2● (时间)-1(1)n n ≠A P n →d ()d nx k a x t=-1111()(1)n n a x an kt----=-1'n k a-(浓度)1-n ● (时间)-1其中,a b 分别表示反应物A 和B 的起始浓度，x 表示反应消耗的深度。

4. 典型复杂反应的速率方程 （1）1-1对峙反应k k A B +-t=0 a 0 t=t a-x x t=t e a-x e x e速率方程： ()kk te e x x x e +--+-=（2）平行反应最简单的平行反应是由两个一级基元反应组成的平行反应：x=x 1+x 2速率方程：tk k aex a )(21+-=-产物B 和C 的浓度比由竞争反应的速率决定：2121k k x x = （3）连续反应最简单的连续反应是两个单向连续的一级反应：C B A kk −→−−→−21t=0 a 0 0 t=t x y z 速率方程：1k tx ae-=)(21121tk tk eek k a k y ----=]1[21121122tk tk ek k k ek k k a z ---+--=中间产物B 的浓度在反应过程中出现极大值：122)(21k k k m k k a y -=，出现极大值的时间为：2121)ln(k k k k tm-=5. 温度对反应速率的影响 （1）阿累尼乌斯经验公式2ln RTE dTk d a =阿累尼乌斯公式的指数函数式: RTE a Aek -=k 1k 2A a-xCx 2 B x 1（2）阿累尼乌斯活化能基元反应的活化能是活化分子的平均能量与所有分子平均能量之差。

第九章统计热力学基础一、基本公式玻尔兹曼公式：Ωk S ln =玻尔兹曼分布：∑--=ikTi kTi i e g e g N n //εε两个能级上的粒子数之比kT j kTi j i ji e g e g n n //εε--=分子的配分函数：kT ii ie g q /ε-∑=（能级求和）kTjj eq /ε-∑=（量子态求和）能级能量公式：平动⎪⎪⎭⎫ ⎝⎛++=22222228c n b n a n m h z y x i ε转动Ih J J r 228)1(πε+=振动νεh v v⎪⎭⎫⎝⎛+=21平动配分函数：一维L h mkT q t 2122⎪⎭⎫ ⎝⎛=π；二维A h mkT q t ⎪⎭⎫ ⎝⎛=22π；三维Vh mkT q t 2322⎪⎭⎫ ⎝⎛=π转动配分函数：线型分子rr ΘTh IkT q σσπ==228，转动特征温度Ik h Θr 228π=非线型分子zy x r I I I hkT q 3232)2(8σππ=振动配分函数：双原子分子T ΘTΘkT h kT h v v v e e e e q /2//2/11-----=-=νν，振动特征温度v Θh h ν多原子线型∏-=---=531/2/1n i kTh kT h v i ie e q νν多原子非线型∏-=---=631/2/1n i kT h kTh v iie e q νν电子运动配分函数kTe e j q /0)12(ε-+=原子核运动配分函数kT n e e S q /0)12(ε-+=热力学函数与配分函数的关系N q kT A ln -=（定位）!ln N q kT A N -=（非定位）N V N T q NkT q k S ,ln ln ⎪⎭⎫ ⎝⎛∂∂+=（定位）N V N T q NkT N q k S ,ln !ln ⎪⎭⎫ ⎝⎛∂∂+=（非定位）N T N V q NkTV q kT G ,ln ln ⎪⎭⎫ ⎝⎛∂∂+-=（定位）N T N V q NkTV N q kT G ,ln !ln ⎪⎭⎫ ⎝⎛∂∂+-=（非定位）NV T q NkT U ,2ln ⎪⎭⎫ ⎝⎛∂∂=N T N V V q NkTV T q NkT H ,,2ln ln ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=NT T q NkT p ,ln ⎪⎭⎫ ⎝⎛∂∂=VN V V T q NkT T c ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂∂∂=,2ln 4.设有一个极大数目的三维平动子组成的粒子体系，运动于边长为a 的立方容器中体系的体积、粒子质量和温度有如下关系：kT ma h 10.0822=，求处于能级22149ma h =ε和222427mah =ε上粒子数目的比值是多少？解：kTkTe g e g n n 212121εε--=kT ma h ma h 8.18184922221===ε18222=++z y x n n n 31=g kT ma h 7.2827221==ε42=g 84.1437.28.121==--e e n n 5.将N 2气在电弧中加热，从光谱中观察到处于第一激发振动态的相对分子数26.001===ννN N ，式中ν为振动量子数N ν=0为基态占有的分子数，N ν=1为第一激发振动态占有的分子数，已知N 2的振动频率ν=6.99×1013s -1。

物理化学习题解答(九)习题p109~1161解：(1) Pt︱H2(p H2)︱HCl(a)︱Cl2(p Cl2)︱Pt正极：Cl2(p Cl2)+ 2e-→2Cl-(a)负极：H2(p H2) –2e-→2H+(a)电池反应：H2(p H2) + Cl2(p Cl2)==2HCl(a) (2) Pt︱H2(p H2)︱H+(a H+)‖Ag+(a Ag+)︱Ag(s) 正极：Ag+(a Ag+)+ e-→Ag(s)负极：H2(p H2) –2e-→2H+(a H+)电池反应：H2(p H2) + Ag+(a Ag+)==2H+(a H+)+ Ag(s)(3) Ag(s)︱AgI(s)︱I-(a I-)‖Cl-(a Cl-)︱AgCl(s)︱Ag(s)正极：AgCl(s) + e-→Ag(s) + Cl-(a Cl-)负极：Ag(s) + I-(a I-)– e-→AgI(s)电池反应：AgCl(s) + I-(a I-)==AgI(s) + Cl-(a Cl-)(4) Pb(s)︱PbSO4(s)︱SO42-(a SO42-)‖Cu2+(a Cu2+)︱Cu(s)正极：Cu2+(a Cu2+) + 2e-→Cu(s)负极：Pb(s) + SO42-(a SO42-)–2e-→PbSO4(s)电池反应：Pb(s) + Cu2+(a Cu2+) + SO42-(a SO42-)==PbSO4(s) + Cu(s)(5) Pt︱H2(p H2)︱NaOH(a)︱HgO(s)︱Hg(l)正极：HgO(s) + H2O (l)+ 2e-→Hg(l) + 2OH-(a OH-)负极：H2(p H2)+ 2OH-(a OH-) –2e-→2H2O(l)电池反应：HgO(s) + H2(p H2)==Hg(l)+H2O(l) (6) Pt︱H2(p H2)︱H+(a H+)︱Sb2O3(s)︱Sb(s) 正极：Sb2O3(s) + 6H+(a H+)+ 6e-→2Sb(s) + 3H2O(l)负极：H2(p H2) –2e-→2H+(a H+)电池反应：Sb2O3(s) + 3H2(p H2) ==2Sb(s) + 3H2O(l)(7) Pt︱Fe3+(a1)，Fe2+(a2)‖Ag+(a Ag+)︱Ag(s)正极：Ag+(a Ag+)+ e-→Ag(s)负极：Fe2+(a2) – e-→ Fe3+(a1)电池反应：Ag+(a Ag+) + Fe2+( a2)==Fe3+( a1)+Ag(s)(8) Na(Hg)(a am)︱Na+(a Na+)‖OH-(a OH-)︱HgO(s)︱Hg(l)正极：HgO(s) + H2O (l)+ 2e-→Hg(l) +2OH-(a OH-)负极：2Na(Hg)(a am) –2e-→2Na+(a Na+) + 2Hg(l)电池反应：2Na(Hg)(a am) + HgO (s) + H2O(l)==2 Na+(a Na+) + 2OH-(a OH-) + 3Hg(l)2解：(1)AgCl(s)==Ag+(a Ag+) + Cl-(a Cl-)电池：Ag(s)︱Ag+(a Ag+)‖Cl-(a Cl-)︱AgCl(s)︱Ag(s)正极：AgCl(s) + e-→Ag(s) + Cl-(a Cl-)负极：Ag(s)–e-→Ag+(a Ag+)电池反应：AgCl(s)==Ag+(a Ag+) + Cl-(a Cl-) (2)AgCl(s) + I-(a I-) ==AgI(s) + Cl-(a Cl-)电池：Ag(s)︱AgI(s)︱I-(a I-)‖Cl-(a Cl-)︱AgCl(s)︱Ag(s)正极：AgCl(s) + e-→A g(s) + Cl-(a Cl-)负极：Ag(s) + I-(a I-)– e-→AgI(s)电池反应：AgCl(s) + I-(a I-) ==AgI(s) + Cl-(a Cl-)(3) HgO(s) + H2(p H2)==Hg(l)+H2O(l)电池：Pt(s)︱H2(p H2)︱NaOH(a)︱HgO(s)︱Hg(l)正极：HgO(s) + H2O(l) + 2e-→Hg(l) + 2OH-(a)负极：H2(g) + 2OH-(a) –2e-→2H2O(l)电池反应：HgO(s) + H2(p H2)→Hg(l) + H2O(l) (4) Fe2+(a Fe2+) + Ag+(a Ag+)== Fe3+(a Fe3+) + Ag(s)电池：Pt(s)︱Fe3+(a Fe3+)，Fe2+( a Fe2+)‖Ag+(a Ag+)︱Ag(s)正极：Ag+(a Ag+)+ e-→Ag(s)负极：Fe2+( a Fe2+) – e-→ Fe3+( a Fe3+)电池反应：Fe2+(a Fe2+)+Ag+(a Ag+)== Fe3+( a Fe3+) + Ag(s)(5) 2 H2(p H2) + O2(p O2)==2H2O(l)电池：Pt︱H2(p H2)︱H+(a H+)︱O2(p O2)︱Pt(s) 正极：O2(p O2) + 4H+(a H+) + 4 e-→2H2O(l)负极：2H2(p H2) – 4e-→4H+(a H+)电池反应：2 H2(p H2) + O2(p O2)==2H2O(l) (6) Cl2(p Cl2) + 2I-(a I-)==I2(s)+2Cl-(a Cl-)电池：Pt︱I2(s))︱I-(a I-)‖Cl-(a Cl-)︱Cl2(p Cl2)︱Pt正极：Cl2(p Cl2) + 2e-→2Cl-(a Cl-)负极：2I-(a I-)–2e-→ I2(s)电池反应：Cl2(p Cl2) + 2I-(a I-)==I2(s)+2Cl-(a Cl-) (7) H2O(l)== H+(a H+) + OH-(a OH-)电池：Pt(s)︱H2(p H2)︱H+(a H+)‖OH-(a OH-)︱H2(p H2)︱Pt(s)正极：2H2O(l) + e-→2H2(p H2) + 2OH-(a OH-) 负极：H2(p H2)–2e-→ 2H+(a H+)电池反应：H2O(l)== H+(a H+) + OH-(a OH-) (8) Mg(s) + 1/2O2(g) + H2O(l)== Mg(OH)2(s) 电池：Mg(s)︱Mg(OH)2(s)︱OH-(a OH-)︱O2(p O2)︱Pt(s)正极：1/2O2(g) + H2O(l) + 2e-→ 2OH-(a OH-) 负极：Mg(s) + 2OH-(a OH-)– 2e-→Mg(OH)2(s) 电池反应：Mg(s) + 1/2O2(g) + H2O(l)== Mg(OH)2(s)(9) Pb(s) + HgO(s)==Hg(l) + PbO(s)电池：Pb(s)︱PbO(s)︱OH-(a OH-)HgO(s)︱Hg(l)正极：HgO(s) + H2O(l) + 2e-→ Hg(l) + 2OH-(a OH-)负极：Pb(s) + 2OH-(a OH-) –2e-→PbO(s) + H2O(l)电池反应：Pb(s) + HgO(s)==Hg(l) + PbO(s) (10) Sn2+(a Sn2+) + Tl3+(a Tl3+) == Sn4+(a Sn4+) + Tl+(a Tl+)电池：Pt(s)︱Sn2+(a Sn2+)，Sn4+(a Sn4+)‖Tl3+(a Tl3+)，Tl+(a Tl+)︱Pt(s)正极：Tl3+(a Tl3+) + 2e-→ Tl+(a Tl+)负极：Sn2+(a Sn2+) –2e-→Sn4+(a Sn4+)电池反应：Sn2+(a Sn2+) + Tl3+(a Tl3+) == Sn4+(a Sn4+) + Tl+(a Tl+)15解：Fe(s) + Cd2+(aq)==Cd(s)+Fe2+(aq)E=Eө– RT/2F×ln{[ Fe2+]/[Cd2+]}(1) E=φөcd2+/Cd–φөFe2+/Fe- RT/2F×ln{[ Fe2+]/[Cd2+]}=-0.40 +0.44–0.0592/2lg{0.1/0.1}=0.04>0反应能自发向右进行，故金属Fe首先被氧化。

第二章 热力学第一定律2.1 1mol 理想气体在恒定压力下温度升高1℃，求过程中系统与环境交换的功。

解：理想气体n = 1mol对于理想气体恒压过程,应用式（2.2.3）W =－p amb ΔV =－p(V 2-V 1) =－(nRT 2-nRT 1) =－8.314J2.2 1mol 水蒸气(H 2O,g)在100℃,101.325kPa 下全部凝结成液态水。

求过程的功。

假设：相对于水蒸气的体积，液态水的体积可以忽略不计。

解: n = 1mol恒温恒压相变过程,水蒸气可看作理想气体, 应用式（2.2.3）W =－p amb ΔV =－p(V l -V g ) ≈ pVg = nRT = 3.102kJ2.3 在25℃及恒定压力下，电解1mol 水(H 2O,l)，求过程的体积功。

H 2O(l) ＝ H 2(g) + 1/2O 2(g) 解: n = 1mol恒温恒压化学变化过程, 应用式（2.2.3）W=－p amb ΔV =－(p 2V 2-p 1V 1)≈－p 2V 2 =－n 2RT=－3.718kJ2.4 系统由相同的始态经过不同途径达到相同的末态。

若途径a 的Q a =2.078kJ,Wa=－4.157kJ ；而途径b 的Q b =－0.692kJ 。

求W b .解: 热力学能变只与始末态有关,与具体途径无关,故 ΔU a = ΔU b由热力学第一定律可得 Qa + Wa = Q b + W b ∴ W b = Q a + W a －Q b = －1.387kJ2.5 始态为25℃，200 kPa 的5 mol 某理想气体，经途径a ，b 两不同途径到达相同的末态。

途经a 先经绝热膨胀到 -28.47℃，100 kPa ，步骤的功；再恒容加热到压力200 kPa 的末态，步骤的热。

途径b 为恒压加热过程。

求途径b 的及。

解：先确定系统的始、末态3111061902000001529831485m ...P nRT V =××==32101601000005824431485m ...P nRT V V =××=== kJ .kJ )..(Q W U Δa a 85194225575=+=+=－对于途径b ，其功为kJ .J ..V Δp W b 932706190101602000001－）－（－－===根据热力学第一定律2.6 4mol 某理想气体，温度升高20℃, 求ΔH －ΔU 的值。

物理化学（二）练习1（化学动力学）2014级一、选择题( 共15题)1-1. 反应A k1B (I)；Ak2D (II)，已知反应I 的活化能E1大于反应II 的活化能E2，以下措施中哪一种不能改变获得B 和D 的比例？(A) 提高反应温度(B) 延长反应时间(C) 加入适当催化剂(D) 降低反应温度1-2. 如果某反应的△r H m= 100ｋJ·mol-1，那么活化能E a将：(A) E a≠100ｋJ·mol-1(B) E a≥100ｋJ·mol-1(C) E a≤100ｋJ·mol-1(D) 都可以1-3. 2A k1产物上述反应对A 为二级，下列何者对时间作图可得一直线，且直线斜率等于速率常数k？(A) 2[A](B) [A]2(C) 1/[A](D) 1/[A]21-4. 某反应进行时，反应物浓度与时间成线性关系，则此反应的半衰期与反应物初始浓度：(A) 成正比(B) 成反比(C) 平方成反比(D) 无关1-5.此反应的速率方程为：(A) r = k c B(B) r = k c A c B(C) r = k c A(c B)2(D) r = k c A1-6.400 K 时，某气相反应的速率常数k p= 10-3(kPa)-1·s-1，如速率常数用k C表示，则k C应为：(A) 3.326 (mol·dm-3)-1·s-1(B) 3.0×10-4 (mol·dm-3)-1·s-1(C) 3326 (mol·dm-3)-1·s-1(D) 3.0×10-7 (mol·dm-3)-1·s-11-7. 均相反应A + B k1C +D ， A + Bk2E +F 在反应过程中具有∆[C]/∆[E] = k1/k2的关系，∆[C]，∆[E] 为反应前后的浓差，k1，k2是反应(1)，(2)的速率常数。