趋势剔除法求季节指数的计算案例(优选材料)

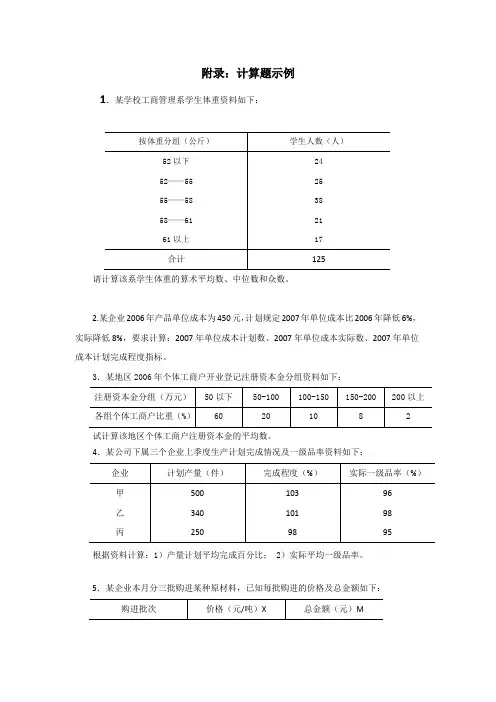
附录：计算题示例1．某学校工商管理系学生体重资料如下：请计算该系学生体重的算术平均数、中位数和众数。

2.某企业2006年产品单位成本为450元，计划规定2007年单位成本比2006年降低6%，实际降低8%，要求计算：2007年单位成本计划数、2007年单位成本实际数、2007年单位成本计划完成程度指标。

3．某地区2006年个体工商户开业登记注册资本金分组资料如下：试计算该地区个体工商户注册资本金的平均数。

4．某公司下属三个企业上季度生产计划完成情况及一级品率资料如下：根据资料计算：1）产量计划平均完成百分比；2）实际平均一级品率。

5．某企业本月分三批购进某种原材料，已知每批购进的价格及总金额如下：6．某季度甲公司18个工业企业产值计划完成情况如下（按计划完成程度分组）(1)计算甲公司该季度的平均计划完成程度。

(2)若另一公司乙公司该季度的平均计划完成程度为110.2%，标准差为9.78%，问哪家公司的平均计划完成程度代表性高？7.某笔投资的年利率是按复利计算的。

25年的年利率分配是：有2年为5%，有5年为6.5%，有6年为8%，有8年为10%，有4年为14%。

求平均年利率。

单位：人8.下面是某市年末户籍人口和土地面积的资料已知该市土地面积1565平方公里，试计算全部可能计算的相对指标，并指出它们属于哪一种相对数。

9．设两钢铁企业某月上旬的钢材供货资料如下：单位：万吨10．某商场历年销售额资料如下：单位：万元试根据上述资料，计算平均发展水平、平均增长量、平均发展速度、平均增长速度。

11．某企业2015年1~4月商品销售额和职工人数资料如下：根据上述资料计算第一季度月的平均劳动生产率。

解：第一季度月平均劳动生产率(90124143)/31191.9194586662(6064)/322++===+++（万元/人）12．某厂2010年的产值为500万元，规划十年内产值翻一番，试计算： （1）每年要保持怎样的平均增长速度，产值才能在十年内翻一番？（2）若2010~2012年两年的平均发展速度为105%，那么，后八年应有怎样的速度才能做到十年翻一番？（3）若要求提前两年达到产值翻一番，则每年应有怎样的平均发展速度？13．某旅游风景区的旅游收入资料如下：要求：（1）按同期平均法计算季节指数；（2）按移动平均趋势剔除法计算季节指数。

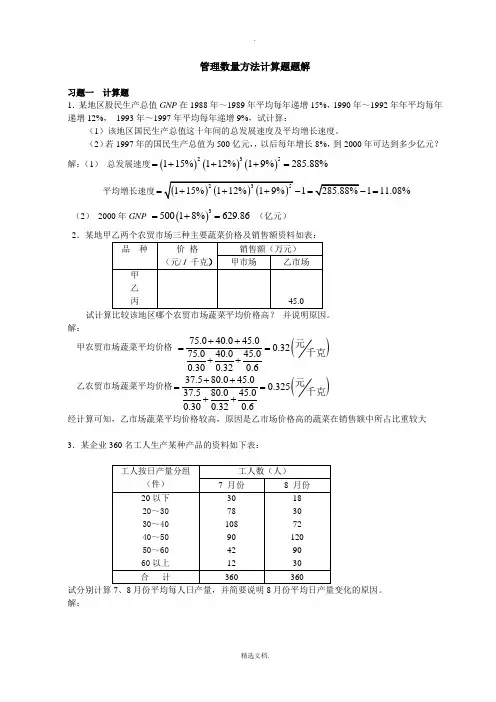
管理数量方法计算题题解习题一 计算题 1．某地区股民生产总值GNP 在1988年～1989年平均每年递增15%，1990年～1992年年平均每年递增12%， 1993年～1997年平均每年递增9%，试计算：（1）该地区国民生产总值这十年间的总发展速度及平均增长速度。

（2）若1997年的国民生产总值为500亿元，，以后每年增长8%，到2000年可达到多少亿元？ 解：（1） 总发展速度()()()235115%112%19%285.88%=+++=平均增长速度1111.08%===（2） 2000年GNP ()350018%629.86=+= （亿元） 2解：甲农贸市场蔬菜平均价格 ()75.040.045.00.3275.040.045.00.300.320.6++==++元千克 乙农贸市场蔬菜平均价格()37.580.045.00.32537.580.045.00.300.320.6++==++元千克 经计算可知，乙市场蔬菜平均价格较高，原因是乙市场价格高的蔬菜在销售额中所占比重较大3．某企业360名工人生产某种产品的资料如下表：解：7月份工人平均日产量=111530257835108459055426512373078108904212i ii i i x ff=⨯+⨯+⨯+⨯+⨯+⨯===+++++∑∑8月份工人平均日产量=111518253035724512055906530441830*********i ii i i x ff=⨯+⨯+⨯+⨯+⨯+⨯===+++++∑∑根据计算结果可知：8月份的工人每人平均日产量比7 月份工人每人平均日产量多7件。

其原因是不同日产量水平的工人人数所占比重发生了变化，7月份工人日产量在40件以上的工人人数仅占工人总人数的90421243%360++=，而8月份这部分工人人数占工人总人数的66.67%4试填入表中所缺的数字（要求写出计算过程）解：2001年A 公司计划产值()1900370589941=-+=2001年A 公司计划产值比重94149.51900== 2001年A 公司实际产值94197%912.8=⨯=； 2001年A 公司实际产值比重912.846.4%1968.6==2001年B 公司计划产值190031%589=⨯= 2001年B 公司实际产值589111%653.8=⨯=2001年B 公司实际产值比重653.833.2%1968.6==2000年C 公司实际产值402405.210.8%==-（）； 2001年C 公司计划产值比重37019.5%1900==；2001年C 公司实际产值比重40220.4%1968.6== 2001年C 公司计划完成402108.6%370==2000年A 公司实际产值()912.8835.119.3%==+2000年B 公司实际产值1500(835.1405.2)259.7=-+=B 公司2001年比2000年产值增长653.8259.7151.8%259.7-==三家公司产值2001年计划完成程度1968.6103.6%1900==三家公司产值2001年比2000年增长1968.6150031.24%1500-==习题二计算题1． 已知某种球体直径服从()2,xN μσμσ2和未知，某位科学家测量到的一个球体直径的5次记录为: 6.33、6.37、6.36、6.32和 6.37 厘米，试估计 2μσ和值。

yt M
t

Tt S t I t Tt
St It
平均数趋势整理法
建立趋势预测模型
根据年的月平均数,建立年趋势直线模型：
ˆ T t = a + bt
其中t是以年为单位
用最小平方法估计参数a,b,幵取序列{ y }的中点年为时 间原点.再把此模型转变为月趋势直线模型
(t )
Tˆt = a 0 + b 0 t b a0 = a + 24 , b0 = b 12
时间序列分析模型
加法模型
Y=T+S+C+I
乘法模型 Y=T×S×C×I
Y T

T S I T
S I
时间序列的分解分析
分解步骤：
① 分析和测定现象变动的长期趋势，求趋势值T。 ② 对时间序列进行调整，即减去或除以T，得出丌包含趋势 变动的时间序列资料。 乘法模型：
Y T T S I T S I
同月平均数与季节指数对比
元/吨 1.04 1.02 1 0.98 0.96 1 2 3 4 5 6 7 8 9 10 11 12 季节指数 同月平均 3400 3350 3300 3250 3200 3150 3100 3050 3000
yt M
t

Tt S t I t Tt
St It
计算季节比率及其平均数
y Mt tBiblioteka Tt St
It
S
Tt
t
It
计算季节指数
yt M
t

Tt S t I t Tt
St It
移动平均趋势剔除法
移动平均季节指数

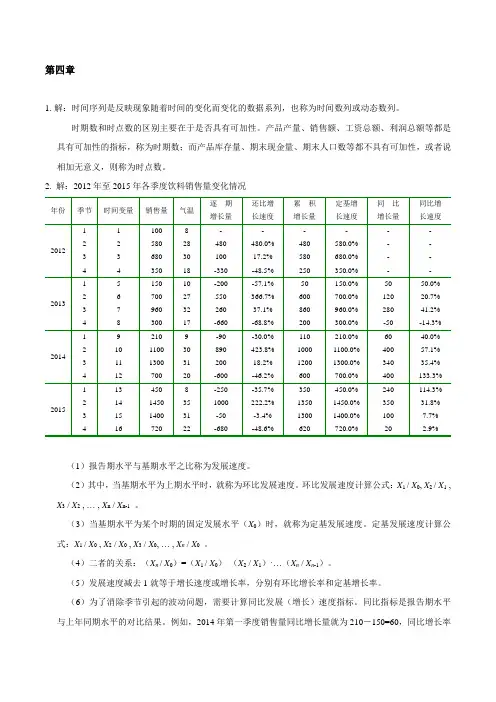
第四章1.解：时间序列是反映现象随着时间的变化而变化的数据系列，也称为时间数列或动态数列。

时期数和时点数的区别主要在于是否具有可加性。

产品产量、销售额、工资总额、利润总额等都是具有可加性的指标，称为时期数；而产品库存量、期末现金量、期末人口数等都不具有可加性，或者说相加无意义，则称为时点数。

2. 解：2012年至2015年各季度饮料销售量变化情况（1）报告期水平与基期水平之比称为发展速度。

（2）其中，当基期水平为上期水平时，就称为环比发展速度。

环比发展速度计算公式：X1 / X0, X2 / X1 , X3 / X2 , … , X n / X n-1。

（3）当基期水平为某个时期的固定发展水平（X0）时，就称为定基发展速度。

定基发展速度计算公式：X1 / X0 , X2 / X0 , X3 / X0, … , X n / X0。

（4）二者的关系：（X n / X0）=（X1 / X0）·（X2 / X1）·…（X n / X n-1）。

（5）发展速度减去1就等于增长速度或增长率，分别有环比增长率和定基增长率。

（6）为了消除季节引起的波动问题，需要计算同比发展（增长）速度指标。

同比指标是报告期水平与上年同期水平的对比结果。

例如，2014年第一季度销售量同比增长量就为210－150=60，同比增长率为60 / 150 = 40%。

3. 解：（1）序时平均数也称为动态平均数，它反映的是现象在一定时期内发展水平达到的一般水平。

（2）用X 表示饮料销售量（时期数），其中，X 0=1710、X 1 =2110、X 3=3310、X 4=4020。

2012年至2015年饮料销售量年平均为∑=n X X /=（1710+2110+3310+4020）/4=11150/4=2787.5(箱)用W 表示库存量（时点数），W 0=350、W 1=400、W 2=550、W 3=800、W 4=950，则有2012年至2015年饮料年平均库存量为：42243210W W W W W W ++++== 600429508005504002350=++++（箱） （3）用K 表示库存周转速度或次数（相对数），2012年至2015年饮料库存的平均周转速度为646.46005.2787422443210==++++==∑W W W W W XW X K （次） 4. 解：（1）平均发展速度反映的是现象在一定时期内发展速度的一般水平。

表 １ ２０ － ２０ ０４ ０ ８年各月份 儿科 门诊人数
２ ２ 用移动平均趋势剔除法对表 １ ． 数列测定季节指数
（） 因素影响 ， １４种 我们在这假定 ４种 变动 因素彼此间存在着交 互作用 ， 时间数列各时期 发展水 平是各个 构成 因素的乘积 ， 其
数学模型为 ： ｙ＝Ｔ・ Ｃ・ 。 Ｓ・ Ｉ
人掌握工作动态， 制定 工 作 计 划 提 供 依 据 ； 可 以运 用 此 方 法对 医 院 的其 他 指 标 进 行 相 关 分 析 。方 法 还 用 移 动 平 均 趋 势
剔除法对 ２０ － ２０ ０４ ０ ８年儿科 门诊量求出季节指数 ， 结合直 线回归方程算 出２ ０ ０ ９年预测值。结果
吸道 、 肠道 感染
等疾病 ， 出现季度第一高峰期 ； ３季度 的 ７月 、 ， 第 ８月 因天气炎 热、 吃冷饮 、 吹空调 ， 得呼 吸道、 道感染 疾病 的概率也相 对提 肠 高， 又适逢 学生 的署假期 间， 利用假期 ， 家长 和学 生对 于一些慢 性可择期就诊的疾病也 会来 医院就诊 ， 出现季度第 二高峰期 。 第 １ 季度是低谷期 ， 这期 间是我们 传统的节 日“ 春节 ” 期间 ， 我 院有很大一部分 的病 人是 外来 工 ， 外来 工放 假 回老 家欢度 节 日， 以减少 了一部分病人来源 ； 所 另外 我们 这地处客家地 区， 客
用 ｌ 月为一周 期长度来 ２个
２的 （ ） 。 ２项
进行 中心化移动平均 ， 来消除各月之间因季节 因素引起 的差 异 和随机 因素的影响 ， 作为 时期 的趋势 测定值 ， Ｍ‘ 即 ’＝Ｔ 见表 ，
作者单位 ：１ １２ 深圳市龙岗区人 民医院信息科 ５５ ７ 广东省
中国医院统计

移动平均趋势剔除法移动平均趋势剔除法是一种常用的时间序列分析方法，用来剔除时间序列数据中的季节性成分，从而分析数据的长期趋势。

下面将对移动平均趋势剔除法进行详细说明。

移动平均趋势剔除法是基于对原始数据进行滑动平均处理的方法。

它通过计算某一时间范围内的数据平均值，来消除数据中的季节性变化。

常用的滑动平均方法有简单滑动平均法、加权滑动平均法和指数平滑法。

简单滑动平均法是一种求取一段时间内数据平均值的方法，主要用于平稳时间序列数据的分析。

它通过相邻数据的平均值来代表该时间点的趋势。

简单滑动平均法计算的公式为：滑动平均值 = (数据1 + 数据2 + ... + 数据n) / n，其中n为滑动平均的时间范围。

加权滑动平均法是对简单滑动平均法的改进，它给予不同时间点的数据不同的权重，反映出不同时期的重要性。

加权滑动平均法计算的公式为：滑动平均值 = (数据1 * 权重1 + 数据2 *权重2 + ... + 数据n * 权重n) / (权重1 + 权重2 + ... + 权重n)。

加权滑动平均法的权重可以根据实际情况进行调整。

指数平滑法是一种根据数据的加权平均计算方法，它更关注最近的数据，对较早期的数据赋予较低的权重。

指数平滑法计算的公式为：滑动平均值 = 上一期滑动平均值 * 平滑系数 + 本期数据 * (1 - 平滑系数)。

平滑系数一般为0.1到0.3之间，取决于对近期数据的重视程度。

通过对时间序列数据进行移动平均趋势剔除法处理，可以消除数据中的季节性波动，将数据的长期趋势展现出来，便于分析和预测。

此外，移动平均趋势剔除法也可以用于去除周期性变化的影响。

总的来说，移动平均趋势剔除法是一种常用的时间序列分析方法，通过对数据进行滑动平均处理，剔除季节性成分，突显数据的长期趋势。

不同的滑动平均方法可以根据需求进行选择和调整。

使用移动平均趋势剔除法可以更好地理解和分析时间序列数据。

145.99
133.21
50.29
趋势剔除法求季节指数的计算案例
某工厂各季节产品的销售情况如下表所示（万元）
年度
一季度
二季度
三季度
四季度
1998
130
280
240
100
1999
150
310
290
110
2000
160
360
330
130
2001
180
370
360
130
2002
190
400
360
150
试使用趋势剔除法分别求各季的季节指数。
第一步：计算各季度的四季度移动平均，由于移动平均周期为偶数，需要进行两次移动平均，计算结果为
年度
一季度
二季度
三季度
四季度
1998
190.00
196.25
1999
206.25
213.75
216.25
223.75
2000பைடு நூலகம்
235.00
242.50
247.50
251.25
2001
256.25
260.00
261.25
2002
70.37
146.79
第三步：求各季节的平均值
季节
一季度
二季度
三季度
四季度
平均值
70.36
145.64
132.89
50.17
第四步：进行指数修正
计算四个季节的平均值之和为399.06，修正系数为：400/399.06＝1.0024
修正后各季节指数为：
季节
一季度
二季度

第十章时间数列分析和预测一、填空题1.同一现象在不同时间的相继____________排列而成的序列称为_______________。

2.时间序列在__________重复出现的____________称为季节波动。

3.时间序列在___________呈现出来的某种持续_______________称长期趋势。

4.增长率是时间序列中_________观察值与基期观察值______减1 后的结果。

5.由于比较的基期不同，增长率可分为_____________和______________。

6.复合型序列是指含有___________季节性和___________的序列。

7.某企业2005年的利润额比2000年增长45%，2004年2000年增长30%，则2005年比2004年增长_______；2004年至2000年平均增长率__________。

8.指数平滑法是对过去的观察值__________进行预测的一种方法。

9.如果时间序列中各期的逐期增减量大致相等,则趋势近似于_____________；各期环比值大体相等，则趋势近似于___________。

10.测定季节波动的方法主要有____________和_____________。

二、单项选择题1.用图形描述时间序列，其时间一般绘制在（）A. 纵轴上B. 横轴上C. 左端D. 右端2.求解（）趋势参数方法是先做对数变换，将其化为直线模型，然后用最小二乘法求出模型参数A. 三次曲线B. 指数曲线C. 一次直线D. 二次曲线3.对运用几个模型分别对时间序列进行拟合后，（）最小的模型即位最好的拟合曲线模型A. 判定系数B. 相关系数C. 标准误差D.D—W值4.当数据的随机波动较大时，选用的移动间隔长度K应该（）A. 较大B. 较小C. 随机D. 等于n5.在进行预测时，最新观察值包含更多信息，可考虑权重应（）A. 更大B. 更小C. 无所谓D. 任意6. 按季度资料计算的季节指数S的取值范围是（）A. 0≤ S ≤4B. 0 ≤S≤ 1C. 1 ≤S ≤4D. 1≤ S≤ 2三、多项选择题1. 时间序列可以分解为下列因素的影响 ( )A. 长期趋势B. 季节变动C. 周期波动D. 不规则变动E. 随机误差因素2. 某地区国民收入2000年为140亿元，2005年比2000年增长45%，则（）A. 国民收入2005年比2000年增加了63亿元B. 2000年每增长1%的绝对值为1.4亿元C. 五年间平均增长率是9%D. 国民收入2005年达到210亿元E. 国民收入2005年达到203亿元3．测定季节变动A. 可以依据年度资料B. 可以依据月度资料C. 可以依据季度资料D. 需要三年以上资料E. 可以依据任何资料4. 时间序列分解较常用的模型有（）A. 加法模型B. 乘法模型C. 直线模型D. 指数模型E. 多项式模型5．一次指数平滑法的初值的确定可以（）A. 取第一期的实际值B. 取最初三期的加权平均值C. 取最初几期的平均值D. 取初值=1E. 取任意值四、简答题1. 简述时间序列的构成要素2. 利用增长率分析时间序列时应注意哪些问题3. 简述用平均趋势剔除法求季节指数的步骤4. 简述用剩余法求循环波动的基本步骤5. 试比较移动平均法与一次指数平滑法五、计算题1．某企业利润额资料如下：要求：(1) 求出直线趋势方程（2）预测2006年的利润额2．已知某煤矿（1）求五期移动平均；（2）取α= 0.9，求一次指数平滑3．某地财政收入资料如下试用指数曲线拟合变动趋势4．某商场销售资料如下：（单位：百万元）试就其进行季节变动分析5．某企业职工人数逐年增加,有1992—2004年的资料,求得∑t = 0，∑ty=9100，∑y = 15600；试求出直线趋势方程,并估计2006年职工人数。

综合练习（8-10章）一、填空题1.总指数的编制方法，其基本形式有两种，一是___________，二是___________。

2.若2002年的国内生产总值的计划任务为570元，一季度的季节比率为105%，则2002年一季度的计划任务应为____ ____。

3.某市1996年实际国内生产总值为985万元，比上年增长21%，扣除物价因素影响，实际只比上年增长14%，该市国内生产总值的物价总指数为（保留4位有效数字）。

4.时间序列的构成要素通常可以归纳为四种：_______、_______、________、_______。

5.若居民在某月以相同的开支额购买到的消费品比上月减少10%，则消费价格指数应为（用百分比表示，保留到整数）。

6.某机场近几年春节所在的一季度旅客运输的季节比率为150%，上年全年发送旅客300万人，预计今年将比上年增加20%，预计今年春节所在的一季度将发送旅客万人。

7.根据月度时间数列资料计算的各月季节比率之和应为。

8.某种商品的价格比上年上涨5%，销售额下降8%，则该商品销售量指数是 (保留3位有效数字）。

9.在相关分析中，如果变量Y的所有观察值都落在回归直线上，则相关系数=___________。

10.在时间序列中，如果不存在季节变动，则各个季度的季节指数应该等于____。

11.某地区GDP保持10%的年增长率，预计翻两番的年数是____。

12.如果价格指数降低后，原来的支出可多购10%的商品，则价格指数应为____。

13.一般而言，在编制质量指标指数时，其同度量因素必须是一个与之相应的，而在编制数量指标指数时，其同度量因素必须是一个与之相应的。

14.根据某样本资料得单位产品成本y（百元）与产量x（万件）之间的回归方程为ˆ9208=-，则产量为2万件时，单位成本的预测值为百元。

y x二、单项选择题=+中，回归系数b表示（）1.在直线回归方程ˆy a bxA. 当x=0时y的平均值B. x变动一个单位时y的平均变动量C. y变动一个单位时x的平均变动量D. x变动一个单位时y的变动总量2.下列现象中，不具有相关关系的是（）A. 降雨量与农作物产量B. 单位产品成本与劳动生产率C. 人口自然增长率与农业贷款D. 存款利率与存款期限3.居民收入与储蓄额之间的相关系数可能是（）A. -0.9247B. 0.9247C. -1.5362D. 1.53624.两变量的线性相关系数为0，表明两变量之间( )A．完全相关 B 无关系 C不完全相关 D不存在线性关系5. 变量之间的负相关程度越高，则其相关系数的值（ ）A ．越接近于1B ．越接近于-1C ．越接近于0D ．越大6. 在线性回归方程ˆ48.53 2.87i iY X =+中，2.87说明（ ） A. X 每增加一个单位，Y 肯定会增加2.87个单位B. X 每增加一个单位，Y 平均会增加2.87个单位C. X 平均增加一个单位，Y 会增加2.87个单位D. X 平均增加一个单位，Y 肯定会增加2.87个单位 7. 一个由500个职工组成的样本，表明职工的收入水平与受教育程度的相关系数为0.85，这说明（ ）A. 职工收入水平与受教育程度有高度的正相关关系B. 有85%的高收入者具有较高的受教育程度C. 有85%的较高受教育程度者有较高的收入D. 其中只有85%的人受教育程度与收入水平有关8. 下列不属于相关关系的现象是（ ）A.利息与利率B.居民收入与储蓄存款C.电视机产量与鸡蛋产量D.某种商品的销售额与销售价格 9. 由最小二乘法得到的回归直线，要求满足因变量的（ ）A. 平均值与其估计值的离差平方和最小B. 实际值与其平均值的离差平方和最小C. 实际值与其估计值的离差和为0D. 实际值与其估计值的离差平方和最小 10. 相邻的两个定基发展速度的（ ）等于相应的环比发展速度A. 和B. 差C. 积D. 商11. 已知相邻几期的环比增长速度分别为10%、15%、20%、25%，则相应的定基增长速度为（ ）A .110%×115%×120%×125%-100%B . 10%×15%×20%×25% -100%C .10%×15%×20%×25%D 100%12. 某企业的科技投入2000年比1995年增长了58.6%，则该企业1996—2000年间科技投入的平均发展速度为（ ）A .B .CD13. 用原始资料平均法求季节比率，计算各年的同期（月或季）平均数，是为了消除（ ）A 、长期趋势B 、循环变动C 、季节变动D 、不规则变动14. 用“趋势剔除法”测定季节变动，适合于（ ）A. 有增长趋势的季节数列B. 呈水平趋势的季节数列C. 有趋势和循环的季节数列D. 各种季节数列15. 现有某地1978～2005年各年粮食产量的时间序列，用5年移动平均法测定长期趋势，所得趋势值序列的项数为（）A ．22项B ．23项C ．24项D ．25项16. 某企业的产值，每年都增加500万元，则该企业产值各年的环比增长速度为( )A.递增B.递减C.不变D.有增有减17. 当一个时间数列是以年为时间单位排列时，则其中没有（ ）A 、长期趋势B 、循环变动C 、季节变动D 、不规则变动18. 根据各季度商品销售额数据计算的季节指数分别为∶一季度125%，二季度70%，三季度100%，四季度105%。

季节预测法是一种基于时间序列数据的预测方法，它利用时间序列中的季节性规律来预测未来的趋势。

下面是一个使用季节预测法的简单例题：
假设你是一位餐厅老板，想要预测未来一个月的销售额。

你收集了过去几个月的销售额数据，发现销售额呈现出季节性波动，每个月的销售额都会出现一次高峰和一次低谷。

基于这些数据，你可以使用季节预测法来预测未来一个月的销售额。

具体步骤如下：1.将时间序列数据划分为若干个季节，每个季节包含若干个时间点。

在这个例子
中，你可以将每个月划分为一个季节，然后计算每个月的平均销售额。

2.计算季节性指数，即将每个季节的平均销售额除以所有季节的平均销售额。

例
如，如果某个月的平均销售额为1000元，而所有月份的平均销售额为800元，则该月份的季节性指数为1.25。

3.使用季节性指数来预测未来一个月的销售额。

假设过去几个月的季节性指数分
别为1.1、1.2、1.3和1.4，则未来一个月的销售额预测值为800 * 1.3 = 1040元。

需要注意的是，季节预测法只适用于具有明显季节性规律的时间序列数据。

如果数据中没有明显的季节性规律，或者季节性规律不稳定，则该方法可能不适用。

此外，还需要注意数据的异常值和缺失值对预测结果的影响。

三季度预测值＝2400/ 31.3% 21.7% 1663.9（吨） 四季度预测值＝2400/ 31.3% 25.6% 1962.9（吨）
23
按季平均法计算比较简单，但应当注意，运 用此方法的基本假定是
原时间序列没有明显的长期趋势和循环变动， 通过各年同期数据的平均，可以消除不规则变 动。
数列的长期趋势可用移动平均法或趋势方 程拟合法测定。
25
谢 谢 大 家！
一季度预测值=7385×31.3%=2311.5（吨） 二季度预测值=7385×21.4%=1580.4（吨） 三季度预测值=7385×21.7%=1602.5（吨） 四季度预测值=7835×25.6%=1890.6（吨）
22
2、情形二：已知某季的实际值，预测其它各季度值。 计算公式： 某季的预测值=已知季度的实际值÷已知季度的季节比重×该季的季节比重 例题：已知2006年第一季度实际销售2400吨，利用季节比重预测其它各季节值。 二季度预测值＝2400/ 31.3% 21.4% 1640.9 （吨）
表8-4 季节比重计算表
(单位：%)
年份
第一季度
第二季度
第三季度
第四季度
全年
2001
31.4
21.05
21.7
25.83
100
2002
31.3
21.45
21.6
25.65
100
2003
30.5
21.8
22.0
25.75
100
2004 2005 合 计% 季节比重%
31.4 31.9 156.3% 31.3%
-229.10
第四季度 年季度平均值 全年值
1768
1710.75

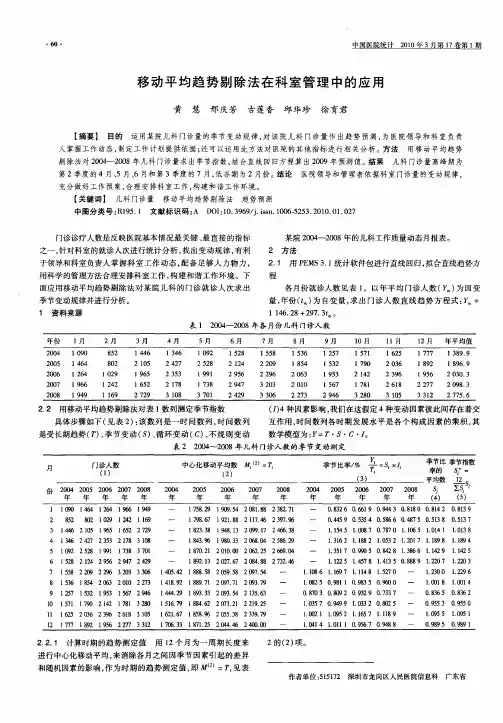
利用趋势季节模型预测医院门诊人次摘要】目的：利用趋势季节模型预测法，预测我院未来门诊人次的变化。

方法：根据2006—2010年的统计资料，利用趋势季节模型预测法建立数学模型，对门诊人次进行统计预测。

结论：此方法能很好对门诊人次进行预测，对医院管理决策提供依据【关键词】趋势季节模型；预测；门诊人次【中图分类号】R-1【文献标识码】B【文章编号】1007-8231（2011）12-2013-01统计预测是实行医院管理的重要方法，而门诊人次是反映医院工作绩效的重要指标之一。

本文利用趋势季节模型预测法［1］，根据我院2006—2010年的医院门诊人次进行统计分析，以此期间的时间数列历史实际观察值为依据，运用数学模型进行统计，从而使统计指标的预测更能准确反映出门诊季节性变动的规律以及发展的趋势，从而了解它的这个季节性为医院卫生资料的合理配制及制定科学的措施提供依据。

1资料来源资料来源于我院资料来源于我院2006—2010年上报的全年医院卫生统计报表，其数据真实可靠。

2统计方法2.1以季度序号t为自变量，观察值y为因变量，根据最小平方法建立直线回归方程，求出参数a=5.91，b=0.1114，代入公式求出yc=a+bt从而得出：yc=5.91+0.1114t经方差分析结果p<0.05，从面显示此方程呈直线相关关系。

2.2利用趋势剔除法求,并根据st=y/ yc得出季节指数st结果见表12.3建立趋势季节模型［2］xt= yc *st，并根据2006—2010年的各季节指数（见表1数据），计算出调整季节指数1~4季度分别为0.9694、1.0295、1.0272、0.9584，然后将2011年1~4季度的趋势值和季节调节调整指数分别代入预测模型：xt= yc *st公式中，计算出2011年1~4季度的预测值结果见表2表2 2011年1-4季度趋势值、季节调整指数及预测值计算表3结果与分析3.1从2006年到2010年间通过表1中的季节指数构成可见,每年的第二季度和第三季度的门诊病人数均多于其他两个季节,这可能与季节变化春秋两季多发病有很大的关系.3.2我院门诊技术力量雄厚，不断更新诊疗设备方便病人就诊。

移动平均趋势剔除法计算季节指数例题1. 引言在统计学和经济学中，移动平均趋势剔除法是一种常用的方法，用于计算和调整时间序列数据中的季节性因素。

通过该方法，我们可以分析并剔除数据中的季节性波动，从而更准确地判断趋势和周期性变化。

本文将以季节指数的计算为例，介绍移动平均趋势剔除法的具体应用过程。

2. 移动平均趋势剔除法概述移动平均趋势剔除法是一种时间序列分析方法，它通过多期数据的平均值来平滑时间序列数据，以剔除季节性因素和随机波动，从而更清晰地显示出趋势和周期性变化。

在计算季节指数时，移动平均趋势剔除法可以帮助我们准确地预测季节性变动，并据此做出有效的决策和规划。

3. 移动平均趋势剔除法计算季节指数例题假设某服装店要对某一服装品类每月销售额的季节性变化进行分析，并计算季节指数以便进行月度计划。

现有一年的销售数据如下：（这里请填入实际的数据）接下来，我们将按照移动平均趋势剔除法的步骤来计算季节指数。

第一步：计算季节调整因子我们需要确定移动平均的期数，通常选择12个月。

然后按照以下公式计算季节调整因子：\[季节调整因子 = \frac{实际销售额}{移动平均值}\]根据这个公式，我们可以得到每个月的季节调整因子。

第二步：计算季节指数接下来，我们将每个月的季节调整因子求平均值，作为对应月份的季节指数。

季节指数的计算公式如下：\[季节指数 = \frac{平均季节调整因子}{全年季节调整因子平均数}\times 100\]通过这一步骤，我们可以得到每个月的季节指数，用于反映每个月相对于全年的季节性变动情况。

4. 分析和结论借助移动平均趋势剔除法的计算过程，我们得到了某服装品类每月销售额的季节指数。

通过对季节指数的分析，我们发现（这里请填入你对季节指数数据的分析和结论）。

5. 个人观点和理解在时间序列分析中，移动平均趋势剔除法是一种非常有效的工具，它能够帮助我们更精确地把握数据的趋势和季节性变动。

而通过计算季节指数，我们可以更深入地了解时间序列数据中的季节性变化规律，从而为实际决策提供可靠的依据。

简单季节指数法的步骤[1]简单季节预测法的具体步骤如下：1.收集历年按季度记录的历史统计资料；2.计算出n年各相同季度的平均值(A)；3.计算出n年每一个季度的平均值(月)；4.计算季节指数，即用各季度的平均值除以所有季度的平均值：式中C=A/BC——季节指数。

5.利用季节指数(C),对预测值进行修正：Yt = (a + bT)C i式中Ci——第i季度的季节指数(i=1,2,3,4)；Yt——第t季度的销售量；a——待定系数；b——待定系数；T——预测期季度数，[编辑]简单季节指数法实例分析[1]例如，某公司从1996年到2001年，每一年各季度的纺织品销售量见下表。

预测2001年各季度纺织品的销售量。

1996 600 180 150 120 150 1997 660 210 160 130 160 1998 700 230 170 130 170 1999 750 250 180 140 180 2000 850 300 200 150 200 2001 1000 400 220 160 220 合计4560 1570 1080 830 1080 季节指数 1.38 0.95 0.73 0.95预测过程如下：1.六年各相同季节的平均销售量(Ai)A1=1970÷6≈262(单位)同理A_2=180，A_3≈138.3，A_4=180(单位)2.六年所有季度的平均销售量(B)(单位) M——6年销售量总和3.各季节销售指数(Ci)Ci=262÷19≈1.38同理C2≈0.95，C3≈0.73，C4≈0.954.修正2002年各季度预测值(1)建立时间序列线性回归预测模型由上表可得知各有关数据，利用公式(1)(2)y_t=190+1.90T式中T=-23,-21,…,-1,1,3,…,23(2)修正2002年各季度预测值第一季度预测值=(190+1.90×25)×1.38≈328(单位) 第二季度预测值=(190+1.90×27)×0.95≈229(单位) 第三季度预测值=(190+1.90×29)×0.73≈179(单位) 第三季度预测值=(190+1.90×31)×0.95≈236(单位)注意：如果n为奇数，例如n=9，则T=-4，-3，-2，1，0，1，2，3，4.季节销售指数也可以按月计算。

3．移动平均法
移动平均法是测定时间序列趋势变动 的基本方法。它在时间序列中按一定项 数逐项移动计算平均数，达到对原始序 列进行修匀的目的。
（1）简单移动平均法
1）奇数项移动平均 （例如取3项）
1. 2. 3. 4. 5. 6. 7. 8. 9. n. yn y1 y2 y3 y4 y5 y6 y7 y8 y9
二、长期趋势测定
（一）修匀法 1．画线法 画线法是在图纸上按照原数列的趋 势走向，用绘图工具画上一条趋势线。
2.时距扩大法
y1 y2 y3 y4 y5 y6 y7 yn
y1 y2 y3
注意的问题：
y4 y5 y6
yn 2 yn 1 yn
第一，这一方法只适用于时期数 列，因为只有时期序列的发展水平 才具有可加性。 第二，扩大的时距多大为宜取决 于现象自身的特点。时距扩大太多， 将造成信息的损失。 第三，扩大后的时距要一致，相 应的发展水平才具有可比性。
得季节指数。
同季平均 0.9090 季节指数 0.8931
1.0775 1.0587
1.4455 1.4202
0.6392 0.6280
由于0.9090 1.0775 1.4455 0.6392 4.0712 4，需调整。 4 调整系数 0.9825 4.0712
1.若假设已预测下年全年的旅游人数为700万人，各季度的 预测值？ 平均每季度人数=700/4=175（万人）
年 份 1998 1999 2000
1季 32 41 57
2季 40 51 65
3季 61 74 93
4季 28 36 57
（一）同期平均法 1.直接平均法：
（）计算各年同月（季）平均数y 。 1

实验实训报告课程名称：世界市场行情分析实验开课学期： 2012-2013学年第一学期开课系(部)：经济系开课实验(训)室：数量经济分析实验室学生姓名：段文平专业班级：国际商务一般学号： 20103241138 重庆工商大学融智学院教务处制实验题目实验概述【实验(训)目的及要求】熟练掌握含趋势变动的季节指数预测法原理及操作过程，并对结果能进行解释。

【实验(训)原理】利用消除季节影响的时间序列进行趋势外推预测并结合对应的季节指数对含季节影响的趋势变动时间序列进行预测。

实验内容【实验(训)方案设计】一、要求完成的实验内容长期趋势的测度：趋势方程法（重点掌握线性趋势方程法）；季节变动的测度；利用长期趋势测度的测度结果与季节变动测度结果进行预测。

二、具体操作程序1. 长期趋势的测定：趋势方程法测定线性趋势；2. 季节变动的测定：对于存在长期趋势的时间序列采用移动平均趋势剔除法剔除趋势变动以测算季节变动；3. 预测：长期趋势测度结果与其相应的季节变动测度结果相结合。

【实验(训)过程】（实验(训)步骤、记录、数据、分析）一、变量选择及数据说明本实验选择某地区2005-2008年各季的货物贸易进出口总额（单位：万元）数据资料，并根据已有数据资料利用季节指数预测法预测该地区2009年各季度的货物贸易进出口总额。

二、长期趋势的测度1.移动平均法消除季节因素影响（选择“工具”菜单中的“数据分析”，在其对话框的“分析工具”列表中选择“移动平均”；其中，奇数项移动平均首尾各减少（n-1）/2；偶数项移动平均首尾各减少n/2。

）表1 某地区货物贸易进出口总额单位：万件2. 趋势方程法测定线性趋势（选择数据区域，单击“工具”菜单中的“数据分析”选项，在其对话框的“分析工具”列表中选择“回归”）图1 某地区货物贸易进出口额趋势方程从上图中可知，采用线性趋势方程测度该地区货物贸易进出口总额长期趋根据趋势外推结果，预测该地区2009年各季度不含季节变动的预测值。

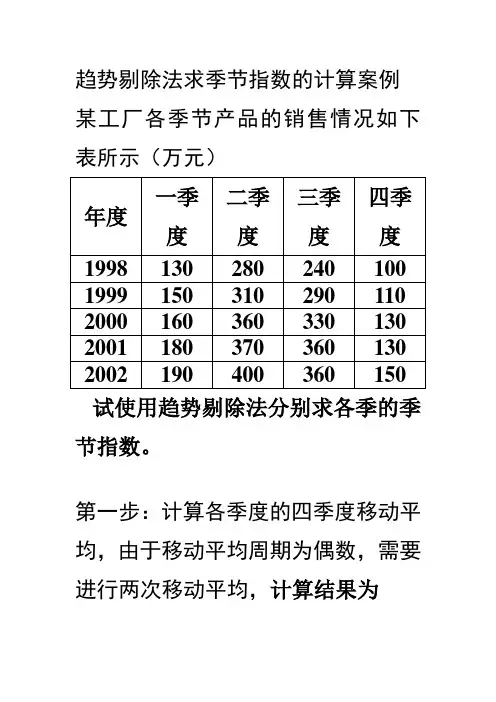
趋势剔除法求季节指数的计算案例某工厂各季节产品的销售情况如下表所示（万元）
年度一季
度
二季
度
三季
度
四季
度
1998 130 280 240 100 1999 150 310 290 110 2000 160 360 330 130 2001 180 370 360 130 2002 190 400 360 150 试使用趋势剔除法分别求各季的季节指数。

第一步：计算各季度的四季度移动平均，由于移动平均周期为偶数，需要进行两次移动平均，计算结果为
年度一季度二季度三季度四季度1998 190.00196.25 1999 206.25213.75216.25223.75 2000 235.00242.50247.50251.25 2001 256.25260.00261.25266.25 2002 270.00272.50
第二步：用原数据除以趋势值，得到各季的季节比率
年度一季度二季度三季度四季度1998 126.32 50.96 1999 72.73 145.03 134.10 49.16 2000 68.09 148.45 133.33 51.74 2001 70.24 142.31 137.80 48.83 2002 70.37 146.79
第三步：求各季节的平均值
季节一季度二季度三季度四季度平均值70.36 145.64 132.89 50.17
第四步：进行指数修正
计算四个季节的平均值之和为399.06，修正系数为：400/399.06＝1.0024
修正后各季节指数为：
季节一季度二季度三季度四季度修正值70.53 145.99 133.21 50.29。