两回转体表面的交线—相贯线
- 格式:ppt
- 大小:1.34 MB
- 文档页数:23





两共轴回转体表面相贯线的形状为相贯线是指两共轴回转体表面相互相交时形成的线段或曲线。
两共轴回转体表面相贯线的形状不仅与共轴回转体的几何形状有关,还与它们的位置、朝向以及相对运动方式等因素密切相关。
下面将从几何形状、位置与朝向、相对运动方式三个方面来探讨两共轴回转体表面相贯线的形状。
首先,两共轴回转体的几何形状对相贯线的形状有很大影响。
最简单的情况是两个圆柱体或圆锥体相贯。
当两个圆柱体或圆锥体的轴线相交于一点时,相贯线为一条射线。
当两个圆柱体或圆锥体的轴线平行时,相贯线为一条直线。
如果两个圆柱体或圆锥体的轴线相交于非垂直的点,相贯线为一条螺旋线。
此外,当一个圆柱体与一个球体相贯时,相贯线的形状为一条环线。
当两个球体相贯时,相贯线为一个球面。
其次,两共轴回转体的位置与朝向也对相贯线的形状产生影响。
当两个共轴回转体平行且轴线有一定的偏移时,相贯线为两个直线段,且与共轴回转体的轴线平行。
当两个共轴回转体有一定的夹角时,相贯线为一条曲线,其形状取决于夹角的大小和角的种类(如锥角、锐角或直角等)。
最后,两共轴回转体的相对运动方式也会影响相贯线的形状。
当两个共轴回转体以相同的转速和方向旋转时,相贯线为一条直线。
当两个共轴回转体以相同的转速但以相反的方向旋转时,相贯线为一条曲线,其形状取决于旋转速度的大小和方向。
如果两个共轴回转体以不同的转速旋转,相贯线的形状将会更加复杂,可能会出现多条线段或曲线。
综上所述,两共轴回转体表面相贯线的形状与共轴回转体的几何形状、位置与朝向以及相对运动方式密切相关。
通过对这些因素的分析,我们可以推测出相贯线的大致形状。
但是由于相贯线的形状高度复杂,没有明确的统一公式或规律可以描述,因此对于具体形状的相贯线的确定需要借助数学和计算机模拟等工具的支持。
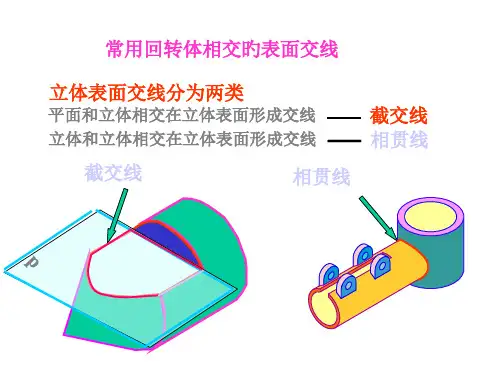


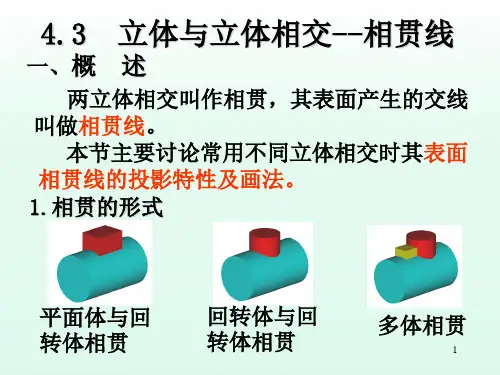

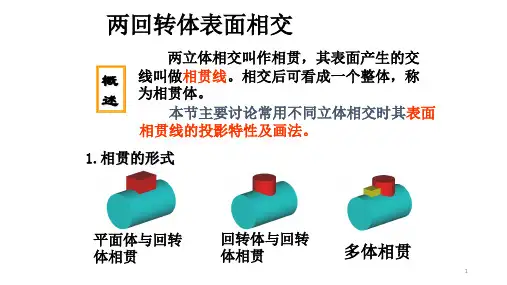
两共轴回转体表面相贯线的形状1. 引言两共轴回转体是一种几何形体,它由两个共轴旋转而成。
在制造和设计领域中,了解两共轴回转体表面相贯线的形状对于完成复杂的加工任务非常重要。
本文将详细介绍两共轴回转体表面相贯线的形状及其相关概念。
2. 什么是两共轴回转体?两共轴回转体是由两个平行且共享同一旋转轴的曲面组成。
这种几何形体常常出现在机械工程、航空航天以及汽车工业中。
3. 相贯线的定义在几何学中,相贯线指的是由两个曲面交汇而产生的曲线。
对于两个共轴回转体来说,它们的表面相贯线就是它们相交所形成的曲线。
4. 两共轴回转体表面相贯线的性质4.1 曲率半径变化根据曲率半径变化的情况,我们可以将两共轴回转体表面相贯线分为以下几类:•当曲率半径变化连续而且对称时,相贯线为圆弧。
•当曲率半径变化不连续或者不对称时,相贯线为非圆弧。
4.2 相贯线的形状两共轴回转体表面相贯线的形状取决于两个回转体的轮廓曲线。
以下是几种常见的相贯线形状:•椭圆形:当两个回转体的轮廓曲线为椭圆时,相贯线呈现出椭圆形状。
•双曲线形:当一个回转体的轮廓曲线为双曲线,另一个回转体的轮廓曲线为椭圆时,相贯线呈现出双曲线形状。
•直角螺旋形:当一个回转体的轮廓曲线为直角螺旋,另一个回转体的轮廓曲线为椭圆时,相贯线呈现出直角螺旋形状。
5. 相贯线的计算方法计算两共轴回转体表面相贯线的形状需要使用数学方法和计算机模拟。
以下是常用的计算方法:5.1 参数方程法参数方程法是一种常用于描述曲线的方法,它通过引入参数来表示曲线上的点。
对于两共轴回转体表面相贯线的计算,可以使用参数方程法来描述曲线的形状。
5.2 数值模拟法数值模拟法是使用计算机进行模拟和计算的方法。
通过将两共轴回转体的轮廓曲线输入计算机程序,可以得到相贯线的形状。
6. 应用领域了解两共轴回转体表面相贯线的形状对于以下领域非常重要:•制造工艺:在机械制造过程中,了解相贯线的形状可以帮助工程师选择合适的加工工艺和设备。