二次函数中确定特殊三角形

1 抛物线与直线形（1）
知识点归纳
抛物线与直线形的结合表现形式之一是，以抛物线为载体，探讨是否存在一些点，使其能够成某些特殊三角形，有以下常见的基本形式：
（1） 抛物线上的点能否构成等腰三角形；
（2） 抛物线上的点能否构成直角三角形；
（3） 抛物线上的点能否构成相似三角形；
解这类问题的基本思路：假设存在，数形结合，分类归纳，逐一考察。

经典例题
【例1】如图，抛物线452
+-=ax ax y 经过ABC ∆的三个顶点，已知BC ∥x 轴，点A 在x 轴上，点C 在y 轴上，且BC AC =．
（1）求抛物线的对称轴；
（2）写出C B A ,,三点的坐标并求抛物线的解析式；
（3）探究：若点P 是抛物线对称轴上且在x 轴下方的动点，是否存在PAB ∆是等腰三角形？若存在，求出所有符合条件的点P 坐标；不存在，请说明理由．
（龙岩市中考题）
思路点拨 对于（3）只需求出P 点纵坐标，将问题转化为相关线段长。

解题的关键是分情况讨论并正确画图。

【例2】已知抛物线k kx kx y 322
-+=，交x 轴于B A ,两点（A 在B 的左边），交y 轴于。

中考数学二次函数问题中三角形面积最值问题解题策略考点分析：二次函数与三角形的综合解答题一般涉及到这样几个方面：1.三角形面积最值问题2.特殊三角形的存在问题包括等腰等边和直角三角形。

这类题目一般出现在压轴题最后两道上，对知识的综合运用要求比较高。

解决此类题目的基本步骤与思路:1.抓住目标三角形，根据动点设点坐标2.根据所设未知数去表示三角形的底和高，一般常用割补法去求解三角形的面积从而得出面积的关系式3. 根据二次函数性质求出最大值.4.特殊三角形问题首先要画出三角形的大概形状，分类讨论的去研究。

例如等腰三角形要弄清楚以哪两条边为要，直角三角形需要搞清楚哪个角作为直角都需要我们去分类讨论。

注意事项：1.简单的直角三角形可以直接利用底乘高进行面积的表示2.复杂的利用“补”的方法构造矩形或者大三角形，整体减去部分的思想.3.利用“割”的方法时，一般选用横割或者竖割，也就是做坐标轴的垂线。

4.利用点坐标表示线段长度时注意要用大的减去小的。

5.围绕不同的直角进行分类讨论，注意检验答案是否符合要求。

6.在勾股定理计算复杂的情况下，灵活的构造K字形相似去处理。

原题：在（1）中的抛物线上的第二象限是否存在一点P，使△PBC的面积最大？若存在，求出P点的坐标及△PBC的面积最大值，若没有，请说明理由。

考试题型，大多类似于此。

求面积最大值的动点坐标，并求出面积最大值。

一般解题思路和步骤是，设动点P的坐标，然后用代数式表达各线段的长。

通过公式计算，得出二次函数顶点式，则坐标和最值，即出。

解法一：补形，割形法。

方法要点是，把所求图像的面积适当的割补，转化成有利于面积表达的常规几何图形。

请看解题步骤。

解法二：铅锤定理，面积=铅锤高度×水平宽度÷2。

这是三角形面积表达方法的一种非常重要的定理。

铅锤定理，在教材上没有，但是大多数数学老师都会作为重点，在课堂上讲解。

因为，铅锤定理，在很多地方都用的到。

这里，也有铅锤定理的简单推导，建议大家认真体会。

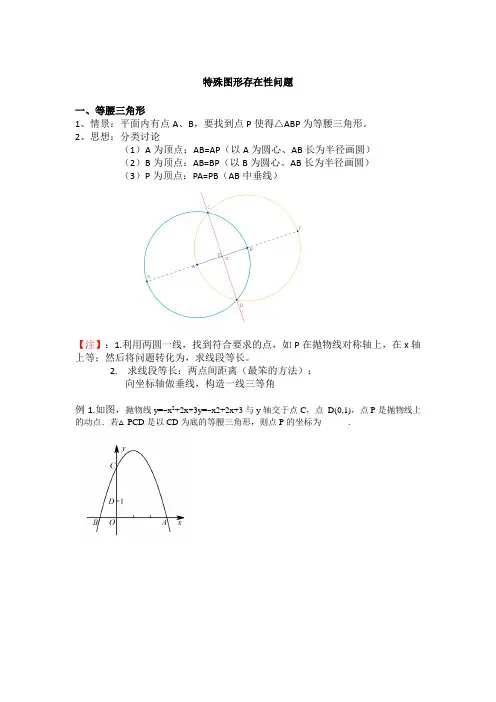
特殊图形存在性问题一、等腰三角形1、情景：平面内有点A、B，要找到点P使得△ABP为等腰三角形。

2、思想：分类讨论（1）A为顶点：AB=AP（以A为圆心、AB长为半径画圆）（2）B为顶点：AB=BP（以B为圆心、AB长为半径画圆）（3）P为顶点：PA=PB（AB中垂线）【注】：1.利用两圆一线，找到符合要求的点，如P在抛物线对称轴上，在x轴上等；然后将问题转化为，求线段等长。

2.求线段等长：两点间距离（最笨的方法）；向坐标轴做垂线，构造一线三等角例1.如图，抛物线y=−x2+2x+3y=−x2+2x+3与y轴交于点C，点D(0,1)，点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为______．练习1.如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A,B 两点，A点在原点的左侧，B点的坐标为(3,0)，与y轴交于C(0,−3)点，点P是直线BC下方的抛物线上一动点．(1)求这个二次函数的表达式；(2)在直线BC找一点Q，使得△QOC为等腰三角形，写出Q点坐标．练习2、已知抛物线y=ax2+bx+c经过A（﹣1，0）、B（3，0）、C（0，3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．练习3.如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO，直线y=﹣x+1与y轴交于点D．（1）求抛物线的解析式；（2）证明：△DBO∽△EBC；（3）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请直接写出符合条件的P点坐标，若不存在，请说明理由．练习4.如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c(a≠0)与x轴交A(−1,0),B(−3,0)两点，与y轴交于点C(0,−3)，其顶点为D．(1)求该抛物线的解析式，并用配方法把解析式化为y=a(x−h)2+k的形式；(2)动点M从点D出发，沿抛物线对称轴方向向上以每秒1个单位的速度运动，运动时间为t，连接OM,BM，当t为何值时，△OMB为等腰三角形？练习5.如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n （m＜n）分别是方程x2﹣2x﹣3=0的两根．（1）求抛物线的解析式；（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E 两点（点D在y轴右侧），连接OD、BD．①当△OPC为等腰三角形时，求点P的坐标；②求△BOD 面积的最大值，并写出此时点D的坐标．25．（10分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过原点O，与x轴交于点A（5，0），第一象限的点C（m，4）在抛物线上，y轴上有一点B（0，10）．（Ⅰ）求抛物线的解析式及它的对称轴；（Ⅱ）点P（0，n）在线段OB上，点Q在线段BC上，若OP＝2BQ，且P A＝QA．求n 的值；（Ⅲ）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．19-红桥一模25．（10分）如图，抛物线y＝x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A，B，且B点的坐标为（2，0）．（1）求该抛物线的解析式．（2）若点P是AB上的一动点，过点P作PE∥AC，交BC于E，连接CP，求△PCE面积的最大值．（3）若点D为OA的中点，点M是线段AC上一点，且△OMD为等腰三角形，求M点的坐标．(17河北一模)25(10分）如图，己知抛物线y=x2+bx+c图象经过点A（﹣1，0），B（0，﹣3），抛物线与x轴的另一个交点为C．（1）求这个抛物线的解析式：（2）若抛物线的对称轴上有一动点D，且△BCD为等腰三角形（CB≠CD），试求点D的坐标；二、直角三角形1.情景：平面内有点A、B，要找到点P使得△ABP为直角三角形2.思想：分类讨论（1）A为顶点：∠A（过A做垂线）（2）B为顶点：∠B（过B做垂线）（3）P为顶点：∠C（AB为直径的圆）【注】1.等腰直角三角形，只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可例1.如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过矩形OABC的顶点A，B与x 轴交于点E，F且B，E两点的坐标分别为B(2，32)E(−1，0)(1)求二次函数的解析式；(2)在抛物线上是否存在点Q，使△QBF为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．练习1.如图，抛物线y=x2+bx+3顶点为P，且分别与x轴、y轴交于A、B两点，点A在点P的右侧，tan∠ABO=13(1)求抛物线的对称轴和PP的坐标．(2)在抛物线的对称轴上是否存在这样的点D，使△ABD为直角三角形？如果存在，求点D 的坐标；如果不存在，请说明理由．例2.如图，抛物线y=−x2+bx+c与x轴相交于AB两点，与y 轴相交与点C，且点B与点CC 的坐标分别为(3,0)，C(0,3)，点M是抛物线的顶点．(1)求二次函数的关系式(2)在MB上是否存在点P，过点P作PD⊥x轴于点D,OD=m,使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由练习2.如图，在平面直角坐标系中，直线y=−13x+2交x轴点P，交y轴于点A．抛物线y=x2+bx+c的图象过点E(−1,0)，并与直线相交于A、B两点．(1)求抛物线的解析式（关系式）；(2)过点A作AC⊥AB交x轴于点C，求点C的坐标；(3)除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M 的坐标；若不存在，请说明理由．练习3.如图，抛物线y=x2+bx+c与直线y=x﹣3交于A、B两点，其中点A在y轴上，点B坐标为（﹣4，﹣5），点P为y轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．（1）求抛物线的解析式；（2）以O，A，P，D为顶点的平行四边形是否存在？如存在，求点P的坐标；若不存在，说明理由．（3）当点P运动到直线AB下方某一处时，过点P作PM⊥AB，垂足为M，连接PA使△PAM为等腰直角三角形，请直接写出此时点P的坐标．（18东丽-一模）25.如图，在平面直角坐标系中，点A、B的坐标分别为（1，1）、（1，2），过点A、B分别作y轴的垂线，垂足为D、C，得到正方形ABCD，抛物线y=x2+bx+c经过A、C两点，点P为第一象限内抛物线上一点（不与点A重合），过点P分别作x轴y轴的垂线，垂足为E、F，设点P的横坐标为m，矩形PFOE与正方形ABCD重叠部分图形的周长为l．（1）直接写出抛物线所对应的函数表达式．（2）当矩形PFOE的面积被抛物线的对称轴平分时，求m的值．（3）当m＜2时，求L与m之间的函数关系式．（4）设线段BD与矩形PFOE的边交于点Q，当△FDQ为等腰直角三角形时，直接写出m的取值范围．三、平行四边形存在性问题类型一：1.情景：一直平面内三点A、B、C，求一点P使四边形ABCP为平行四边形2.思想：分类讨论（1）以AC为对角线：ABCP1（2）以AB为对角线：ACBP3（3）以BC为对角线：ACP2B【注】找到P点后，用平行四边形的判定定理，求等长线段，或利用等角度、平行线求坐标即可。

1、已知抛物线与x轴交于A、 B两点，与y轴交于点C．是否存在实数a，使得△ABC为直角三角形．若存在，请求出a的值；若不存在，请说明理由．由，解得，．∴点A、B的坐标分别为（-3，0），（，0）．∴，，．∴，，．〈ⅰ〉当时，∠ACB＝90°．由，得．解得．∴当时，点B的坐标为（，0），，，．于是．∴当时，△A BC为直角三角形．〈ⅱ〉当时，∠ABC＝90°．2：如图，抛物线与x轴交与A(1,0),B(-3，0)两点，顶点为D。

交Y轴于C，在抛物线第二象限图象上是否存在一点M，使△MBC是以∠BCM为直角的直角三角形，若存在，求出点P的坐标。

若没有，请说明理由抛物线y=-x^2+bx+c与x轴交予A(1,0),B(-3,0)两点,得-1+b+c=0-9-3b+c=0得b=-2,c=3该抛物线的解析式y=-x^2-2x+3点C为（0.3）△ABC的面积为1/2AB*OC=6设在抛物线第二象限图象上存在点M(x0,y0)使△MBC是以∠BCM为直角的直角三角形则x0<0,y0>0y0=-x0^2-2x0+3(1)再由MB^2=MC^2+BC^2得(x0+3)^2+(y0-0)^2=(x0-0)^2+(y0-3)^2+(0+3)^2+(3-0)^2(2)(3)由（1）和（2）可解得y0=3,x0=0或者y0=4，x0=-1又x0<0,y0>0所以y0=4，x0=-1在抛物线第二象限图象上存在点M(-1,4)使△MBC是以∠BCM为直角的直角三角形.3：（2012云南）如图，在平面直角坐标系中，直线交x轴于点P，交y轴于点A．抛物线的图象过点E（-1，0），并与直线相交于A、B两点（1）求抛物线的解析式（关系式）；（2）过点A作AC⊥AB交x轴于点C，求点C的坐标；（3）除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．解答：解：（1）直线解析式为y=x+2，令x=0，则y=2，∴A（0，2），∵抛物线y=x2+bx+c的图象过点A（0，2），E（﹣1，0），∴，解得．∴抛物线的解析式为：y=x2+x+2．（2）∵直线y=x+2分别交x轴、y轴于点P、点A，∴P（6，0），A（0，2），∴OP=6，OA=2．∵AC⊥AB，OA⊥OP，∴Rt△OCA∽Rt△OPA，∴，∴OC=，又C点在x轴负半轴上，∴点C的坐标为C（，0）．（3）抛物线y=x2+x+2与直线y=x+2交于A、B两点，令x2+x+2=x+2，解得x1=0，x2=，∴B（，）．如答图①所示，过点B作BD⊥x轴于点D，则D（，0），BD=，DP=6﹣=．点M在坐标轴上，且△MAB是直角三角形，有以下几种情况：①当点M在x轴上，且BM⊥AB，如答图①所示．设M（m，0），则MD=﹣m．∵BM⊥AB，BD⊥x轴，∴，即，解得m=，∴此时M点坐标为（，0）；②当点M在x轴上，且BM⊥AM，如答图①所示．设M（m，0），则MD=﹣m．∵BM⊥AM，易知Rt△AOM∽Rt△MDB，∴，即，化简得：m2﹣m+=0，解得：x1=，x2=，∴此时M点坐标为（，0），（，0）；（说明：此时的M点相当于以AB为直径的圆与x轴的两个交点）③当点M在y轴上，且BM⊥AM，如答图②所示．此时M点坐标为（0，）；④当点M在y轴上，且BM′⊥AB，如答图②所示．设M′（0，m），则AM=2﹣=，BM=，MM′=﹣m．易知Rt△ABM∽Rt△MBM′，∴，即，解得m=，∴此时M点坐标为（0，）．综上所述，除点C外，在坐标轴上存在点M，使得△MAB是直角三角形．符合条件的点M有5个，其坐标分别为：（，0）、（，0）、（，0）、（0，）或（0，）．4：（2012?河池）如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线经过A、B两点．（1）写出点A、点B的坐标；（2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的最大面积；（3）在（2）的条件下，抛物线上是否存在一点P，使得△PAM是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．解：（1）抛物线y=﹣x2+x+4中：令x=0，y=4，则 B（0，4）；令y=0，0=﹣x2+x+4，解得 x1=﹣1、x2=8，则 A（8，0）；∴A（8，0）、B（0，4）．△ABC中，AB=AC，AO⊥BC，则OB=OC=4，∴C（0，﹣4）．由A（8，0）、B（0，4），得：直线AC：y=﹣x+4；依题意，知：OE=2t，即 E（2t，0）；∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；S=S△ABC+S△PAB=×8×8+×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；∴当t=2时，S有最大值，且最大值为64．（3）∵PM∥y轴，∴∠AMP=∠ACO＜90°；而∠APM是锐角，所以△PAM若是直角三角形，只能是∠PAM=90°；由A（8，0）、C（0，﹣4），得：直线AC：y=x﹣4；所以，直线AP可设为：y=﹣2x+h，代入A（8，0），得：﹣16+h=0，h=16∴直线AP：y=﹣2x+16，联立抛物线的解析式，得：，解得、∴存在符合条件的点P，且坐标为（3，10）．5：（2012?海南）如图，顶点为P（4，-4）的二次函数图象经过原点（0，0），点A在该图象上，OA交其对称轴l于点M，点M、N关于点P对称，连接AN、ON，（1）求该二次函数的关系式；（2）若点A在对称轴l右侧的二次函数图象上运动时，请解答下面问题：①证明：∠ANM=∠ONM；②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标；如果不能，请说明理由．1）∵二次函数图象的顶点为P（4，－4），∴设二次函数的关系式为。

2023年九年级中考数学复习：二次函数综合题（特殊三角形问题）1．抛物线y＝ax2＋c交x轴于A、B（1，0）两点，且经过（2，3）．(1)求抛物线的解析式；(2)如图1，直线y＝kx＋3交y轴于点G，交抛物线y＝ax2＋c于点E和F，F在y轴右侧，若△GOF的面积为△GOE面积的2倍，求k值；(3)如图2，点P是第二象限的动点，分别连接P A、PB，并延长交直线y=－2于M、N 两点. 若M、N两点的横坐标分别为m、n，试探究m、n之间的数量关系．2．如图，已知抛物线2=++与直线y=0.5x＋3相交于A，B两点，交△轴于C，0.5y x bx cD两点，连接AC，BC，已知A（0，3），C（－3，0）.(1)求抛物线的表达式；(2)在抛物线对称轴l上找一点M，使|MB一MD|的值最大，并求出这个最大值；(3)点P为y轴右侧抛物线上的一动点，连接P A，过点P作PQ△P A交y轴于点Q，是否存在点P，使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由.3．如图，抛物线与x轴交于A和B两点（点B位于点A右侧），与y轴交于点C，对称轴是直线x=2，且OA=1，OC=3，连接AC，BC．(1)求此抛物线的函数解析式；(2)设抛物线的顶点为点P，请在x轴上找到一个点D，使以点P、B、D为顶点的三角形与△ABC相似？(3)此抛物线的对称轴和以AC为直径的圆是什么位置关系？如果是相切或相交，请直接写出切点或交点的坐标（不必写演推过程）；如果是相离，请简要说明理由．4．如图1，已知抛物线y=ax2+bx+3与x轴分别交于A(−3，0)，B(1，0)两点，与y轴交于点C，点D为抛物线的顶点，连接AD、CD、AC、BC．(1)请直接写出抛物线的表达式及顶点D的坐标；(2)求证：△ACD是直角三角形；(3)判断△ACB和△OAD的数量关系，并说明理由；(4)如图2，点F是线段AD上一个动点，以A，F，O为顶点的三角形是否与△ABC相似？若相似，请直接写出点F的坐标；若不相似，请说明理由．5．抛物线y＝ax2﹣2x+c经过点A(3，0)，点C(0，﹣3)，直线y＝﹣x+b经过点A，交抛物线于点E．抛物线的对称轴交AE于点B，交x轴于点D，交直线AC于点F．(1)求抛物线的解析式；(2)如图△，点P 为直线AC 下方抛物线上的点，连接P A ，PC ，△BAF 的面积记为S 1，△P AC 的面积记为S 2，当S 2＝38S 1时．求点P 的横坐标；(3)如图△，连接CD ，点Q 为平面内直线AE 下方的点，以点Q ，A ，E 为顶点的三角形与△CDF 相似时（AE 与CD 不是对应边），请直接写出符合条件的点Q 的坐标． 6．如图，抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ，与y 轴交于点C ，联结AC 、BC ．(1)求该抛物线的表达式及顶点D 的坐标；(2)如果点P 在抛物线上，CB 平分ACP ∠，求点P 的坐标：(3)如果点Q 在抛物线的对称轴上，DBQ 与ABC 相似．求点Q 的坐标．7．如图1，已知二次函数y ＝ax2＋bx ＋c （a ≠0）的图象与x 轴交于A （﹣1，0），B （3，0）两点，与y 轴交于点C （0，﹣2），顶点为D ，对称轴交x 轴于点E ．(1)求该二次函数的解析式；(2)设M 为该抛物线上直线BC 下方一点，过点M 作x 轴的垂线，交线段BC 于点N ，线段MN 是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由；(3)连接CE （如图2），设点P 是位于对称轴右侧该抛物线上一点，过点P 作PQ △x 轴，垂足为Q ．连接PE ，请求出当△PQE 与△COE 相似时点P 的横坐标．8．如图，直线y kx b =+与x 轴、y 轴分别交于A ，B 两点，抛物线2y ax bx c =++经过A ，B 两点，点C 的坐标为()1,0-，3AO CO ==，点C 关于点B 的对称点M 刚好落在抛物线上，连接AM ．(1)求点M 的坐标；(2)求抛物线的解析式；(3)过点M 作MD 平行于y 轴交AB 于点D ，若点E 为抛物线上的一点，点F 在x 轴上，连接AE ，AF ，EF ．是否存在点F 使得△ADM 与△AEF 相似？若存在，请直接写出点F 的坐标；若不存在，请说明理由．9．如图1，已知在平面直角坐标系xOy 中，四边形OABC 是边长为3的正方形，其中顶点A ，C 分别在x 轴的正半轴和y 轴的正半轴上，抛物线2y x bx c =-++经过A ，C 两点，与x 轴交于另一个点D ．(1)△求点A ，B ，C 的坐标；△求b ，c 的值．(2)若点P 是边BC 上的一个动点，连结AP ，过点P 作PM △AP ，交y 轴于点M （如图2所示）．当点P 在BC 上运动时，点M 也随之运动．设BP ＝m ，CM ＝n ，试用含m 的代数式表示n ，并求出n 的最大值．10．平面直角坐标系中，已知抛物线1C ：()21y x m x m =-++-（m 为常数）与x 轴交于点A ，B 两点（点A 在点B 左边），与y 轴交于点C ．(1)若4m =，求点A ，B ，C 的坐标；(2)如图1，在（1）的条件下，D 为抛物线x 轴上方一点，连接BD ，若90DBA ACB ∠∠+=︒，求点D 的坐标；(3)如图2，将抛物线1C 向左平移n 个单位长度（0n >）与直线AC 交于M ，N （点M 在点N 右边），若2AM CN =，求m ，n 之间的数量关系．11．如图，直线y x n =-+与x 轴交于点()3,0A ，与y 轴交于点B ，抛物线2y x bx c =-++经过点A ，B ．(1)求n 的值及抛物线的解析式；(2)(),0E m 为x 轴上一动点，过点E 作ED x ⊥轴，交直线AB 于点D ，交抛物线于点P ，连接BP ．△点E 在线段OA 上运动，若BPD △与ADE 相似，求点E 的坐标；△若抛物线的顶点为Q ，AQ 与CB 的延长线交于点H ，点E 在x 轴的正半轴上运动，若PBD CBO H ∠+∠=∠．请求写出m 的值．12．如图1，平面直角坐标系xOy 中，直线y ＝－12x －2与x 轴交于点A ，与y 轴交于点C ．抛物线y ＝14x 2＋bx ＋c 经过点A 、点C ，且与x 轴交于另一点B ，连接BC ．(1)求抛物线的解析式；(2)点P 是抛物线上一动点．△当点P 在直线AC 下方的抛物线上运动时，如图2，连接AP ，CP ．求四边形ABCP 面积的最大值及此时点P 的坐标；△当点P 在x 轴上方的抛物线上运动时，过点P 作PM △x 轴于点M ，连接BP ．是否存在点P ，使△PMB 与△AOC 相似？若存在，请直接写出点P 的坐标；若不存在，请说明理由．13．如图，抛物线y 2b c x ++与x 轴交于点A 、B ，点A 、B 分别位于原点的左、右两侧，BO ＝3AO ＝3，过点B 的直线与y 轴正半轴和抛物线的交点分别为C 、D ，BC．(1)求b、c的值；(2)求直线BD的直线解析式；(3)点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当△ABD与△BPQ相似时，请直接写出所有满足条件的点Q的坐标．14．如图，抛物线23(0)y ax bx a=+-≠的顶点E的横坐标为1，与x轴交于A、B两点，与y轴交于点C，直线113y x=-+过点B，与y轴交于点D．(1)求抛物线的解析式；(2)证明：ABD CBE∠=∠；(3)是否存在点1O，使点1O到A，B，C，D的距离都相等，若存在，求出点1O坐标，若不存在，请说明理由．(4)设抛物线与直线DB另一交点为Q，F为线段BQ上一点（不含端点），连接AF，一动点P从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FQ个单位的速度运动到Q后停止，当点F的坐标是多少时，点P在整个运动过程中用时最少？（直接写出答案）15．如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于点A 、B ，与y 轴交于点C ，且OC ＝2OB ＝6OA ＝6，点P 是第一象限内抛物线上的动点．(1)求抛物线的解析式；(2)连接BC 与OP ，交于点D ，当PD ：OD 的值最大时，求点P 的坐标；(3)点P 在抛物线上运动，点N 在y 轴上运动，是否存在点P 、点N ．使△CPN ＝90°，且△CPN 与△BOC 相似，若存在，请直接写出点P 的坐标，若不存在，说明理由．16．在平面直角坐标系xOy 中，抛物线y ＝﹣x 2+bx +c 与x 轴分别交于点A ，点B （3，0），与y 轴交于点C （0，3）．(1)求抛物线的解析式；(2)如图1，连接BC ，点D 是直线BC 上方抛物线上一动点，连接AD 交BC 于点E ，若AE ＝2ED ，求点D 的坐标；(3)直线y ＝kx ﹣2k +1与抛物线交于M ，N 两点，取点P （2，0），连接PM ，PN ，求△PMN 面积的最小值．17．综合与探究如图，直线3y x =-+与x 轴，y 轴分别交于B ，C 两点，抛物线2y x bx c =-++经过点B ，C ，与x 轴的另一交点为A ，顶点为D ．(1)求抛物线的解析式及顶点D的坐标．(2)连接CD，BD，求点D到BC的距离h．(3)P为对称轴上一点，在抛物线上是否存在点Q，使得PDQ与BOC相似？若存在，请直接写出Q点坐标；若不存在，请说明理由．18．如图，已知直线223y x=-与x轴交于点A，与y轴交于点B，抛物线226y x bx=-++经过点A，与x轴的另一个交点为C，交y轴于点D．(1)求抛物线的函数表达式及点D的坐标；(2)点M是y轴上的点，在y轴右侧的抛物线上是否存在点P，使得PMD△与BOC相似，且点M与点O为对应点，若存在，请求出点P的坐标，若不存在，请说明理由．19．如图，在平面直角坐标系中，直线y=2x+6与x轴交于点A，与y轴交点C，抛物线y=-2x2+bx+c过A，C两点，与x轴交于另点B．(1)求抛物线的解析式．(2)在直线AC 上方的抛物线上有一动点E ，连接BE ，与直线AC 相交于点F ，当EF =12BF 时，求sin△EBA 的值．(3)点N 是抛物线对称轴上一点，在(2)的条件下，若点E 位于对称轴左侧，在抛物线上是否存在一点M ，使以M ，N ，E ，B 为顶点的四边形是平行四边形？若存在，直接写出点M 的坐标；若不存在，请说明理由．20．如图，一次函数3y x =-+的图象与x 轴和y 轴分别交于点B 和点C ，二次函数2y x bx c =-++的图象经过B ，C 两点，并与x 轴交于点A ．点(),0M m 是线段OB 上一个动点（不与点O 、B 重合），过点M 作x 轴的垂线，分别与二次函数图象和直线BC 相交于点D 和点E ，连接CD ．(1)求这个二次函数的解析式．(2)△求DE 、CE 的值（用含m 的代数式表示）．△当以C ，D ，E 为顶点的三角形与△ABC 相似时，求m 的值．(3)点F 是平面内一点，是否存在以C ，D ，E ，F 为顶点的四边形为菱形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．参考答案：1．(1)21y x =- (2)k =(3) 1.-2．(1)215322y x x =++(3)在点P （1，6）3．(1)y =x 2－4x +3(2)点D 的坐标是（0，0）或（73，0） (3)相交，交点的坐标是（2，1）或（2，2）4．(1)抛物线解析式为y =-x 2-2x +3；顶点D 的坐标为（-1，4）；(2)见解析(3)△OAD =△ACB(4)相似，F 点的坐标为（-65，185）或（-2，2）．5．(1)y ＝x 2﹣2x ﹣3(2)P 352(3)Q 点坐标为(﹣7，5)或(﹣12，5)或(3，﹣10)或(3，﹣5)6．(1)2=+43y x x --，(21)D ， (2)111639⎛⎫ ⎪⎝⎭，- (3)(2，−2)或12,3⎛⎫ ⎪⎝⎭7．(1)224233y x x =--(2)线段MN 存在最大值，最大值为32(3)点P 的横坐标为5或28．(1)(M(2)2y x x =(3)存在，()()()()()11,0,3,0,,0,5,0,7,0,13,03⎛⎫-- ⎪⎝⎭9．(1)△A (3，0)，B (3，3)，C (0，3)；△23b c =⎧⎨=⎩ (2)2133324n m ⎛⎫=--+ ⎪⎝⎭（0≤m ≤3）；3410．(1)A （1，0），B （4，0），C （0，﹣4）(2)D （83，209） (3)93m n =-11．(1)n =3，y =-x 2+2x +3．(2)△（1，0）或（2，0）．△m =5或73．12．(1)211242y x x =+- (2)△四边形ABCP 面积的最大值为8，此时点P 为（－2，－2）；△存在符合条件的点P ，点P 坐标为（－6，4）或（－12，28）或（4，4）13．(1)132b c ⎧=-⎪⎪⎨⎪=-⎪⎩(2)y=+(3)Q 1（，0）、Q 2（0）、Q 3，0）、Q 4（，0） 14．(1)2 2 3y x x =--(2)见解析(3)存在点()111O -,，使点P 到A ，B ，C ，D 的距离都相等(4)F 的坐标为41,3⎛⎫- ⎪⎝⎭时，点P 在整个运动过程中用时最少15．(1)y ＝﹣2x 2+4x +6(2)点P 的坐标为315(,)22(3)存在，点P 的坐标分别为(3，0)或(1，8)或939(,)48或755(,)4816．(1)y ＝﹣x 2+2x +3(2)（1，4）或（2，3）17．(1)223y x x =-++，顶点D (1，4)(2)h =(3)Q （0，3）或（2，3）18．(1)2246y x x =-++；(0,6)D(2)存在，点P 的坐标为755,48⎛⎫ ⎪⎝⎭或939,48⎛⎫ ⎪⎝⎭或(1,8)或(3,0)19．(1)抛物线的解析式为y =-2x 2-4x +6；(2)sin△EBA ； (3)M 的坐标为（2，-10）或（-4，-10）或（0，6）．20．(1)223y x x =-++(2)△23DE m m =-，CE ；△m 的值为32或53(3)存在以C ，D ，E ，F 为顶点的四边形为菱形，点M 的坐标为(1，0)或(2，0)或(3，0)．。

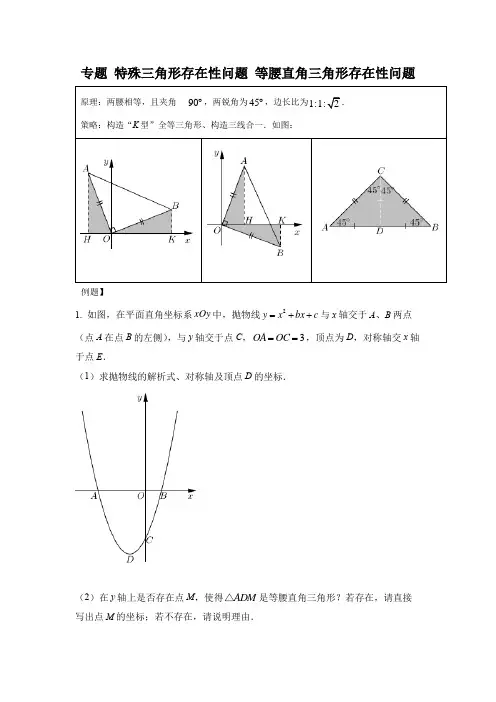
专项12 二次函数与几何综合-特殊三角形存在问题等腰三角形的存在性问题【方法1 几何法】“两圆一线”（1）以点A 为圆心，AB 为半径作圆，与x 轴的交点即为满足条件的点C ，有AB=AC ；（2）以点B 为圆心，AB 为半径作圆，与x 轴的交点即为满足条件的点C ，有BA=BC ；（3）作AB 的垂直平分线，与x 轴的交点即为满足条件的点C ，有CA=CB ．注意：若有重合的情况，则需排除．以点 C 1 为例，具体求点坐标：过点A 作AH ⊥x 轴交x 轴于点H ，则AH=1， 又32121131311==-=∴=HC AC ，()03211，坐标为故点-C 类似可求点 C 2 、C 3、C 4 ．关于点 C 5 考虑另一种方法．【方法2 代数法】点-线-方程表示点：设点C 5坐标为(m ,0)，又A （1,1）、B （4,3），表示线段：11-m 225+=）（AC 94-m 225+=）（BC 联立方程：914-m 1-m 22+=+）（）（，623m =解得：，），坐标为（故点06232C直角三角形的存在性【方法1 几何法】“两线一圆”（1）若∠A 为直角，过点 A 作 AB 的垂线，与 x 轴的交点即为所求点 C ；（2）若∠B 为直角，过点 B 作 AB 的垂线，与 x 轴的交点即为所求点 C ；（3）若∠C 为直角，以 AB 为直径作圆，与 x 轴的交点即为所求点 C ．（直径所对的圆周角为直角）如何求得点坐标？以C 2为例：构造三垂直．），坐标为（故代入得：坐标得、由易证0213232222C C C BN AM B A N MBBN AM BN AMB ===∆≈∆()），坐标为（，，坐标为故或故又即代入得：，设，坐标得、由易证求法相同，如下：、040231a ,4a ,3ab ,3ab 1N a,31,4333333343C C C C C C C C C C b bM BN AM B A NBM N AMNB AM ==+=======∆≈∆【方法2 代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==，解得：）代入得方程（，，，）表示线段：（）；，（）、，（），又坐标为（）表示点：设（：不妨来求下）（）（）（）（BC C C C A AB B A【考点1 等腰角形的存在性】【典例1】（2020•泰安）如图，在平面直角坐标系中，二次函数y＝ax2+bx+c交x轴于点A （﹣4，0）、B（2，0），交y轴于点C（0，6），在y轴上有一点E（0，﹣2），连接AE．（1）求二次函数的表达式；（2）抛物线对称轴上是否存在点P，使△AEP为等腰三角形？若存在，请直接写出所有P点的坐标，若不存在，请说明理由．【答案】（1）y＝，（2）m＝时，△ADE的面积取得最大值为（3）点P坐标为：（﹣1，1），（﹣1，），（﹣1，﹣2）【解答】解：（1）∵二次函数y＝ax2+bx+c经过点A（﹣4，0）、B（2，0），C（0，6），∴，解得，所以二次函数的解析式为：y＝，（2）y＝的对称轴为x＝﹣1，设P（﹣1，n），又E（0，﹣2），A（﹣4，0），可求P A2＝9+n2，PE2＝1+（n+2）2，AE2＝16+4＝20，当P A2＝PE2时，9+n2＝1+（n+2）2，解得，n＝1，此时P（﹣1，1）；当P A2＝AE2时，9+n2＝20，解得，n＝，此时点P坐标为（﹣1，）；当PE2＝AE2时，1+（n+2）2＝20，解得，n＝﹣2，此时点P坐标为：（﹣1，﹣2）．综上所述，P点的坐标为：（﹣1，1），（﹣1，），（﹣1，﹣2）．【变式1-2】（2020•贵港）如图，已知二次函数y＝ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．（1）求这个二次函数的表达式；（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与线段BC 交于点M，连接PC．当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．【答案】（1）y＝x2﹣2x﹣3 （2）①n＝时，PM最大＝②P（3﹣，2﹣4）或（2，﹣3）．【解答】解：（1）将A，B，C代入函数解析式，得，解得，这个二次函数的表达式y＝x2﹣2x﹣3；（2）解法一：当PM＝PC时，（﹣n2+3n）2＝n2+（n2﹣2n﹣3+3）2，解得n1＝n2＝0（不符合题意，舍），n3＝2，n2﹣2n﹣3＝﹣3，P（2，﹣3）．当PM＝MC时，（﹣n2+3n）2＝n2+（n﹣3+3）2，解得n1＝0（不符合题意，舍），n2＝3﹣，n3＝3+（不符合题意，舍），n2﹣2n﹣3＝2﹣4，P（3﹣，2﹣4）．综上所述：P（3﹣，2﹣4）或（2，﹣3）．解法二：当PM＝PC时，∵BC：y＝x﹣3∴∠ABC＝45°∵PH⊥AB∴∠BMH＝∠CMP＝45°∴PM＝PC时，△CPM为等腰直角三角形，CP∥x轴设P（n，n2﹣2n﹣3），则CP＝nMP＝﹣n2+3n∴n＝﹣n2+3n解得n＝0（舍去）或n＝2，∴P（2，﹣3）当PM＝CM时，设P（n，n2﹣2n﹣3），则＝﹣n2+3n＝﹣n2+3n∵n＞0∴n＝﹣n2+3n解得n＝3﹣∴P（3﹣，2﹣4）综上所述：P（3﹣，2﹣4）或（2，﹣3）【变式1-2】（2022•澄海区模拟）如图，抛物线y＝ax2+bx+c交x轴于A、B两点，交y轴于点C，点A的坐标为（﹣1，0），点C坐标为（0，3），对称轴为x＝1．点M为线段OB上的一个动点（不与两端点重合），过点M作PM⊥x轴，交抛物线于点P，交BC 于点Q．（1）求抛物线及直线BC的表达式；（2）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线对称轴为x＝1，点B与A（﹣1，0）关于直线x＝1对称，∴B（3，0），设y＝a（x﹣3）（x+1），把C（0，3）代入得：﹣3a＝3，解得：a＝﹣1，∴y＝﹣（x﹣3）（x+1）＝﹣x2+2x+3，设直线BC的解析式为y＝kx+d，则，解得：，∴直线BC的解析式为y＝﹣x+3，故抛物线解析式为y＝﹣x2+2x+3，直线BC的解析式为y＝﹣x+3；（2）存在，设Q（m，﹣m+3）（0＜m＜3），∵A（﹣1，0），C（0，3），∴AC2＝OA2+OC2＝12+32＝10，AQ2＝（m+1）2+（﹣m+3）2＝2m2﹣4m+10，CQ2＝m2+m2＝2m2，∵以A，C，Q为顶点的三角形是等腰三角形，∴AC＝AQ或AC＝CQ或AQ＝CQ，当AC＝AQ时，10＝2m2﹣4m+10，解得：m＝0（舍去）或m＝2，∴Q（2，1）；当AC＝CQ时，10＝2m2，解得：m＝﹣（舍去）或m＝，∴Q（，3﹣）；当AQ＝CQ时，2m2﹣4m+10＝2m2，解得：m＝，∴Q（，）；综上所述，点Q的坐标为（2，1）或（，3﹣）或（，）．【考点2 直角三角形的存在性】【典例2】（2021秋•建华区期末）抛物线y＝x2+bx+c经过A、B（1，0）、C（0，﹣3）三点．点D为抛物线的顶点，连接AD、AC、BC、DC．（1）求抛物线的解析式；（2）在y轴上是否存在一点E，使△ADE为直角三角形？若存在，请你直接写出点E的坐标；若不存在，请说明理由．【解答】解（1）∵抛物线y＝x2+bx+c经过B（1，0）、C（0，﹣3），∴，解得，∴抛物线的解析式为：y＝x2+2x﹣3．（4）在y轴上存在点E，使△ADE为直角三角形，理由如下：∵抛物线的解析式为y＝x2+2x﹣3＝（x+1）2﹣4，∴D（﹣1，﹣4），设E点坐标为（0，m），∴AE2＝m2+9，DE2＝m2+8m+17，AD2＝20，当∠EAD＝90°时，有AE2+AD2＝DE2，∴m2+9+20＝m2+8m+17，解得m＝，∴此时点E的坐标为（0，）；当∠ADE＝90°时，DE2+AD2＝AE2，m2+8m+17+20＝m2+9，解得m＝﹣，∴此时点E的坐标为（0，﹣）；当∠AED＝90°时，AE2+DE2＝AD2，m2+9+m2+8m+17＝20，解得m＝﹣1或m＝﹣3，∴此时点E的坐标为（0，﹣1）或（0，﹣3）．综上所述，符合题意的点E的坐标为（0，）或（0，﹣）或（0，﹣1）或（0，﹣3）．【变式2-1】（2022•灞桥区校级模拟）如图，抛物线与x轴交于点A（1，0），B（3，0），与y轴交于点C（0，3）．（1）求二次函数的表达式及顶点坐标；（2）连接BC，在抛物线的对称轴上是否存在一点E，使△BCE是直角三角形？若存在，请直接写出点E的坐标；若不存在，请说明理由．【解答】解：（1）设抛物线的解析式为y＝a（x﹣1）（x﹣3），将点C（0，3）代入y＝a（x﹣1）（x﹣3），∴3a＝3，∴a＝1，∴y＝（x﹣1）（x﹣3）＝x2﹣4x+3，∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴顶点为（2，﹣1）；（2）存在一点E，使△BCE是直角三角形，理由如下：∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴抛物线的对称轴为直线x＝2，设E（2，t），∵△BCE是直角三角形，∴BE⊥CE，∵B（3，0），C（0，3），∴BC＝3，BE＝，CE＝，①当BC为斜边时，∴18＝（）2+（）2，解得t＝，∴E点坐标为（2，）或（2，）；②当BE为斜边时，∴18+（）2＝（）2，解得t＝5，∴E点坐标为（2，5）；③当CE为斜边时，∴18+（）2＝（）2，解得t＝﹣1，∴E点坐标为（2，﹣1）；综上所述：E点坐标为（2，）或（2，）或（2，5）或（2，﹣1）．【变式2-2】（2022•碑林区校级四模）如图，在平面直角坐标系中，抛物线C1：y＝ax2+bx+c 交x轴于点A（﹣5，0），B（﹣1，0），交y轴于点C（0，5）．（1）求抛物线C1的表达式和顶点D的坐标．（2）将抛物线C1关于y轴对称的抛物线记作C2，点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形，求点E的坐标．【解答】解：（1）将点A（﹣5，0），B（﹣1，0），C（0，5）代入y＝ax2+bx+c，∴，解得，∴y＝x2+6x+5，∵y＝x2+6x+5＝（x+3）2﹣4，∴顶点D（﹣3，﹣4）；（2）设抛物线C2上任意一点（x，y），则（x，y）关于y轴对称的点为（﹣x，y），∵点（﹣x，y）在抛物线C1上，∴抛物线记作C2的解析式为y＝x2﹣6x+5，设E（t，t2﹣6t+5），过点D作DG⊥x轴交于点G，过点E作EH⊥x轴交于点H，∵∠DOE＝90°，∴∠GOD+∠HOE＝90°，∵∠GOD+∠GDO＝90°，∴∠HOE＝∠GDO，∴△GDO∽△HOE，∴＝，∵DG＝4，GO＝3，HE＝﹣t2+6t﹣5，OH＝t，∴＝，∴t＝4或t＝，∴E（4，﹣3）或E（，﹣）．【变式2-3】（2022•武功县模拟）如图，经过点A（2，6）的直线y＝x+m与y轴交于点B，以点A为顶点的抛物线经过点B，抛物线的对称轴为直线l．（1）求点B的坐标和抛物线的函数表达式；（2）在l右侧的抛物线上是否存在点P，使得以P、A、B为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵直线y＝x+m经过点A（2，6），∴2+m＝6，解得m＝4，即y＝x+4．令x＝0，得y＝4，即点B的坐标为（0，4）．∵点A（2，6）为抛物线的顶点，∴可设抛物线的函数表达式为y＝a（x﹣2）2+6（a≠0），将点B（0，4）代入，得4＝4a+6，解得，∴抛物线的函数表达式为．∴点B的坐标为（0，4），抛物线的函数表达式为y＝﹣x2+2x+4；（2）∵点A（2，6）为抛物线的顶点，∴抛物线的对称轴l：x＝2．①当AB为该等腰三角形的底边时：如图，点P在P2的位置．过点A作AC⊥y轴于点C，过点P2作P2D⊥AC交CA的延长线于点D，作P2E⊥y轴于点E，连接P2A，P2B，则P2A＝P2B，∠D＝∠P2EB＝90°．∵A（2，6），B（0，4），AC⊥BC，∴AC＝BC＝2，∴△ABC是等腰直角三角形，∴∠CAB＝∠CBA．∵P2A＝P2B，∴∠P2AB＝∠P2BA，∴180°﹣∠CAB﹣∠P2AB＝180°﹣∠CBA﹣∠P2BA，即∠P2AD＝∠P2BE．在△P2AD和△P2BE中，∠D＝∠P2EB，∠P2AD＝∠P2BE，P2A＝P2B，∴△P2AD≌△P2BE（AAS），∴P2D＝P2E．设，则P2E＝m，，∴，解得（舍去）或，∴；②当AB为该等腰三角形的腰时，作点B关于l的对称点P1，由抛物线的对称性可知，AB＝AP1．∵B（0，4），抛物线的对称轴为直线x＝2，∴P1（4，4）．综上可知，在l右侧的抛物线上存在点P，使得以P、A、B为顶点的三角形是等腰三角形，点P的坐标为（4，4）或．【考点3 等腰直角三角形的存在性】【典例3】（2022•黔东南州一模）抛物线y＝ax2+bx﹣经过点（1，﹣1），现将一块等腰直角三角板ABC（∠ACB＝90°）按照如图的方式放在第二象限，斜靠在两坐标轴上，且点A、C坐标分别为（0，2）、（﹣1，0）．B点在抛物线y＝ax2+bx﹣图象上．（1）求点B的坐标：（2）求抛物的解析式；（3）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求出点P的坐标：若不存在，请说明理由．【解答】解：（1）过点B作BD⊥x轴，垂足为D．∵∠BCD+∠ACO＝90°，∠ACO+∠CAO＝90°，∴∠BCD＝∠CAO，又∵∠BDC＝∠COA＝90°，CB＝AC，∴△BCD≌△CAO（AAS），∴BD＝OC＝1，CD＝OA＝2，∴点B的坐标为（﹣3，1）；（2）抛物线y＝ax2+bx﹣经过点（1，﹣1），点B（﹣3，1），则，解得，所以抛物线的解析式为y＝x2+x﹣；（3）假设存在点P，使得△ACP仍然是以AC为直角边的等腰直角三角形：①若以点C为直角顶点；则延长BC至点P1，使得P1C＝BC，得到等腰直角三角形△ACP1，过点P1作P1M⊥x轴，∵CP1＝BC，∠MCP1＝∠BCD，∠P1MC＝∠BDC＝90°，∴△MP1C≌△DBC（AAS），∴CM＝CD＝2，P1M＝BD＝1，∵OC＝1，∴OM＝1，∴P1（1，﹣1）；②若以点A为直角顶点；则过点A作AP2⊥CA，且使得AP2＝AC，得到等腰直角三角形△ACP2，过点P2作P2N⊥y轴，同理可证△AP2N≌△CAO，∴NP2＝OA＝2，AN＝OC＝1，∴点P2（2，1），③以A为直角顶点的等腰Rt△ACP的顶点P有两种情况．即过点A作直线L⊥AC，在直线L上截取AP＝AC时，点P可能在y轴右侧，即现在解答情况②的点P2；点P也可能在y轴左侧，即还有第③种情况的点P3．因此，然后过P3作P3G⊥y轴于G，同理：△AGP3≌△CAO，∴GP3＝OA＝2，AG＝OC＝1，∴P3为（﹣2，3）；经检验，点P1（1，﹣1）与在抛物线y＝x2+x﹣上，点P2（2，1）点P3（﹣2，3）都不在抛物线y＝x2+x﹣上．综上，存在，点P的坐标为（1，﹣1）．【变式1-1】（2022•兴宁区校级模拟）如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B（8，0），点A为抛物线的顶点．（1）求二次函数的表达式；（2）在抛物线的对称轴上是否存在点M，使△ABM是等腰三角形？如果存在，请求出点M的坐标．如果不存在，请说明理由；【解答】解：（1）由题意，解得：，∴二次函数的表达式为y＝x2﹣2x；（2）过点A作直线AF⊥x轴于点F，由（1）得y＝（x﹣4）2﹣4，∴抛物线的顶点A（4，﹣4），①AM＝BM，∵B（8，0），∴BF＝4，∵∠AFB＝90°，AF＝BF＝4，∴△ABF是等腰直角三角形，∴M在点F处，△ABM是等腰直角三角形，此时M为（4，0），②AB＝AM，由①得△ABF是等腰直角三角形，BF＝4，∴AB＝＝＝4，∴M为（4，﹣4﹣4）或（4，﹣4+4），③AB＝BM，∵AB＝BM，BF⊥AM，∴MF＝AF，∴M为（4，4），综上所述，M为（4，0），（4，﹣4﹣4）或（4，﹣4+4）或（4，4）；【变式3-2】（2022•禅城区二模）如图，抛物线经过原点O，对称轴为直线x＝2且与x轴交于点D，直线l：y＝﹣2x﹣1与y轴交于点A，与抛物线有且只有一个公共点B，并且点B在第四象限，直线l与直线x＝2交于点C．（1）连接AD，求证：AD⊥AC．（2）求抛物线的函数关系式．（3）在直线l上有一点动点P，抛物线上有一动点Q，当△PBQ是以PQ为斜边的等腰直角三角形时，直接写出此时点P的坐标．【解答】解：（1）如图1，过点C作CE⊥y轴于点E，则∠AEC＝∠DOA＝90°，∵直线y＝﹣2x﹣1与y轴交于点A，与直线x＝2交于点C，∴A（0，﹣1），C（2，﹣5），∴E（0，﹣5），∴OA＝1，OD＝2，CE＝2，AE＝4，∴＝，＝＝，∴＝，∵∠AEC＝∠DOA，∴△AEC∽△DOA，∴∠CAE＝∠ADO，∵∠ADO+∠DAO＝90°，∴∠CAE+∠DAO＝90°，∴∠DAC＝180°﹣（∠CAE+∠DAO）＝180°﹣90°＝90°，∴AD⊥AC．（2）设抛物线的函数关系式为y＝ax2+bx，∵对称轴为直线x＝2，∴＝2，∴b＝﹣4a，∴y＝ax2﹣4ax，由ax2﹣4ax＝﹣2x﹣1，整理得ax2+（2﹣4a）x+1＝0，∵直线y＝﹣2x﹣1与抛物线有且只有一个公共点B，∴Δ＝（2﹣4a）2﹣4a＝0，解得：a1＝，a2＝1，当a＝时，抛物线解析式为y＝x2﹣x，联立得x2﹣x＝﹣2x﹣1，解得：x1＝x2＝﹣2，∴B（﹣2，3）与点B在第四象限矛盾，故a＝不符合题意，舍去，当a＝1时，y＝x2﹣4x，联立得x2﹣4x＝﹣2x﹣1，解得：x1＝x2＝1，∴B（1，﹣3），点B在第四象限符合题意，∴a＝1，∴该抛物线的函数关系式为y＝x2﹣4x．（3）如图2，过点B作BQ⊥AB交抛物线于点Q，作GH∥x轴交y轴于点G，过点Q 作QH⊥GH，则∠AGB＝∠BHQ＝∠ABQ＝90°，∴∠ABG+∠QBH＝∠ABG+∠BAG＝90°，∴∠QBH＝∠BAG，∴△ABG∽△BQH，∴＝，设Q（t，t2﹣4t），∵A（0，﹣1），B（1，﹣3），∴AG＝2，BG＝1，BH＝t﹣1，QH＝t2﹣4t+3，∴＝，解得：t＝1（舍去）或t＝，∴BH＝﹣1＝，QH＝（）2﹣4×+3＝，过点B作EF∥y轴，过点P1作P1E⊥EF，过点P2作P2F⊥EF，∵△PBQ是以PQ为斜边的等腰直角三角形，∴P1B＝BQ＝P2B，∵∠P1BE+∠EBQ＝∠EBQ+∠QBH＝90°，∴∠P1BE＝∠QBH，∵∠BEP1＝∠BHQ＝90°，∴△BEP1≌△BHQ（AAS），∴EP1＝QH＝，BE＝BH＝，∴P1（﹣，﹣），同理可得：P2（，﹣），综上，点P的坐标为P1（﹣，﹣），P2（，﹣）．1．（2022•榆阳区一模）如图，已知抛物线y＝mx2+4x+n与x轴交于A、B两点，与y轴交于点C．直线y＝x﹣3经过B，C两点．（1）求抛物线的函数表达式；（2）抛物线的顶点为M，在该抛物线的对称轴l上是否存在点P，使得以C，M，P为顶点的三角形是等腰三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）y＝x﹣3中，令x＝0，则y＝﹣3，∴C（0，﹣3），令y＝0，则x＝3，∴B（3，0），将C（0，﹣3），B（3，0）代入y＝mx2+4x+n中，∴，解得，∴y＝﹣x2+4x﹣3；（2）存在点P，使得以C，M，P为顶点的三角形是等腰三角形，理由如下：∵y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴M（2，1），对称轴为直线x＝2，设P（2，t），∴MP＝|t﹣1|，MC＝2，CP＝，①当MP＝MC时，|t﹣1|＝2，∴t＝2+1或t＝﹣2+1，∴P（2，2+1）或（2，﹣2+1）；②当MP＝CP时，|t﹣1|＝，解得t＝﹣，∴P（2，﹣）；③当MC＝CP时，2＝，解得t＝1（舍）或t＝﹣7，∴P（2，7）；综上所述：P点坐标为（2，2+1）或（2，﹣2+1）或（2，﹣）或（2，7）．2．（2022•岚山区一模）已知抛物线y＝ax2+bx+8与x轴交于A（﹣3，0），B（8，0）两点，交y轴于点C，点P是抛物线上一个动点，且点P的横坐标为m．（1）求抛物线的解析式；（2）如图2，将直线BC沿y轴向下平移5个单位，交x轴于点M，交y轴于点N．过点P作x轴的垂线，交直线MN于点D，是否存在一点P，使△BMD是等腰三角形？若存在，请直接写出符合条件的m的值；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+8与x轴交于A（﹣3，0），B（8，0）两点，∴，解得，，∴抛物线的解析式为y＝﹣x2+x+8；（3）易证线BC的解析式为y＝﹣x+8，向下平移5个单位得到y＝﹣x+3，当y＝0时，x＝3，∴M（3，0），当x＝0时，y＝3，∴N（0，3），由题意得PD⊥MB，∵MB＝8﹣3＝5，D（m，﹣m+3），∴MD2＝（m﹣3）2+（﹣m+3）2，BD2＝（8﹣m）2+（﹣m+3）2，若△BMD是等腰三角形，可分三种情况：①当MB＝MD时，∴（m﹣3）2+（﹣m+3）2＝25，解得m1＝3+，m2＝3﹣，②当MB＝BD时，∴（8﹣m）2+（﹣m+3）2＝25，解得，m1＝3（舍去），m2＝8（舍去），③当MD+BD时，∴（8﹣m）2+（﹣m+3）2＝（m﹣3）2+（﹣m+3）2，解得，m＝5.5．综上所述，m的值为3+或3﹣或5.5时，△BMD是等腰三角形．3．（2022•兴宁区校级模拟）如图，抛物线y＝﹣x2+bx+c过点A、B，抛物线的对称轴交x 轴于点D，直线y＝﹣x+3与x轴交于点B，与y轴交于点C，且．（1）求抛物线的解析式；（2）在x轴上是否存在点P，使得△PDC为等腰三角形？若存在，请求出点P的坐标，若不存在，请说明理由．【解答】解：（1）对于直线y＝﹣x+3，令y＝0，即﹣x+3＝0，解得：x＝3，令x＝0，得y＝3，∴B（3，0），C（0，3），∵A为x轴负半轴上一点，且OA＝OB，∴A（﹣1，0）．将点A、B的坐标分别代入y＝﹣x2+bx+c中，得，解得，∴抛物线的解析式为y＝﹣x2+2x+3；（3）存在．如图2，∵点P在x轴上，∴设P（m，0）．∵C（0，3），D（1，0），∴由勾股定理，得：CD2＝OC2+OD2＝32+12＝10，PD2＝（m﹣1）2，CP2＝OP2+OC2＝m2+32＝m2+9，分为三种情况讨论：①当CD＝PD时，CD2＝PD2，即10＝（m﹣1）2，解得m1＝1+，m2＝1﹣，此时点P的坐标为（1+，0）或（1﹣，0）；②当CD＝CP时，CD2＝CP2，即10＝m2+9，解得m1＝﹣1，m2＝1（不符合题意，舍去），此时点P的坐标为（﹣1，0）；③当PC＝PD时，PC2＝PD2，即m2+9＝（m﹣1）2，解得m＝﹣4，此时点P的坐标为（﹣4，0）．综上所述，在x轴上存在点P，使得△PDC为等腰三角形，满足条件的点P的坐标为（1+，0）或（1﹣，0）或（﹣1，0）或（﹣4，0）．4．（2022•鞍山模拟）抛物线与坐标轴交于A（﹣1，0）、B（4，0）、C（0，4），连接AC、BC．（1）求抛物线的解析式；（3）如图2，点E是抛物线上第一象限内对称轴右侧的一点，连接EC，点D是抛物线的对称轴上的一点，连接ED、CD，当△CED是以点E为顶点的等腰直角三角形时，直接写出点E的横坐标．【解答】解：（1）设抛物线的解析式为y＝ax2+bx+c，∵抛物线y＝ax2+bx+c过A（﹣1，0），B（4，0），C（0，4）三点，∴．解得：．∴抛物线对应的二次函数的解析式为y＝﹣x2+3x+4；（2）设G（x，﹣x2+3x+4），∵S△BHG＝S△ABG﹣S△ABH，S△AHC＝S△ABC﹣S△ABH，△BHG与△AHC的面积差为1，∵A（﹣1，0）、B（4，0），∴AB＝5，（3）∵y＝﹣x2+3x+4，∴抛物线对称轴为x＝﹣＝，，点E分别作EM⊥y轴于M，作EN⊥EM，过点D作DN⊥EN，垂足为N，∴∠CME＝∠DNE＝90°，∠MEN＝90°，∵△CED是以点E为顶点的等腰直角三角形，∴∠CED＝90°，∴∠CEM+∠MED＝∠DEN+∠MED＝90°，CE＝DE，∴∠CEM＝∠DEN，∴△EMC≌△END（AAS），∴CM＝DN，设E（m，﹣m2+3m+4）（m＞），∴4﹣（﹣m2+3m+4）＝m﹣，∴m＝或（不合题意，舍去），∴点E的横坐标为．5．（2022•渭滨区模拟）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q．（1）求抛物线的表达式；（2）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．【解答】解：（1）将A（﹣3，0），B（4，0）代入y＝ax2+bx+4，∴，解得，∴抛物线的表达式为：；（2）存在点Q，使得以A，C，Q为顶点的三角形是等腰三角形，理由如下：令x＝0，则y＝4，∴点C（0，4），∵A（﹣3，0）、C（0，4），∴AC＝5，设直线BC的解析式为y＝kx+b，∴，解得，∴y＝﹣x+4，设点M（m，0），则点Q（m，﹣m+4），①当AC＝CQ时，过点Q作QE⊥y轴于点E，连接AQ，∵CQ2＝CE2+EQ2，即m2+[4﹣（﹣m+4）]2＝25，解得：舍去负值），∴点；②当AC＝AQ时，则AQ＝AC＝5，在Rt△AMQ中，由勾股定理得：[m﹣（﹣3）]2+（﹣m+4）2＝25，解得：m＝1或m＝0（舍去0），∴点Q（1，3）；③当CQ＝AQ时，则2m2＝[m﹣（﹣3）]2+（﹣m+4）2，解得：舍去）；综上所述，点Q的坐标为（1，3）或．31。

《二次函数》专题训练（三）——抛物线的内接特殊三角形主备:鄢自红授课：鄢自红□自学导读【学习目标】（1）掌握二次函数图象内接特殊三角形的性质，并利用性质求解析式和参数的值。

（2）通过规律的推导和运用，提高类比推理和综合解题能力。

【重、难点】规律的推导和运用【读书思考】基础知识回顾:（1）抛物线顶点坐标公式:（_____, _________),简记为___________.（2）若抛物线与x轴有两个交点A(x1,0), B(x2,0)，AB=___________=________.（3）韦达定理：若ax2+bx+c=0(a≠0)有两实根x1,x2,则_________________________.□典题解析（一）抛物线与x轴两个交点和顶点确定的三角形例1.已知，二次函数y=x2+kx+1与x轴的两个交点A、B都在原点右侧，顶点为M。

当△ABM是等腰直角三角形时，（1）求k值。

（2）求判别式△.解析：先画出函数大致图象，再利用等腰三角形性质，结合直角三角形的性质求解。

问题1：例1中，如果把y=x2+kx+1换成y=ax2+bx+c，△ABM是等腰直角三角形时，△值不变吗？规律1：练习1（变式）. 已知抛物线y=x2—bx (b≠0)的顶点为M，与直线y=—2两交点分别为A、B，且△ABM为等腰直角三角形，则b=_______。

问题2：前面的问题中当△ABM为等边三角形时，y=ax2+bx+c的判别式△又是多少？导学设计教学重难点与抛物线内接特殊三角形有关的定值的推导和运用.教具准备多媒体．导学流程一、导入新课,揭示目标(2分钟) 情景导入：师生对照课件解读学习目标.二、新课导学基础知识回顾:（2分钟）（课件出示题目，点学生回答）自主探究完成例1（4分钟）（学生演板）追问拓展、合作探究：（3分钟）如果把y=x2+kx+1换成y=ax2+bx+c，△ABM是等腰直角三角形时，△还是4吗？规律小结（2分钟）：当y=ax2+bx+c(a≠0)与x轴交于A、B 两点，C是顶点，当△ABM为等腰直角三角形，则△=b2-4ac=4.练习1点拨：实质是把抛物线与y=0的交点变成了与y=-2的,但要注意△是方程x2-bx=-2的，而不是x2-bx=0的.自主探究问2（5分钟）1、先自主探究问题2，展示探究的结果.2、并利用探究的结论完成例2，利用例2检查学习效果。