(完整版)子系统与模块封装技术,S-函数编写-SIMULINK高级仿真
- 格式:doc
- 大小:374.01 KB
- 文档页数:15


Simulink仿真⼊门到精通(⼗)S函数10.1 S函数概述S函数也称为Simulink中的系统函数,是⽤来描述模块的Simulink宏函数,⽀持M、C等多种语⾔。
当Simulink默认的模块不能满⾜⽤户的需求时,⽤户可以通过S函数⾃⼰打造⼀个模块,实现⾃定义的算法或期待的动作。
10.2 S函数的类型S函数有多种类型,按照语⾔分类有M、C、C++、Fortran等编写的;按照所⽀持功能多少分类,包括Level1和Level2;按照执⾏⽅式分类,可分为直接解释运⾏的M S函数和编译为Mex⽂件后执⾏的C Mex S函数。
Level1 M S函数输⼊输出端⼝最多位1且数据维数固定,Level2 M S函数的输⼊输出端⼝个数可以为多个,数据维数也可以动态改变。
编写⼀个既能⽤于仿真⼜能⽤于代码⽣成的算法时,需要给S函数编写同名的TLC⽂件。
由于M语⾔需要调⽤MATLAB解释器,故C Mex S函数运⾏速度⽐M S函数更快。
10.3 S函数的要素⼀个Simulink模块包括输⼊、输出以及内部的状态量。
除了3要素之外,还有⼀个⽆处不在的时间量。
所谓状态量,根据系统性质分为连续系统中的微分量和离散系统中的差分量。
dx/dt=f(t,x,u)y=g(t,x,u)10.4 S函数的组成及执⾏顺序执⾏顺序:main{初始化模型;计算下⼀个采样时间点(⼤步长);while(未到达仿真终⽌时间){计算模块的输出;更新离散状态量;if(此模型带有连续状态模块){here:计算微分;计算模块的输出;if(精度未达标)goto here;过零检测;计算写⼀个采样时间点(⼤步长);}}执⾏仿真终⽌动作;}仿真运⾏时,模型⾸先要对模块进⾏初始化,这个过程包括模块的实例化:输⼊/输出端⼝、信号唯独、端⼝数据类型及采样时间等的确定,模块参数的获取及个数检查,并决定模块的执⾏顺序等。
实例化:Simulink标准库中提供的模块类似于C++等⾯向对象语⾔中的⼀个类,每当模块被拷贝或拖曳到模型中时,就相当于创建了这个类的⼀个对象,继承了这个类的属性并载⼊了默认的构造函数⽅法对其参数、端⼝等各个属性进⾏了初始化⼯作。

Simulink S-Function 编程(C语言)与模块封装技术1.S-Function概念S-Function(System function)是Simulink模块的计算机语言描述。
可以用M、C/C++、Ada、Fortran 语言以MEX(Matlab Executable,MATLAB可执行文件,在Windows系统中就是其为DLL)文件的形式编写。
S-Function以特殊的方式与Simulink方程求解器交互。
这种交互和Simulink内建模块的做法非常相似。
S-Function模块可以是连续、离散或者混合系统。
通过S-Function,用户可以将自己的模块加入Simulink模型中。
从而可以实现用户自定义的算法或者与硬件设备交互等。
2.S-Function工作机制2.1 Simulink模块的数学描述Simulink模块包括一系列输入、状态和输出。
输出是采样时间、输入、模块状态的函数。
下面的方程描述了输入、输出和状态的数学关系。
2.2 仿真过程Simulink模型的执行按下述几个步骤。
首先是初始化阶段。
在这一阶段Simulink将库模块集合到模型,传播宽度、数据类型和采样时间,评估模块参数,确定模块执行顺序,分配内存。
然后是仿真阶段。
此时Simulink进入一个仿真循环,循环的每次执行对应一个仿真步。
在每个仿真步,Simulink按初始化阶段确定的顺序执行各个模块。
对每个模块,Simulink计算模块在当前采样时间的状态、微分和输出。
这将持续到仿真结束。
图1描述了Simulink的仿真过程。
图1 Simulink执行仿真的步骤2.3 S-function的回调(Callback)方法S-function包括一系列的回调方法,用以执行每个仿真步骤所需的任务。
在一个模型的仿真过程中,每个仿真步骤,Simulink将调用各S-function的适当方法。
S-function执行的方法包括:●初始化:在首次仿真循环中执行。

《通信系统仿真》实验报告一、实验目的1、掌握S函数的结构和标准接口2、掌握S函数的编程方法3、掌握用S函数编写Simulink仿真模块的方法4、掌握S函数在Simulink仿真中的应用二、实验原理为了将系统数学方程与系统可视化模型联系起来,在Simulink中规定了固定的接口函数的形式,称为S函数,一切Simulink可视化模型都是基于S函数实现的。
系统可视化描述的直观性是以牺牲数学描述的简洁性为代价。
通过编写和使用S函数,用户也可以构建出采用Simulink的灵活性。
S函数可以用Matlab语言书写,也可以采用C++等语言编写。
S函数还可以进行编译,以提高执行速度。
Simulink内建的标准模块库就是用S函数编写并进行编译后形成的三、实验内容1、用S函数实现一个限幅器,当输入信号值小于设定的最小门限值时,输出为最小门限值;当输入信号值大于设定的最大门限值时,输出为最大门限值;如果信号值介于最小门限和最大门限之间,则直通。
写出限幅器的数学模型,对S函数实现的模块进行封装,要求能够在封装对话框中设置限幅的门限。
给出测试系统和测试仿真结果,并与Simulink基本库中的Saturation模块进行对比。
实验代码:function [sys,x0,str,ts]=xianSfun(t,x,u,flag,max,min)switch flag,case 0 %flag=0 初始化sizes= simsizes; %获取simulink仿真变量结构sizes.NumContStates = 0; %连续系统的状态数为0sizes.NumDiscStates = 0; %离散系统的状态数为0sizes.MumOutputs = 1; %输出信号数目是1sizes.MumInputs = 1; %输入信号数目是1sizes.DirFeedthrough = 1; %该系统是直通的sizes.NumSampleTimes = 1; %这里必须为1sys= simsizes(sizes);str = []; %通常为空矩阵x0 =[]; %初始状态矩阵x0ts =[0 0]; %采样时间有外部模块给出%限幅器函数--------------------------------------case 3 %flag=3 计算输出if u>maxsys=max;elseif u<minsys=min;elsesys=u;endcase {1,2,4,9} %其他不做处理的flag sys=[];otherwise %异常处理error(['Unhandled flag=',num2str(flag)]);end%主函数结束---------------------------------------仿真模型:运行结果:实验结论:限幅器的作用是限幅,输入幅度为2的余弦波,通过门限为0.5和-0.5的限幅器后,幅度大于0.5和幅度小于-0.5的部分都被限制了,即不能输出。





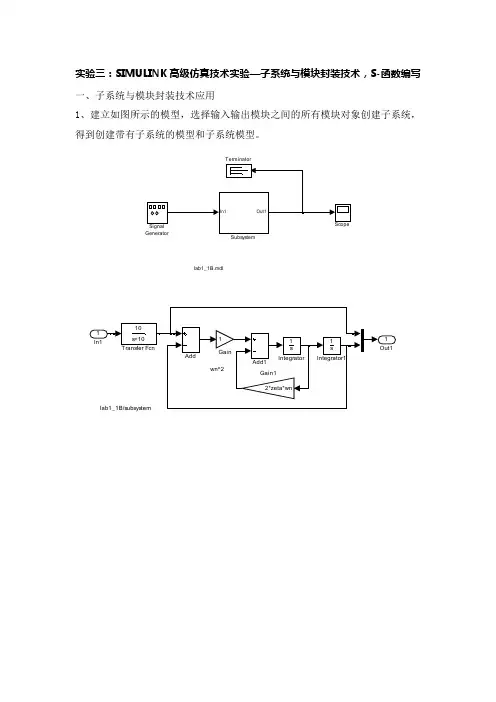
实验三:SIMULINK高级仿真技术实验—子系统与模块封装技术,S-函数编写一、子系统与模块封装技术应用1、建立如图所示的模型,选择输入输出模块之间的所有模块对象创建子系统,得到创建带有子系统的模型和子系统模型。
lab1_1B.mdl Terminator2、线性系统由下列微积分方程组成:1122231312322123535x x x x x x u x x x x u y x u u=-+⎧⎪=--+⎪⎨=---+⎪⎪=-+-⎩(1) 采用积分器方法在SIMULINK 上建立模型。
(2)对上述模型进行子系统封装,要求子系统的输入信号两个u1和u2,输出信号有四个x1,x2,x3和y 。
lab1_2B.mdl二、基于SIMULINK 的微分方程求解: 1、考虑下面给出的微分代数方程:11231222122321230.20.325210x x x x x x x x x x x x x x x =-++⎧⎪=--⎨⎪++-=⎩已知初始条件为123(0)0.8,(0)(0)0.1x x x ===。
在SIMULINK 上搭建微分代数方程的仿真模型,利用MATLAB 的函数模块进行编程,并对系统进行仿真。
-0.4-0.20.20.40.60.812、延迟微分方程的SIMULINK 求解。
考虑下面给出的延迟微分方程式:3()13()(1)0.2(0.5)(0.5)()3()2()4()x t x t y t x t x t y t y t y t x t =-------⎧⎨++=⎩要求:(1)建立延迟微分方程的SIMULINK 模型(2) 在阶跃输入下的系统状态变量和输出响应曲线,并在图上标注(),()x t y t 。
0123456789100.050.10.150.20.250.30.350.4tx &y三、双输入双输出系统的状态方程表示为:2.255 1.250.5462.25 4.25 1.250.25240.250.5 1.251221.25 1.750.250.75020001022x x u y x ---⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=+⎢⎥⎢⎥---⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤=⎢⎥⎣⎦输入信号分别是sin(),cos()t t ,要求:(1) 在SIMULINK 搭建上述多变量系统仿真模型,并利用MATLAB 语言绘制系统的输出曲线和状态曲线。
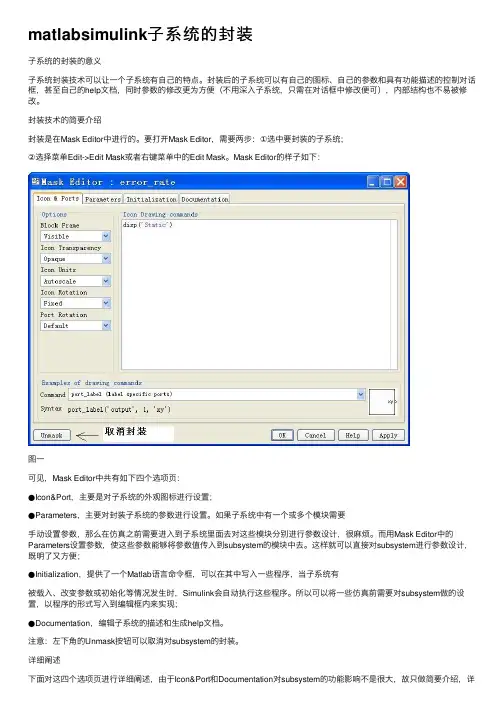
matlabsimulink⼦系统的封装⼦系统的封装的意义⼦系统封装技术可以让⼀个⼦系统有⾃⼰的特点。
封装后的⼦系统可以有⾃⼰的图标、⾃⼰的参数和具有功能描述的控制对话框,甚⾄⾃⼰的help⽂档,同时参数的修改更为⽅便(不⽤深⼊⼦系统,只需在对话框中修改便可),内部结构也不易被修改。
封装技术的简要介绍封装是在Mask Editor中进⾏的。
要打开Mask Editor,需要两步:①选中要封装的⼦系统;②选择菜单Edit->Edit Mask或者右键菜单中的Edit Mask。
Mask Editor的样⼦如下:图⼀可见,Mask Editor中共有如下四个选项页:●Icon&Port,主要是对⼦系统的外观图标进⾏设置;●Parameters,主要对封装⼦系统的参数进⾏设置。
如果⼦系统中有⼀个或多个模块需要⼿动设置参数,那么在仿真之前需要进⼊到⼦系统⾥⾯去对这些模块分别进⾏参数设计,很⿇烦。
⽽⽤Mask Editor中的Parameters设置参数,使这些参数能够将参数值传⼊到subsystem的模块中去。
这样就可以直接对subsystem进⾏参数设计,既明了⼜⽅便;●Initialization,提供了⼀个Matlab语⾔命令框,可以在其中写⼊⼀些程序,当⼦系统有被载⼊、改变参数或初始化等情况发⽣时,Simulink会⾃动执⾏这些程序。
所以可以将⼀些仿真前需要对subsystem做的设置,以程序的形式写⼊到编辑框内来实现;●Documentation,编辑⼦系统的描述和⽣成help⽂档。
注意:左下⾓的Unmask按钮可以取消对subsystem的封装。
详细阐述下⾯对这四个选项页进⾏详细阐述,由于Icon&Port和Documentation对subsystem的功能影响不是很⼤,故只做简要介绍,详细内容参考help⽂档。
Icon&port如图⼀所⽰,该选项页有三部分:Options、Icon Drawing Commands和Examples of drawing commands。
实验三:SIMULINK高级仿真技术实验—子系统与模块封装技术,S-函数编写
一、子系统与模块封装技术应用
1、建立如图所示的模型,选择输入输出模块之间的所有模块对象创建子系统,得到创建带有子系统的模型和子系统模型。
lab1_1B.mdl Terminator
2、线性系统由下列微积分方程组成:
1
1
2
2
2
3
1
3
1
2
3
2
2
1
2
3535x x x x
x x u x x x x u y x u u
=-+⎧
⎪=--+⎪⎨
=---+⎪⎪=-+-⎩&&&
(1) 采用积分器方法在SIMULINK 上建立模型。
(2)对上述模型进行子系统封装,要求子系统的输入信号两个u1和u2,输出信号有四个x1,x2,x3和y 。
lab1_2B.mdl
二、基于SIMULINK 的微分方程求解: 1、考虑下面给出的微分代数方程:
1
1
2
3
12
2
2
1
2
2
3
2
1
2
3
0.20.325210x x x x x x x x x x x x x x x =-++⎧⎪
=--⎨⎪++-=⎩
&&
已知初始条件为12
3
(0)
0.8,(0)(0)0.1x x x ===。
在SIMULINK 上搭建微分代数方程的仿真模型,利用MATLAB 的函数模块进行编程,并对系统进行仿真。
-0.4
-0.2
0.2
0.4
0.6
0.8
1
2、延迟微分方程的SIMULINK 求解。
考虑下面给出的延迟微分方程式:
3
()13()(1)0.2(0.5)(0.5)()3()2()4()x t x t y t x t x t y t y t y t x t =-------⎧⎨
++=⎩
&&&& 要求:(1)建立延迟微分方程的SIMULINK 模型
(2) 在阶跃输入下的系统状态变量和输出响应曲线,并在图上标注
(),()x t y t 。
01234
5678910
0.050.10.150.20.25
0.30.350.4t
x &y
三、双输入双输出系统的状态方程表示为:
2.255 1.250.54
62.25 4.25 1.250.25240.250.5 1.251221.25 1.750.25
0.750200010
2
2x x u y x ---⎡⎤⎡⎤
⎢⎥
⎢⎥---⎢
⎥⎢
⎥=+⎢⎥⎢⎥---⎢
⎥⎢
⎥---⎣⎦⎣⎦
⎡⎤
=⎢
⎥⎣⎦
& 输入信号分别是sin(),cos()t t ,要求:
(1) 在SIMULINK 搭建上述多变量系统仿真模型,并利用MATLAB 语言绘制
系统的输出曲线和状态曲线。
lab3_1mdl+initialab3.m+plotlab4.m
State
t
x
01234
5678910
-4
-3-2-1
Out
t
y
(2)在SIMULINK 上搭建如图所示的仿真模型,用MATLAB 语言编写S-函数(lab4sf12),绘制系统的输出曲线和状态曲线。
lab3_2.mdl+lab3sf.m+plotlab4.m
四、利用S-函数设计跟踪微分器,跟踪微分器是为了减少噪声放大效应提出的,根据功能划分为两个环节即:
2
1
2
2
2
(),()2r
w s w s s s rs r
==++
其中1()w s 的阶跃响应保证无超调达到设定值,并随r 的增大加快到达设定值。
整个跟踪微分器为1
2
()
()()w s w s w s =g ,写成状态空间的形式为:
1
2
2
2
1
2
()2v v v
r u v r v =⎧⎨
=--⎩&&g
要求:
(1) 在SIMULINK 上建立下列的跟踪微分器仿真模型。
(2)编写M文件的S函数——active_control_lab4sf22。
先把
12
2
212
()2
v v
v r u v r v
=
⎧
⎨
=--
⎩
&
&g写成状态方程形式。
r=60
r=120
r=10
五、基于SIMULINK 的动态系统仿真应用:某控制系统的传递函数为:
要求:(1)在SIMULINK 上建立仿真模型
(2)用示波器观察记录下单位阶跃信号下响应曲线
lab331.mdl
s+30s +23s
2Transfer Fcn
Step
Scope
2
()()30
,()()1()23Y s G s s G s X s G s s s
+==++。