一次函数基础训练题(后附答案)

一次函数基础训练题一、一次函数的定义与表达式1. 题目下列函数中，是一次函数的是（）A. y = (1)/(x)+1B. y = x^2+1C. y = 2x 1D. y=√(x)+1解析一次函数的一般形式为y = kx + b（k，b为常数，k≠0）。

选项A，y=(1)/(x)+1是反比例函数与常数函数的和，不是一次函数，因为反比例函数y = (1)/(x)不符合一次函数形式。

选项B，y = x^2+1是二次函数，因为自变量x的次数是2，不符合一次函数自变量次数为1的要求。

选项C，y = 2x 1符合一次函数y = kx + b的形式，其中k = 2，b=-1。

选项D，y=√(x)+1，自变量x在根号下，不是一次函数。

所以答案是C。

2. 题目已知一次函数y=(m 1)x+3，求m的取值范围。

解析因为一次函数的一般形式为y = kx + b（k≠0），在函数y=(m 1)x+3中，k = m 1。

要使函数为一次函数，则m 1≠0，解得m≠1。

二、一次函数的图象与性质1. 题目一次函数y = 2x+1的图象经过哪几个象限？解析对于一次函数y = kx + b（k，b为常数，k≠0），当k>0，b>0时，图象经过一、二、三象限。

在函数y = 2x+1中，k = 2>0，b = 1>0，所以图象经过一、二、三象限。

2. 题目已知一次函数y=-3x + b的图象经过点(1, -1)，求b的值，并判断函数图象的单调性。

解析因为函数y=-3x + b的图象经过点(1,-1)，将x = 1，y=-1代入函数可得：-1=-3×1 + b-1=-3 + b移项可得b=-1 + 3=2。

对于一次函数y = kx + b，这里k=-3<0，所以函数y=-3x + 2的图象是单调递减的，即y随x的增大而减小。

三、一次函数的应用1. 题目某汽车油箱中原有油100升，汽车每行驶50千米耗油9升，求油箱剩余油量y（升）与汽车行驶路程x（千米）之间的函数关系式。

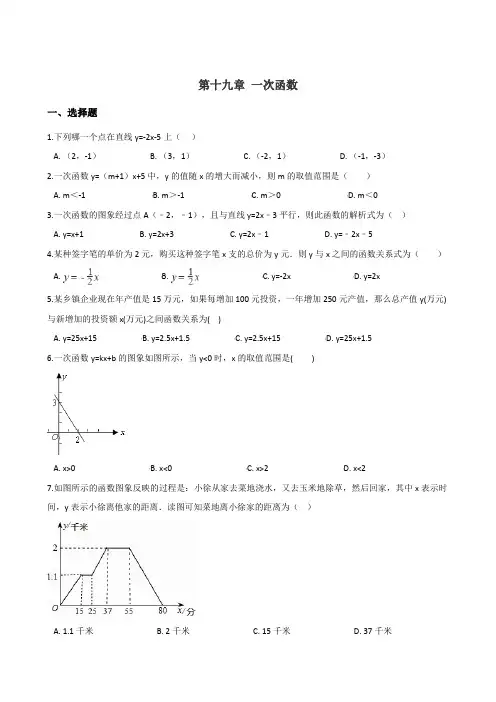
第十九章一次函数一、选择题1.下列哪一个点在直线y=-2x-5上（）A. （2，-1）B. （3，1）C. （-2，1）D. （-1，-3）2.一次函数y=（m+1）x+5中，y的值随x的增大而减小，则m的取值范围是（）A. m＜-1B. m＞-1C. m＞0D. m＜03.一次函数的图象经过点A（﹣2，﹣1），且与直线y=2x﹣3平行，则此函数的解析式为（）A. y=x+1B. y=2x+3C. y=2x﹣1D. y=﹣2x﹣54.某种签字笔的单价为2元，购买这种签字笔x支的总价为y元．则y与x之间的函数关系式为（）A. B. C. y=-2x D. y=2x5.某乡镇企业现在年产值是15万元，如果每增加100元投资，一年增加250元产值，那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为( )A. y=25x+15B. y=2.5x+1.5C. y=2.5x+15D. y=25x+1.56.一次函数y=kx+b的图象如图所示，当y<0时，x的取值范围是( )A. x>0B. x<0C. x>2D. x<27.如图所示的函数图象反映的过程是：小徐从家去菜地浇水，又去玉米地除草，然后回家，其中x表示时间，y表示小徐离他家的距离．读图可知菜地离小徐家的距离为（）A. 1.1千米B. 2千米C. 15千米D. 37千米8.如图，在平面直角坐标系中，直线l1：y=x+3与直线l2：y=mx+n交于点A（﹣1，b），则关于x、y的方程组的解为（）A. B. C. D.9.一次函数y=kx+b的图象如图所示，则不等式kx+b＜0的解集是（）A. x＞﹣2B. x＜﹣2C. x＞﹣4D. x＜﹣410.小明到离家900米的春晖超市卖水果，从家中到超市走了20分钟，在超市购物用了10分钟，然后用15分钟返回家中，下列图形中表示小明离家的时间与距离之间的关系是（）A. B. C. D.11.一次函数y=x+5的图象经过点P(a，b)和Q(c，d)，则a(c－d)－b(c－d)的值为（）A. 9B. 16C. 25D. 3612.一次函数y=kx+b（k，b是常数，k≠0）的图象，如图所示，则不等式kx+b＞0的解集是（）A. x＜2B. x＜0C. x＞0D. x＞2二、填空题13.函数y=中，自变量x的取值范围为________ ．14.已知，函数y=（k﹣1）x+k2﹣1，当k________ 时，它是一次函数．15.当x=-1时，一次函数y=kx+3的值为5，则k的值为________ ．16.已知长方形的周长为30cm，一边长为ycm，另一边长为xcm，则y与x的关系式为________，其中变量是________，常量是________．17.根据如图所示的计算程序计算变量y的对应值，若输入变量x的值为- ，则输出的结果为 ________18.某书定价25元，如果一次购买20本以上，超过20本的部分打八折，试写出付款金额y（单位：元）与购书数量x（单位：本）之间的函数关系________．19.已知A地在B地的正南方3km处，甲、乙两人同时分别从A、B两地向正北方向匀速直行，他们与A 地的距离S（km）与所行时间t(h)之间的函数关系如图所示，当他们行驶3h时，他们之间的距离为________km.20.如图，已知点A和点B是直线y=x上的两点，A点坐标是（2，）．若AB=5，则点B的坐标是 ________．21.一次函数y=ax+b的图象如图，则关于x的不等式ax+b≥0的解集为________．22.某水库的水位在5小时内持续上涨，初始水位高度为6米，水位以每小时0.3米的速度匀速上升，则水库的水位高度y（米）与时间x（小时）（0≤x≤5）的函数关系式为________ ．三、解答题23.一次函数y＝kx＋b经过点(－4，－2)和点(2，4)，求一次函数y＝kx＋b的解析式。

5.3 一次函数(一)1．下列y 关于x 的函数中，是一次函数的是(B )A. y ＝1－xB. y ＝15x ＋1C. y ＝x 2＋1D. y ＝x2．若y ＝(m －3)x ＋1是一次函数，则(C )A. m ＝3B. m ＝－3C. m ≠3D. m ≠－33．(1)在一次函数y ＝5－13x 中，系数k ＝－13，b ＝__5__． (2)已知y 与x 成正比例，且当x ＝－2时，y ＝4，则y 与x 之间的函数表达式是y ＝－2x ．(3)已知函数y ＝(3m －4)x n －2＋(m ＋2n )是正比例函数，则m ＝－6，n ＝__3__，此时函数表达式为y ＝－22x ．4．已知函数y ＝3x ＋1，当自变量增加3时，相应的函数值增加多少？【解】 由y ＝3x ＋1，y ＋a ＝3(x ＋3)＋1，两式相减，得a ＝9.∴相应的函数值增加9.5．请说出下列函数中k 和b 的值：(1)y ＝60x .(2)y ＝3000－300x .(3)y ＝9＋8x .(4)y ＝－3(2＋x )－7.【解】 (1)k ＝60，b ＝0.(2)k ＝－300，b ＝3000.(3)k ＝8，b ＝9.(4)代简，得y ＝－3x －13，∴k ＝－3，b ＝－13.6．已知y －3与x 成正比例，且当x ＝2时，y ＝7.(1)求y 与x 之间的函数表达式．(2)当x ＝－2时，求y 的值．(3)当y ＝－3时，求x 的值．【解】 (1)设y －3＝kx .∵当x ＝2时，y ＝7，∴7－3＝2k ，∴k ＝2.∴y ＝2x ＋3.(2)当x ＝－2时，y ＝－2×2＋3＝－1.(3)当y ＝－3时，－3＝2x ＋3，∴x ＝－3.7．定义[a ，b ]为一次函数y ＝ax ＋b (a ≠0，a ，b 为实数)的“关联数”．若“关联数”为[1，m －3]的一次函数是正比例函数，则关于x 的方程mx －6＝0的解为多少？【解】 ∵“关联数”为[1，m －3]的一次函数是正比例函数，∴y ＝x ＋m －3是正比例函数，即m －3＝0，解得m ＝3.把m ＝3代入mx －6＝0，得3x －6＝0，解得x ＝2.8．写出下列各小题中y 关于x 的函数表达式，并判断y 是否为x 的一次函数？是否为x 的正比例函数？(1)长方形的面积为20，长方形的长y 与宽x 之间的函数表达式．(2)某地西瓜刚上市时的价格为3.6元/千克，买西瓜的总价y (元)与所买西瓜x (kg)之间的函数表达式．(3)地面气温为28 ℃，高度每升高1 km ，气温下降5 ℃，气温y (℃)与高度x (km )之间的函数表达式．(4)小林的爸爸为小林存了一份教育储蓄，首次存入10000元，以后每个月存入500元，存入总钱数y (元)与月数x 之间的函数表达式．【解】 (1)y ＝20x，不是一次函数，也不是正比例函数． (2)y ＝3.6x ，是一次函数，也是正比例函数．(3)y ＝28－5x ，是一次函数，但不是正比例函数．(4)y ＝10000＋500x ，是一次函数，但不是正比例函数．9．某市住宅电话的资费标准为：通话前3 min 计费0.20元，以后每分钟(不足1 min 按1 min 计算)加收0.10元．(1)某人一次通话的时间为10 min ，他这次通话的资费是0.90元．(2)某人一次通话的资费为1.50元，他这一次的通话时间t 的范围是15__min<t ≤16__min ．【解】 (1)当通话时间为10 min 时，通话前3 min 收费0.20元，后7 min 收费7×0.10＝0.70(元)，∴总资费为0.20＋0.70＝0.90(元)．(2)当一次通话的资费为1.50元时，此人通话时间最多为3＋(1.50－0.20)÷0.10＝16(min)， ∴通话时间t 应满足15 min<t ≤16 min.10．(1)已知一次函数y ＝kx ＋b ，当x 的值减少1时，y 的值减少2，则当x 的值增加2时，y 的值(A )A. 增加4B. 减少4C. 增加2D. 减少2【解】 由y ＝kx ＋b ，y －2＝k (x －1)＋b ，两式相减，得k ＝2.由y ＝2x ＋b ，y ＋a ＝2(x ＋2)＋b ，两式相减，得a ＝4，∴y 的值增加4.(2)设m ，n (m ≠0)为常数，如果在正比例函数y ＝kx 中，自变量x 增加m ，对应的函数值y 增加n ，那么k 的值是(A )A. n mB. m nC. －n mD. －m n【解】 由题意，得⎩⎪⎨⎪⎧y ＝kx ，①y ＋n ＝k （x ＋m ），②②－①，得n ＝km ，解得k ＝n m.11．若函数y ＝(2k －5)x ＋(k －25)为正比例函数，求12＋16＋112＋…＋1k ＋k 2的值． 【解】 ∵函数y ＝(2k －5)x ＋(k －25)为正比例函数，∴k －25＝0，解得k ＝25.∵1k ＋k 2＝1k （k ＋1）＝1k －1k ＋1， ∴12＋16＋112＋…＋1k ＋k 2＝1－12＋12－13＋13－14＋125－126＝1－126＝2526.(第12题)12．某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物，装卸货物共用45 min ，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60 km /h ，两车之间的距离y (km )与货车行驶时间x (h )之间的函数图象如图所示，有下列结论：①快递车从甲地到乙地的速度为100 km /h ；②甲、乙两地之间的距离为120 km ；③图中点B 的坐标为(3.75，75)；④快递车从乙地返回时的速度为90 km /h .其中正确的是(C )A. ①②③B. ②③④C. ①③④D. ①③【解】 根据题意可得：点A 表示快递车已到达乙地，y 表示两车距离，3 h 时两车相距120 km .设快递车从甲地到乙地的速度为a(km/h)，则有3a－3×60＝120，解得a＝100，故①正确．两地距离为3×100＝300(km)，故②错误．∵快递车到达后装卸货物共用时45 min，即34h，∴点B的横坐标x＝3.75.＝45(km)，∵45 min货车走了60×34∴点B的纵坐标为120－45＝75，故③正确．BC段中的点B表示快递车装好货后又出发，点C表示两车相遇．∵4.25－3.75＝0.5(h)，即两车经过0.5 h相遇，∴快递车返回的速度为(75－0.5×60)÷0.5＝90(km/h)，故④正确．综上所述，①③④正确．。

一次函数练习题(附答案)篇一：一次函数测试题及其答案一次函数测试题1. 函数y=中，自变量x的取值范围是（） x?1A．x≥0 B．x>1 C．x>0且x≠1 D．x≥0且x≠1 2. 已知正比例函数y=-2x，当x=-1时，函数y的值是（）A．2 B．-2 C．-0.5 D．0.5 3. 一次函数y=-2x-3的图像不经过（）A．第一象限 B．第二象限 C．第三象限 D．第四象限4. 某校八年级同学到距学校6千米的郊外秋游，一部分同学步行，另一部分同学骑自行车，沿相同路线前往，如图，L1L2分别表示步行和骑车的同学前往目的地所走的路程y（千米）与所用时间x （分钟）之间的函数关系，则以下判断错误的是（） A．骑车的同学比步行的同学晚出发30分钟 B．骑车的同学和步行的同学同时到达目的地C．骑车的同学从出发到追上步行的同学用了20分钟 D．步行的速度是6千米/小时。

5. 已知一次函数y=（m+2）x+（1-m），若y随x的增大而减小，且此函数图像与y轴的交点在x轴上方，则m的取值范围是（）A．m>-2 B．m<1 C．<-2 D．-2<m<16. （2021福建福州）已知一次函数y?(a?1)x?b的图象如图所示，那么a的取值范围是（）A．a?1 B．a?1C．a?0D．a?07. （2021上海市）如果一次函数y?kx?b的图象经过第一象限，且与y轴负半轴相交，那么（） A．k?0，b?0B．k?0，b?0C．k?0，b?0D．k?0，b?08. （2021陕西）如图，一次函数图象经过点A，且与正比例函数图象交于点B，则该一次函数的表达式为（） A．y??x?2C．y?x?2B．y?x?2 D．y??x?2）9. （2021浙江湖州）将直线y＝2x向右平移2个单位所得的直线的解析式是（。

CA、y＝2x＋2B、y＝2x－2C、y＝2(x－2)D、y＝2(x＋2) 10. 已知两点M（3，5），N（1，-1），点P是x轴上一动点，若使PM+PN最短，则点P的坐标点是（）A．（0，-4）B．（2，0） 3C．（4，0） 3D．（3，0） 2二、填空题 11. 若点A（2，，-4）在正比例函数y=kx的图像上，则k=_____。

一次函数（基础篇）专项练习1一、单选题1．下列图象中，表示y 是x 的函数的是（）A ．B ．C ．D ．2．在函数1y =x 的取值范围是（）A ．2x >B ．2x ≠C ．2x <D ．2x ≤3．一次函数y ＝（k ﹣1）x +3的图象经过点（﹣2，1），则k 的值是（）A ．﹣1B ．2C ．1D ．04．一次函数y=kx+b 的图像经过点（-1，2），则k-b 的值是（）A ．-1B ．2C ．1D ．-25．一次函数y ＝12x ﹣m 的图象上有两点A （﹣2，y 1），B （3，y 2），则y 1，y 2的大小关系为（）A ．y 1＞y 2B ．y 1＝y 2C ．y 1＜y 2D ．无法确定6．如图是一次函数112y x =-的图象，根据图象可直接写出方程1102x -=的解为2x =，这种解题方法体现的数学思想是（）A ．数形结合思想B ．转化思想C ．分类讨论思想D ．函数思想7．一根蜡烛长30cm ，点燃后每小时燃烧5cm ，燃烧时蜡烛剩余的长度h （cm ）和燃烧时间t （小时）之间的函数关系用图像可以表示为中的（）A ．B ．C ．D ．8．已知一次函数y ＝﹣2x ＋4，下列说法错误的是（）A ．图象经过第一、二、四象限B ．图象与x 轴的交点坐标为（4，0）C ．y 随x 增大而减小D ．该图象可以由y ＝﹣2x 平移得到9．若关于x 的不等式组2−>0−2≤0有且只有四个整数解，且一次函数y =（k +3）x +k +5的图象不经过第三象限，则符合题意的整数k 有（）个．A ．4B ．3C ．2D ．110．如图，在平面直角坐标系中，直线1l ：152y x =-+与x 轴、y 轴分别交于点A 和点B ，直线2l 经过坐标原点，且21l l ⊥，垂足为C ，则点C 到y 轴的距离为（）A ．1B ．2C ．3D ．4二、填空题11．已知f （x ）＝22x x-，那么f （2）＝_____．12．如图，在平面直角坐标系中，点A （2，m ）在第一象限，若点A 关于x 轴的对称点B 在直线y ＝﹣x+1上，则m 的值为_____．13．若y=（m ﹣1）x |m|是正比例函数，则m 的值为_____.14．直线2y x b =+（b 为常数）的图象经过第一、三、四象限，则b 的值可以是______（写出一个即可）．15．已知正比例函数的图象经过点M （﹣2，1）、A （x 1，y 1）、B （x 2，y 2），如果x 1＜x 2，那么y 1_____y 2．（填“＞”、“＝”、“＜”）16．已知一次函数(1)2(1)y m x m m =++-≠-，将该函数图象先向下平移2个单位长度，再向右平移4个单位长度，平移后的函数图象过点(1,2)-，则m 的值为___________．17．已知在正比例函数y ＝－2mx 中，函数y 的值随x 值的增大而增大，则点P （m ，4）在第______象限．18．若A(x 1，y 1)、B(x 2，y 2)是一次函数2y ax x =+-图像上的不同的两点，记()()1212m x x y y =--，则当m ＜0时，a 的取值范围是___．19．一次函数y =2x +4的图象与x 轴、y 轴的交点分别为A ，B ，则线段AB 的长为_____________．20．已知一次函数21y x =-+，若21x -≤≤，则y 的最小值为_________________．21．一次函数2y kx k =+的图象如图所示，当0y >时，则x 的取值范围是_______．22．如图，直线y =，点1A 坐标为()1,0，过点1A 作x 轴的垂线交直线于点1B ，以原点O 为圆心，1OB 长为半径画弧交x 轴于点2A ；再过点2A 作x 轴的垂线交直线于点2B ，以原点O 为圆心，2OB 长为半径画弧交x 轴于点3A ，…，按此做法进行下去，点2021B 的坐标为______．三、解答题23．已知一次函数y ＝kx ＋b 的图象经过点A (―1，3)和点B (2，―3)．(1)求这个一次函数的表达式；(2)求直线AB 与坐标轴围成的三角形的面积．24．有一个容量为8GB（1GB＝1024MB）的U盘，U盘中已经存储了1个视频文件，其余空间都用来存储照片．若每张照片占用的内存容量均相同，照片数量x（张）和剩余可用空间y（MB）的部分关系如表：照片数量100150200400800剩余可用空间56005400520044002800（1）求出y与x之间的关系式．（2）若U盘中已经存入1100张照片，那么最多还能存入多少张照片？25．如图，直线l1经过点A（0，2）和C（6，﹣2），点B的坐标为（4，2），点P是线段AB上的动点（点P不与点A重合），直线l2：y＝kx+2k（k≠0）经过点P，并与l1交于点M．（1）求l1的函数表达式；（2）若点M坐标为（1，43），求S△APM；（3）无论k取何值，直线l2恒经过点，在P的移动过程中，k的取值范围是．26．某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，问：（1）求一次函数解析式（2）旅客可携带的免费行李的最大质量是多少kg？27．直线24y x =-+与x 轴交于点A ，与y 轴交于点B ，直线(y kx b k b =+，是常数，0)k ≠经过点A ，与y 轴交于点C ，且OC OA =．()1求点A 的坐标及k 的值；()2点C 在x 轴的上方，点P 在直线24y x =-+上，若PC PB =，求点P 的坐标．28．如图，已知函数12y x b =-+的图象与x 轴、y 轴分别交于点A ，B ，与函数y ＝x 的图象交于点M ，点M 的横坐标为2．在x 轴上有一点P (a ，0)（其中a>2），过点P 作x 轴的垂线，分别交函数12y x b =-+和y ＝x 的图象于点C ，D（1）求点A 的坐标；（2）若OB ＝CD ，求a 的值．参考答案1．A【分析】根据函数的定义可知，满足对于x 的每一个取值，y 都有唯一确定的值与之对应关系，据此即可确定函数的个数．解：A 、对于x 的每一个取值，y 都有唯一确定的值与之对应，故A 正确；B 、对于x 的每一个取值，y 可能有三个值与之对应，故B 错误；C 、对于x 的每一个取值，y 可能有两个值与之对应，故C 错误；D 、对于x 的每一个取值，y 可能有两个值与之对应，故D 错误；故选：A ．【点拨】主要考查了函数的定义，在一个变化过程中有两个变量x ，y ，对于x 的每一个取值，y 都有唯一确定的值与之对应，则y 是x 的函数，x 叫自变量．2．D【分析】根据二次根式的意义，被开方数大于等于0，列不等式求解即可得出结论．解：由题意得：2-x ≥0，解得x ≤2．故选：D ．【点拨】本题主要考查了求自变量的取值范围，掌握二次根式的被开方数是非负数是解题的关键．3．B【分析】函数经过点（﹣2，1），把点的坐标代入解析式，即可求得k 的值．解：根据题意得：﹣2（k ﹣1）+3＝，解得：k ＝2．故选B ．【点拨】本题主要考查了函数的解析式与图象的关系，满足解析式的点一定在图象上，图象上的点一定满足函数解析式．4．D【分析】根据一次函数的性质即可得．解：由题意，将点(1,2)-代入一次函数的解析式得2k b -+=则2k b -=-故选：D ．【点拨】本题考查了一次函数的性质，掌握理解一次函数的性质是解题关键．5．C【分析】直接根据一次函数的增减性判断即可．解：∵一次函数y ＝12x ﹣m 中，k ＝12＞0，∴y 随x 的增大而增大．∵﹣2＜3，∴y 1＜y 2．故选：C ．【点拨】本题主要考查一次函数的性质，熟练掌握函数性质是解题的关键．6．A【分析】根据图像与x 轴交点可得方程的解，体现的是数形结合的思想．解：由图像可知y =0时，与x 轴交于(2,0)点，故1102x -=的解为2x =，这种解题方法体现的是数形结合的数学思想．【点拨】本题主要考查根据函数图像求方程的解，正确理解函数图像各点的含义是解题关键．7．B【分析】根据蜡烛剩余的长度=总长度-燃烧的长度就可以得出函数的解析式，由题意求出自变量的取值范围就可以得出函数图象．解：由题意，得y=30-5t ，∵y≥0，t≥0，∴30-5t≥0，∴t≤6，∴0≤t≤6，∴y=30-5t 是降函数且图象是一条线段．故选B ．【点拨】本题考查一次函数的解析式的运用，一次函数的与实际问题的关系的运用，一次函数的图象的运用，自变量的取值范围的运用，解答时求出函数解析式及自变量的范围是关键．8．B【分析】根据一次函数的解析式中一次项系数20k =-<，40b =>，即可判断经过的象限进而判断A 选项，令0y =即可判断B 选项，根据一次项系数20k =-<，即可判断C 选项，根据一次函数平移的规律可判断D 选项．解：由24y x =-+，20k =-<，40b =>，∴一次函数24y x =-+图象经过第一、二、四象限，故A 选项正确，不符合题意；令0y =，则2x =，∴图象与x 轴的交点坐标为(2,0)故B 选项不正确，符合题意；20k =-<，∴y 随x 增大而减小；故C 选项正确，不符合题意；将一次函数2y x =-图象向上平移4个单位可得24y x =-+，故D 选项正确，不符合题意．故选B【点拨】本题考查了一次函数图象与性质，一次函数图象的平移，一次函数与坐标轴的交点，掌握一次函数的图象与性质是解题的关键．9．D 【解析】试题分析：解不等式组2−>0−2≤0得，2＜x≤2，∵不等式组有且只有四个整数解，∴其整数解为：﹣1，0，1，2，∴﹣2≤2＜﹣1，即﹣4≤k ＜﹣2．∵一次函数y=（k+3）x+k+5的图象不经过第三象限，∴+3<0k +5≥0，解得﹣5≤k ＜﹣3，∴﹣4≤k ＜﹣3，∴k 的整数解只有﹣4．故选D ．【考点】一次函数与一元一次不等式．10．B【分析】先分别求得A ，B 两点坐标，然后利用勾股定理求得AB 的长，结合三角形面积求得OC 的长，再利用勾股定理求得BC ，最后再利用三角形面积求解解：在152y x =-+中，当x =0时，y =5当y =0时，15=02x -+，解得：x =10∴OA =10；OB =5∴在Rt △AOB 中，AB =∵21l l ⊥∴1122AB OC OA OB ⋅=⋅，1151022⨯=⨯⨯，解得：OC =∴在Rt △BOC 中，BC ==过点C 作CD ⊥y 轴∴1122OB CD BC ⋅=⋅，11522CD ⨯=⨯2CD =故选：B【点拨】本题考查一次函数的几何应用及勾股定理解直角三角形，二次根式的乘除运算，利用数形结合思想解题是关键．11．1【分析】把x=2代人f （x ）=22x x-，求得答案即可．解：当x ＝2时，f （2）＝2222-＝1，故答案为：1．【点拨】考查了函数值的知识，解题的关键是代人后正确的计算，难度不大．12．1【分析】根据关于x 轴的对称点的坐标特点可得B （2，−m ），然后再把B 点坐标代入y ＝−x ＋1可得m 的值．解：点A 关于x 轴的对称点B 的坐标为：（2，﹣m ），将点B 的坐标代入直线y ＝﹣x+1得：﹣m ＝﹣2+1，解得：m ＝1，故答案为1．【点拨】此题主要考查了关于x 轴对称点的坐标，以及一次函数图象上点的坐标特点，关键是掌握凡是函数图象经过的点必能使解析式左右相等．13．-1【分析】根据正比例函数的定义，令m-1≠0，|m|=1即可．解：由题意得：m−1≠0，|m|=1，解得：m=−1.故答案为−1.【点拨】本题考查正比例函数的定义.14．-1（答案不唯一，b ＜0即可）【分析】由一次函数图象经过第一、三、四象限，可知k ＞0，b ＜0，在范围内确定b 的值即可．解：因为一次函数2y x b =+（b 为常数）的图象经过第一、三、四象限，所以k ＞0，b ＜0，所以b 可以取-1，故答案为：-1（答案不唯一，b ＜0即可）【点拨】此题考查一次函数图象与系数的关系，根据一次函数图象所经过的象限，可确定一次项系数，常数项的值的符号，从而确定字母k 的取值范围．15．>【分析】根据正比例函数的性质，解答即可．解：设该正比例函数的解析式为y ＝kx ，则1＝﹣2k ，得k ＝﹣0.5，∴y ＝﹣0.5x ，∵正比例函数的图象经过点A （x 1，y 1）、B （x 2，y 2），x 1＜x 2，∴y 1＞y 2，故答案为：＞．【点拨】本题考查了正比例函数的性质，掌握性质是解题的关键．16．52-【分析】根据函数图象平移的规律：“上加下减”“左加右减”的原则即可求得．解：由题意得一次函数y=(m+1)（x-4）+m−2-2(m≠−1)经过点（1，-2）∴(m+1)（1-4）+m−2-2=-2，解得：m=-52，故答案为：-52．【点拨】本题考查一次函数的图象与几何变换，熟知平移的原则是解题的关键．17．二【分析】根据正比例函数y 的值随x 值的增大而增大，可知20m ->，求得0m <，即可判断P （m ，4）在第二象限．解：∵函数y 的值随x 值的增大而增大，∴20m ->，解得0m <，∴点P （m ，4）在第二象限．【点拨】本题考查正比例函数，较容易，熟练掌握正比例函数的性质是顺利解题的关键．18．1a <-【分析】根据一次函数的性质知，当k ＜0时，判断出y 随x 的增大而减小．解：∵A(1x ，1y )、B(2x ，2y )是一次函数()212y ax x a x =+-=+-图象上的不同的两点，()()1212 0m x x y y =--<，∴该函数图象是y 随x 的增大而减小，∴10a +<，解得1a <-．故答案为：1a <-．【点拨】本题考查了一次函数图象上点的坐标特征，要根据函数的增减性进行推理．19．【分析】由一次函数y =2x +4的图象与x 轴、y 轴的交点分别为A ，B ，可求A （-2，0），B （0，4），在Rt △AOB 中，由勾股定理得AB ==．解：∵一次函数y =2x +4的图象与x 轴、y 轴的交点分别为A 、B ，∴当y =0时，240x +=，解得x =-2，∴A （-2，0），∴当x =0时，y=4，∴B （0，4），∵∠AOB =90°，在Rt △AOB 中，OA =2，OB =4，由勾股定理得AB ===．故答案为：【点拨】本题考查直线与两轴的交点坐标，勾股定理，掌握直线与两轴的交点坐标，勾股定理是解题关键．20．-1【分析】由k =-2＜0，可得出y 随x 的增大而减小，结合-2≤x ≤1，即可求出y 的最小值．解：∵k =-2＜0，∴y 随x 的增大而减小，∴当x =1时，y 取得最小值，此时y =-2×1+1=-1．故答案为：-1．【点拨】本题考查了一次函数的性质，牢记“k ＞0，y 随x 的增大而增大；k ＜0，y 随x 的增大而减小”是解题的关键．21．2x >-【分析】根据一次函数2y kx k =+，可以求得0y =时x 的值，然后根据函数图象和一次函数的性质，可以写出当0y >时，x 的取值范围．解：∵()22y kx k k x =+=+，∴当0y =时，2x =-，由图象可知，y 随x 的增大而增大，∴当0y >时，则x 的取值范围是2x >-，故答案为：2x >-．【点拨】本题考查一次函数图象和性质．根据函数图象判断其增减性是解答本题的关键．22．(20202,2【分析】根据题意可以写出A 和B 的前几个点的坐标，从而可以发现各点的变化规律，从而可以写出点A 2021的坐标．解：∵直线y =，点A 1坐标为（1，0），当1x =时，y ==∴点B 1的坐标为（1，在Rt △OA 1B 1中，OA 1=1，A 1B 1∴12OB =，∴点A 2坐标为（2，0），同理，点B 2的坐标为（2，，点A 3坐标为（4，0），点B 3的坐标为（4，，……∴点B n 的坐标为（2n -1，2n ，当n =2021时，点B 2021的坐标为（22020，2，故答案为：（22020，2．【点拨】本题考查一次函数图象上点的坐标特征、规律型，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．23．（1）一次函数的表达式是y=-2x+1,（2）所围成的三角形面积为14.【分析】把两点坐标分别代入解析式，再解出k,b 即可求出解析式；（2）先根据解析式先求出直线与坐标轴的交点，再利用三角形面积公式求解.解：（1）依题意得323k b k b -+=⎧⎨+=-⎩解得21k b =-⎧⎨=⎩∴所求一次函数的表达式是y=-2x+1,（2）令x ＝0，由y=-2x+1得，y ＝1，令y ＝0，由y=-2x+1，得x ＝12,∴直线AB 与坐标轴的交点坐标分别是（0,1）和（102）∴所围成的三角形面积为：1111224⨯⨯=.24．（1）y =-4x +6000；（2）400张【分析】（1）运用待定系数法解答即可；（2）根据（1）结果算出当x =0时y 的值，用总内存减去此时y 的值即可得到视频文件占用的内存然后求出每张照片的内存，由此求解即可；解：（1）设y 与x 之间的关系式为y ＝kx +b ，根据题意得，10056001505400k b k b +=⎧⎨+=⎩，解得46000k b =-⎧⎨=⎩，故y 与x 之间的关系式为y ＝-4x +6000；（2）当x =0时，y =6000，此时U 盘没有储存照片，只有一个视频文件，8G=8⨯1024MB=8192MB ，8192-6000=2192（MB ）∴U 盘中视频文件的占用内存容量为2192MB ；当x ＝1100时，y ＝-4×1100+6000＝1600，∴此时U 盘有1600MB 内存，当x ＝100时，y ＝5600，∴每张照片的内存为（8192-2192-5600）÷100=4MB ，1600÷4=400（张）∴最多还能存入400张照片．答：最多还能存入400张照片．【点拨】本题主要考查了一次函数的应用，熟练掌握待定系数法求函数关系式是解答本题的关键．25．（1）223y x =-+；（2）56APM S ∆=；（3）1(2,0),13k -≤<．【分析】（1）将点A （0，2）和C （6，﹣2）代入y kx b =+，待定系数法求一次函数解析式即可；（2）根据2y kx k +＝过点M 4(1,3求出解析式，求出求S △APM ；（3）2(2)y kx k k x +=+＝过定点，分别求出P 在AB 、两点的时的k 即可．解：（1）点A （0，2）和C （6，﹣2）代入，y kx b =+得：262b k b =⎧⎨+=-⎩，解得232k b ⎧=-⎪⎨⎪=⎩223y x ∴=-+．（2）2y kx k + ＝过M 4(1,)3442,39k k k ∴+==4899y x ∴=+ A （0，2），B （4，2）,点P 是线段AB 上的动点2y P ∴=直线l 2：y ＝kx +2k （k ≠0）经过点P4852992x x =+=5(,2)2P ∴52PA =14(2)23APM S PA ∆∴=⨯⨯-154(2223=⨯⨯-56=56APM S ∆∴=．（3）2(2)y kx k k x +=+ ＝∴过定点(2,0)-当点P 经过A （0，2）时，代入2y kx k=+22k =，解得1k =当点P 经过B （4，2）时，代入2y kx k=+422k k +=，解得13k =当点P 从点A 到点B 的移动过程中，k 的值在不断变小，点P 不与点A 重合．113k ∴≤<．【点拨】本题考查了，待定系数法求一次函数解析式，一次函数围成的三角形面积，过定点的一次函数，通过数形结合，理解题意，正确的解得一次函数解析式是解题的关键．26．（1）y =20x -300；（2）15【分析】（1）根据图象，用待定系数法即可求出函数的解析式；（2）根据解析式取y =0，求出对应的x 即可．解：（1）设y =kx +b ，代入（20，100），（30，300），得：1002030030k b k b =+⎧⎨=+⎩，解得：20300k b =⎧⎨=-⎩，∴y =20x -300；（2）取y =0，则20x -300=0，解得x =15，∴免费行李的最大质量为15kg ．【点拨】本题主要考查一次函数的图形，关键是能根据图象用待定系数法求出函数的解析式，然后根据y 的值即可求出x 的值．27．(1) 1k =或1k =-；(2)1 32P ⎛⎫ ⎪⎝⎭，解：分析：（1）令0y =，求得x 的值，即可求得A 的坐标为()20，，由OC OA =得()02C ，或()02-，，然后根据待定系数法即可求得k 的值；（2）由()()0402B C ，，，，根据题意求得P 的纵坐标，代入24y x =-+即可求得横坐标．详解：()1由直线24y x =-+与x 轴交于点A ，与y 轴交于点B ，令0y =，则240x -+=，解得2x =，()20A ∴，，OC OA = ，()02C ，∴或()02-，，直线(y kx b k b =+，是常数，0)k ≠经过点A 和点C ，202k b b +=⎧∴⎨=-⎩或202k b b +=⎧⎨=⎩，解得1k =或1k =-；()()()20402B C ，，，，且PC PB =，P ∴的纵坐标为3，点P 在直线24y x =-+上，把3y =代入24y x =-+解得12x =，132P ⎛⎫∴ ⎪⎝⎭，．点睛：考查了待定系数法求一次函数的解析式以及一次函数的图象与性质.注意待定系数法在求函数解析式中的应用.28．（1）(6，0)；（2）4.解：试题分析：（1）先利用直线y=x上的点的坐标特征得到点M的坐标为（2，2），再把M（2，2）代入y=﹣12x+b可计算出b=3，得到一次函数的解析式为y=﹣12x+3，然后根据x轴上点的坐标特征可确定A点坐标为（6，0）；（2）先确定B点坐标为（0，3），则OB=CD=3，再表示出C点坐标为（a，﹣12a+3），D点坐标为（a，a），所以a﹣（﹣12a+3）=3，然后解方程即可．试题解析：解：（1）∵点M在直线y=x的图象上，且点M的横坐标为2，∴点M的坐标为（2，2），把M（2，2）代入y=﹣12x+b得﹣1+b=2，解得b=3，∴一次函数的解析式为y=﹣12x+3，把y=0代入y=﹣12x+3得﹣12x+3=0，解得x=6，∴A点坐标为（6，0）；（2）把x=0代入y=﹣12x+3得y=3，∴B点坐标为（0，3），∵CD=OB，∴CD=3，∵PC⊥x轴，∴C点坐标为（a，﹣12a+3），D点坐标为（a，a）∴a﹣（﹣12a+3）=3，∴a=4．考点：两条直线相交或平行问题．。

基础练习6 一次函数学号 姓名 得分一、选择题：（每小题4分，共32分）1．函数y =xx 3-的自变量的取值范围是（ A ） A ．x ≥3 B ．x ＞3 C ．x ≠0且x ≠3D ．x ≠0 2．函数y =3x +1的图象一定通过（ C ）A ．（3，5）B ．（－2，3）C ．（2，7）D ．（4，10）3．一次函数1-=x y 的图象不经过( B ) A ．第一象限 B ． 第二象限 C ． 第三象限 D ． 第四象限4．若函数y =2x +3与y =3x －2b 的图象交x 轴于同一点，则b 的值为（ D ）A ．－3B ．－23C ．9D ．－49 5．一根蜡烛长20cm ，点燃后每小时燃烧5cm ，燃烧时剩下的高度y (cm)与燃烧时间x (小时)的函数关系用图像表示为( B )6．已知函数y =(m 2+2m )x 12-+m m+(2m －3)是x 的一次函数，则常数m 的值为（ B ） A ．－2 B ．1C ．－2或－1D ．2或－17．已知一次函数m x y +=23和n x y +-=21的图象都经过点A (－2，0)，且与y 轴分别交于B 、C 两点，那么△ABC 的面积是（ C ）A ． 2B ． 3C ． 4D ．68．某学校组织团员举行申奥成功宣传活动，从学校骑车出发，先上坡到达A 地后，宣传8分钟；然后下坡到B 地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度仍保持不变，在A 地仍要宣传8分钟，那么他们从B 地返回学校用的时间是（ A ）A ．45.2分钟B ．48分钟C ．46分钟D ．33分钟二、填空题：（每小题4分，共32分）9．若函数(1)3y m x =++图象经过点（1，2），则m = ．-210．若正比例函数x m y )21(-=的图象经过点),(11y x A 和点),(22y x B ，当12x x <时，12y y >，则m 的取值范围是 。

一次函数试题及答案一、选择题1. 下列哪个选项不是一次函数的表达式？A. y = 3x + 5B. y = x^2 + 1C. y = 2x - 3D. y = -4x答案：B2. 一次函数y = 2x + 1的斜率是：A. 1B. 2C. 3D. -1答案：B3. 如果一次函数y = kx + b的图象经过点(1, 5)和(2, 9)，那么k 的值是：A. 2B. 3C. 4D. 5答案：C二、填空题4. 一次函数y = 4x + 3与x轴的交点坐标是________。

答案：(-3/4, 0)5. 已知一次函数y = -x + 2，当x = 0时，y的值为________。

答案：26. 一次函数y = 3x + 7的图象在y轴上的截距是________。

答案：7三、解答题7. 已知一次函数y = kx + b，其中k ≠ 0，且该函数图象经过点A(-1, 6)和点B(2, -3)。

求k和b的值。

解：将点A(-1, 6)代入y = kx + b得：6 = -k + b ①将点B(2, -3)代入y = kx + b得：-3 = 2k + b ②由①②两式联立解得：k = -3，b = 98. 一次函数y = 5x - 4的图象在x轴上的截距是多少？解：令y = 0，解得：5x - 4 = 0x = 4/5因此，图象在x轴上的截距是4/5。

9. 已知一次函数y = 2x + 1，求当y = 0时，x的值。

解：令y = 0，解得：2x + 1 = 0x = -1/2四、应用题10. 某公司生产一种产品，每件产品的成本为c元，该公司计划以每件产品p元的价格出售。

已知该公司的总成本为C万元，总收入为P万元，且C = 100c，P = 150p。

如果该公司希望获得的利润为20万元，求每件产品的成本c。

解：利润 = 总收入 - 总成本20 = 150p - 100c又因为p = c + 利润/件产品，代入上式得：20 = 150(c + 利润/件产品) - 100c解得c = 40注意：以上试题及答案仅供格式排版参考，具体内容需根据实际教学要求进行调整。

是 ________．
m 的取值范围
3．某一次函数的图像经过点（ -1， 2），且函数 y 的值随 x 的增大而减小，请你写出一个 符合上述条件的函数关系式： _________．
4．已知直线 y=-2x+m 不经过第三象限，则 m 的取值范围是 _________． 5．函数 y=-3x+2 的图像上存在点 P，使得 P?到 x?轴的距离等于 3， ?则点 P?的坐标为
3．直线 y=-2x+4 与两坐标轴围成的三角形的面积是（
）
（ A） 4
（ B） 6
（ C） 8
（ D）16
4 ．若甲、乙两弹簧的长度 y（ cm）与所挂物体质量 x
（ kg）之间的函数解析式分别为 y=k1x+a1 和 y=k2x+a2，
如图，所挂物体质量均为 2kg 时，甲弹簧长为 y1，乙
弹簧长为 y2，则 y1 与 y2 的大小关系为（ ）
0,
∴图像不经过第二象限，故应选
B．
b0
7．B 提示：∵ y=kx+2 经过（ 1 ，1），∴ 1=k+2，∴ y=-x+2，
∵ k=-1<0，∴ y 随 x 的增大而减小，故 B 正确．
∵ y=-x+2 不是正比例函数，∴其图像不经过原点，故
C 错误．
∵ k<0， b=?2>0，∴其图像经过第二象限，故 D 错误．
得 2k p 1 解得 k=-2， p=5， 3k p 1
∴ y 与 x 之间的函数关系是 y=-2x+5； （ 2）∵ 1≤ x≤ 4，把 x1=1， x2=4 分别代入 y=-2x+5，得 y1=3， y 2=-3．

一次函数基础练习题一、选择题1. 下列哪个选项表示一次函数的一般形式？（）A. y = ax² + bx + cB. y = ax + bC. D. y = x² + 12. 一次函数y = 3x 2的图象经过（）象限。

A. 第一、二象限B. 第一、三象限C. 第一、二、三象限D. 第一、二、四象限3. 当k > 0时，一次函数y = kx + b的图象经过（）。

A. 第一、二象限B. 第一、三象限C. 第一、二、三象限D. 第一、二、四象限4. 下列哪个一次函数的图象是一条水平线？（）A. y = 2x + 3B. y = 4C. y = x + 1D. y = x²二、填空题1. 一次函数的图象是一条______。

2. 一次函数y = 2x + 1的斜率为______，截距为______。

3. 若一次函数y = kx + b的图象经过点(1, 3)和(2, 5)，则k=______，b =______。

4. 当x =______时，一次函数y = 3x + 9的值为0。

三、解答题1. 已知一次函数y = kx + b的图象经过点(2, 5)和(4, 9)，求该一次函数的解析式。

2. 一次函数y = 2x + 6的图象与x轴、y轴分别交于点A、B，求线段AB的长度。

3. 画出一次函数y = x 1的图象，并标出其斜率和截距。

4. 已知一次函数y = kx + 3与y = x + 4的图象相交于点P，求点P的坐标。

5. 讨论一次函数y = kx + b的图象与坐标轴的交点情况，当k和b取不同值时，分别画出相应的图象。

四、判断题1. 一次函数的图象一定经过原点。

（）2. 一次函数的斜率决定了图象的倾斜程度，斜率越大，图象越陡峭。

（）3. 一次函数的截距b表示图象与y轴的交点的横坐标。

（）4. 两个一次函数的图象如果平行，则它们的斜率一定相等。

（）5. 一次函数y = kx的图象一定是一条经过原点的直线。

（人教版）八年级数学下册《一次函数》基础测试卷及答案一、选择题(每小题4分,共12分)1·下列函数:(1)y=-8x,(2)y=3·8,(3)y=9x2,(4)y=5x+8,其中是一次函数的有( ) A·0个B·1个C·2个D·3个2·若y+2与2x-3成正比例,则y是x的( )A·正比例函数B·一次函数C·没有函数关系D·以上答案均不正确3·某山山脚的气温是10℃,此山高度每上升1km,气温下降6℃,设比山脚高出xkm处的气温为y℃,y与x之间的函数解析式为( ) A·y=10-6x B·y=10+6xC·y=6-10x D·y=6x-10二、填空题(每小题4分,共12分)4·下列函数:①y=-3x2+4;②y=x-2;③y=x+3;④y=+1;⑤y=-x,其中是一次函数的有(只写序号)·5·已知函数y=(k+2)x+k2-4,当k 时,它是一次函数·当k=_________时,它是正比例函数·6·某企业对自己生产的某种产品进行市场调查,得出这种产品的市场需求量y(千件)和单价x(元)之间的关系式是y=15-3x·(1)单价为2元时,市场需求量是千件·(2)如果单价为5元,那么可能出现的情况是·三、解答题(共26分)7·(8分)已知函数y=(k-2)+b+1是一次函数,求k和b的取值范围·8·(8分)(2012·广州中考)某城市居民用水实行阶梯收费,每户每月用水量如果未超过20t,按每吨1·9元收费·如果超过20t,未超过的部分按每吨1·9元收费,超过的部分按每吨2·8元收费·设某户每月用水量为xt,应收水费为y元·(1)分别写出每月用水量未超过20t和超过20t,y与x之间的函数解析式·(2)若该城市某户5月份水费平均为每吨2·2元,求该户5月份用水多少吨?【拓展延伸】9·(10分)生态公园计划在园内的坡地上造一片有A,B两种树的混合林,需要购买这两种树苗共2000棵,种植A,B两种树苗的相关信息如表:项目品种单价(元/棵)成活率劳务费(元/棵)A 15 95% 3B 20 99% 4设购买A种树苗x棵,造这片林的总费用为y元,解答下列问题: (1)写出y(元)与x(棵)之间的函数解析式·(2)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?答案解析1·【解析】选C·(1)y=-8x符合一次函数的定义,故是一次函数·(2)y=3·8,自变量次数为0,故不是一次函数·(3)y=9x2,自变量次数为2,故不是一次函数·(4)y=5x+8,符合一次函数的定义,故是一次函数·综上可得(1)(4)是一次函数,共2个·2·【解析】选B·由题意可设y+2=k(2x-3)(k≠0),整理得,y=2kx-3k-2,其中2k与-3k-2都是常数且2k≠0,所以y是x的一次函数·3·【解析】选A·根据气温=山脚的气温-下降的气温可得:y=10-6x·4·【解析】①中自变量的次数是2,④中自变量的次数不是1;所以①④不是一次函数,②③⑤均符合一次函数的定义·答案:②③⑤5·【解析】根据一次函数的定义得,k+2≠0,解得k≠-2·函数y=(k+2)x+k2-4是正比例函数,则k+2≠0,k2-4=0,解得k=2·答案:≠-2 26·【解析】(1)当x=2时,y=15-3×2=9·(2)当x=5时,y=15-3×5=0,说明当单价为5元时,这种产品的市场需求量为0,可能会因定价过高而造成产品大量积压·答案:(1)9 (2)产品大量积压7·【解析】根据题意得:k2-3=1,且k-2≠0,∴k=-2或k=2(舍去),∴k=-2·b是任意的常数·8·【解析】(1)当x≤20时,y=1·9x;当x>20时,y=1·9×20+(x-20)×2·8=2·8x-18·(2)用水量如果未超过20t,按每吨1·9元收费·因为5月份水费平均为每吨2·2元,所以用水量超过了20t·所以2·8x-18=2·2x,解得x=30·答:该户5月份用水30t·9·【解析】(1)y=(15+3)x+(20+4)(2000-x)=-6x+48000·(2)由题意可得:0·95x+0·99(2000-x)=1960·x=500,y=-6×500+48000=45000·所以造这片林的总费用需45000元·。

一次函数试题及答案### 一次函数试题一、选择题1. 如果直线y=3x+4与x轴相交于点A(-4/3, 0)，则直线y=3x+b与x 轴相交于点B(x, 0)，则b的值是（）。

- A. 4- B. 12- C. -4- D. 02. 已知一次函数y=kx+b的图象过点(3,5)和(-1,-1)，则k+b的值是（）。

- A. 4- B. 3- C. 2- D. 1二、填空题1. 一次函数y=kx+b的斜率为2，且过点(1,-1)，求b的值。

2. 直线y=-2x+3与y轴的交点坐标是（）。

三、解答题1. 已知一次函数y=kx+b的图象经过点(-1,2)和(2,-1)，求k和b的值。

2. 直线y=-x+3与x轴相交于点A，与y轴相交于点B，求AB的长度。

答案一、选择题1. 答案：B解析：已知直线y=3x+4与x轴相交于点A(-4/3, 0)，因此当y=0时，x=-4/3。

直线y=3x+b与x轴相交时，y=0，所以3x+b=0，解得x=-b/3。

因为交点B的横坐标是x，所以-b/3=x，即b=3x。

将点A的横坐标-4/3代入得b=12。

2. 答案：C解析：将点(3,5)代入y=kx+b得3k+b=5，将点(-1,-1)代入得-k+b=-1。

解方程组得k=2，b=1，所以k+b=3。

二、填空题1. 答案：b=-3解析：已知斜率k=2，将点(1,-1)代入y=kx+b得-1=2*1+b，解得b=-3。

2. 答案：(0,3)解析：直线与y轴相交时，x=0，代入y=-2x+3得y=3。

三、解答题1. 解：将点(-1,2)代入y=kx+b得-k+b=2，将点(2,-1)代入得2k+b=-1。

解方程组得k=-3/2，b=-2。

2. 解：直线y=-x+3与x轴相交时，y=0，代入得x=3，所以点A(3,0)。

与y轴相交时，x=0，代入得y=3，所以点B(0,3)。

根据两点间距离公式，AB=√(3²+3²)=3√2。

一次函数基础测试题含答案一、选择题1．弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂重物的质量x（kg）有下面的关系，那么弹簧总长y（cm）与所挂重物x（kg）之间的关系式为（）x（kg）0123456y（cm）1212.51313.51414.515A．y=0.5x+12 B．y=x+10.5 C．y=0.5x+10 D．y=x+12【答案】A【解析】分析：由上表可知12.5-12=0.5，13-12.5=0.5，13.5-13=0.5，14-13.5=0.5，14.5-14=0.5，15-14.5=0.5，0.5为常量，12也为常量．故弹簧总长y（cm）与所挂重物x（㎏）之间的函数关系式．详解：由表可知：常量为0.5；所以，弹簧总长y（cm）与所挂重物x（㎏）之间的函数关系式为y=0.5x+12．故选A．点睛：本题考查了函数关系，关键在于根据图表信息列出等式，然后变形为函数的形式．2．一次函数y=ax+b与反比例函数a byx-=，其中ab＜0，a、b为常数，它们在同一坐标系中的图象可以是（）A．B．C．D．【答案】C【解析】【分析】根据一次函数的位置确定a、b的大小，看是否符合ab<0，计算a-b确定符号，确定双曲线的位置．【详解】A. 由一次函数图象过一、三象限，得a>0，交y轴负半轴，则b<0，满足ab<0，∴a−b>0，∴反比例函数y=a bx-的图象过一、三象限，所以此选项不正确；B. 由一次函数图象过二、四象限，得a<0，交y轴正半轴，则b>0，满足ab<0，∴a−b<0，∴反比例函数y=a bx-的图象过二、四象限，所以此选项不正确；C. 由一次函数图象过一、三象限，得a>0，交y轴负半轴，则b<0，满足ab<0，∴a−b>0，∴反比例函数y=a bx-的图象过一、三象限，所以此选项正确；D. 由一次函数图象过二、四象限，得a<0，交y轴负半轴，则b<0，满足ab>0，与已知相矛盾所以此选项不正确；故选C.【点睛】此题考查反比例函数的图象，一次函数的图象，解题关键在于确定a、b的大小3．如图，一次函数y＝﹣x+4的图象与两坐标轴分别交于A、B两点，点C是线段AB上一动点（不与点A、B重合），过点C分别作CD、CE垂直于x轴、y轴于点D、E，当点C从点A出发向点B运动时，矩形CDOE的周长（）A ．逐渐变大B ．不变C ．逐渐变小D ．先变小后变大【答案】B【解析】【分析】 根据一次函数图象上点的坐标特征可设出点C 的坐标为(m ，-m+4)(0<m<4)，根据矩形的周长公式即可得出C 矩形CDOE =8，此题得解．【详解】解：设点C 的坐标为(m ，-m+4)(0＜m ＜4)，则CE=m ，CD=-m+4，∴C 矩形CDOE =2(CE+CD)=8．故选B ．【点睛】本题考查了一次函数图象上点的坐标特征以及矩形的性质，根据一次函数图象上点的坐标特征设出点C 的坐标是解题的关键．4．下列函数中，y 随x 的增大而增大的函数是（ ）A ．2y x =-B ．21y x =-+C ．2y x =-D ．2y x =-- 【答案】C【解析】【分析】根据一次函数的性质对各选项进行逐一分析即可．【详解】∵y=-2x 中k=-2＜0，∴y 随x 的增大而减小，故A 选项错误；∵y=-2x+1中k=-2＜0，∴y 随x 的增大而减小，故B 选项错误；∵y=x-2中k=1＞0，∴y 随x 的增大而增大，故C 选项正确；∵y=-x-2中k=-1＜0，∴y 随x 的增大而减小，故D 选项错误．故选C ．【点睛】本题考查的是一次函数的性质，一次函数y=kx+b （k≠0）中，当k ＞0时y 随x 的增大而增大；k<0时y 随x 的增大而减小；熟练掌握一次函数的性质是解答此题的关键．5．若一个正比例函数的图象经过A （3，﹣6），B （m ，﹣4）两点，则m 的值为（ ）A．2 B．8 C．﹣2 D．﹣8【答案】A【解析】试题分析：设正比例函数解析式为：y=kx，将点A（3，﹣6）代入可得：3k=﹣6，解得：k=﹣2，∴函数解析式为：y=﹣2x，将B（m，﹣4）代入可得：﹣2m=﹣4，解得m=2，故选A．考点：一次函数图象上点的坐标特征．=-+的图象大致是( )6．已知点(k，b)为第二象限内的点，则一次函数y kx bA．B．C．D．【答案】D【解析】【分析】根据已知条件“点（k，b）为第二象限内的点”推知k、b的符号，由它们的符号可以得到一次函数y=-kx+b的图象所经过的象限．【详解】解：∵点（k，b）为第二象限内的点，∴k＜0，b＞0，∴-k＞0．∴一次函数y=-kx+b的图象经过第一、二、三象限，观察选项，D选项符合题意．故选：D．【点睛】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限；k＜0时，直线必经过二、四象限；b＞0时，直线与y轴正半轴相交；b=0时，直线过原点；b ＜0时，直线与y轴负半轴相交．7．如图，直线y=kx+b（k≠0）经过点A（﹣2，4），则不等式kx+b＞4的解集为（）A．x＞﹣2 B．x＜﹣2 C．x＞4 D．x＜4【答案】A【解析】【分析】求不等式kx+b ＞4的解集就是求函数值大于4时，自变量的取值范围，观察图象即可得.【详解】由图象可以看出，直线y=4上方函数图象所对应自变量的取值为x>-2， ∴不等式kx+b ＞4的解集是x>-2，故选A ．【点睛】本题考查了一次函数与一元一次不等式；观察函数图象，比较函数图象的高低（即比较函数值的大小），确定对应的自变量的取值范围．也考查了数形结合的思想．8．一次函数y kx b +＝的图象与正比例函数6y x ＝﹣的图象平行且经过点A （1，-3），则这个一次函数的图象一定经过( )A ．第一、二、三象限B ．第一、三、四象限C ．第一、二、四象限D ．第二、三、四象限【答案】C【解析】【分析】 由一次函数y kx b +＝的图象与正比例函数6y x ＝﹣的图象平行可得k=-6，把点A 坐标代入y=-6x+b 可求出b 值，即可得出一次函数解析式，根据一次函数的性质即可得答案．【详解】∵一次函数y kx b +＝的图象与正比例函数6y x ＝﹣的图象平行， ∴k=-6，∵一次函数6y x b =-+经过点A （1，-3），∴-3=-6+b ，解得：b=3，∴一次函数的解析式为y=-6x+3，∵-6＜0，3＞0，∴一次函数图象经过二、四象限，与y 轴交于正半轴，∴这个一次函数的图象一定经过一、二、四象限，故选：C ．【点睛】本题考查了两条直线平行问题及一次函数的性质：若直线y=k 1x+b 1与直线y=k 2x+b 2平行，则k 1=k 2；当k ＞0时，图象经过一、三象限，y 随x 的增大而增大；当k ＜0时，图象经过二、四象限，y 随x 的增大而减小；当b ＞0时，图象与y 轴交于正半轴；当b ＜0时，图象与y 轴交于负半轴．9．如图，直线l 是一次函数y=kx+b 的图象，若点A （3，m ）在直线l 上，则m 的值是（ ）A ．﹣5B ．32C ．52D ．7【答案】C【解析】【分析】 把（-2，0）和（0，1）代入y=kx+b ，求出解析式，再将A （3，m ）代入，可求得m.【详解】把（-2，0）和（0，1）代入y=kx+b ，得201k b b -+=⎧⎨=⎩， 解得121k b ⎧=⎪⎨⎪=⎩ 所以，一次函数解析式y=12x+1， 再将A （3，m ）代入，得 m=12×3+1=52. 故选C.【点睛】 本题考核知识点：考查了待定系数法求一次函数的解析式,根据解析式再求函数值.10．若正比例函数y ＝kx 的图象经过第二、四象限，且过点A (2m ，1)和B (2，m )，则k 的值为( )A ．﹣12B ．﹣2C ．﹣1D ．1【答案】A【解析】【分析】根据函数图象经过第二、四象限，可得k ＜0，再根据待定系数法求出k 的值即可．【详解】解：∵正比例函数y ＝kx 的图象经过第二、四象限，∴k ＜0．∵正比例函数y ＝kx 的图象过点A (2m ，1)和B (2，m )，∴2km 12k m =⎧⎨=⎩， 解得：m 11k 2=-⎧⎪⎨=-⎪⎩或m 11k 2=⎧⎪⎨=⎪⎩(舍去)． 故选：A ．【点睛】本题考查了正比例函数的系数问题，掌握正比例函数的性质、待定系数法是解题的关键．11．在平面直角坐标系中，函数2(0)y kx k =≠的图象如图所示，则函数232y kx k =-+的图象大致是（）A ．B ．C ．D ．【答案】C【解析】【分析】根据函数图象易知k 0<，可得32k 0-+<，所以函数图象沿y 轴向下平移可得．【详解】解：根据函数图象易知k 0<，∴32k 0-+<，故选：C ．【点睛】此题主要考查一次函数的性质与图象，正确理解一次函数的性质与图象是解题关键．12．已知直线y1=kx+1（k＜0）与直线y2=mx（m＞0）的交点坐标为（12，12m），则不等式组mx﹣2＜kx+1＜mx的解集为（）A．x>12B．12<x<32C．x<32D．0<x<32【答案】B 【解析】【分析】由mx﹣2＜（m﹣2）x+1，即可得到x＜32；由（m﹣2）x+1＜mx，即可得到x＞12，进而得出不等式组mx﹣2＜kx+1＜mx的解集为12＜x＜32．【详解】把（12，12m）代入y1=kx+1，可得1 2m=12k+1，解得k=m﹣2，∴y1=（m﹣2）x+1，令y3=mx﹣2，则当y3＜y1时，mx﹣2＜（m﹣2）x+1，解得x＜32；当kx+1＜mx时，（m﹣2）x+1＜mx，解得x＞12，∴不等式组mx﹣2＜kx+1＜mx的解集为12＜x＜32，故选B．【点睛】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．13．超市有A，B两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，且无剩油）；当日促销活动：购买A型瓶3个或以上，一次性返还现金5元，设购买A型瓶x（个），所需总费用为y（元），则下列说法不一定成立的是（）A ．购买B 型瓶的个数是253x ⎛⎫- ⎪⎝⎭为正整数时的值 B ．购买A 型瓶最多为6个C ．y 与x 之间的函数关系式为30y x =+D ．小张买瓶子的最少费用是28元 【答案】C【解析】【分析】设购买A 型瓶x 个,B(253x -)个,由题意列出算式解出个选项即可判断. 【详解】设购买A 型瓶x 个， ∵买瓶子用来分装15升油，瓶子都装满，且无剩油，∴购买B 型瓶的个数是1522533x x -=-, ∵瓶子的个数为自然数,∴x=0时, 253x -=5; x=3时, 253x -=3; x=6时, 253x -=1; ∴购买B 型瓶的个数是(253x -)为正整数时的值，故A 成立; 由上可知，购买A 型瓶的个数为0个或3个或6个，所以购买A 型瓶的个数最多为6，故B 成立;设购买A 型瓶x 个，所需总费用为y 元，则购买B 型瓶的个数是(253x -)个， ④当0≤x<3时，y=5x+6×(253x -)=x+30， ∴k=1>0，∴y 随x 的增大而增大，∴当x=0时，y 有最小值，最小值为30元;②当x≥3时，y=5x+6×(253x -)-5=x+25， ∵.k=1>0随x 的增大而增大，∴当x=3时，y 有最小值，最小值为28元;综合①②可得，购买盒子所需要最少费用为28元.故C 不成立，D 成立故选:C.【点睛】本题考查一次函数的应用,关键在于读懂题意找出关系式.14．将直线23y x =-向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为（ ）A ．24y x =-B ．24y x =+C ．22y x =+D ．22y x =- 【答案】A【解析】【分析】直接根据“上加下减”、“左加右减”的原则进行解答即可．【详解】由“左加右减”的原则可知，将直线y=2x-3向右平移2个单位后所得函数解析式为y=2(x-2)-3=2x-7，由“上加下减”原则可知，将直线y=2x-7向上平移3个单位后所得函数解析式为y=2x-7+3=2x-4，故选A.【点睛】本题考查了一次函数的平移，熟知函数图象平移的法则是解答此题的关键．15．生物活动小组的同学们观察某植物生长，得到该植物高度y (单位：cm )与观察时间x (单位：天)的关系，并画出如图所示的图象(//CD x 轴)，该植物最高的高度是( )A ．50cmB ．20cmC ．16cmD ．12cm【答案】C【解析】【分析】 设直线AC 的解析式为()0y kx b k =+≠，然后利用待定系数法求出直线AC 的解析式，再把50x =代入进行计算即可得解．【详解】解：设直线AC 的解析式为()0y kx b k =+≠∵()0,6A ，()30,12B∴61230b k b =⎧⎨=+⎩∴156k b ⎧=⎪⎨⎪=⎩ ∴165y x =+ ∴当50x =时，16y =∴该植物最高的高度是16cm ．故选：C【点睛】本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，已知自变量求函数值，仔细观察图象，准确获取信息是解题的关键．16．如图，已知直线1y x b =+与21y kx =-相交于点P ，点P 的横坐标为1-，则关于x 的不等式1x b kx +≤-的解集在数轴上表示正确的是（ ）．A ．B ．C ．D ．【答案】D【解析】 试题解析：当x ＞-1时，x+b ＞kx-1，即不等式x+b ＞kx-1的解集为x ＞-1．故选A ．考点：一次函数与一元一次不等式.17．在平面直角坐标系中，已知直线与轴、轴分别交于、两点，点是轴上一动点，要使点关于直线的对称点刚好落在轴上，则此时点的坐标是（ ） A ． B ． C ． D ．【答案】B【解析】【分析】过C 作CD ⊥AB 于D ，先求出A ，B 的坐标，分别为（4，0），（0，3），得到AB 的长，再根据折叠的性质得到AC 平分∠OAB ，得到CD=CO=n ，DA=OA=4，则DB=5-4=1，BC=3-n ，在Rt △BCD 中，利用勾股定理得到n 的方程，解方程求出n 即可．【详解】过C 作CD ⊥AB 于D ，如图，对于直线，当x=0，得y=3；当y=0，x=4， ∴A （4，0），B （0，3），即OA=4，OB=3，∴AB=5，又∵坐标平面沿直线AC 折叠，使点B 刚好落在x 轴上，∴AC 平分∠OAB ，∴CD=CO=n ，则BC=3-n ，∴DA=OA=4，∴DB=5-4=1，在Rt △BCD 中，DC 2+BD 2=BC 2，∴n 2+12=（3-n ）2，解得n=，∴点C 的坐标为（0，）．故选B.【点睛】本题考查了一次函数图象与几何变换：直线y=kx+b ，（k≠0，且k ，b 为常数），关于x 轴对称，横坐标不变，纵坐标是原来的相反数；关于y 轴对称，纵坐标不变，横坐标是原来的相反数；关于原点轴对称，横、纵坐标都变为原来的相反数．也考查了折叠的性质和勾股定理．18．对于一次函数24y x =-+，下列结论正确的是（ ）A ．函数值随自变量的增大而增大B ．函数的图象不经过第一象限C ．函数的图象向下平移4个单位长度得2y x =-的图象D ．函数的图象与x 轴的交点坐标是()0,4【答案】C【解析】【分析】根据一次函数的系数结合一次函数的性质，即可得知A 、B 选项不正确，代入y=0求出与之对应的x 值，即可得出D 不正确，根据平移的规律求得平移后的解析式，即可判断C 正确，此题得解．【详解】解：A 、∵k=-2＜0，∴一次函数中y 随x 的增大而减小，故 A 不正确；B 、∵k=-2＜0，b=4＞0，∴一次函数的图象经过第一、二、四象限，故B 不正确；C 、根据平移的规律，函数的图象向下平移4个单位长度得到的函数解析式为y=-2x+4-4，即y=-2x ，故C 正确；D 、令y=-2x+4中y=0，则x=2，∴一次函数的图象与x 轴的交点坐标是（2，0）故D 不正确．故选：C ．【点睛】此题考查一次函数的图象以及一次函数的性质，解题的关键是逐条分析四个选项．本题属于基础题，难度不大，解决该题时，熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键．19．已知一次函数y ＝kx+k ，其在直角坐标系中的图象大体是（ ）A ．B ．C ．D ．【答案】A【解析】【分析】函数的解析式可化为y=k（x+1），易得其图象与x轴的交点为（﹣1，0），观察图形即可得出答案．【详解】函数的解析式可化为y=k（x+1），即函数图象与x轴的交点为（﹣1，0），观察四个选项可得：A符合．故选A．【点睛】本题考查了一次函数的图象，要求学生掌握通过解析判断其图象与坐标轴的交点位置、坐标．20．函数y=2x﹣5的图象经过（）A．第一、三、四象限B．第一、二、四象限C．第二、三、四象限D．第一、二、三象限【答案】A【解析】【分析】先根据一次函数的性质判断出此函数图象所经过的象限，再进行解答即可．【详解】∵一次函数y=2x-5中，k=2＞0，∴此函数图象经过一、三象限，∵b= -5＜0，∴此函数图象与y轴负半轴相交，∴此一次函数的图象经过一、三、四象限，不经过第二象限．故选A．【点睛】本题考查的是一次函数的性质，即一次函数y=kx+b（k≠0）中，当k＞0时，函数图象经过一、三象限，当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．。

一次函数练习题及答案一、选择题1. 一次函数y = 2x - 3的斜率是：A. 2B. -3C. -2D. 3答案：A2. 如果一次函数y = kx + b的图象经过点(1, 0)和(0, -1)，那么k 的值是：A. 1B. -1C. 0D. 2答案：A3. 函数y = 3x + 5与x轴的交点坐标是：A. (-5/3, 0)B. (0, 5)C. (1, 0)D. (-1, 0)答案：A二、填空题4. 已知一次函数y = 4x + 1，当x = 2时，y的值为________。

答案：95. 一次函数y = -2x + 4的图象与y轴的交点坐标是________。

答案：(0, 4)三、解答题6. 已知直线y = 3x + 2与直线y = -x + 4相交于点P，求点P的坐标。

解：将两个方程联立求解：\[ \begin{cases} y = 3x + 2 \\ y = -x + 4 \end{cases} \]解得：\[ x = \frac{2}{4}, y = 3 \times \frac{2}{4} + 2 \] 所以点P的坐标为(\(\frac{1}{2}\), 3)。

7. 一次函数y = kx + b的图象经过点A(-1, -2)和点B(2, 6)，求k 和b的值。

解：将点A和点B的坐标代入一次函数方程得：\[ \begin{cases} -k + b = -2 \\ 2k + b = 6 \end{cases} \] 解得：\[ k = 2, b = 0 \]8. 已知直线y = 5x - 7在x轴上的截距为a，在y轴上的截距为b，求a和b的值。

解：当y = 0时，x = \frac{7}{5}，所以a = \frac{7}{5}；当x = 0时，y = -7，所以b = -7。

四、应用题9. 某工厂生产一种产品，每件产品的成本为c元，售价为p元。

已知当生产x件时，利润为y元，且利润函数为y = 20x - 30。

一次函数练习题与答案一、选择题1. 一次函数y=kx+b的斜率k表示的是：A. 函数的截距B. 函数的斜率C. 函数的对称轴D. 函数的顶点2. 已知一次函数y=3x-5，当x=2时，y的值是：A. 1B. -1C. 7D. -73. 一次函数y=kx+b的图象过点(-1,6)，且与y轴交于点(0,-2)，则k 的值为：A. 4B. -4C. 8D. -84. 直线y=-2x+b与两坐标轴围成的三角形面积为1，且直线与y轴的交点在x轴上方，则b的值为：A. 1B. 2C. 3D. 45. 一次函数y=kx+b的图象不经过第三象限，那么：A. k>0，b>0B. k<0，b>0C. k>0，b<0D. k<0，b<0二、填空题6. 一次函数y=2x-3与x轴的交点坐标是_________。

7. 一次函数y=-4x+5的图象与x轴相交于点_________。

8. 若一次函数y=kx+b的图象过点(1,0)和(0,-1)，则k=_______，b=_______。

9. 一次函数y=-x+3与直线y=2x-1的交点坐标是_________。

10. 一次函数y=-3x+4的图象与y轴的交点坐标是_________。

三、解答题11. 已知一次函数y=kx+b的图象经过点(-1,10)和(2,5)，求k和b的值。

12. 直线y=kx+b经过原点，且与x轴相交于点(3,0)，求k和b的值。

13. 一次函数y=kx+b的图象与x轴相交于点(a,0)，与y轴相交于点(0,b)，求k和b的值。

14. 已知一次函数y=kx+b的图象经过点(-2,15)和(1,-6)，求k和b的值。

15. 一次函数y=kx+b的图象与两坐标轴围成的三角形面积为4，且直线与x轴的交点在y轴右侧，求k和b的值。

答案：1. B2. A3. B4. B5. D6. (3/2, 0)7. (5/4, 0)8. k=-1，b=19. (1, 2)10. (0, 4)11. k=-5，b=1512. k=-1/3，b=013. k=-a/b，b为y轴交点的y坐标14. k=-11，b=1715. k=4/3，b=-4【注】本练习题旨在帮助学生掌握一次函数的基本性质和求解方法，通过不同类型的题目，加强学生对一次函数图象和性质的理解与应用。

6.4 确定一次函数表达式◆基础训练一、选择题1．如果直线y=kx+b经过A（0，1），B（1，0），则k，b的值为（）．A．k=-1，b=-1 B．k=1，b=1 C．k=1，b=-1 D．k=-1，b=12．图象经过（0，），（-2）的一次函数表达式为（）．A．．C．．3．已知直线y=3x-2与两条坐标轴围成的三角形面积是（）．A．-23B．23C．32D．-32二、填空题4．写出满足下表关系的一个一次函数关系式是______．5．已知y+2与x成正比例，且当x=-1时，y=2，则y与x之间的函数关系式为______．三、解答题6．一次函数的图象过M（3，2），N（-1，-6）两点．（1）求函数的解析式；（2）试通过计算判断点P（2a，4a-4）是否在此函数的图象上．7．已知一次函数y=kx+b的图象与x轴交于点A（-6，0），与y轴交于点B，若△AOB•的面积为12，且y随x的增大而减小，求一次函数的解析式．◆能力提高一、填空题8．直线y=kx+b与直线y=-13x平行，且与y轴的交点的纵坐标是3，那么k=•_____，•b=______．二、解答题9．已知一次函数的自变量的取值范围是2≤x≤6，函数值的范围是5≤y≤9，求这个一次函数的解析式．10．已知两条直线y1=k1x+b1和y2=k2x+b2相交于点（-3，2），并且分别过点（-32，3）和（1，•-2），那么这两条直线与y轴围成的三角形的面积等于多少？◆拓展训练11．已知一次函数的图象交正比例函数图象于点M，交x轴于点N（-6，0），•又知点M位于第二象限，其横坐标为-4，若△MON面积为15，求正比例函数和一次函数的解析式．答案:1．D 2．D 3．B 4．y=-12x+7 5．y=-4x-26．（1）y=2x-4 （2）P点在函数图象上7．∵一次函数图象与y轴交于B，∴B（0，b）． A在一次函数图象上，则-6k+b=0．①△AOB的面积为12，则12OA·OB=12．即12×6×│b│=12，b=±4．代入①式，可得k=±23．而y随x增大而减小，∴k<0，则k=-23．b=-4．∴一次函数的解析式为y=-23x-4．8．-133 9．y=x+3或y=-x+1110．先求出k1=23，b1=4，k2=-1，b2=-1，则面积为12×3×（1+4）=7.511．根据题意画示意图，过点M作MC⊥ON于C．则S△MON=12 ON·MC．∵点N的坐标为（-6，0）．∴│ON│=6，∴12·│ON│·MC=15，∴MC=5．∵点M在第二象限，∴点M的纵坐标y=5，∴点M的坐标为（-4，5）．∵一次函数解析式为y=k1x+b．正比例函数解析式为y=k 2x ，直线y=k 1x+b 经过（-6，0）．∴111506,,25415.k b k k b b ⎧=-+=⎧⎪∴⎨⎨=-+⎩⎪=⎩解得∴一次函数解析式为y=52x+15．∵正比例函数y=kx 图象经过点（-4，5）． ∴k 2=-54，∴正比例函数解析式为y=-54x ．。

一次函数基础练习题（含答案解析）一、选择题（本大题共25小题，共75.0分）1.甲、乙两人进行慢跑练习，慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示，下列说法错误的是()A. 前2分钟，乙的平均速度比甲快B. 5分钟时两人都跑了500米C. 甲跑完800米的平均速度为100米/分D. 甲乙两人8分钟各跑了800米2.小明的父亲饭后出去散步，从家中走20min到一个离家900m的报亭看10min报纸后，用15min返回家里，图中表示小明父亲离家的时间与距离之间的关系是()A. B.C. D.3.下列关系式中，y是x的一次函数的是()+2 D. y=√2A. y=x2B. y=1−3xC. y=12x4.直线y=kx+3经过点A(2,1)，则不等式kx+3≥0的解集是()A. x≤3B. x≥3C. x≥−3D. x≤05.若y=kx+2的函数值y随着x的增大而增大，则k的值可能是()A. 0B. 1C. −30D. −26.对于一次函数y=−2x+4，下列结论错误的是()A. 函数的图象不经过第三象限B. 函数的图象与x轴的交点坐标是(0,4)C. 函数的图象向下平移4个单位长度得y=−2x的图象D. 函数值随自变量的增大而减小7.小明的父亲从家走了20分钟到一个离家900米的书店，在书店看了10分钟书后，用15分钟返回家，下列图中表示小明的父亲离家的距离与时间的函数图象是()A. B.C. D.8.如图，在点M，N，P，Q中，一次函数y=kx+2(k<0)的图象不可能经过的点是()A. MB. NC. PD. Q9.下列各曲线中，不能表示y是x的函数的是()A. B.C. D.10.已知y=kx+b，与x轴，y轴分别交于(2,0)和(0,3)，则当kx+b>3时，x的取值为()A. x<2B. x≤2C. x≤0D. x<011.已知函数y=3x−1，当x=3时，y的值是()A. 6B. 7C. 8D. 9x+b上的两点，则m与n的大小关系是() 12.已知点A(−3,m)与点B(2,n)是直线y=−23A. m>nB. m=nC. m<nD. 无法确定13.点A(1,m)在函数y=2x的图象上，则点A的坐标是()A. (1,0)B. (1,2)C. (1,1)D. (2,1)14.已知点A(−1,m)，B(1,m)，C(2,m+1)在同一个函数图象上，这个函数图象可以是()A. B. C. D.15.)：温度/℃−20−100102030声速/m/s318324330336342348下列说法错误的是()A. 在这个变化中，自变量是温度，因变量是声速B. 温度越高，声速越快C. 当空气温度为20℃时，声音5s可以传播1740mD. 当温度每升高10℃，声速增加6m/s16.已知函数y=2x−1x+2，当x=3时，y的值为()A. 1B. −1C. −2D. −317.如果P(2,m)，A(1,1)，B(4,0)三点在同一直线上，则m的值为()A. 2B. −23C. 23D. 118.函数y=√xx−2的自变量x的取值范围是()A. x≥0且x≠2B. x≥0C. x≠2D. x>219.函数y=√x−2x+4中，自变量x的取值范围是()A. x>4B. x≥2C. x≥2且x≠−4D. x≠−420.有下列函数：①y=2x；②y=−x−100；③y=2−3x；④y=x2−1.其中是一次函数的有()A. 1个B. 2个C. 3个D. 4个21.若点A(−1,2)，B(2,−3)在直线y=kx+b上，则函数y=kx的图象在()A. 第一、三象限B. 第一、二象限C. 第二、四象限D. 第二、三象限22.在某个变化过程中，数值保持不变的量，叫做()A. 函数B. 变量C. 常量D. 自变量23.正比例函数y=(k−2)x中，y随x的增大而减小，则k的取值范围是()A. k≥2B. k≤2C. k>2D. k<224.下列函数中，当x>0时，y的值随x的值增大而增大的是()A. y=−x2B. y=x−1C. y=−x+1D. y=1x25.下列各点，在函数y=−12x的图象上的是()A. (1,2)B. (2,1)C. (1,−2)D. (−2,1)二、填空题（本大题共15小题，共45.0分）26.一次函数y=(4−m)x+m−2的图象经过第一，三，四象限，则m应为______ ．27.在函数y=√x−2x−4中，自变量x的取值范围是______ ．28.写出图象经过点(1,−1)的一个函数关系式______．29.在函数y=√x−1中，自变量x的取值范围是______．30.在一次函数y=2x+3中，y随x的增大而______ .(填“增大”或“减小”)31.某一次函数的图象与直线y1=2x−1平行，但与直线y2=−x+2有交点A，已知点A的横坐标为3，则这个一次函数的解析式为______．32.若函数y=kx+3的图象经过点(3,6)，则k=______．33.已知一次函数f(x)=x−2，若f(x)=1，则x=______．34.若函数y=(a+3)x+a2−9是正比例函数，则a=______ ．35.若一次函数y=−2x+b(b为常数)的图象经过第二、三、四象限，则b的值可以是______ (写出一个即可)．36.一次函数y=kx+b的图象如图所示，则当kx+b>0时，x的取值范围为______．37.如图，函数y=2x和y=ax+4的图象交于点A(m,3)，则方程2x=ax+4的解为x=______．38.已知一次函数y=kx+2k+3的图象不经过第三象限，则k的取值范围为______ ．39.一次函数y=2(x−1)+5的图象在y轴上的截距为______．40.写出一个一次函数的解析式：______，使它经过点A(2,4)且y随x的增大而减小．答案和解析【答案】1. D2. D3. B4. A5. B6. B7. B8. D9. D10. D11. C12. A13. B14. C15. C16. A17. C18. A19. B20. C21. C22. C23. D24. B25. D26. m<227. x≥2且x≠428. y=x2−2x29. x≥130. 增大31. y=2x−732. 133. 334. 335. −136. x>137. 32≤k<038. −3239. 340. y=−x+6【解析】1. 解：前2分钟，乙跑了300米，甲跑的路程小于300米，从而可知前2分钟，乙的平均速度比甲快，故选项A正确；由图可知，5分钟时两人都跑了500米，故选项B正确；由图可知，甲8分钟跑了800米，可得甲跑完800米的平均速度为100米/分，故选项C正确；由图可得，甲8分钟跑了800米，乙8分钟跑了700米，故选项D错误；故选D．根据函数图象可以判断各选项是否正确，从而可以解答本题．本题考查函数的图象，解题的关键是利用数形结合的思想判断选项中的说法是否正确．2. 解：20分钟到报亭离家的距离随时间的增加而增加；看报10分钟，离家的距离不变；15分钟回家离家的距离岁时间的增加而减少，故D选项符合题意．故选(D)根据函数图象的横坐标，可得时间，根据函数图象的纵坐标，可得离家的距离．本题考查了函数图象，根据横轴和纵轴表示的量，得出时间与离家距离的关系是解题关键．3. 解：A、是二次函数，故A错误；B、是一次函数，故B正确；C、是反比例函数的平移，故C错误；D、是常函数，故D错误；故选：B．根据一次函数的定义：y=kx+b(k、b是常数，k≠0)，可得答案．本题考查了一次函数的定义，利用一次函数的定义是解题关键，注意k≠0．4. 解：∵y=kx+3经过点A(2,1)，∴1=2k+3，解得：k=−1，∴一次函数解析式为：y=−x+3，−x+3≥0，解得：x≤3．故选：A．首先把点A(2,1)代入y=kx+3中，可得k的值，再解不等式kx+3≥0即可．此题主要考查了一次函数与一元一次不等式，关键是掌握待定系数法计算出k的值．5. 解：∵y=kx+2的函数值y随着x的增大而增大，∴k>0．故选B先根据一次函数的增减性判断出k的符号，进而可得出结论．本题考查的是一次函数的性质，熟知一次函数的增减性是解答此题的关键．6. 解：A、k=−2，b=4，函数的图象经过第一、二、四象限，不经过第三象限，不符合题意；B、函数的图象与y轴的交点坐标是(0,4)，符合题意；C、函数的图象向下平移4个单位长度得y=−2x的图象，不符合题意；D、k=−2，函数值随自变量的增大而减小，不符合题意；故选B根据一次函数的性质对A、D进行判断；根据一次函数图象上点的坐标特征对B进行判断；根据一次函数的几何变换对C进行判断．本题考查了一次函数的性质：当k>0，y随x的增大而增大，函数从左到右上升；当k<0，y随x的增大而减小，函数从左到右下降.也考查了一次函数图象的几何变换．7. 解：根据题意，从20分钟到30分钟在书店里看书，离家距离没有变化，是一条平行于x轴的线段．故选B．因为在书店里花了10分钟看书，应是一段平行与x轴的线段，B是10分钟，而A是20分钟，依此即可作出判断．考查了函数的图象，本题是常见的函数题，属于分段函数，前面是正比例函数，中间是平行于x轴的一条线段，后面是一次函数．8. 解：∵在y=kx+2(k<0)中，令x=0可得y=2，∴一次函数图象一定经过第一、二象限，∵k<0，∴y随x的增大而减小，∴一次函数不经过第三象限，∴其图象不可能经过Q点，故选：D．由条件可判断出直线所经过的象限，再进行判断即可．本题主要考查一次函数的图象，利用k、b的正负判断一次函数的图象位置是解题的关键，即在y=kx+b中，①k>0，b>0，直线经过第一、二、三象限，②k>0，b<0，直线经过第一、三、四象限，③k<0，b>0，直线经过第一、二、四象限，④k<0，b<0，直线经过第二、三、四象限．9. 解：A，B，C的图象都满足对于x的每一个取值，y都有唯一确定的值与之对应关系，故A、B、C的图象是函数，D的图象不满足满足对于x的每一个取值，y都有唯一确定的值与之对应关系，故D错误；故选：D．根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可确定函数的个数．主要考查了函数的定义.函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．10. 解：当x<0时，函数图象位于x轴左方，可见kx+b>3时，x<0．故选D．充分利用图形，直接从图上得出x的取值范围．此题考查了一次函数与不等式，利用数形结合是解题的关键．11. 解：x=3时，y=3×3−1=8．故选C．把x =3代入函数关系式进行计算即可得解．本题考查了函数值求解，把自变量的值代入函数关系式计算即可，比较简单．12. 解：∵直线y =−23x +b 中，k =−23<0，∴此函数是减函数． ∵−3<2， ∴m >n ． 故选A ．先根据直线的解析式判断出函数的增减性，再根据一次函数的性质即可得出结论．本题考查的是一次函数图象上点的坐标特点，熟知一次函数的增减性是解答此题的关键． 13. 解：∵点A(1,m)在函数y =2x 的图象上， ∴m =2， ∴A(1,2)． 故选B ．直接把点A(1,m)代入函数y =2x ，求出m 的值即可．本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上点的坐标一定适合此函数的解析式是解答此题的关键．14. 解：∵点A(−1,m)，B(1,m)，∴A 与B 关于y 轴对称，故A ，B 错误； ∵B(1,m)，C(2,m +1)，∴当x >0时，y 随x 的增大而增大，故C 正确，D 错误． 故选C ．由点A(−1,m)，B(1,m)，C(2,m +1)在同一个函数图象上，可得A 与B 关于y 轴对称，当x >0时，y 随x 的增大而增大，继而求得答案．此题考查了函数的图象.注意掌握排除法在选择题中的应用是解此题的关键． 15. 解：∵在这个变化中，自变量是温度，因变量是声速， ∴选项A 正确；∵根据数据表，可得温度越高，声速越快， ∴选项B 正确；∵342×5=1710(m)，∴当空气温度为20℃时，声音5s 可以传播1710m ， ∴选项C 错误；∵324−318=6(m/s)，330−324=6(m/s)，336−330=6(m/s)，342−336=6(m/s)，348−342=6(m/s)， ∴当温度每升高10℃，声速增加6m/s ， ∴选项D 正确． 故选：C ．根据自变量、因变量的含义，以及声音在空气中传播的速度与空气温度关系逐一判断即可． 此题主要考查了自变量、因变量的含义和判断，要熟练掌握． 16. 解：当x =3时， y =2x−1x+2=2×3−13+2=1，故选A根据函数值的求解方法，把x =3代入y =2x−1x+2，求出函数y =2x−1x+2的值为多少即可．此题主要考查了函数值的求解，采用代入法即可，要熟练掌握，解答此题的关键是要明确：①当已知函数解析式时，求函数值就是求代数式的值；当已知函数解析式，给出函数值时，求相应的自变量的值就是解方程；②当自变量确定时，函数值是唯一确定的.但当函数值唯一确定时，对应的自变量可以是多个． 17. 解：设直线的解析式为y =kx +b(k ≠0)， ∵A(1,1)，B(4,0)，∴{1=k +b 0=4k +b ，解得{k =−13b =43， ∴直线AB 的解析式为y =−13x +43， ∵P(2,m)在直线上， ∴m =(−13)×2+43=23．故选C ．先设直线的解析式为y =kx +b(k ≠0)，再把A(1,1)，B(4,0)代入求出k 的值，进而得出直线AB 的解析式，把点P(2,m)代入求出m 的值即可．本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．18. 解：由题意得，x ≥0且x −2≠0， 解得x ≥0且x ≠2． 故选A ．根据被开方数大于等于0，分母不等于0列式计算即可得解． 本题考查了函数自变量的范围，一般从三个方面考虑： (1)当函数表达式是整式时，自变量可取全体实数； (2)当函数表达式是分式时，考虑分式的分母不能为0； (3)当函数表达式是二次根式时，被开方数非负．19. 解：由题意得{x +4≠0x−2≥0，解得x ≥2，x ≠−4，∴自变量x 的取值范围是x ≥2， 故选B ．根据分式和二次根式有意义的条件进行选择即可．本题考查了函数自变量的取值范围问题，掌握分式和二次根式有意义的条件是解题的关键． 20. 解：①y =2x 是特殊的一次函数； ②y =−x −100是一次函数； ③y =2−3x 是一次函数； ④y =x 2−1是二次函数， 故选：C ．根据一次函数的定义：y =kx +b(k 、b 是常数，k ≠0)，可得答案．本题考查了一次函数的定义，利用一次函数的定义是解题关键，注意正比例函数是特殊的一次函数，一次函数不一定是正比例函数．21. 解：根据题意，将点A(−1,2)，B(2,−3)代入直线y =kx +b ， 得：{2k +b =−3−k+b=2， 解得：{k =−53b =13，∴由反比例函数的性质可知，k =−53<0时，函数y =kx 的图象在第二、四象限， 故选：C ．待定系数法求得k、b的值，根据反比例函数的图象与性质即可判断．本题主要考查待定系数法求一次函数解析式及反比例函数的图象与性质，熟练掌握待定系数法与反比例函数的图象与性质是解题的关键．22. 解：在某个变化过程中，数值保持不变的量，叫做常量，故选：C．根据常量、变量的定义，可得答案．本题考查了常量与变量，变量是指在程序的运行过程中随时可以发生变化的量，在某个变化过程中，数值保持不变的量，叫做常量．23. 解：∵正比例函数y=(k−2)x中，y随x的增大而减小∴k−2<0∴k<2故选：D．在正比例函数y=ax中，当a<0时，y随x的增大而减小，据此判断即可．本题主要考查了正比例函数的性质，在正比例函数y=kx(k≠0)中，k>0，y随x的增大而增大，函数从左到右上升；k<0，y随x的增大而减小，函数从左到右下降．24. 解：A、y=−x2，当x>0时，y的值随x的值增大而减小，所以A选项错误；B、y=x−1，x>0时，y的值随x的值增大而增大，所以B选项正确；C、y=−x+1，当x>0时，y的值随x的值增大而减小，所以C选项错误；D、y=1x，当x>0时，y的值随x的值增大而减小，所以D选项错误．故选B．根据二次函数的性质对A进行判断；根据一次函数的性质对B、C进行判断；根据反比例函数性质对D进行判断．本题考查了二次函数的性质：二次函数y=ax2+bx+c(a≠0)的图象为抛物线；抛物线的顶点式为y=a(x−b2a)2+4ac−b24a ，对称轴为直线x=−b2a，顶点坐标为(−b2a,4ac−b24a)，当a>0，抛物线开口向上，在对称轴左侧，y随x的增大而减小，在对称轴右侧，y随x的增大而增大；抛物线与y轴的交点坐标为(0,c).也考查了一次函数和反比例函数的性质．25. 解：当x=1时，y=−12x=−12，∴A、C选项中的点均不在函数y=−12x的图象上；当x=2时，y=−12x=−1，∴B、选项中的点不在函数y=−12x的图象上；当x=−2时，y=−12x=1，∴D、选项中的点在函数y=−12x的图象上．故选D．分别将x=1、2、−2代入函数y=−12x求出y值，再对比四个选项中的点的坐标即可得出结论．本题考查了一次函数图象上点的坐标特征，逐一分析四个选项中点是否在一次函数图象上是解题的关键．26. 解：∵一次函数y=(4−m)x+m−2的图象经过第一，三，四象限，∴4−m>0且m−2<0，解得m<2．故答案是：m<2．根据一次函数图象与系数的关系得到4−m>0且m−2<0，然后求出两个不等式的公共部分即可．本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解：直线y=kx+b所在的位置与k、b 的符号有直接的关系.k>0时，直线必经过一、三象限.k<0时，直线必经过二、四象限.b>0时，直线与y轴正半轴相交.b=0时，直线过原点；b<0时，直线与y轴负半轴相交．27. 解：根据题意得{x−2≥0x−4≠0，解得x≥2且x≠4，∴自变量x的取值范围是x≥2且x≠4，故答案为x≥2且x≠4．根据分式和二次根式有意义的条件进行计算即可．本题考查了函数自变量的取值范围问题，掌握分式有意义的条件是分母不等于0，二次根式有意义的条件：被开方数大于等于0．28. 解：∵图象经过点(1,−1)，∴这个函数关系式可以是：y=x2−2x．故答案为：y=x2−2x．本题需先设出函数的关系式，再根据点的坐标即可得出结论．本题主要考查了二次函数图象上点的坐标特征，在解题时要能根据点的坐标写出函数关系式是本题的关键．29. 解：根据题意得：x−1≥0，解得：x≥1．故答案为：x≥1．因为当函数表达式是二次根式时，被开方数为非负数，所以x−1≥0，解不等式可求x的范围．此题主要考查函数自变量的取值范围，解决本题的关键是当函数表达式是二次根式时，被开方数为非负数．30. 解：∵一次函数y=2x+3中，k=2>0，∴y随x的增大而增大．故答案为：增大．根据一次函数的解析式判断出k的符号，进而可得出结论．本题考查的是一次函数的性质，熟知一次函数y=kx+b中，当k>0时，y随x的增大而增大是解答此题的关键．31. 解：∵点A的横坐标为3，∴y=−3+2=−1，∴点A的坐标为(3,−1)，∵一次函数的图象与直线y1=2x−1平行，∴设一次函数解析式为y=2x+b，∴2×3+b=−1，解得b=−7，∴一次函数解析式为y=2x−7．故答案为：y=2x−7．把点A的横坐标代入直线y2=−x+2求出点A的纵坐标，从而得到点A的坐标，然后根据互相平行的直线的解析式的k值相等设出一次函数解析式为y=2x+b，再把点A的坐标代入求出b的值，即可得解．本题考查了两直线相交或平行的问题，根据平行直线的解析式的k值相等设出一次函数的解析式是解题的关键．32. 解：∵函数y=kx+3的图象经过点(3,6)，∴6=3k+3，∴k=1．故答案为：1．将点(3,6)代入函数解析式中即可求出k值．本题考查了一次函数图象上点的坐标特征，牢记直线上任意一点的坐标都满足函数关系式y=kx+b是解题的关键．33. 解：将f(x)=1代入f(x)=x−2，可得：x−2=1，解得：x=3，故答案为：3将f(x)=1代入计算即可．本题主要考查的是一次函数问题，将f(x)=1代入是解题的关键．34. 解：∵函数y=(a+3)x+a2−9是正比例函数，∴a2−9=0，a+3≠0，解得：a=3．故答案为：3．由正比例函数的定义可得a2−9=0，a+3≠0，再解可得a的值．此题主要考查了正比例函数的定义，解题关键是掌握正比例函数的定义条件：正比例函数y=kx的定义条件是：k为常数且k≠0，自变量次数为1．35. 解：∵一次函数y=−2x+b(b为常数)的图象经过第二、三、四象限，∴k<0，b<0．故答案为：−1．根据一次函数的图象经过第二、三、四象限，可以得出k<0，b<0，随便写出一个小于0的b值即可．本题考查了一次函数图象与系数的关系，解题的关键是根据函数图象所过的象限找出它的系数的正负.本题属于基础题，难度不大，解决该题型题目时，能够熟练的运用一次函数图象与系数的关系是关键．36. 解：根据图象和数据可知，当kx+b>0时，即y>0，图象在x轴上面，此时x>1．故答案为：x>1．根据图象的性质，当y>0即图象在x轴上面，x>1．本题考查一次函数的图象，考查学生的分析能力和读图能力．37. 解：∵A点在直线y=2x上，∴3=2m，解得：m=3，2,3)，∴A点坐标为(32∵y=2x，y=ax+4，∴方程2x=ax+4的解即为两函数图象的交点横坐标，∴方程2x=ax+4的解为：x=3，2故答案为：3．2可先求得A点坐标，再结合函数图象可知方程的解即为两函数图象的交点横坐标，可求得方程的解．本题主要考查函数图象交点的意义，掌握函数图象的交点即为对应方程组的解是解题的关键．38. 解：∵一次函数y=kx+2k+3的图象不经过第三象限，k<0，∴{2k+3≥0≤k<0．解得：−32≤k<0．故答案为：−32由一次函数图象不过第三象限，利用一次函数图象与系数的关系即可得出关于k的一元一次不等式组，解之即可得出结论．本题考查了一次函数图象与系数的关系，根据函数图象不过第三象限，找出关于k的一元一次不等式组是解题的关键．39. 解：把x=0代入得y=2(0−1)+5=3，所以一次函数y=2(x−1)+5的图象在y轴上的截距为3．故答案为3．把x=0代入一次函数解析式求出对应的函数值，即可得到答案．本题考查了一次函数图象上点的坐标特征：一次函数y=kx+b(k、b为常数，k≠0)的图象上的点满足其解析式．40. 解：设一次函数的解析式为y=kx+b(k<0)，将A(2,4)代入y=kx+b，4=2k+b，∴b=4−2k．当k=−1时，b=4−2×(−1)=6．故答案为：y=−x+6．设一次函数的解析式为y=kx+b(k<0)，将点A的坐标代入其内即可得出b=4−2k，取k=−1，求出b值，此题得解．本题考查了一次函数的性质以及待定系数法求一次函数解析式，将点A的坐标代入一次函数解析式找出b=4−2k是解题的关键．。