化工原理 第三章 沉降与过滤

第三章沉降与过滤沉 降【 3-1 】 密度为 1030kg/m 3、直径为 400 m 的球形颗粒在 150℃的热空气中降落，求其沉降速度。

解 150℃时，空气密度0.835kg / m 3 ，黏度 2.41 10 5 Pa s颗粒密度p 1030kg / m3，直径 d p 4 10 4 m假设为过渡区，沉降速度为4 g 2 ( p)214 9 81 2 103013234u td p( . ) ( ) 4 101.79 m / s225225 2.41 10 50.835d p u t44101 79 0．835验算Re=.24 82 41 105..为过渡区3【 3-2 】密度为 2500kg/m 的玻璃球在 20℃的水中和空气中以相同的速度沉降。

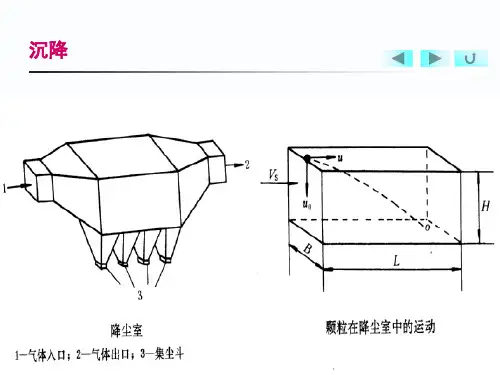
解 在斯托克斯区，沉降速度计算式为u td 2ppg / 18由此式得（下标w 表示水， a 表示空气）18pw d pw2( pa )d pa2 u t =gwad pw ( d pa(pa )wpw)a查得 20℃时水与空气的密度及黏度分别为w998 2 3w 1 . 004 10 3 . kg / m , Pa s 1 205 3a1 81 10 5 Pa sa . kg / m , .已知玻璃球的密度为p2500 kg / m 3 ，代入上式得dpw( 2500 1 205 ) 1 . 004 10.d pa( 2500998 2 1 . 81 10. )359.61【 3-3 】降尘室的长度为10m ，宽为 5m ，其中用隔板分为 20 层，间距为 100mm ，气体中悬浮的最小颗粒直径为10 m ，气体密度为1.1kg / m 3 ，黏度为 21.8 10 6 Pa s ，颗粒密度为4000kg/m 3。

试求： (1) 最小颗粒的沉降速度；(2) 若需要最小颗粒沉降，气体的最大流速不能超过多少m/s (3) 此降尘室每小时能处理多少m 3 的气体解 已知 d pc10 10 6 m, p4000kg / m 3 ,1.1kg / m 3 ,21.8 10 6 Pa s(1) 沉降速度计算假设为层流区gd pc 2 (p) 9 . 81 ( 10 10 6 2 ( 4000 1 1u t)6 . ) 0.01m / s1818 21.8 10d pc u t10 10 6 0 01 1 1000505． 2 验算 Re21 8 10 6 为层流.(2) 气体的最大流速 umax 。

第三章 沉降与过滤沉 降【3-1】 密度为1030kg/m 3、直径为400m μ的球形颗粒在150℃的热空气中降落，求其沉降速度。

解 150℃时，空气密度./30835kg mρ=，黏度.524110Pa sμ-=⨯⋅颗粒密度/31030p kg m ρ=，直径4410p d m -=⨯ 假设为过渡区，沉降速度为()(.)()./..1122223345449811030410179225225241100835p t p g u d m s ρρμρ--⎡⎤-⎡⎤⨯==⨯⨯=⎢⎥⎢⎥⨯⨯⨯⎢⎥⎣⎦⎣⎦验算.R e ..454101790．835=24824110p t d u ρμ--⨯⨯⨯==⨯为过渡区【3-2】密度为2500kg/m 3的玻璃球在20℃的水中和空气中以相同的速度沉降。

试求在这两种介质中沉降的颗粒直径的比值，假设沉降处于斯托克斯定律区。

解 在斯托克斯区，沉降速度计算式为()/218t p p u d g ρρμ=-由此式得（下标w 表示水，a 表示空气）()()2218=pw p wp a pat wad d u gρρρρμμ--=pw pad d =查得20℃时水与空气的密度及黏度分别为./,.339982 100410w w kg m Pa s ρμ-==⨯⋅./,.35120518110a a kg m Pa s ρμ-==⨯⋅已知玻璃球的密度为/32500p kg m ρ=，代入上式得.961pw pad d =【3-3】降尘室的长度为10m ，宽为5m ，其中用隔板分为20层，间距为100mm ，气体中悬浮的最小颗粒直径为10m μ，气体密度为./311kg m ，黏度为.621810Pa s -⨯⋅，颗粒密度为4000kg/m 3。

试求：(1)最小颗粒的沉降速度；(2)若需要最小颗粒沉降，气体的最大流速不能超过多少m/s? (3)此降尘室每小时能处理多少m 3的气体？解 已知,/./.6336101040001121810p c p d m k g m k g m P a sρρμ--=⨯===⨯⋅,, (1) 沉降速度计算 假设为层流区().()(.)./.26269811010400011001181821810p c p t gd u m sρρμ---⨯⨯-===⨯⨯验算..R e.66101000111000505221810pc t d u ρμ--⨯⨯⨯===<⨯． 为层流(2) 气体的最大流速m ax u 。

第三章沉降与过滤本章重点：重力沉降及恒压过滤第一节概述3-1非均相物系的分离混合物：均相混合物(物系)：物系内部各处物料性质均匀，无相界面。

例：混合气体、溶液。

非均相混合物(物系)：物系内部有隔开的相界面存在，而在相界面两侧的物料性质截然不同的物系。

例：含尘气体、悬浮液、乳浊液、泡沫液。

许多化工生产过程中，要求分离非均相物系。

含尘和含雾的气体，属于气态非均相物系。

悬浮液、乳浊液及泡沫液等属于液态非均相物系。

非均相物系◆分散相(分散物质)：处于分散状态的物质。

气体中尘粒、悬浮液中的颗粒、乳浊液中的液滴。

◆连续相(分散介质)：包围着分散相，处于连续状态的物质。

含尘气体中的气体、悬浮液中的液体。

均相混合物：吸收、蒸馏。

非均相混合物：分散相、连续相物理性质不同(ρ不同)→机械方法：沉降、过滤。

非均相物系分离的目的：（1）回收分散物质（2）净制分散介质本章将简要地介绍重力沉降、离心沉降及过滤等分离法的操作原理及设备。

第二节重力沉降沉降(settling)：在某种力(重力、离心力)作用下，利用连续相与分散相的密度差异，使之发生相对运动而分离的操作。

重力沉降：由地球引力(重力)作用而发生的沉降过程。

3-2颗粒与流体相对运动时所受的阻力球形颗粒的自由沉降自由沉降：单个颗粒在流体中沉降，或者颗粒群在流体中充分地分散颗粒之间互不接触互不碰撞的条件下的沉降。

将表面光滑、刚性的球形颗粒置于静止的流体中。

颗粒：ρP 、d P 、m 流体：ρ、μ、ρP ＞ρ颗粒与流体的的相对运动速度(相对于流体的降落速度)：u颗粒在流体中作重力沉降或离心沉降时，要受到流体的阻力作用,通常称为曳力（drag force ）或阻力。

F d分析颗粒受力情况：ζ：阻力系数，无量纲，实验测定。

ζ：量纲分析因次分析：ζ=f(Re)， 对于球形颗粒实验结果：10-4＜Re ≤2 层流区 ζ=24/ Re →斯托克斯区2＜Re ≤500 过渡区→艾伦区 500＜Re ≤2×105 湍流区 ζ=0.44 →牛顿区浮 图3－1 颗粒受力图dtdu ma u d g d g d F F mg F P P P P d==⋅⋅⋅-⋅⋅-⋅⋅=--=∑24161612233ρπζρπρπ浮μρ⋅⋅=u d P Re Re10=ζ3-3 沉降速度一、沉降速度(u t )的计算∑F 右边前两项与u 无关，mg 、F 浮→const ，第三项随u 增大而增大，F d ∝ u 2/2。

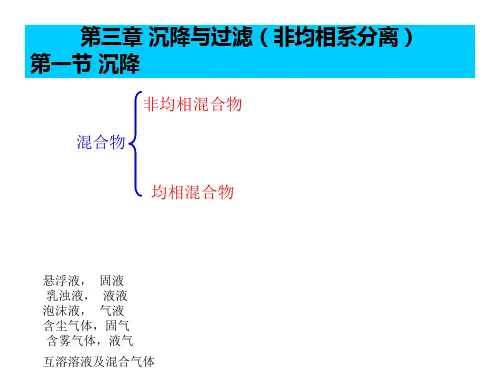
1掌握重力沉降的基本原理、典型设备及应用；了解过滤的基本操作过程、典型的设备，熟练掌握恒压过滤的操作及计算；第三章 非均相物系分离2非均相混合物的概念：相界面、混合物分类：固体非均相、气体非均相和液体非均相混合物 基本概念：分散相和连续相目的：获得产品，回收再利用，环保的需求等方法：主要的物理分离方法是沉降与过滤3一、沉降速度3.1 重力沉降F b F dF g 颗粒受力分析：以球形颗粒为研究对象重力： 流体对颗粒的浮力：颗粒运动后流体对颗粒的阻力：仿照管内流体流动阻力的计算gd F p p g r p 36 1= gd F p b r p 36 1 = 22u A F P d r x =4当 时，u ＝u t ，则： td du m F F F F d b g = - - = t r pr p x r p r p d du d u d g d g d p p p p p p 32 23 36 2 4 6 6 = - - 由动量定理： 颗粒在流体内作重力沉降运动的过程将经历先加速后匀速 的运动，其最终的速度称重力沉降速度，且颗粒的加速运 动过程很短，一般情况下不予考虑。

2 4 6 6 2 23 3 = - - tp p p p u d g d g d r p x r p r p rxr r 3 )( 4 - = p p t gd u 整理得 0 = t d du5÷ ÷ øö ç ç è æ = μ u ρ d R p e 球形颗粒的阻力系数ξ是颗粒雷诺数 的函 数，教材P89页的ξ与Re 的关系曲线是由球形颗粒做实验得出 的。

(1) 层流区：10 ­4 ＜Re ＜1，e R 24 = x (2) 过渡区：1＜Re ＜10 3 ， 6 . 0 5 . 18 eR = x (3) 湍流区：10 3 ＜Re ＜2×10 5 ， 曲线分三个区：44. 0 = x6ξ7将用沉降速度u t 表示的颗粒雷诺数Re 代入层流区沉降速度公式中：m rt p et u d R = eR 24 = x mr r 18 ) ( 2gd u p p t - = 即层流区沉降速度计算式，也称斯托克斯（Stokes ）公式，用于计算颗粒在流体中作自由沉降运 动的层流沉降速度计算式。

第三章 颗粒流体力学基础与机械分离教学内容（8学时）：1. 流体与单个固体颗粒的相对运动、沉降速度，2. 重力沉降、离心沉降原理与设备，3. 过滤、过滤速率及其在恒压条件下的应用 基本要求：1. 理解：流体与单个固体颗粒的相对运动，2. 掌握：重力沉降室的沉降条件及生产能力；旋风除尘器分离能力的估算，3. 理解：过滤基本原理，过滤速率、过滤推动力的意义，掌握：恒压过滤的计算，了解过滤设备3-1 概述化工生产中，需要将混合物分离的情况很多。

如：原料的分离与纯化；产品的分离与纯化；生产中的废气、废液等在排放前都应将其中所含有的有害物质尽量除去。

大致来说，混合物可分为两大类：混合气体溶液如且不存在相界面的物系物系内部各处物性均匀均相物系),(:,:NaOH连续物质所组成的物系有相界面的分散物质和如具有不同物理性质非均相物系)(:ρ均相为互溶物系。

非均相为不互溶物系。

其中，非均相混合物包括⎩⎨⎧液态非均相气态非均相 由⎩⎨⎧悬浮、乳浊、泡沫液等连续物质含雾气体如含尘气体分散物质:,:非均相物系分离法一般用机械分离法，使分散相与连续相发生相对运动，从而分离。

均相物系分离法将在传热和传质有关章节中讲。

⎪⎩⎪⎨⎧流体相对于颗粒的运动过滤离心沉降过程颗粒相对于流体的运动重力沉降机械分离方法::惯性离心力还包括重力以压力差为主过滤作用力速度快还有重力以惯性离心力为主离心沉降作用力速度慢以重力为主重力沉降作用力,,:,,:,:重力沉降及离心沉降可用于分离气态及液态非均相；过滤多用于液态非均相，包括加压，减压，常压及离心过滤。

3-2 筛分1、固体颗粒的大小颗粒最基本的特性是其形状和大小(粒度)，形状均匀的为球形。

颗粒的大小可按其直径的大小来表示，粗的可用mm表示，细的可用标准筛的筛孔号数来表示，再细的则以μm来度量。

测量颗粒大小的最简易的方法是用筛。

标准筛为包括一系列具有不同大小孔眼的筛，若一种颗粒能通过某一号筛而截留于相邻的另一号孔眼较小的筛上，则此颗粒的直径一般认为等于此两号筛孔的宽度的平均值。