下载文档原格式
§7.4 一阶线性微分方程教学内容：一．一阶线性微分方程一阶线性微分方程的标准形式为()()y P x y Q x '+=，其中()()P x Q x ,为已知连续函数，()Q x 称为方程的自由项.当()0Q x ≠时,称()()y P x y Q x '+=为一阶线性非齐次微分方程.当()0Q x =时,称()0y P x y '+=为()()y P x y Q x '+=所对应的一阶线性齐次微分方程．1. 一阶齐次线性微分方程一阶齐次线性微分方程()0y P x y '+=是可分离变量的微分方程，通解为()d e P x x y C -⎰=．注 对于一阶线性齐次微分方程()0y P x y '+=的求解有两种常用方法：（1）利用分离变量法求其通解；（2）利用通解公式法求其通解.先化为标准形式确定()P x ，再代入通解公式求解．2.一阶非齐次线性微分方程()()y P x y Q x '+=的通解为()()d ()d ()e d e P x x P x x y Q x x C -⎰⎰=+⎰（常数变易法）.注：对于一阶非齐次线性微分方程()()y p x y Q x '+=的求解有两种常用方法：（1）先求出对应的齐次方程通解，再利用常数变易法求其通解.（2）直接利用非齐次方程的通解公式求其通解.二．伯努利方程1．形如d ()()(0,1)d n y P x y Q x y n x +=≠的方程为伯努利方程.2．伯努利方程的解法：令1n z y -=，可化成关于z 为未知函数的一阶线性微分方程d (1)()(1)()d z n P x z n Q x x+-=-，解出z 后代入变换关系1n z y -=即得方程原方程的通解.三．例题讲解例1.求微分方程e sin 0y y x -'-=的通解.例2.求2d (21)d y x y x=-的通解． 例3.求20y xy '-=满足03x y ==的特解．例4．医学研究发现，刀割伤口表面恢复的速度为()2d 51d =-≥y t t t （2cm /day ），其中，y 表示伤口 的面积，t 表示时间，假设215cm t y ==，问受伤5天后该病人的伤口表面积为多少.例5．求微分方程)ln ln 1(x y y y x -+='的通解.例6.求方程30xy y x '=>（）的通解. 例7.求方程23(0)xy x y x '=+>的通解．例8.求一阶线性微分方程230xy x y x '=+>（）满足初始条件12x y ==的特解．例9.已知汽艇在静水中行驶时受到的阻力与汽艇的行驶速度成正比，若一汽艇以10km/h 的速度在静水中行驶时关闭了发动机，经20s 后汽艇的速度减至6km /h ，试确定发动机停止2min 后汽艇的速度. 例10.求解微分方程2d (ln )(0)d y y x y x x x+=>.。
同济大学高等数学上册第七章常微分方程同济大学高等数学上册是大多数理工科专业的学生必修的课程，第七章是关于常微分方程的内容。
常微分方程是数学中的一个重要分支，广泛应用于物理、化学、经济等领域。
掌握常微分方程的基本理论和解法对于理解和应用这些领域的知识具有重要意义。
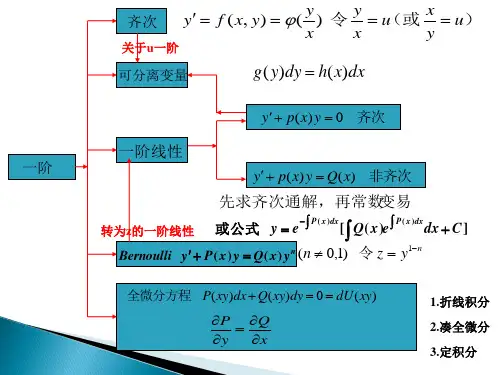
本章内容主要包括：一阶常微分方程、高阶常微分方程、一阶线性微分方程、可分离变量的微分方程、齐次线性微分方程和一阶齐次线性方程、一阶齐次线性非齐次方程、二阶常系数齐次线性方程、常系数非齐次方程等。
一、一阶常微分方程一阶常微分方程是指未知函数的导数只包含一阶导数的方程。
例如，dy/dx = f(x)。
常微分方程的求解可以采用分离变量法、恰当方程、公式法等。
其中分离变量法是常用的解法之一。
分离变量法的基本思想是将方程两边的变量分离开来，从而达到求解的目的。
二、高阶常微分方程高阶常微分方程是未知函数的导数包含高于一阶导数的方程。
例如，d²y/dx² + p(x) dy/dx + q(x) y = f(x)。
高阶常微分方程的求解可以采用常系数线性微分方程的方法。
常系数线性微分方程是指系数为常数的微分方程，其求解方法相对简单。
三、一阶线性微分方程一阶线性微分方程是指未知函数的导数与未知函数本身之间线性相关的方程。
例如，dy/dx + p(x) y = q(x)。
一阶线性微分方程的求解可以借助于积分因子的方法。
积分因子的选择是使方程两边的未知函数系数相等，从而将方程转化为可积分的形式。
四、可分离变量的微分方程可分离变量的微分方程是指未知函数和自变量可以在方程中分离的方程。
例如，dy/dx = f(x)/g(y)。
可分离变量的微分方程的求解可以通过对方程两边的变量分离，然后进行适当的积分得到。
这种方法常用于求解一些特殊形式的微分方程。
五、齐次线性微分方程和一阶齐次线性方程齐次线性微分方程是指未知函数的导数和未知函数本身之间构成齐次线性关系的微分方程。
