大学本科理论力学课程动力学例题

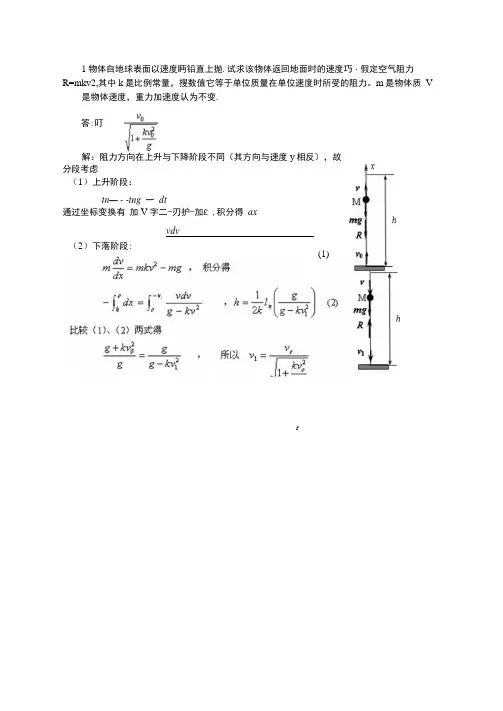
1物体自地球表面以速度眄铅直上抛.试求该物体返回地面时的速度巧・假定空气阻力R=mkv2,其中k是比例常量，搜数值它等于单位质量在单位速度时所受的阻力。

m是物体质V 是物体速度，重力加速度认为不变.答:叮解：阻力方向在上升与下降阶段不同（其方向与速度y相反），故分段考虑（1）上升阶段：tn— - -tng一dt通过坐标变换有加V字二-刃护-加£ ,积分得axvdv（2）下落阶段:(1)g2.静止中心0以引力F=k2mr吸弓I质量是m的质点M,其中k是比例常量，r=OM是点M的矢径.运动开始时OMo=b,初速度时呵并与阪成夹角求质点M的运动方程。

x = b cos 处 + —cosasin ktky = —sinasin^k解：取坐标如图，质点M在任意位貳将fna = F 沿x、y轴投彫，得mx = 一F cos<p= -k2fnrcos （p= -Qmxfny = 一Fsin cp= -k2fnr sin (p= -k^my艮卩x+k2x = 0 , y+^2y = 0徽分方程得通解为：x = s coskt+c2 sin kt求导得x = -kc x sin kt + kc2 coskt , y = -kc3 sin kt + kc^ cos kt (2)已知初始条件f=0 z 妒b z /o=0，x0 = v0 sin a ,代入方程（1），（2）得点M的运动方程为v =—cosax = 2?cos Ar/ +—kcos ar sin kt -I sin asin kt y =c3 cos kt + c^ sin kt (1)九=v0 sin a3单摆M 的悬线长/,摆重G 支点B 具有水平向左的均加速度a.如将摆在&=0处静止 释啟，试确定悬线的张力T （表示成&的函数）.解：质点的相对徴分方程为 ma r = mg+f +©投影到法线方向由式(2)得T = Gsin3 + —acos0 + — v 2g 0T = G 3 sin + 3 — cos — 2 —\ g S )答・ T - G(3sin3-cos^- 2-) g g投影到切线方向= T-Gsin^-0e cosB g !(2)由式（1）得 妙=gcos^-usin 0分离变量并积分|*V Xiv = \ f geos^10- [ asm Odd v 2 = 2"gsin &+ocos&-a 1(3)将式（3）代入上式代入式（2）得dt dt积分得4.水平面内弯成任意形状的细管以匀角速度G 绕点0转动.光滑小球M 在管內可自由 运动.设初瞬时小球在吆处，OMo=©相对初速^v o =0,求小球相对速度大小冬与极径r的关系。

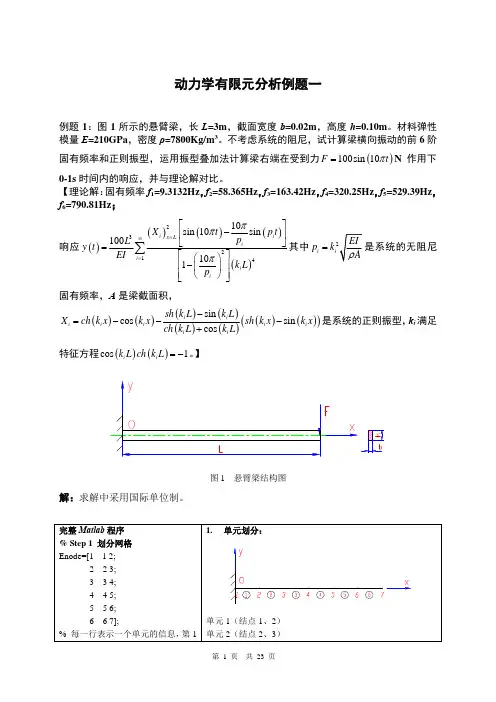
动力学有限元分析例题一例题1：图1所示的悬臂梁，长L =3m ，截面宽度b =0.02m ，高度h =0.10m 。

材料弹性模量E =210GPa ，密度ρ=7800Kg/m 3。

不考虑系统的阻尼，试计算梁横向振动的前6阶固有频率和正则振型，运用振型叠加法计算梁右端在受到力(100sin 10F t )π=N 作用下0-1s 时间内的响应，并与理论解对比。

【理论解：固有频率f 1=9.3132Hz ，f 2=58.365Hz ，f 3=163.42Hz ，f 4=320.25Hz ，f 5=529.39Hz ，f 6=790.81Hz ；响应()()()()()2321410sin 10sin 100101i i x L i i i i X t p p L y t EI k L p πππ=∞=⎡⎤−⎢⎥⎣t =⎡⎤⎛⎞⎢⎥−⎜⎟⎢⎥⎝⎠⎣⎦∑⎦其中i i p k =是系统的无阻尼固有频率，A 是梁截面积，()()()()()()()()(sin cos sin cos i i i i i i i i i sh k L k L )X ch k x k x sh k x k x ch k L k L −=−−−+是系统的正则振型，k i 满足特征方程()()cos 1i i k L ch k L =−。

】图1 悬臂梁结构图解：求解中采用国际单位制。

Edb=extract(Edof,Egv(:,i));ext=ex+(i-4)*4;eldraw2(ext,eyt,[2 3 1]);eldisp2(ext,eyt,Edb,[1 2 2],magnfac);FreqText=num2str(Freq(i));text(4*(i-4)+1.25,-3.0,FreqText);end% 绘制前6阶正则振型图。

% Step 6 设定简谐响应分析条件和6.进入简谐响应分析，给定相关参数选取模态T=1; nev=2;% 设定计算总时间为1s，选择结构的前两阶模态作为振型叠加法分析的基础。

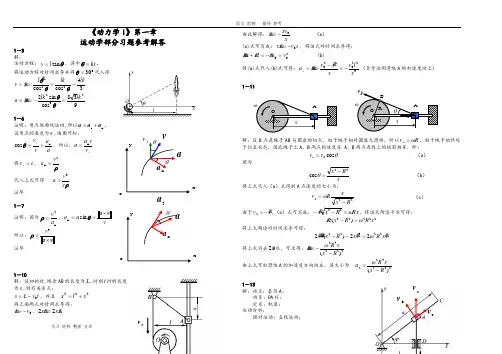
学习 资料 整理 分享《动力学I 》第一章 运动学部分习题参考解答1－3 解：运动方程：θtan l y =，其中kt =θ。

将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l y v ====θθθ 938cos sin 2232lk lk y a =-==θθ1－6证明：质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a v v yn cos ==θ，所以: yv va a n =将c v y =，ρ2n v a =代入上式可得 ρc v a 3=证毕 1－7证明：因为n2a v =ρ，v a a v a ⨯==θsin n所以：va ⨯=3v ρ证毕1－10解：设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式：t v L s 0-=，并且 222x l s +=将上面两式对时间求导得： 0v s-= ，x x s s 22= 由此解得：xsv x-= （a ） (a)式可写成：s v x x 0-= ，将该式对时间求导得： 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得：3220220xlv x x v x a x -=-==（负号说明滑块A 的加速度向上）1－11解：设B 点是绳子AB 与圆盘的切点，由于绳子相对圆盘无滑动，所以R v B ω=，由于绳子始终处于拉直状态，因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等，即： θcos A B v v = （a ） 因为xR x 22cos -=θ （b ） 将上式代入（a ）式得到A 点速度的大小为： 22Rx x Rv A -=ω （c ）由于x v A -=，（c ）式可写成：Rx R x xω=--22 ，将该式两边平方可得： 222222)(x R R x xω=- 将上式两边对时间求导可得：x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后，可求得：22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左，其大小为 22242)(R xxR a A -=ω1－13解：动点：套筒A ；动系：OA 杆； 定系：机座； 运动分析：绝对运动：直线运动；o vo va ve vr vxovxot学习 资料 整理 分享 相对运动：直线运动； 牵连运动：定轴转动。

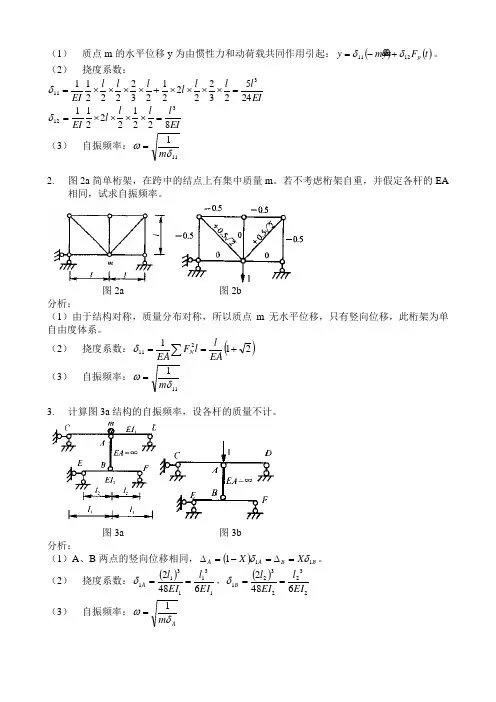
典型例题分析（动力学）一、自由度1.判断自由度的数量。

二、单自由度体系的自振频率1. 试列出图1a结构的振动方程，并求出自振频率。

EI＝常数。

图1a 图1b M1 图1c M2分析：（1） 质点m 的水平位移y 为由惯性力和动荷载共同作用引起：()()t F ym y p 1211δδ+-= 。

（2） 挠度系数：EIll l l l l l EI 245232222123222211311=⨯⨯⨯⨯+⨯⨯⨯⨯=δEIll l l EI 822122211312=⨯⨯⨯⨯=δ（3） 自振频率：111δωm =2.图2a 简单桁架，在跨中的结点上有集中质量m 。

若不考虑桁架自重，并假定各杆的EA 相同，试求自振频率。

图2a 图2b分析：（1）由于结构对称，质量分布对称，所以质点m 无水平位移，只有竖向位移，此桁架为单自由度体系。

（2） 挠度系数：()211211+==∑EAl l F EAN δ（3） 自振频率：111δωm =3.计算图3a 结构的自振频率，设各杆的质量不计。

图3a 图3b分析：（1）A 、B 两点的竖向位移相同，()B B A A X X 111δδ=∆=-=∆。

（2） 挠度系数：()13113116482EI l EI l A ==δ，()23223216482EI l EI l B ==δ（3） 自振频率：Am δω1=三、单自由度体系的动力特性 1. 简支梁，跨度a ，抗弯刚度EI ，抗弯截面模量W z 。

跨中放置重量为G 转速n 的电动机．离心力竖直分量()tF t F p p θsin =。

若不计梁重，试求动力系数、最大动位移及最大动应力。

分析：（1）动力系数：211⎪⎭⎫ ⎝⎛-=ωθμEIGag n st st48303=∆∆==ωπθ（2） 最大动位移：EI aF y y y y p st st st st d 4831111max max ==∆+=∆+=δδμ（3） 最大动应力： ()a G F MM MM MW MpGstGd z+=+=+==μμσ41maxmaxmaxmax四、两个自由度体系的特性（自振频率、主振型、位移－振型分解法） 1. 求1a 体系的自振频率和主振型，作振型图并求质点的位移。

动力学第三章部分习题解答3－3 取套筒B 为动点，OA 杆为动系 根据点的复合运动速度合成定理r e a v v v +=可得：l v v ω==e 0a 30cos ，l v v v BC B ω332a === 研究AD 杆，应用速度投影定理有：030cos D A v v =，l v D ω334=再取套筒D 为动点，BC 杆为动系，根据点的复合运动速度合成定理r D BC D v v v +=将上式在x 轴上投影有：r D BC D v v v +-=-，l v v v BC D D ω332r =+-=3－4 AB 构件（灰色物体）作平面运动， 已知A 点的速度s A O v A /0cm 4510==ωAB 的速度瞬心位于C ，应用速度瞬心法有：rad/s 23==AC v A AB ω BC v AB B ω=，设OB 杆的角速度为ω，则有rad/s 415==OB v B ω 设P 点是AB 构件上与齿轮I 的接触点， 该点的速度：CP v AB P ω=齿轮I 的角速度为：rad/s 61==r v PI ω a v e vr vA vDv rD v A vB P v CAB ωI ω3－6 AB 杆作平面运动，取A 为基点 根据基点法公式有：BA A B v v v +=将上式在AB 连线上投影，可得0,01==B O B v ω因此，041ωω==AB v A AB因为B 点作圆周运动，此时速度为零，因此只有切向加速度（方向如图）。

根据加速度基点法公式n t BA BAA B aaa a ++=将上式在AB 连线上投影，可得n060cos BA A B a a a +=-，r a B 205.2ω-=201231ωα-==B O a B B O （瞬时针）3－7 齿轮II 作平面运动，取A 为基点有nt BA BA A B a a a a ++= n t 1BA BA a a a a ++=将上式在x 投影有：n 1cos BA a a a -=-β由此求得：212n 2cos 2r a a r a BAII βω+==再将基点法公式在y 轴上投影有：2t2sin r a a II BA αβ==，由此求得22sin r a II βα=再研究齿轮II 上的圆心，取A 为基点n t n t2222A O AO A O O aaa aa++=+将上式在y 轴上投影有2sin 2t t 22βαa r a a II AO O ===， B vBAv A vAa Ba t BA an BA atBA anBA axyt2A Oa n 2AO a xyn 2O a t 2Oa由此解得：)(2sin 2121t 221r r a r r a OO O +=+=βα再将基点法公式在x 轴上投影有：n1n22A O O a a a -=- 由此解得：2cos 1n2a a a O -=β，又因为221n 212)(O O O r r a ω+= 由此可得：)(2cos 21121r r a a O O +-±=βω3－9 卷筒作平面运动，C 为速度瞬心， 其上D 点的速度为v ，卷筒的角速度为r R vDC v -==ω 角加速度为rR ar R v -=-== ωα 卷筒O 点的速度为：rR vRR v O -==ω O 点作直线运动，其加速度为 rR aRr R R v va O O -=-==研究卷筒，取O 为基点，求B 点的加速度。

理论力学（动力学专题）_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.在图示系统中，已知：匀质圆柱A的质量为m1，半径为r，板B的质量为m2，F为常力，圆柱A在板面上作纯滚动，板B沿光滑水平面运动。

试求：（1）以x和φ为广义坐标，用第二类拉格朗日方程建立系统的运动微分方程；（2）圆柱A的角加速度和板B的加速度。

答案:2.图示质量为m的小球M放在半径为r的光滑圆管内，并可沿管滑动。

如圆管在水平面内以匀角速度ω绕管上某定点A转动，试求小球沿圆管的运动微分方程。

答案:3.匀质杆AB的质量m=10kg ，长l=4m ，在光滑的水平面内运动，其质心速度v C=20m/s，方向垂直于A，角速度ω=10rad/s ，转向如图示。

当杆的A 端突然固定时，试求：(1)杆的角速度；(2) 杆端A的碰撞冲量。

答案:ω2=10 rad/sI=04.图示物块A的质量为m，均质杆OB的质量为1.5m，长为l，上、下两弹簧的刚度系数分别为2k与k。

在平衡位置时，弹簧处于铅垂，而杆OB处于水平。

试求系统的主振动频率。

若给杆以微小的起始角速度ω0时，物块A 的速度等于零，求物块A的运动方程。

答案:5.重P1为180N的矩形框架绕水平轴AB以角速度2πrad/s 转动；框架的C，D上又安装重P2为120N的飞轮M，如图所示。

飞轮的转速为n=1800r/min，飞轮对自转轴的回转半径ρ=100 mm，CD=300 mm，AB=600 mm。

求：(l)在轴承C与D上的陀螺力；(2)轴承A和B上的全压力；(3)欲使轴承A上的压力为零时，飞轮的自转角速度。

答案:F C=F D=483.4N；F A=91.7N, F B=391.6N；ω=117rad/s6.长为l、单位长度质量为ρ的链条，从板上小孔向下降落。

最初，当y很小时，链条处于静止，并不计摩擦。

在图a中，假设链条在通过小孔前都是静止的；在图b 中，假设任何时刻链条各节都具有相同的速度值。

1.在图示平面机构中，菱形板分别与杆AA1和BB 1铰接，两杆可分别绕轴A 1 和轴B 1作定轴转动。

AB =BD =20cm ，AA 1=25cm 。

当ϕ=30°，AA 1⊥BB 1时，设平板的角速度ω=2rad/s 。

试求此瞬时点D 的速度和杆AA 1的角速度。

解：菱形板的速度瞬心在P 点，故s cm /2030sin =⋅︒⋅=⋅=ωωAB AP v A杆AA 1的角速度 s rad/8.0AA 11==Av ω（顺钟向）D 点的速度 s cm/720=⋅=ωDP v D（斜向左下方）2.等腰三角形平板ABC 的腰长AB =BC ＝5 cm ，AC =6 cm ，端点A 和端点B 分别在水平面上和斜面上运动。

斜面与铅垂线之间的夹角ϕ＝⎪⎭⎫ ⎝⎛43arctan 。

在图示位置时，AC 边铅垂，平板的角速度ω＝4 rad/s ，角加速度α＝5 rad/s 2。

试求该瞬时A ，B 和C 三点的加速度的大小。

解：平板取A 为基点 t n BA BA A B a a a a +==式中2n ωAB a BA =，αAB a BA =tBC ： ()()ϕθϕθϕ---+=cos sin cos 0t n BA BA A a a a故 2cm /s 1.2=A ay ： ϕϕϕcos sin cos t n BA BA B a a a --=-故 2cm/s 85=B a取A 为基点 t n CA CA A C a a a a ++=式中 2n ωAC a CA =，αAC a CA =tx ：2t cm/s 9.27=+-=CA A C a a a xy ： 2n cm/s 96-=-=CA C a a y 2cm/s 100=C a3.在图示平面机构中，已知：杆OA 以匀角速度0ω绕定轴O 转动，OA =AC =r ，O 1B =2r ， β=30°。

在图示位置时，OA ，CB 水平，O 1B ，AC 铅垂。

《动力学 I 》第一章运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。

将运动方程对时间求导并将 030=θ代入得34cos cos 22lk lk l y v ====θθθ98cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动 , 所以 n t a a a +=, 设质点的速度为 v , 由图可知 : a a vv y n cos ==θ,所以 : yv va a n = 将c v y =, ρ2n va =代入上式可得ρc v a 3=证毕 1-7证明:因为 n2a v=ρ, va a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时 , 绳索 AB 的长度为 L , 时刻 t 时的长度为 s , 则有关系式: t v L s 0-=,并且 222x l s +=将上面两式对时间求导得:0v s-= , x x s s 22= 由此解得:xsv x-= (a (a式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x=-=+ (b 将 (a式代入 (b式可得:3220220xlv x x v x a x -=-==(负号说明滑块 A 的加速度向上1-11解:设 B 点是绳子 AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上 A 、 B 两点的速度在 A、 B 两点连线上的投影相等,即: θcos A B v v = (a 因为xR x 22cos -=θ (b 将上式代入(a 式得到 A 点速度的大小为: 22Rx x Rv A -=ω (c由于 x v A -=, (c 式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222 (x R R x x ω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222 (2ω=-- 将上式消去 x 2后,可求得:22242(R x xR x--=ω由上式可知滑块 A 的加速度方向向左,其大小为 2 2242(R x xR a A -=ω1-13解:动点:套筒 A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。

《理论力学》章节典型例题（含详解）A 卷1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内，载荷如图所示。

其中转矩M=20kN.m ，拉力F=400kN,分布力q=20kN/m,长度l=1m 。

试求固定端A 的约束力。

解：取T 型刚架为受力对象，画受力图.1-2 如图所示，飞机机翼上安装一台发动机，作用在机翼OA 上的气动力按梯形分布：1q =60kN/m ，2q =40kN/m ，机翼重1p =45kN ，发动机重2p =20kN ，发动机螺旋桨的反作用力偶矩M=18kN.m 。

求机翼处于平衡状态时，机翼根部固定端O 所受的力。

解：1-3图示构件由直角弯杆EBD以及直杆AB组成，不计各杆自重，已知q=10kN/m，F=50kN，M=6kN.m，各尺寸如图。

求固定端A处及支座C的约束力。

1-4 已知：如图所示结构，a, M=Fa, 12F F F ==, 求：A ，D 处约束力.解：1-5、平面桁架受力如图所示。

ABC 为等边三角形，且AD=DB 。

求杆CD 的内力。

1-6、如图所示的平面桁架，A 端采用铰链约束，B 端采用滚动支座约束，各杆件长度为1m 。

在节点E 和G 上分别作用载荷E F =10kN ，G F =7 kN 。

试计算杆1、2和3的内力。

解：2-1 图示空间力系由6根桁架构成。

在节点A上作用力F，此力在矩形ABDC平面内，且与铅直线成45º角。

ΔEAK=ΔFBM。

等腰三角形EAK，FBM和NDB在顶点A，B和D处均为直角，又EC=CK=FD=DM。

若F=10kN，求各杆的内力。

2-2 杆系由铰链连接，位于正方形的边和对角线上，如图所示。

在节点D沿对角线LD方向F。

在节点C沿CH边铅直向下作用力F。

如铰链B，L和H是固定的，杆重不计，作用力D求各杆的内力。

2-3 重为1P ＝980 N ，半径为r =100mm 的滚子A 与重为2P ＝490 N 的板B 由通过定滑轮C 的柔绳相连。