中国精算师《寿险精算》章节题库-生存年金的精算现值(圣才出品)

第13章寿险定价概述1．简述寿险定价的基本原则。

答：寿险定价的基本原则包括：（l）充足性原则该原则是审慎的精算原理和法律要求的首要原则。

它是指保险费率应高至足以弥补预计发生的各项赔付以及有关的费用。

如果费率不充足，就会导致保险人难以仅依赖收取的保险费来履行未来保险赔付的义务，进而影响保险人的盈利能力和偿付能力，最终可能使被保险人的利益受到损害。

因此寿险产品的费率不能太低。

（2）合理性原则该原则是指寿险产品的平均费率水平应该和预计发生的各项赔付及费用水平相匹配，保险人获得一个恰当的利润水平。

（3）公平性原则。

该原则是指保险人对被保险人所承担的保险保障和赔付责任应该和投保人所缴纳的保费对等。

公平性原则是针对每个被保险人而言，合理性原则只针对某个险种的平均费率水平而言。

（4）可行性原则每一个寿险产品在开发和定价时都有其预定的目标客户群，费率的厘定不仅仅要考虑赔付的需要，以及合理性、公平性的原则，还要考虑目标客户群的特征以及其缴纳保费的能力，这样才能提高行销的可行性。

（5）稳定性原则该原则是指保险费率在短期内应该是相对稳定的，这样既有利于保险经营，又有利于投保人续保。

（6）弹性原则该原则是指保险费率要随着实际情况的变化而有所变化。

2．了解寿险公司产品开发的过程。

答：险种开发流程。

可分为以下几个环节：（1）产品形态构思。

新产品形态的思路来源包括由销售渠道提供的根据客户或销售人员对现有产品的反馈、经验分析的结果、同业产品的启发、政策法规的导向等。

（2）产品可行性分析。

它是新产品开发项目前期的重要工作，其分析结果将被写入产品可行性分析报告以供公司管理层决策参考。

产品可行性分析报告主要分析该产品能否符合公司策略、适应客户需求、合法合规、符合内部运营和系统支持能力、符合公司产品盈利性标准、投入产出合理性，并对产品的主要风险点进行提示。

（3）管理层审批。

由于寿险产品的长期性，每一个新产品的上市，保险公司都必须在系统中记录相关信息，提供相应的服务，长达数年甚至上百年，因而保险公司对于新产品开发的决策通常比较谨慎。

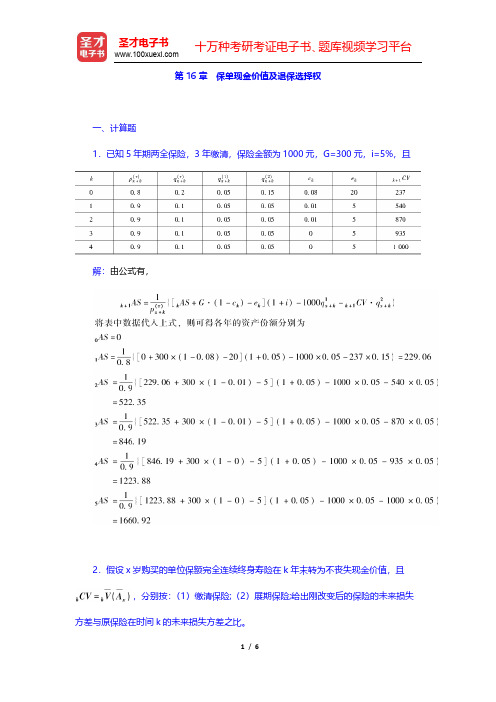
第16章保单现金价值及退保选择权一、计算题1．已知5年期两全保险，3年缴清，保险金额为1000元，G=300元，i=5%，且解：由公式有，2．假设x岁购买的单位保额完全连续终身寿险在k年末转为不丧失现金价值，且，分别按：（1）缴清保险;（2）展期保险;给出刚改变后的保险的未来损失方差与原保险在时间k的未来损失方差之比。

解：原保险在时间k的未来损失为：对上式两边取方差，可得原保险在时间k的未来损失方差为：（1）用b k表示在时刻k的缴清保险的保险金额，则，在k年末改为缴清保险后，其未来损失为：其中k CV为常数。

对上式两边取方差，可得改为缴清保险后，在时间k的未来损失方差为：所以，改为缴清保险后的未来损失方差与原保险在时间k的未来损失方差之比为：（2）用s表示购买展期保险的期限，在k年末改为展期保险后，其未来损失为：其中k CV为常数。

对上式两边取方差，可得改为展期保险后，在时间k的未来损失方差为：所以，改为展期保险后的未来损失方差与原保险在时间k的未来损失方差之比为：3．向30岁的投保人发行的1单位保额、连续型20年期两全保险，在10年末中止，并且那时还有一笔以10CV为抵押的贷款额L尚未清偿。

用趸缴净保费表示：（1）在保额为1-L的展期保险可展延到原期满时的情况下，期满时的生存给付金额E。

（2）转为第（1）小题中展期保险与生存保险后5年时的责任准备金。

解：如果金额为b的保单在解约时还欠有额度为L的保单贷款，那么展期保险通常提供的保险金额为b-L。

若无此条款，则借款L的保单持有人就可通过解约使原本的死亡收益b-L增加到b。

在未偿还保单贷款的情形下，采用计算。

（1）由上可得，期满时的生存给付金额E为：（2）展期保险与生存保险后5年时的责任准备金为：4．考虑x岁投保的缴费期为n的n年期两全保险，保险金为1单位，支付基础为完全离散的。

在拖欠保费的情况下，被保险人可选择：（1）减额缴清终身寿险，或（2）期限不超过原两全保险的展期定期保险以及x＋n岁时支付的减额生存保险。

第16章保单现金价值及退保选择1．已知5年期两全保险，3年缴清，保险金额为1000元，G=300元，i=5%，且求各年的资产份额。

解：由公式有，将表中数据代入上式，则可得各年的资产份额分别为2．假设x岁购买的单位保额完全连续终身寿险在k年末转为不丧失现金价值，且，分别按：（1）缴清保险（2）展期保险，给出刚改变后的保险的未来损失方差与原保险在时间k的未来损失方差之比。

解：原保险在时间k的未来损失为：对上式两边取方差，可得原保险在时间k的未来损失方差为：（1）用b k表示在时刻k的缴清保险的保险金额，则，在k年末改为缴清保险后，其未来损失为：其中k CV为常数。

对上式两边取方差，可得改为缴清保险后，在时间k的未来损失方差为：所以，改为缴清保险后的未来损失方差与原保险在时间k的未来损失方差之比为：。

（2）用s表示购买展期保险的期限，在k年末改为展期保险后，其未来损失为：其中k CV为常数。

对上式两边取方差，可得改为展期保险后，在时间k的未来损失方差为：所以，改为展期保险后的未来损失方差与原保险在时间k的未来损失方差之比为：3．向30岁的投保人发行的1单位保额、连续型20年期两全保险，在10年末中止，并且那时还有一笔以10CV为抵押的贷款额L尚未清偿。

用趸缴净保费表示：（1）在保额为1-L的展期保险可展延到原期满时的情况下，期满时的生存给付金额E。

（2）转为第（1）小题中展期保险与生存保险后5年时的责任准备金。

解：如果金额为b的保单在解约时还欠有额度为L的保单贷款，那么展期保险通常提供的保险金额为b-L。

若无此条款，则借款L的保单持有人就可通过解约使原本的死亡收益b-L增加到b。

在未偿还保单贷款的情形下，采用计算。

（1）由上可得，期满时的生存给付金额E为：（2）展期保险与生存保险后5年时的责任准备金为：4．考虑x岁投保的缴费期为n的n年期两全保险，保险金为1单位，支付基础为完全离散的。

在拖欠保费的情况下，被保险人可选择：（1）减额缴清终身寿险，或（2）期限不超过原两全保险的展期定期保险以及x+n岁时支付的减额生存保险。

第2章人寿保险的精算现值选择题1．30岁的人购买保额为1000元的特殊的35年期两全保险，已知条件如下：（1）在其购买保险时，其两个孩子的年龄分别是3岁和6岁；（2）特殊约定为：如果被保险人死亡时两个孩子的年龄都小于11岁，那么给付额为3000元；如果被保险人死亡时只有一个孩子的年龄小于11岁，那么给付额为2000元；（3）在被保险人死亡时立即给付保险金；（4）μ30＋t=0.04，t≥0；（5）δ=0.06；（6）35E30=0.0302。

则此保单的趸缴纯保费为（）元。

[2008年真题]A．638B．766C．777D．796E．800【答案】D【解析】由题意可知，该保险相当于保额1000元的35年期两全保险＋1000元保额的8年期定期保险（5-8年内被保险人只有一个孩子小于11岁）＋1000元保额的5年期定期保险（5年内两个孩子都小于11岁），故此保单的趸缴保险费为：=796（元）2．30岁的人购买两年期定期保险，保险金在被保险人死亡的年末给付，保单年度t 的保额为bt ，已知条件为：q30=0.1，b2=10－b1，q31=0.6，i=0 ，Z表示给付现值随机变量，则使得Var（Z）最小的b1的值为（）。

[2008年真题]A．0.0B．5.0C．6.8D．8.6E．8.9【答案】C【解析】v=1，由题意得：Pr [K（30）=0]=q30=0.1，Pr [K（30）=1]=p30q31=（1－0.1）×0.6=0.54，所以E（Z）=b1×0.1＋（10－b1）×0.54，E（Z）2= ×0.1＋（10－b12）×0.54，故Var（Z）=E（Z2）－（E（Z））2= －6.048b1＋24.84。

故当b1=6.048/（2×0.4464）=6.8时，Var（Z）最小。

3．50岁的人购买保险金在死亡时给付的特殊的递增型终身寿险，Z表示给付现值随机变量，已知：b t=1＋0.1t，v t=（1＋0.1t）－2，t p50·μ（50＋t）=0.02 ，0≤t<50则Var（Z）的值为（）。

精算数学练习题1. 计算以下年金的现值：- 年金每年末支付1000元，连续支付10年，年利率为5%。

- 年金每年末支付1200元，连续支付15年，年利率为4%。

2. 假设一个保险公司签发一份保额为100万元的定期寿险保单，保险期限为5年，年利率为3%，求该保单的精算现值。

3. 计算以下生存年金的精算现值：- 年金每年初支付1500元，连续支付20年，生存者的年龄为30岁，年利率为6%。

- 年金每年末支付2000元，连续支付25年，生存者的年龄为45岁，年利率为5%。

4. 某保险公司提供一种终身年金，每年初支付1000元，购买者年龄为50岁，年利率为4%，求该年金的精算现值。

5. 计算以下联合生存年金的精算现值：- 年金每年末支付1500元，只要两个生存者中至少有一个存活，连续支付20年，两个生存者的年龄分别为60岁和55岁，年利率为5%。

- 年金每年初支付2000元，只要两个生存者都存活，连续支付25年，两个生存者的年龄分别为40岁和35岁，年利率为4%。

6. 假设一个保险公司签发一份保额为50万元的终身寿险保单，购买者年龄为40岁，年利率为3%，求该保单的精算现值。

7. 计算以下递增年金的精算现值：- 年金每年末支付1000元，连续支付10年，每年支付额递增5%，年利率为6%。

- 年金每年初支付1200元，连续支付15年，每年支付额递增3%，年利率为5%。

8. 某保险公司提供一种递减定期寿险，保险期限为10年，每年初支付保费1000元，购买者年龄为30岁，年利率为4%，求该保单的精算现值。

9. 计算以下年金的精算现值，其中包含一个保证期：- 年金每年末支付1000元，连续支付10年，保证期为5年，年利率为5%。

- 年金每年初支付1200元，连续支付15年，保证期为8年，年利率为4%。

10. 假设一个保险公司签发一份保额为200万元的终身寿险保单，购买者年龄为50岁，年利率为3%，求该保单的精算现值。

第12章特殊年金与保险
计算题：
1．假设每年内死亡服从均匀分布，证明式可表示为：
解：由于死亡服从均匀分布，
2．证明中定义的Z和每年支付1的n年延期连续生命年金有相同的方差。

解：每年支付1的n年延期连续生命年金的随机变量可表示为：
3．对部分现金立即偿还年金.设现值随机变量为：
证明对部分现金立即偿还年金，式可写成：
解：直接求期望可得：
4．证明：有：
解：因为
5．假设
证明：
解：
因为Z2是常量，Z1为n年定期死亡保险的现值随机变量，故
6．一份保单从（x）死亡日期开始提供每年为1的连续确定年金。

如死亡发生在保单签发后的15年内，则年金支付到保单签发后的20年年底；如死亡发生在保单签发后15至20年内，则年金支付5年。

保单签发20年后终止。

给出趸缴净保费的表达式。

解：设保单给付现值的随机变量为Z，可得：
7．某份保单规定：如被保险人在20年末还活着时可得1000元；如在保单签发后的20年内死亡，则每月可得10元的收入直至20年末，该收入的第一笔支付在死亡的月末，保单签发20年后则无支付。

给出x岁时的年缴净保费公式。

解：
8．证明：
解：
9．证明：对一个退休收入保单，记a=h＋r，其中h=[a]，0＜r＜1，则在第h＋1保单年度内死亡均匀分布的假设下下式成立：
解：
10．证明：
解：。