利用旋转液体测重力加速度

旋转液体测重力加速度的研究摘要：本文对旋转液体测重力加速度的研究进行了介绍和探讨。

首先，介绍了测量重力加速度的一般方法和技术，然后阐述了旋转液体测重力加速度的原理和优点，包括可以测量超高精度、可以同时测量多个测量点、可以实现非常迅速的测量等等。

接着，提出了通过改进实验装置和算法等方式来提高旋转液体测重力加速度测量精度的建议。

最后，分析了旋转液体测重力加速度的发展前景和应用前景。

关键词：旋转液体测重力加速度；重力加速度；精度；测量点；测量速度引言：重力加速度是物理学中一个非常重要的概念，它可以用来描述物体在重力作用下的加速度，也是很多物理学和天文学问题的基础。

因此，测量重力加速度一直是物理学研究的一个重要课题。

目前，测量重力加速度的方法和技术已经非常成熟，包括重力仪、挂钩式重力仪、细丝重力仪等等。

在这些测量方法中，重力仪是应用最广泛的一种，它使用弹簧系统来测量物体在重力作用下的加速度。

然而，传统的重力仪存在一些缺点，比如精度有限、只能同时测量一个测量点等等。

因此，在最近几十年来，研究人员开始探索一些新的方法和技术来测量重力加速度。

其中，旋转液体测重力加速度是一种新兴的测量方法，它通过对液体的旋转状态进行测量来推算重力加速度，具有高精度、高速度和同时测量多个测量点等优点。

本文将对旋转液体测重力加速度的原理、优点和发展前景进行探讨，并提出一些改进实验装置和算法等方式来提高其测量精度。

旋转液体测重力加速度是利用摩擦力产生的离心力对液体进行旋转来测量重力加速度的一种新兴方法。

它的基本原理是利用离心力对液体进行旋转，并测量液体旋转状态的变化来固定重力加速度。

具体来说，液体在旋转时，由于离心力的作用，液体的形状、密度和旋转速度都会发生变化。

通过测量液体旋转状态的变化，就可以计算出重力加速度的大小和方向。

为了实现高精度的测量，旋转液体测重力加速度通常需要利用高速摄像机、激光干涉仪等先进的测试设备来进行测量。

与传统的重力仪相比，旋转液体测重力加速度具有多个优点，包括：1.高精度：旋转液体测重力加速度可以达到非常高的精度，比如在10^-9 g的级别之内。

一、实验目的1. 了解旋转液体在旋转过程中产生的物理现象；2. 掌握测量旋转液体表面形状、离心力、重力加速度等参数的方法；3. 分析旋转液体在不同转速下的物理特性。

二、实验原理旋转液体实验是基于牛顿第二定律和牛顿万有引力定律。

当液体在旋转容器中旋转时，液体受到离心力和重力的作用，形成特殊的物理现象。

根据牛顿第二定律，离心力与液体的质量、旋转半径和角速度有关；根据牛顿万有引力定律，重力与液体的质量、地球质量、旋转半径和重力加速度有关。

三、实验仪器与设备1. 旋转液体实验装置：包括旋转容器、旋转电机、测速仪、激光测距仪等；2. 数据采集系统：包括计算机、数据采集卡、软件等；3. 其他：秒表、天平、刻度尺等。

四、实验步骤1. 将旋转液体实验装置安装好，确保旋转容器、旋转电机、测速仪、激光测距仪等设备正常运行；2. 在旋转容器中倒入适量的液体，调整液面高度，确保液体表面平坦；3. 打开旋转电机，缓慢增加转速，观察液体表面形状、涡流等现象；4. 利用激光测距仪测量液体表面形状，记录数据；5. 利用测速仪测量旋转液体的角速度；6. 利用天平测量液体的质量；7. 记录实验数据，包括转速、角速度、液体表面形状、离心力、重力加速度等。

五、实验数据1. 实验过程中，液体表面形状呈现抛物线状，随着转速的增加，抛物线越来越陡峭；2. 实验测得旋转液体的角速度与转速成正比；3. 实验测得离心力与液体质量、旋转半径和角速度的平方成正比；4. 实验测得重力加速度与液体质量、地球质量、旋转半径的平方成反比。

六、实验结果与分析1. 旋转液体表面形状：实验结果显示，随着转速的增加，液体表面形状逐渐变为抛物线状，符合牛顿第二定律；2. 离心力：实验结果显示，离心力与液体质量、旋转半径和角速度的平方成正比，符合牛顿第二定律；3. 重力加速度：实验结果显示，重力加速度与液体质量、地球质量、旋转半径的平方成反比，符合牛顿万有引力定律。

七、实验结论1. 旋转液体实验验证了牛顿第二定律和牛顿万有引力定律的正确性；2. 通过旋转液体实验，可以测量液体表面形状、离心力、重力加速度等参数；3. 旋转液体实验为研究旋转液体在旋转过程中的物理现象提供了实验依据。

大学物理实验预习报告两汉：诸葛亮先帝创业未半而中道崩殂，今天下三分，益州疲弊，此诚危急存亡之秋也。

然侍卫之臣不懈于内，忠志之士忘身于外者，盖追先帝之殊遇，欲报之于陛下也。

诚宜开张圣听，以光先帝遗德，恢弘志士之气，不宜妄自菲薄，引喻失义，以塞忠谏之路也。

宫中府中，俱为一体；陟罚臧否，不宜异同。

若有作奸犯科及为忠善者，宜付有司论其刑赏，以昭陛下平明之理；不宜偏私，使内外异法也。

侍中、侍郎郭攸之、费祎、董允等，此皆良实，志虑忠纯，是以先帝简拔以遗陛下：愚以为宫中之事，事无大小，悉以咨之，然后施行，必能裨补阙漏，有所广益。

将军向宠，性行淑均，晓畅军事，试用于昔日，先帝称之曰“能”，是以众议举宠为督：愚以为营中之事，悉以咨之，必能使行阵和睦，优劣得所。

亲贤臣，远小人，此先汉所以兴隆也；亲小人，远贤臣，此后汉所以倾颓也。

先帝在时，每与臣论此事，未尝不叹息痛恨于桓、灵也。

侍中、尚书、长史、参军，此悉贞良死节之臣，愿陛下亲之、信之，则汉室之隆，可计日而待也。

臣本布衣，躬耕于南阳，苟全性命于乱世，不求闻达于诸侯。

先帝不以臣卑鄙，猥自枉屈，三顾臣于草庐之中，咨臣以当世之事，由是感激，遂许先帝以驱驰。

后值倾覆，受任于败军之际，奉命于危难之间，尔来二十有一年矣。

先帝知臣谨慎，故临崩寄臣以大事也。

受命以来，夙夜忧叹，恐托付不效，以伤先帝之明；故五月渡泸，深入不毛。

今南方已定，兵甲已足，当奖率三军，北定中原，庶竭驽钝，攘除奸凶，兴复汉室，还于旧都。

此臣所以报先帝而忠陛下之职分也。

至于斟酌损益，进尽忠言，则攸之、祎、允之任也。

愿陛下托臣以讨贼兴复之效，不效，则治臣之罪，以告先帝之灵。

若无兴德之言，则责攸之、祎、允等之慢，以彰其咎；陛下亦宜自谋，以咨诹善道，察纳雅言，深追先帝遗诏。

臣不胜受恩感激。

今当远离，临表涕零，不知所言。

竭诚为您提供优质文档/双击可除旋转液体综合实验实验报告篇一：旋转液体综合实验旋转液体综合实验浙江大学物理实验教学中心20XX-11旋转液体综合实验在力学创建之初，牛顿的水桶实验就发现，当水桶中的水旋转时，水会沿着桶壁上升。

旋转的液体其表面形状为一个抛物面，可利用这点测量重力加速度；旋转液体的抛物面也是一个很好的光学元件。

美国的物理学家乌德创造了液体镜面，他在一个大容器里旋转水银，得到一个理想的抛物面，由于水银能很好地反射光线，所以能起反射镜的作用。

随着现代技术的发展液体镜头正在向一“大”一“小”两极发展。

大，可以作为大型天文望远镜的镜头；反射式液体镜头已经在大型望远镜中得到了应用，代替传统望远镜中使用的玻璃反射境。

当盛满液体（通常采用水银）的容器旋转时，向心力会产生一个光滑的用于望远镜的反射凹面。

通常这样一个光滑的曲面，完全可以代替需要大量复杂工艺并且价格昂贵的玻璃镜头，而哈勃空间望远镜的失败也让我们了解了玻璃镜头何等脆弱。

小，则可以作为拍照手机的变焦镜头。

美国加利福尼亚大学的科学家发明了液体镜头，它通过改变厚度仅为8mm的两种不同的液体交接处月牙形表面的形状，实现焦距的变化。

这种液体镜头相对于传统的变焦系统而言，兼顾了紧凑的结构和低成本两方面的优势。

旋转液体的综合实验可利用抛物面的参数与重力加速度关系，测量重力加速度，另外，液面凹面镜成像与转速的关系也可研究凹面镜焦距的变化情况。

还可通过旋转液体研究牛顿流体力学，分析流层之间的运动，测量液体的粘滞系数。

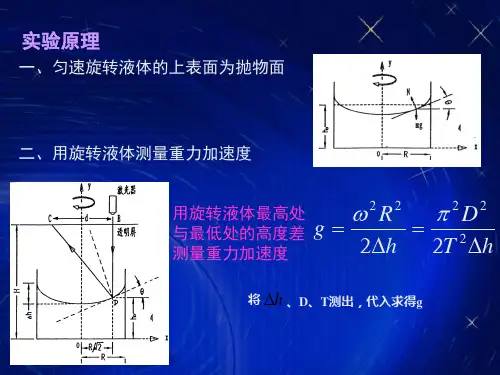
【实验原理】一、旋转液体抛物面公式推导定量计算时，选取随圆柱形容器旋转的参考系，这是一个转动的非惯性参考系。

液相对于参考系静止，任选一小块液体p，其受力如图1。

Fi为沿径向向外的惯性离心力，mg为重力，n为这一小块液体周围液体对它的作用力的合力，由对称性可知，n必然垂直于液体表面。

在x-Y坐标下p(x,y)则有：图1原理图ncos??mg?0nsin??Fi?0Fi?m?x2tan??dydx??xg2根据图1有：y??22x?y0（1）2g为旋转角速度，y0为x?0处的y值。

旋转液体综合实验浙江大学物理实验教学中心2005-11旋转液体综合实验在力学创建之初，牛顿的水桶实验就发现，当水桶中的水旋转时，水会沿着桶壁上升。

旋转的液体其表面形状为一个抛物面，可利用这点测量重力加速度；旋转液体的抛物面也是一个很好的光学元件。

美国的物理学家乌德创造了液体镜面，他在一个大容器里旋转水银，得到一个理想的抛物面，由于水银能很好地反射光线，所以能起反射镜的作用。

随着现代技术的发展液体镜头正在向一“大”一“小”两极发展。

大，可以作为大型天文望远镜的镜头； 反射式液体镜头已经在大型望远镜中得到了应用，代替传统望远镜中使用的玻璃反射境。

当盛满液体（通常采用水银）的容器旋转时，向心力会产生一个光滑的用于望远镜的反射凹面。

通常这样一个光滑的曲面，完全可以代替需要大量复杂工艺并且价格昂贵的玻璃镜头，而哈勃空间望远镜的失败也让我们了解了玻璃镜头何等脆弱。

小，则可以作为拍照手机的变焦镜头。

美国加利福尼亚大学的科学家发明了液体镜头，它通过改变厚度仅为8mm 的两种不同的液体交接处月牙形表面的形状，实现焦距的变化。

这种液体镜头相对于传统的变焦系统而言，兼顾了紧凑的结构和低成本两方面的优势。

旋转液体的综合实验可利用抛物面的参数与重力加速度关系，测量重力加速度，另外，液面凹面镜成像与转速的关系也可研究凹面镜焦距的变化情况。

还可通过旋转液体研究牛顿流体力学，分析流层之间的运动，测量液体的粘滞系数。

【实验原理】一、 旋转液体抛物面公式推导定量计算时，选取随圆柱形容器旋转的参考系，这是一个转动的非惯性参考系。

液相对于参考系静止，任选一小块液体P ，其受力如图1。

Fi 为沿径向向外的惯性离心力，mg 为重力，N 为这一小块液体周围液体对它的作用力的合力，由对称性可知，N 必然垂直于液体表面。

在X-Y 坐标下P(x,y) 则有：cos 0N mg θ-= sin 0i N F θ-=图1 原理图2i F m x ω=2tan dy xdx gωθ==根据图1有： 0222y x gy +=ω （1）为旋转角速度，0y 为0=x 处的y 值。

旋转液体综合实验浙江大学物理实验教学中心2005-11旋转液体综合实验在力学创建之初，牛顿的水桶实验就发现，当水桶中的水旋转时，水会沿着桶壁上升。

旋转的液体其表面形状为一个抛物面，可利用这点测量重力加速度；旋转液体的抛物面也是一个很好的光学元件。

美国的物理学家乌德创造了液体镜面，他在一个大容器里旋转水银，得到一个理想的抛物面，由于水银能很好地反射光线，所以能起反射镜的作用。

随着现代技术的发展液体镜头正在向一“大”一“小”两极发展。

大，可以作为大型天文望远镜的镜头；反射式液体镜头已经在大型望远镜中得到了应用，代替传统望远镜中使用的玻璃反射境。

当盛满液体（通常采用水银）的容器旋转时，向心力会产生一个光滑的用于望远镜的反射凹面。

通常这样一个光滑的曲面，完全可以代替需要大量复杂工艺并且价格昂贵的玻璃镜头，而哈勃空间望远镜的失败也让我们了解了玻璃镜头何等脆弱。

小，则可以作为拍照手机的变焦镜头。

美国加利福尼亚大学的科学家发明了液体镜头，它通过改变厚度仅为8mm的两种不同的液体交接处月牙形表面的形状，实现焦距的变化。

这种液体镜头相对于传统的变焦系统而言，兼顾了紧凑的结构和低成本两方面的优势。

旋转液体的综合实验可利用抛物面的参数与重力加速度关系，测量重力加速度，另外，液面凹面镜成像与转速的关系也可研究凹面镜焦距的变化情况。

还可通过旋转液体研究牛顿流体力学，分析流层之间的运动，测量液体的粘滞系数。

【实验原理】一、旋转液体抛物面公式推导定量计算时，选取随圆柱形容器旋转的参考系，这是一个转动的非惯性参考系。

液相对于参考系静止，任选一小块液体P，其受力如图1。

Fi为沿径向向外的惯性离心力，mg为重力，N为这一小块液体周围液体对它的作用力的合力，由对称性可知，N必然垂直于液体表面。

在X-Y坐标下P(x,y)则有：图1 原理图cos 0N mg θ-= sin 0i N F θ-=2i F m x ω=2tan dy xdx gωθ==根据图1有： 0222y x gy +=ω （1）为旋转角速度，0y 为0=x 处的y 值。

一、实验目的1. 了解水中旋转液体所表现出的物理现象。

2. 掌握利用旋转液体测量重力加速度的方法。

3. 研究旋转液体表面形状与重力加速度、旋转角速度之间的关系。

4. 探讨旋转液体在光学系统中的应用。

二、实验原理当圆柱形容器中的液体绕其圆柱面的对称轴匀速转动时，液体表面会形成一个抛物面。

这是由于液体在旋转过程中受到惯性离心力的作用，使得液体表面呈现出向外的倾斜。

根据旋转液体表面形状与重力加速度、旋转角速度之间的关系，可以推导出旋转液体表面方程：\[ y = \frac{1}{2} a r^2 \]其中，\( y \) 为液体表面高度，\( a \) 为重力加速度，\( r \) 为液体表面半径。

通过测量旋转液体表面形状的参数，可以计算出重力加速度。

此外，旋转液体的抛物面还可以作为光学元件，用于光学系统的研究。

三、实验仪器与材料1. 圆柱形容器2. 水银3. 旋转装置4. 游标卡尺5. 水平仪6. 激光测距仪7. 摄像机四、实验步骤1. 将圆柱形容器充满水银，确保液体表面平整。

2. 将旋转装置安装在圆柱形容器上，调整水平仪，确保旋转装置水平。

3. 启动旋转装置，使水银绕圆柱面的对称轴匀速转动。

4. 利用游标卡尺测量液体表面形状的参数，包括液体表面半径、表面高度等。

5. 利用激光测距仪测量液体表面形状的参数，包括液体表面半径、表面高度等。

6. 将测量数据输入计算机，进行数据处理和分析。

7. 计算重力加速度，并与理论值进行比较。

五、实验结果与分析1. 通过实验，观察到水中旋转液体表面呈现出抛物面形状，证实了旋转液体表面方程的正确性。

2. 利用实验数据计算出的重力加速度与理论值基本吻合，误差在可接受范围内。

3. 通过分析旋转液体表面形状与重力加速度、旋转角速度之间的关系，进一步了解了旋转液体的物理特性。

六、实验结论1. 旋转液体表面呈现出抛物面形状，是由于液体在旋转过程中受到惯性离心力的作用。

2. 通过测量旋转液体表面形状的参数，可以计算出重力加速度。

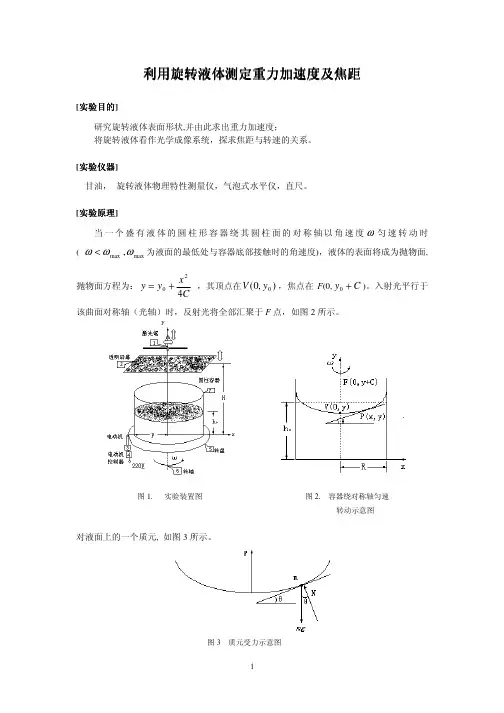
利用旋转液体测定重力加速度利用旋转液体测定重力加速度及焦距[实验目的]研究旋转液体表面形状,并由此求出重力加速度；将旋转液体看作光学成像系统，探求焦距与转速的关系。

[实验仪器]甘油，旋转液体物理特性测量仪，气泡式水平仪，直尺。

[实验原理]当一个盛有液体的圆柱形容器绕其圆柱面的对称轴以角速度ω匀速转动时( max max ,ωωω<为液面的最低处与容器底部接触时的角速度)，液体的表面将成为抛物面, 抛物面方程为：C x y y 42 0+= ，其顶点在),0(0y V ，焦点在F (0,C y +0)。

入射光平行于该曲面对称轴（光轴）时，反射光将全部汇聚于F 点，如图2所示。

图1. 实验装置图图2. 容器绕对称轴匀速转动示意图对液面上的一个质元, 如图3所示。

图3 质元受力示意图当其处于平衡时有:mg N x m N ==θωθcos sin 2故液面的形状可表示为g x dx dy 2tan ωθ== 因而0222y g x y +=ω式中y 0是在x=0时的高度.设抛物面上一点（x 0,h 0） g x y h 220200ω+=20020)(2ωy h g x -=(1) 由于液体的体积不变，则()xdx g x y xdx y h R R R+==0022002222ωπππ y 0=g R h 4220ω-(2) 由方程（1），（2）可得20Rx = (3)由（3）式可知液面在x 0处的高度是恒定的。

将激光垂直照射x=x 0处液面，在屏上读出反射光点与入射光点的距离x '。

入射角为θ ，反射角为θ，入射光线与反射光线的夹角为2θ，则 ()0)2tan(h H x -'=θ 。

[实验内容]1．利用气泡式水平仪将屏幕、转盘调至水平位置。

2．测出)2(,,0R D H h =3．逐渐改变转动角速度，待液体处于平衡态时，将激光垂直照射x=x 0处液面，在屏上读出反射光点与入射光点的距离x '。

旋转液体测重力加速度的研究摘要：本文通过对旋转液体反射的原理以及斜率法的综合运用，从而对重力加速度g进行了测量。

研究旋转液体浓度与重力加速度之间的存在的关系，利用origin软件找出不同浓度液体测g值得拟合，并对旋转液体反射方法所得g值与当地g值比较，给出最好的重力加速度测量方法，得出最准确的液体浓度。

关键词：旋转液体；重力加速度；浓度；抛物面方程1 引言:重力加速度通常用g 表示，一般取9.802/m s。

它是一个非常重要的地球物理常数，其值随着地理纬度和海拔高度的不同而不同。

准确测定不同地区的重力加速度在理论上、生产上以及科学研究中都具有重要的意义。

对重力加速度的多种不同测量方法及它们各自的设计思想和实验技巧等进行分析研究，将会加深我们对物理实验的基本思想、方法和技能的掌握，培养实验设计能力和创造性思维。

所以重力加速度在大学物理实验中是重要的一个基本物理实验。

根据盐城所在的纬度为北纬33022’，经度为东经120012’，我们能够得出盐城本地重力加速度为9.7982m s./光是一种人类眼睛可以见到的电磁波。

在科学的定义上，光有时候是指所有的电磁波谱。

光是由一种称为光子的基本粒子组成。

具有粒子性和波动性，或称为波粒二象性。

光遇到水面、玻璃等其他许多物体的表面都会发生反射，光线从一种介质斜射入另一种介质时，方向发生偏折，这种现象叫做光的折射。

本专业为光电技术，所以选用了旋转液体这一实验进行研究。

旋转的液体有许多独特的物理特征,比如盛有液体的圆柱形容器绕其圆柱面的对称轴匀速转动时,旋转液体的表面将成为抛物面.由于旋转液体的表面是一个非常理想的抛物面，同时旋转液体能很好地反射光线，故而能起反射镜的作用，从而测重力加速度。

而本文探讨的是在温度不变，液体浓度不一的情况下，因此导致液体的粘滞系数不同得出最接近于本地重力加速度的液体浓度。

FB805型旋转液体综合实验仪是此次实验电子仪器，该仪器配备了半导体激光器、霍尔传感器结合单片机测量转动周期等技术。