下载文档原格式
信号与系统复习第一章 信号与系统一、基础知识1. 在连续时间范围内（）有定义的信号称为连续时间信号，简称连续信号。
2. 仅在一些离散的瞬间才有定义的信号称为离散时间信号，简称离散信号。
3. 周期信号是定义在区间，每个一定时间T （或整数N ），按相同规律重复变化的信号。
连续周期信号为；离散周期信号为，m 为零和整数。
注意离散信号的周期性，只有当为有理数时，序列才存在周期，否则不存在周期，故为非周期序列。
4. 物理可实现的信号常常为时间t （或k ）的实函数，其在各时间的函数（或序列）值为实数；复数函数（或序列）值为复数的信号称为复信号，最常用的是复指数信号。
5. 若信号的能量有界（即（能量），这时（功率）），则称其为能量有限信号，简称为能量信号；若信号的功率有界（即，这时），则称其为功率有限信号，建成为功率信号。
6. 冲激函数的取样性质定义为，。
7. 冲激函数的移位性质定义为，。
8. 冲激函数的尺度变换性质为，冲激函数为偶函数。
9. 阶跃信号可以表达函数在时间上的区域，如门函数。
10. 当系统的激励为连续信号，若其响应也是连续信号，则称其为连续系统；当系统的激励为离散信号时，若其响应也是离散信号，则称其为离散系统。
11. 系统的线性性两个含义：齐次性和可加性；线性系统的完全响应为零状态响应（或）和零输入响应（或）的和，即。
t -∞<<∞t -∞<<∞()()f t f t mT =+()()f k f k mN =+()sin()f k k α=2πα()f t 0E <<∞0P =()f t 0P <<∞0E =()()(0)f t t dt f δ∞-∞=⎰()()(0)f t t dt f δ∞-∞''=-⎰00()()()f t t t dt f t δ∞-∞-=⎰11()()()f t t t dt f t δ∞-∞''-=-⎰1()()||at t a δδ=()()()g t t t τετετ=+--()zs y ()f y ()zi y ()x y ()()()zi zs y y y =+12. 由于时不变系统的参数不随时间变化，故系统的零状态响应形式就与输入信号接入时间无关。
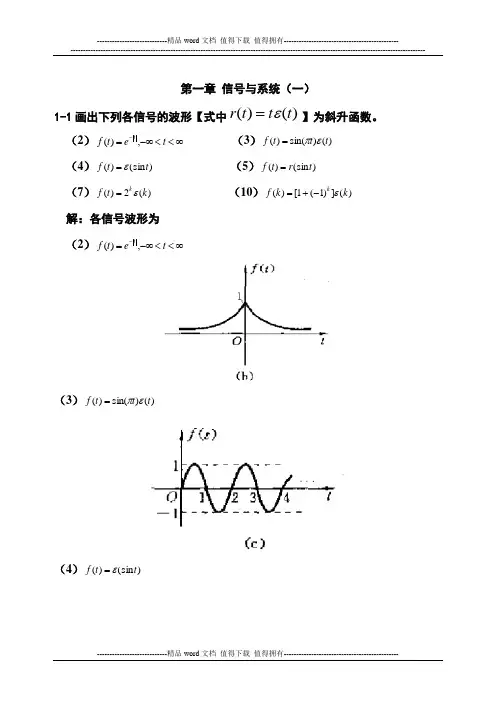
第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t（7）)t=(kf kε(2)（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。
信号与系统(吴大正)--完整版答案--纠错修改后版本2345（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为6（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε7（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε81-3 写出图1-3所示各波形的表达式。
91-4 写出图1-4所示各序列的闭合形式表达式。
101-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
（2）)63cos()443cos()(2ππππ+++=k k k f（5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。
（1）)()1(t t f ε- （2）)1()1(--t t f ε （5）)21(t f - （6）)25.0(-t f（7）dtt df )( （8）dx x f t ⎰∞-)(解：各信号波形为（1）)()1(t t f ε-（2）)1()1(--t t fε（5）)21(t f- （6）)25.0(-tf（7）dtt df )(（8）dxx f t⎰∞-)(1-7 已知序列)(k f 的图形如图1-7所示，画出下列各序列的图形。
第一章 信号与系统信号的分类确定信号 周期信号 连续时间信号 能量信号 信号信号信号信号信号的时域运算（1）移位()为常数00,t t t f +00>t ，()0t t f +为()t f 波形在t 轴上左移0t ； 00<t ，()0t t f +为()t f 波形在t 轴上右移0t .（2）反转()t f -()t f -波形为()t f 波形以0=t 为轴反转。
（3）尺度变换()at f ，a 为常数1>a ，()at f 波形为()t f 的波形在时间轴上 为原来的a 1；10<<a ，()at f 波形为()t f 的波形在时间轴上 为原来的a1；（4）微分运算 )(t f dtd（5）积分运算 ττd f t⎰∞-)(（6）相加 )()()(21t f t f t f += （7）相乘)()()(21t f t f t f ∙=奇异信号（1）阶跃函数，=)(t ε ，，（2）冲激函数0,≠tDirac 定义（3）阶跃函数与冲激函数的关系=)(t δ =)(t ε（4）阶跃函数的积分)(t r斜坡函数===)()(t t t r ε,0,0><t t t（5）冲激函数的导数和积分)(t δ'称为='=⎰⎰∞∞-∞∞-dt t dt t )()(δδ（6）冲激函数的性质 1.相乘性质)()(0t t t f -δ=-=-')()(0t t t f δ2.抽样性质=-⎰∞∞-dt t t t f )()(0δ =-'⎰∞∞-dt t t t f )()(0δ3、尺度变换性=)(at δ=)()(at n δ4.偶对称性=)(t δ第二章 连续系统的时域分析2.1 L TI 连续系统的响应n 阶常系数线性微分方程的全解由齐次解和特解组成，即+=)(t y齐次解（二阶0=+'+''qy y p y ）1）21λλ≠时，+=y2）21λλ=时，=y3）i βαλ+=21、时，=y特解（二阶)(x f qy y p y =+'+''）（1）kx n e x P x f )()(=① ：若k 非特征值，令=0y 如x e b ax y )(0+=② ：若k 与一个特征值相同，令kx n n e x a x a x a a y )(22100+++=如x e b ax x y )(0+=③ ：若k 与两个特征值都相同，令kx n n e x a x a x a a y )(22100+++=如x e b ax x y )(20+=（2）]sin )(cos )([)(x x P x x P e x f s l x ββα+=令},max{s l n =① ：若βαi +不是特征值，令=)(0x y② ：若βαi +是特征值，令]sin )(cos )([)()2()1(0x x Q x x Q e x y n n x ββα+=如]sin )(cos )[()(0x d cx x b ax xe x y xββ+++=2.3 卷积积分一般而言，两个函数)()(21t f t f 和卷积=*=)()()(21t f t f t fLTI 系统的零状态响应)(t y zs 是激励)(t f 与冲激响应)(t h 的卷积积分。
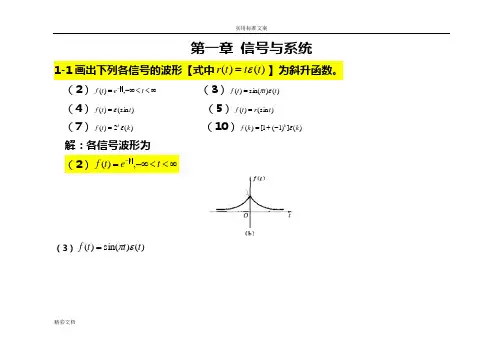
精彩文档第一章 信号与系统1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为（2）∞<<-∞=-t e t f t,)(（3）)()sin()(t t t f επ=精彩文档（4）)(sin )(t t f ε=（5）)(sin )(t r t f =（7）)(2)(k t f k ε=精彩文档（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为精彩文档（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε精彩文档（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
精彩文档1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统复习提纲第一章 信号与系统1．信号、系统的基本概念2．信号的分类，表示方法（表达式或波形）连续与离散；周期与非周期；实与复信号；能量信号与功率信号 3．信号的基本运算：加、乘、反转和平移、尺度变换。
图解时应注意仅对变量t 作变换，且结果可由值域的非零区间验证。
4．阶跃函数和冲激函数极限形式的定义；关系；冲激的Dirac 定义 阶跃函数和冲激函数的微积分关系 冲激函数的取样性质（注意积分区间）)()0()()(t f t t f δδ⋅=⋅；⎰∞∞-=⋅)0()()(f dt t t f δ)()()()(111t t t f t t t f -⋅=-⋅δδ；⎰∞∞-=-⋅)()()(11t f dt t t t f δ5．系统的描述方法数学模型的建立：微分或差分方程系统的时域框图，基本单元：乘法器，加法器，积分器（连），延时单元（离） 由时域框图列方程的步骤。
6．系统的性质线性：齐次性和可加性；分解特性、零状态线性、零输入线性。
时不变性：常参量LTI 系统的数学模型：线性常系数微分（差分）方程（以后都针对LTI 系统） LTI 系统零状态响应的微积分特性因果性、稳定性（可结合第7章极点分布判定）1． 微分方程的经典解法：齐次解+特解（代入初始条件求系数） 自由响应、强迫响应、瞬态响应、稳态响应的概念0—～0+初值（由初始状态求初始条件）：目的，方法（冲激函数系数平衡法）全响应=零输入响应+零状态响应；注意应用LTI 系统零状态响应的微积分特性 特别说明：特解由激励在t>0时或t>=0+的形式确定2． 冲激响应)(t h定义，求解（经典法），注意应用LTI 系统零状态响应的微积分特性阶跃响应)(t g 与)(t h 的关系3． 卷积积分定义及物理意义激励)(t f 、零状态响应)(t y f 、冲激响应)(t h 之间关系)()()(t h t f t y f *= 卷积的图示解法（了解）函数与冲激函数的卷积（与乘积不同）)()()(t f t t f =*δ；)()()(11t t f t t t f -=-*δ 卷积的微分与积分复合系统冲激响应的求解（了解）1．离散系统的响应差分方程的迭代法求解差分方程的经典法求解：齐次解+特解（代入初始条件求系数）全响应=零输入响应+ 零状态响应初始状态（是)()2(),1(N y y y ---Λ），而初始条件（指的是)1()1(),0(-N y y y Λ） 2．单位序列响应)(k h)(k δ的定义，)(k h 的定义，求解（经典法）； 若方程右侧是激励及其移位序列时，注意应用线性时不变性质求解 阶跃响应)(k g 与)(k h 的关系 3． 卷积和定义及物理意义激励)(k f 、零状态响应)(k y f 、冲激响应)(k h 之间关系)()()(k h k f k y f *=卷积和的作图解 )(k f 与)(k δ的卷积和)()()(k f k k f =*δ；)()()(11k k f k k k f -=-*δ结合前面卷积积分和卷积和，知道零状态响应除经典解法外的另一方法。
1．周期信号的傅立叶级数展开：两种形式三角形式：∑∑∑∞=∞=∞=+Ω+=Ω+Ω+=1110)cos(2sin cos 2)(n n n n n n n t n A A tn b t n a a t f ϕ指数形式（常用）：tjn n neF t f Ω∞-∞=∑=)(；⎰-Ω-=22)(1TT t jn n dt e t f T F周期信号的频谱（幅度谱和相位谱）：双边谱，单边谱； 频谱特点 ：离散谱线。
谱线间隔Tπ2=Ω。
信号带宽的概念2．傅立叶变换（对非周期信号和周期信号） 定义：⎰∞∞--=dt e t f j F t j ωω)()(；ωωπωd e j F t f t j ⎰∞∞-=)(21)()(ωj F 称为频谱密度函数，物理意义。
频谱：幅度谱ωω~)(j F ；相位谱ωωϕ~)(周期信号的傅立叶变换与傅立叶级数之间关系∑∞-∞=Ω-=n nT n F t f FT )(2)]([ωδπ傅立叶系数n F 的另一求法：Ω==n n j F TF ωω)(10 3．常用的FT 对 4．FT 的性质线性、奇偶性、对称性、尺度变换、时移、频移、卷积定理（时域、频域） 时域微积分性质可以只作了解（S 域中必须掌握） 5． 系统的频率响应)()()(ωωωj F j Y j H =连续系统频响的物理意义。
频域分析法求系统响应（零状态）：非周期信号输入：FT 法；周期信号输入： 傅立叶级数法 Ω=⋅=n n n j H F Y ωω)(；也可用FT 法（了解）6． 无失真传输：时域表示和频率响应如何 7． 理想滤波器的响应及物理可实现系统的条件 8． 采样定理取样前后信号的频谱图理想取样和实际取样的相同与不同时域取样，频域周期延拓。
（离散信号的频谱是周期的） 定理内容m s ωω2≥或m s f f 2≥。
能确定采样频率。
第五章 连续系统的S 域分析1． 单边拉普拉斯变换的定义及ROC dt e t f s F st ⎰∞--=0)()(ROC ：0]Re[σσ>=sS 与w 之间的关系，单边拉氏变换的特点。
2． 拉氏变换的性质线性、尺度变换、时移、频移时域微分（1次、2次）——注意初始状态是否为0、时域积分（1次） 时域卷积定理、初值终值定理 3． 拉氏逆变换的求解（)(s F 为有理真分式）要求掌握两种方法：部分分式展开法；利用常用的LT 对及LT 的性质。
4． 常用信号的LT 对5． 利用LT 求解微分方程（零输入响应、零状态响应、全响应）微分方程利用微分性质到S 域代数方程，整理成)()()(s Y s Y s Y f x +=，然后反变换。
6．系统函数)()()(s F s Y s H f =；与)(t h 的关系3个方面的应用 ：由微分方程→系统函数→求)(t h ； 系统函数转化为微分方程 求解零状态响应)(t y f 7．s 域框图时域框图→s 域框图（零状态）→s 域代数方程→响应的象函数→响应 由以上方法可得到)(t h 或)(t y f 。
若给定初始状态，可由系统函数得齐次微分方程，进一步求得)(t y x 8． 电路的s 域模型KVL KCL R 、L 、C 模型掌握零状态条件下的电路S 域模型，求解响应9． LT 与FT 的关系（知道收敛域在什么条件下可以转换，能够理解即可）第六章 离散系统的Z 域分析1． Z 变换的定义：单边和双边2． ROC 含义：是以极点为边界的连通区域（圆内、外、环）几类序列的ROC ：有限长序列，右边序列，左边序列，双边序列3． 常用序列的ZT 对 4． ZT 的性质：线性、移位性质（单边右移）、z 域尺度、k 域卷积定理、 k 域反转、部分和、初值终值定理（因果序列） 5． 逆z 变换的求解 部分分式展开法 步骤：zz F )(→按照)(z F 极点的情况进行部分分式展开→利用常用的ZT 对求逆→组合。
6． 利用ZT 求解差分方程（零输入响应、零状态响应、全响应）差分方程利用单边ZT 的移位性质得到z 域代数方程，整理成)()()(z Y z Y z Y f x +=，然后反变换。
7．系统函数)()()(z F z Y z H f =；与)(k h 的关系3个方面的应用 ：由差分方程→系统函数→求)(k h ； 系统函数转化为差分方程 求解零状态响应)(k y f 8．z 域框图k 域框图→z 域框图（零状态）→z 域代数方程→响应的象函数→响应 由以上方法可得到)(k h 或)(k y f 。
若给定初始状态，可由系统函数得齐次差分方程，进一步求得)(k y x9． S 域与z 域的关系：s 左半平面→z 单位圆内 s 右半平面→z 单位圆外 s 虚轴→z 单位圆10. 离散系统的频率响应)(θj e H 物理意义与系统函数)(z H 的关系：单位圆上的系统函数，即θθj e z j z H e H ==)()(第七章 系统函数)(•H1． 系统函数（)(s H 或)(z H ）与系统的其他描述手段的关系 微分（差分）方程、)(t h 或)(k h 、频率响应（)(ωj H 或)(θj e H ）、框图（时域和变换域）2． 零点和极点的概念 3． )(•H 与时域响应极点位于s 左半开平面的连续系统是稳定系统 极点位于z 单位圆内的离散系统是稳定系统 4．)(•H 与频域响应连续系统：ωωj s s H j H ==)()( 离散系统：θθj e z j z H e H ==)()(能根据系统函数零极点的位置定性画出幅频和相频响应曲线。
5． 全通函数和最小相移函数 定义，零极点分布的特点 6． 系统的因果性和稳定性因果性：定义、)(t h 或)(k h 因果条件、)(s H 或)(z H 的ROC 或极点位置怎样。
稳定性：定义、)(t h 的绝对可积条件或)(k h 绝对可和条件、 )(s H 或)(z H 的ROC 应包含jw 轴或单位圆。
因果稳定性（重点）：对连续系统，)(s H 的极点应在s 左半平面 对离散系统，)(z H 的极点应在单位圆内。
7． 信号流图精品文档。
11欢迎下载 熟悉基本术语、两个性质、化简规则由信号流图得到系统函数的步骤由信号流图得到系统函数也可用梅森公式8．系统模拟连续系统：加法器、数乘器、积分器；离散系统：加法器、数乘器、延时器。
由系统函数→信号流图→系统的s 或z 域框图 3种形式的实现方案：直接型、级联型、并联型。
