分金块问题的两种算法实验报告

一、实验目的1. 理解分金块问题的背景和意义；2. 掌握分治法的基本思想及其在解决分金块问题中的应用；3. 比较不同算法在解决分金块问题时的性能；4. 提高编程能力和算法设计能力。

二、实验内容1. 问题概述分金块问题是一个经典的算法问题。

问题描述如下：老板有n个金块，希望最优秀的雇员得到其中最重要的一块，最差的雇员得到其中最轻的一块。

假设有一台比较重量轻重的天平，要求设计一个算法，在尽可能少的比较次数内，将金块分为三组，使得最优秀的雇员得到最重的金块，最差的雇员得到最轻的金块。

2. 算法分析针对分金块问题，我们可以采用以下两种算法：（1）蛮力法（非递归）蛮力法的基本思想是：遍历所有可能的分组方式，找出最优解。

具体步骤如下：① 将n个金块依次编号为1至n；② 遍历所有可能的分组方式，即从第一个金块开始，将其与其他金块进行分组，然后继续对剩余的金块进行分组，直到分组完毕；③ 对于每一种分组方式，分别找出最重的金块和最轻的金块，并比较其重量；④ 找出所有分组方式中最优的分组方式，即最重的金块和最轻的金块的重量差最小。

（2）分治法分治法的基本思想是将大问题分解为若干个小问题，递归地解决这些小问题，然后合并其结果。

具体步骤如下：① 当n=1时，直接返回该金块；② 将n个金块随机分为两组，分别编号为A和B；③ 分别对A组和B组递归调用分治法，找出每组中的最重金块和最轻金块；④ 比较A组最重金块和A组最轻金块的重量差，以及B组最重金块和B组最轻金块的重量差；⑤ 根据比较结果，确定最终的最重金块和最轻金块。

三、实验步骤1. 实验环境：Python 3.72. 实验数据：随机生成100个金块，重量在1至1000之间。

3. 实验代码（1）蛮力法实现```pythondef brute_force(n):# 初始化金块重量列表weights = [i for i in range(1, n+1)]# 遍历所有可能的分组方式for i in range(1, n//2+1):for j in range(i+1, n-i+1):for k in range(j+1, n-j+1):# 计算分组方式下的最重金块和最轻金块的重量差diff_a = max(weights[i-1:k]) - min(weights[i-1:k])diff_b = max(weights[k:n]) - min(weights[k:n])# 更新最优解if diff_a < diff_b:best_a = max(weights[i-1:k])best_b = min(weights[i-1:k]) else:best_a = max(weights[k:n]) best_b = min(weights[k:n]) return best_a, best_b# 测试n = 100print(brute_force(n))```（2）分治法实现```pythondef divide_and_conquer(weights, left, right):# 当只剩一个金块时，返回该金块if left == right:return weights[left]# 将金块分为两组mid = (left + right) // 2max_a = max(weights[left:mid])min_a = min(weights[left:mid])max_b = max(weights[mid:right+1])min_b = min(weights[mid:right+1])# 比较两组金块的重量差if max_a - min_a < max_b - min_b:return max_a, min_aelse:return max_b, min_b# 测试n = 100weights = [i for i in range(1, n+1)]print(divide_and_conquer(weights, 0, n-1))```四、实验结果与分析1. 实验结果（1）蛮力法：当n=100时，运行时间约为0.6秒；（2）分治法：当n=100时，运行时间约为0.001秒。

三、主要研究内容、方法： １、内容：生活中的黄金分割 ２、方法：
（1）去图书馆查找资料，翻阅图书或相关 的书籍； （2）上网查找相关的资料； （3）询问老师；小组成员之间相互探讨。 ３、研究涉及的知识基础、所需资源： 数学的黄金比例，斐波那契数列知识，杂志、 网上所涉及的黄金比例的内容。
４、研究思路、活动步骤及进度安排：
一天合理的生活作息也应该符合黄金分割。24小时中， 2/3时间是工作与生活，1/3时间是休息与睡眠；在动与静的关 系上，究竟是“生命在于运动”，还是“生命在于静养”？从辩 证观和大量的生活实践证明，动与静的关系同一天休息与工作的 比例一样，动四分，静六分，才是最佳的保健之道。掌握与运用 好黄金分割，可使人体节约能耗，延缓衰老，提高生命质量。
[关键词] 黄金分割
0.618
和谐美
应用

二、前言： 在我们的生活中处处有数学，而历史悠久的 可说是黄金比例了。它可追溯到古代雅典的巴特 农神庙，它之所以显得那么和谐，是因为这个建 筑符合黄金比例。在我们的生活中，摄影、医学、 生物界、建筑都有黄金分割。普通书的长宽比是 黄金分割；有些植物的花瓣及主干上枝条的生长， 也隐藏着黄金分割；一些名画、雕塑、摄影作品 的主题，大多在画面的0.168…处。艺术家们认 为弦乐器的琴马放在琴弦的0.168…处，能使琴 声更加柔和甜美。由此可见黄金比例的历史和作 用。我们以“生活中的黄金分割”为课题展开研 究，进行进一步的了解，使我们了解生活中有数 学，从而热爱数学，喜欢数学。

3、植物中的黄金数 从自然界到日常生活处处都存在斐波那契数 列，存在黄金比率。某些花的花瓣数是斐波那契 数:水仙花3瓣，金凤花5瓣，翠雀花8瓣，金盏 花13瓣，紫苑花21瓣，雏菊花34，55或89瓣， 向日葵的花盘上面有21个顺时针旋形与34个逆 时针旋形；在动物中还可以发现一些软体动物的 甲壳花纹，昆虫翅膀对的数目在一定程度上符合 这个数列。

实验报告实验名称：黄金分割法院（系）：机电学院专业班级：机械制造及其自动化姓名：学号：2013年5 月13 日实验一：黄金分割法实验日期：2013年5 月13 日一、实验目的了解MATLAB的基本运用了解MATLB在优化中的使用二、实验原理黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。

其基本原理是：依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间。

三、实验内容黄金分割法程序：function [xmin,fmin]=hjfg (f,a0,b0,epsilon)a=a0; %初始化b=b0;x1=b-0.618*(b-a);f1=f(x1);x2=a+0.618*(b-a);f2=f(x2);while abs(b-a)>=epsilon %迭代求解if f1<f2 %判断缩小方向b=x2;x2=x1;f2=f1; %缩小区间x1=b-0.618*(b-a);f1=f(x1);elsea=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);f2=f(x2);endx=0.5*(a+b);endxmin=0.5*(a+b);%输出fmin=f(xmin);end函数程序：function [zhi]= fx2(x) %2²âÊÔº¯Êýzhi=2*x^2-3*x+1;end调用执行程序：[xmin2,fmin2]=hjfg (@fx2,-1,2,0.1) %2»Æ½ð·Ö¸î¼ÆËãÃüÁî执行结果：xmin2 =0.7583fmin2 =-0.1249四、实验小结通过本实验了解了了matlab的基本操作方法，了解黄金分割法法的原理与基本运用。

第九章分治策略当我们要求解一个数据规模为n且n取值又相当大的问题时，直接求解往往是非常困难的。

如果在将这n个输入分成k个不同子集合的情况下，能得到k个不同的可分别求解的子问题，其中1<k≤n，求出了这些子问题的解之后，还可找到适当的方法把它们合并成整个问题的解，那么，具备上述特性的问题可考虑使用分治策略求解。

第1课金块问题(gold)【问题描述】一个老板有一袋金块，里面有n块金子。

每个月，老板会从袋子中拿出两个金块奖励两名表现优秀的雇员。

按规矩，最优秀的雇员将得到袋中最重的金块，排名第二的雇员将得到袋中最轻的金块。

如果老板周期性地往袋中加入新的金块，那么每个月他都要找出最重和最轻的金块。

假设有一台比较质量的仪器，我们希望用尽量少的比较次数找出最重和最轻的金块。

【输入格式】第1行只有一个整数n(2≤n≤100000)。

第2行n个长整型范围内的整数，每个整数之间用一个空格隔开，表示每块金子的质量。

【输出格式】输出两个用空格分开的整数，表示最重和最轻的金块的质量。

【输入样例】8108245391【输出样例】101分析问题明显，金块问题就是在n个元素中求最大值和最小值的问题。

最直接的方法就是逐个地进行比较查找，如下面程序所示：vara:array[1..100000]of longint;i,n,max,min:longint;beginreadln(n);for i:=1to n do read(a[i]);max:=a[1];min:=a[1];for i:=2to n dobeginif a[i]>max then max:=a[i];if a[i]<min then min:=a[i];end;writeln(max,'',min);end.这种方法需要比较2n-2次。

也可以采用另一种方法，先比较n-1次求出最重的金块，再从剩下的n-1个金块中比较n-2次得到最轻的，这样总的比较次数为2n-3次（程序如下），相差只有一次。

matlab实验黄金分割法黄金分割法（Golden Section Method）是一种用于解决最优化问题的数值计算方法。

在数学上，最优化问题可以表述为寻找某个函数的最小值或最大值。

而黄金分割法是一种无约束优化算法，常被用于一维函数的最优化问题。

在本文中，我们将介绍黄金分割法的原理，并通过Matlab实验来演示其应用。

黄金分割法的原理基于黄金分割比，即1：0.618。

黄金分割法通过将搜索区间不断缩小，直到满足指定的精度要求，最终找到函数的极值点。

下面我们将逐步介绍黄金分割法的步骤：1. 初始化：给定初始搜索区间[a, b]，以及所需的精度要求ε。

2. 计算区间长度：计算区间长度L = b - a。

3. 计算划分点：计算第一个划分点x1 = a + 0.382L，以及第二个划分点x2 = a + 0.618L。

4. 计算函数值：计算在划分点x1和x2处的函数值f(x1)和f(x2)。

5. 更新搜索区间：比较f(x1)和f(x2)的大小关系，若f(x1) < f(x2)，则新的搜索区间为[a, x2]，否则为[x1, b]。

6. 判断收敛：如果L < ε，算法收敛，停止迭代；否则，返回步骤2。

接下来，我们将通过一个实例来演示黄金分割法在Matlab中的应用。

假设我们要优化以下函数：```matlabf(x) = x^2 + 5*sin(x)```首先，我们需要在Matlab中定义这个函数。

在命令窗口中输入以下代码：```matlabf = @(x) x^2 + 5*sin(x);```接下来，我们可以采用黄金分割法来最小化这个函数。

以下是Matlab代码的大致框架：```matlaba = 0;b = 10;epsilon = 0.001;L = b - a;x1 = a + 0.382*L;x2 = a + 0.618*L;while L >= epsilonf1 = f(x1);f2 = f(x2);if f1 < f2b = x2;elsea = x1;endL = b - a;x1 = a + 0.382*L;x2 = a + 0.618*L;end```以上代码中，我们使用了一个while循环来不断更新搜索区间和划分点，直到满足指定的精度要求。

很多人认为黄金分割法是搜索速度最快的方法，从程序编写角度来说，黄金分 割法每次 只需要插入一个点，每次只需要计算一次函数值，易于理解。就对区间 缩短率来讲，黄金分 割法的缩短率是 0.618，舍弃的区间是 0.382。但是，如果 一个函数是凸函数，根据已知的函数值，可以找到它的最大值和最小值，这 些信 息有利于得到最优解的位置，进而大大缩减不确定区间。
所以 f (x) 是凸函数。这个定理表明了根据局部导数的线性近似是函数的低 估，即凸函数图形位于图形上任一 点切线的上方。
根据这个定理，所以函数的最小值一定在切线的上方。利用凸函数的一阶特征 以及已知 的最小函数值就可以确定不确定区间。函数两个端点处的切线和最小函 数值的交点，即为缩 小的不确定区间。
所属课程名称 最优化
1) B2Ak+22+1=2+15+c51mc+=m5=21c11+m++12+2+1++=212=2+1+2+1+2+2+22+32k+1+2
实验项目名称 改进的黄所存在的缺点并对它进行改进。 3：熟悉应用 Matlab 求解无约束最优化问题的编程方法.
1) B2Ak+22+12=+15+c51mc+=5m=2c111++m+12+21+++2=12=2+1+2+1+2+2+22+32k+1+2
88.8918÷.12990.÷1=4214÷3922=.0034=1÷15251371=8.535.78208÷.0232173c0*0÷1=m920.30392.2c=1÷203m=2÷1202.52=3535=42314)c*5232m40341*.31252=3.*1.153.5*03134.2*920522..104455=+21*3*50202.2.0285.4850.13*50+5c8*125*12m0.2+050.+0*014.852*0051000+0+/038.T+0÷+=55*+1011+010+91÷0145405*00010200+5+0+080+40*04+***115.103910*-%*C%6(+÷*M==5M÷5)0*3*0(31÷3110**5*+*÷414.m2371e=%7)8n08%.=s8.5=77.93cc60.mc*m4*m13,101w9.9o.k24mc-.cem5nm2csp2665m*9..03-4.50c60*5.pc3m85,9cm0.5g.i50mr0l-.p.s85p/6c50bc.0om7m.yp.cs6pc5m+;c0m..m7.ckm; 1+1k+12+1+k2234=1c+m1++4+4+2

机械优化设计黄金分割法实验报告
1、黄金分割法基本思路： 黄金分割法适用于[a，b]区间上的任何单股函数求极小值问题，对 函数除要求“单谷”外不做其他要求，甚至可以不连续。因此，这 种方法的适应面非常广。黄金分割法也是建立在区间消去法原理基 础上的试探方法，即在搜索区间[a，b]内适当插入两点 a1，a2，并 计算其函数值。a1，a2 将区间分成三段，应用函数的单谷性质，通 过函数值大小的比较，删去其中一段，是搜索区间得以缩小。然后 再在保留下来的区间上作同样的处理，如此迭代下去，是搜索区间 无限缩小，从而得到极小点的数值近似解。 2 黄金分割法的基本原理 一维搜索是解函数极小值的方法之一，其解法思想为沿某一已知方 向求目标函数的极小值点。一维搜索的解法很多，这里主要采用黄 金分割法（0.618 法）。该方法用不变的区间缩短率 0.618 代替斐 波那契法每次不同的缩短率，从而可以看成是斐波那契法的近似， 实现起来比较容易，也易于人们所接受。
3 程序流程如下：
2
பைடு நூலகம்
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，通力根1保过据护管生高线产中敷工资设艺料技高试术中卷0资不配料仅置试可技卷以术要解是求决指，吊机对顶组电层在气配进设置行备不继进规电行范保空高护载中高与资中带料资负试料荷卷试下问卷高题总中2体2资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况1卷中下安，与全要过，加度并强工且看作尽护下可1都关能可于地以管缩正路小常高故工中障作资高；料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高，核中或对资者定料对值试某，卷些审弯异核扁常与度高校固中对定资图盒料纸位试，置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置，线高尤弯中其曲资要半料避径试免标卷错高调误等试高，方中要案资求，料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高，技料课中并3术试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术，、以术来管及避架系免等统不多启必项动要方高式案中，；资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资，中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置，作调合并试理且技利进术用行，管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵：导活在。。分对对线于于盒调差处试动，过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调，问试应题技采，术用作是金为指属调发隔试电板人机进员一行，变隔需压开要器处在组理事在；前发同掌生一握内线图部槽 纸故内资障，料时强、，电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料，试试线卷卷缆试切敷验除设报从完告而毕与采，相用要关高进技中行术资检资料查料试和，卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

算法实验报告一分治法实验金块问题问题描述：有一个老板有一袋金块。

每个月将有两名雇员会因其优异的表现分别被奖励一个金块。

按规矩，排名第一的雇员将得到袋中最重的金块，排名第二的雇员将得到袋中最轻的金块。

根据这种方式，除非有新的金块加入袋中，否则第一名雇员所得到的金块总是比第二名雇员所得到的金块重。

如果有新的金块周期性的加入袋中，则每个月都必须找出最轻和最重的金块。

假设有一台比较重量的仪器，我们希望用最少的比较次数找出最轻和最重的金块算法思想：分而治之方法与软件设计的模块化方法非常相似。

为了解决一个大的问题，可以：1) 把它分成两个或多个更小的问题；2) 分别解决每个小问题；3) 把各小问题的解答组合起来，即可得到原问题的解答。

小问题通常与原问题相似，可以递归地使用分而治之策略来解决。

问题分析:一般思路：假设袋中有n 个金块。

可以用函数M a x（程序1 - 3 1）通过n-1次比较找到最重的金块。

找到最重的金块后，可以从余下的n-1个金块中用类似的方法通过n-2次比较找出最轻的金块。

这样，比较的总次数为2n-3。

分治法：当n很小时，比如说，n≤2，识别出最重和最轻的金块，一次比较就足够了。

当n 较大时（n＞2），第一步，把这袋金块平分成两个小袋A和B。

第二步，分别找出在A和B中最重和最轻的金块。

设A中最重和最轻的金块分别为HA 与LA，以此类推，B中最重和最轻的金块分别为HB 和LB。

第三步，通过比较HA 和HB，可以找到所有金块中最重的；通过比较LA 和LB，可以找到所有金块中最轻的。

在第二步中，若n＞2，则递归地应用分而治之方法程序设计据上述步骤，可以得出程序1 4 - 1的非递归代码。

该程序用于寻找到数组w [ 0 : n - 1 ]中的最小数和最大数，若n < 1，则程序返回f a l s e，否则返回t r u e。

当n≥1时，程序1 4 - 1给M i n和M a x置初值以使w [ M i n ]是最小的重量，w [ M a x ]为最大的重量。

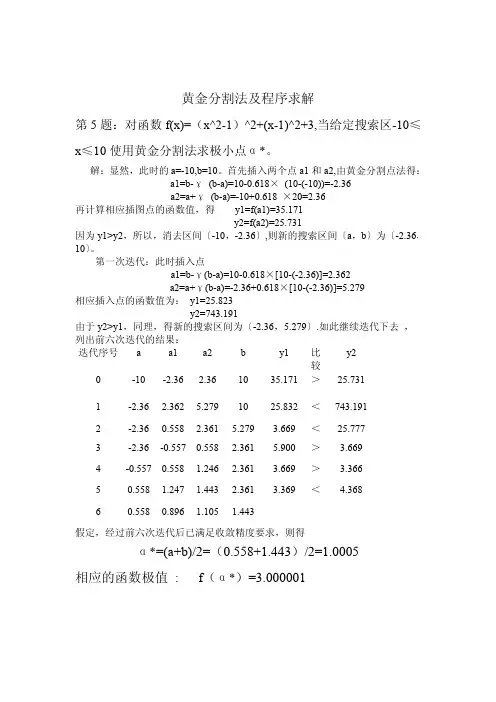
黄金分割法及程序求解第5题：对函数f(x)=（x^2-1）^2+(x-1)^2+3,当给定搜索区-10≤x≤10使用黄金分割法求极小点α*。

解：显然，此时的a=-10,b=10。

首先插入两个点a1和a2,由黄金分割点法得：a1=b-γ(b-a)=10-0.618×(10-(-10))=-2.36a2=a+γ(b-a)=-10+0.618×20=2.36再计算相应插图点的函数值，得y1=f(a1)=35.171y2=f(a2)=25.731因为y1>y2，所以，消去区间〔-10，-2.36〕,则新的搜索区间〔a，b〕为〔-2.36，10〕。

第一次迭代：此时插入点a1=b-γ(b-a)=10-0.618×[10-(-2.36)]=2.362a2=a+γ(b-a)=-2.36+0.618×[10-(-2.36)]=5.279相应插入点的函数值为：y1=25.823y2=743.191由于y2>y1，同理，得新的搜索区间为〔-2.36，5.279〕.如此继续迭代下去，列出前六次迭代的结果：y2迭代序号a a1a2b y1比较0-10-2.36 2.361035.171＞25.7311-2.36 2.362 5.2791025.832＜743.1912-2.360.558 2.361 5.279 3.669＜25.7773-2.36-0.5570.558 2.361 5.900＞ 3.6694-0.5570.558 1.246 2.361 3.669＞ 3.36650.558 1.247 1.443 2.361 3.369＜ 4.36860.5580.896 1.105 1.443假定，经过前六次迭代后已满足收敛精度要求，则得α*=(a+b)/2=（0.558+1.443）/2=1.0005相应的函数极值:f（α*）=3.000001运用MATLB程序求解:建立m文件：function[x,minf]=minHJ(f,a,b,k) format long;if nargin==3eps=0.000001;enda1=b-0.618*(b-a);a2=a+0.618*(b-a);k=1;tol=b-a;while tol>eps&&k<100000fa1=subs(f,findsym(f),a1);fa2=subs(f,findsym(f),a2);if fa1>fa2a=a1;a1=a2;a2=a+0.618*(b-a);else b=a2;a2=a1;a1=b-0.618*(b-a);endk=k+1;tol=abs(b-a);endif k==100000disp('找不到最小值');x=NaN;minf=NaN;return;endkx=(a+b)/2minf=subs(f,findsym(f),x)format short函数文件：syms x;f=(x^2-1)^2+(x-1)^2+3;[x,minf]=minHJ(f,-10,10);运行结果:k=36k=36x=1.000004289112507 minf=3.000000000091983。

分金块问题的解决思想和算法设计王雕40912127 2009级计算机科学与技术三班摘要：在日常生活中，分金块问题是一个常见的问题，人们总是会面临怎样比较大小。

本文给出了较为常用的两种算法—蛮力法和分治法。

关键词：分金块问题；蛮力法(非递归)；分治法；1 问题概述老板有n个金块，希望最优秀的雇员得到其中最重要的一块，最差的雇员得到其中最轻的一块。

假设有一台比较重量的仪器，如何用最少的比较次数找出最重和最轻的金块？2 理解金块问题：以9以内的实例理解问题金块示例问题：1.最重的是那块？用max标记2.最轻的是那块？用max标记3 求解金块问题的常用算法一蛮力法蛮力法的设计思想：蛮力法，也称穷举法，是一种简单而直接地解决问题的方法，常常直接基于问题的描述，因此，也是最容易应用的方法。

但是，用蛮力法设计的算法其时间性能往往是最低的，典型的指数时间算法一般都是通过蛮力搜索而得到的。

即从第一块开始查找，查找哪块最重，哪块最轻。

a[0] a[1] a[2] a[3]max4算法设计：Maxmin(float a[],int n){max=a[1];min=a[1];for(i=2;i<=n;i=i+1){if(max<a[i])max=a[i]else if(min>a[i])min=a[i]}Return(max, min)}Step1 将所有金块重量存于数组Step2 将第一个金块同时标记为最重和最轻的金块Step3 将第一个与后一个进行重量的比较，将更重的标记为max，同时如果现阶段最轻的比后者轻，那么将后者标记为min。

Step4 依次进行比较，最重得到最重的和最轻的max min.5算法分析：(1)时间复杂性和空间复杂性。

分析该算法可以看出，比较操作max<a[i]和mix<a[i]是执行频次最高的关键语句。

因此以这两个语句执行的总次数作为该算法执行所需要的时间。

最好情况下，金块由轻到重排列，不需要进行min<a[i]比较，而max<a[i]比较共需进行n-1次,即可得到max和min; 最坏情况下，金块由重到轻排列，还需要进行n-1次min<a[i]比较，才能得到最终的min，因此共进行2(n-1)次比较。

二，框图：
2
开始
给定 a, b, ε
λ ←0.618
a1←b-λ (b-α ) a2←b+λ (b-α )
y1←f(a1) y2←f(a2)
是 y1≧y2?
否
a←a1 a1←a2 y1←y2
b←a2 a2←a1 y2←y1
a2←a+λ (b-α ) y2←f(a2)
a1←b-λ (b-α ) y1←f(a1)
是
|
ba |<ε b
和|
y1 y 2 |<ε y2
否
a3←
1 (a+b) 2
3
结束
三，程序： #include<stdio.h> #include<math.h> #define E 1e-3 int main() { double a=-3.0,b=5.0,y=0.618; int N=0; double a1,a2,y1,y2,a3; a1=b-y*(b-a); a2=a+y*(b-a); y1=a1*a1+2*a1; y2=a2*a2+2*a2; while(1) { N++; printf("第%d 次迭代\t",N); if(y1>=y2) { a=a1; a1=a2; y1=y2; a2=a+y*(b-a); y2=a2*a2+2*a2; printf("a=%.3lf\t a1=.3lf%\t a2=%.3lf\t b=%.3lf\t y1=.3lf%\t y2=.3lf%\t\n",a,a1,a2,b,y1,y2); } else { b=a2; a2=a1; y2=y1; a1=b-y*(b-a); y1=a1*a1+2*a1; printf("a=%.3lf\t a1=%.3lf\t a2=%.3lf\t b=%.3lf\t y1=%.3lf\t y2=%.3lf\t\n",a,a1,a2,b,y1,y2); } if((fabs((b-a)/b)<E)&&(fabs((y2-y1)/y2)<E)) { a3=(a+b)/2; printf("迭代终止最后精确值 a3=%.3lf\t f(a3)=%.3lf\n",a3,a3*a3+2*a3); break; } else continue; } return 0; }

算法设计与分析答案屈婉玲【篇一：分金块问题的解决思想和算法设计】s=txt>摘要：在日常生活中，分金块问题是一个常见的问题，人们总是会面临怎样比较大小。

才能利用一种最高效的算法选出其中最大和最小的金块。

本文给出了较为常用的两种算法—蛮力法和分治法。

关键词：分金块问题；蛮力法(非递归)；分治法；points gold bullion problem solving thought and algorithm designabstract: in daily life, points gold bullion is a common problem, people will always face how to compare size. can use one ofthe mostefficient algorithm choose the maximum andminimum of the gold. this paper gives a more commonly used two kinds of algorithm, brute force method and partition method.keywords: points gold bullion problem; brute forcemethod(non recursive); partition method;1引言递归调用是一种特殊的嵌套调用，是某个函数调用自己，而不是另外一个函数。

递归调用一种解决方案，一种是逻辑思想，将一个大工作分为逐渐减小的小工作，比如说一个和尚要搬50块石头，他想，只要先搬走49块，那剩下的一块就能搬完了，然后考虑那49块，只要先搬走48块，那剩下的一块就能搬完了……，递归是一种思想，只不过在程序中，就是依靠函数嵌套这个特性来实现了。

由于回溯法是对解空间的深度优先搜索，因此在一般情况下可用递归函数来实现回溯法2问题概述老板有n个金块，希望最优秀的雇员得到其中最重要的一块，最差的雇员得到其中最轻的一块。

一、什么叫优选法 （3）优选法： 利用数学原理，合理安排试验， 以最少的试验次数迅速找到最佳 点，从而解决优选问题的科学试 验方法。
二、单峰函数
（1）单峰函数的定义中有两个要点：
①f(x)在［a,b］上只有唯一 的最大 （小）值C。
② f(x)在［a,C］上递增（减），在
［C,b］上递减（增）。
二、单峰函数
（2）单峰函数的定义：
如果f(x)在［a,b］上只有唯一 的最大 （小）值点C，而f(x)在［a,C］上递增 （减），在［C,b］上递减（增）。则 称f(x)为区间［a,b］上的单峰函数。
规定：区间［a,b］上的单调函数也是 单峰函数。
三、黄金分割法---0.618法
1. 黄金分割常数
段，留下存优范围[a1, b1]，显然有[a1, b1] [a, b]；再在[a1, b1]内任选两点各做一次
试验，并与上次的好点比较，确定新的好
点和新的差点，并在新的差点处把[a1, b1]
分成两段，截掉不包含新好点的那段，留
下新的存优范围[a2, b2]，同样有[a2, b2] [a1, b1]… …重复上述步骤，可使存优范围 逐步缩小.
较好，则去掉1382克以下部分．假定试验结果 第一点较好，那么去掉1382克以下的部分，即 存优范围为[1382，2000]，在此范围找出第一 点(即1618)的对称点做第三次试验.其加入量用 公式计算：加入量=大+小－中.即第三次试验 的加入量为：2000+1382－1618=1764(g). ④再将第三次试验结果与第一点比较，如 果仍然是第一点好些，则去掉1764克以上部分， 如果第三点好些，则去掉1618克以下部分.假设 第三点好些，则在留下部分(即[1618, 2000])找 出第三点(即1764)的对称点做第四次试验.第四 点加入量为：2000－1764+1618=1854(g).

一维搜索方法的MATLAB 实现__ __信息与计算科学__ 实验时间: 2014/6/21一、实验目的：通过上机利用Matlab 数学软件进行一维搜索，并学会对具体问题进行分析。

并且熟悉Matlab 软件的实用方法，并且做到学习与使用并存，增加学习的实际动手性，不再让学习局限于书本和纸上，而是利用计算机学习来增加我们的学习兴趣。

二、实验背景： 黄金分割法它是一种基于区间收缩的极小点搜索算法，当用进退法确定搜索区间后，我们只知道极小点包含于搜索区间内，但是具体哪个点，无法得知。

1、算法原理黄金分割法的思想很直接，既然极小点包含于搜索区间内，则可以不断的缩小搜索区间，就可以使搜索区间的端点逼近到极小点。

2、算法步骤用黄金分割法求无约束问题min (),f x x R ∈的基本步骤如下：〔1〕选定初始区间11[,]a b 与精度0ε>，计算试探点：11110.382*()a b a λ=+-11110.618*()a b a μ=+-。

〔2〕若k k b a ε-<，则停止计算。

否则当()()k k f f λμ>时转步骤〔3〕。

当()()k k f f λμ≤转步骤〔4〕。

〔3〕11111110.382*()k k k k k kk k k k a b b a b a λλμμ+++++++=⎧⎪=⎪⎨=⎪⎪=+-⎩转步骤〔5〕〔4〕转步骤〔5〕（5）令1k k =+，转步骤〔2〕。

算法的MATLAB 实现function xmin=golden(f,a,b,e)k=0;x1=a+0.382*(b-a);x2=a+0.618*(b-a);while b-a>ef1=subs(f,x1);f2=subs(f,x2);if f1>f2a=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);elseb=x2;x2=x1;f2=f1;x1=a+0.382*(b-a);endk=k+1;endxmin=(a+b)/2;fmin=subs(f,xmin)fprintf('k=\n');disp(k);3、实验结果(总结/方案)黄金分割法求解极值实例。

实验报告课程名称：机械优化设计实验项目：一维搜索(黄金分割)法上机实验专业班级： XXXXX级机械工程及自动化XX班学号： XXXXXXXXXX 姓名： XXXXXX 指导老师： XXXXXX 日期： 201X.12.12机械工程试验教学中心实验1 一维搜索(黄金分割)法实验报告实验日期 201X 年 12 月 11 日报告日期 201X 年 12 月 12 日班级 XXXXX级机自XXXX班姓名 XXXXXX 学号 XXXXXXXXXXXXXXX1、实验目的○1了解黄金分割法的基本原理；○2熟悉matlab程序使用方法；○3学习上机调试、运行所编写的程序。

2、黄金分割法原理该法适用于[a,b]区间上单谷函数极小值问题。

在搜索区间[a,b]内按照0.618比例加入两点α1,α2，并计算其函数值。

α1,α2将区间分成三段，然后利用区间消去法，通过比较函数值大小，删除其中一段，使搜索区间缩短，在保留区间进行同样处理，直到搜索区间缩小到指定精度为止。

3、编制MATLAB优化程序○1编写函数文件，并命名为fx.m保存，程序代码如下：function f=fx(w)%f=w^2-10*w+36;%f=w^4-5*w^3+4*w^2-6*w+60;%f=((w+1)^4)*((w-2)^2);注：上述“%”后面分别为要求解的三个方程，求解该方程式把相应方程式前面的“%”删除，点击保存，并运行下面的hjf.m文件，输入相应的初始步长h0、初始点x0、收敛法则epsilan的值○2编写进退法程序文件，命名为ab1.m保存，程序代码如下：function [a,b]=ab1(h0,x0)h=h0;x1=x0;f1=fx(x1);x2=x1+h;f2=fx(x2);if f2>f1h=-h;x3=x1;f3=f1;x1=x2;f1=f2;x2=x3;f2=f3;endx3=x2+h;f3=fx(x3);while f2>=f3x1=x2;f1=f2;x2=x3;f2=f3;x3=x2+2*h;f3=fx(x3);endif h<0a=x3;b=x1;elsea=x1;b=x3;end○3编写黄金分割法程序文件，命名为hjfgf.m 保存，程序代码如下： function hjfclearh1 = input('h0=?');x1=input('x0=?');epsilan=input('epsilan=?');[a,b]=ab1(h1,x1);x1=a+0.382*(b-a);f1=fx(x1);x2=a+0.618*(b-a);f2=fx(x2);while abs(b-a)>epsilanif f1>f2a=x1;x1=x2;f1=f2;x2=a+0.618*(b-a);f2=fx(x2);elseb=x2;x2=x1;f2=f1;x1=a+0.382*(b-a);f1=fx(x1);endendxm=(a+b)/2;['Optimal result:',blanks(3),'xm=[',...num2str(xm),']',blanks(6),'fm=',num2str(fx(xm))]4、实验结果()3610min )12+-=t t t f结果: *t = 5.0001 =*f 11 （h0=0.3、x0=0、epsilan=0.001）()60645min )2234+-+-=t t t t t f结果: *t = 3.2795 =*f 22.659 （h0=0.3、x0=0、epsilan=0.001）()()()2421min )3-+=t t t f 结果: *t =__-0.99989__ =*f __1.4253e-015__ （h0=0.3、x0=0、epsilan=0.001）。

贪⼼算法-⾦条切割问题题⽬：⼀块⾦条切成两半，是需要花费和长度数值⼀样的铜板的。

⽐如长度为20的⾦条，不管切成长度多⼤的两半，都要花费20个铜板。

问：⼀群⼈想整分整块⾦条，怎么分最省铜板？例如，给定数组{10，20，30}，代表⼀共三个⼈，整块⾦条长度为10+20+30=60。

⾦条要分成10，20，30。

如果先把长度60的⾦条分成10和50，花费60；再把长度50的⾦条分成20和30，花费50；⼀共花费110铜板。

但是如果先把长度60的⾦条分成30和30，花费60；再把长度30⾦条分成10和20，花费30；⼀共花费90铜板。

输⼊⼀个数组，返回分割的最⼩代价。

solution：1、准备⼀个⼩根堆2、把所有树放到⼩根堆中3、然后依次弹出两个数，求和4、把和扔到⼩根堆中循环3、4步骤代码：package Algorithms.greed;import java.util.PriorityQueue;public class LessMoneySplitGold {public static int lessMoney(int[] arr) {PriorityQueue<Integer> pQ = new PriorityQueue<>(); //1、准备⼀个⼩根堆for (int i = 0; i < arr.length; i++) { //2、把所有数字扔到⼩根堆中pQ.add(arr[i]);}int sum = 0;int cur = 0;while (pQ.size() > 1) {cur = pQ.poll() + pQ.poll(); //3、每次弹出两个数字进⾏结合sum += cur;pQ.add(cur); //4、把结合的数扔到⼩根堆中}return sum;}public static void main(String[] args) {// solutionint[] arr = {6, 7, 8, 9};System.out.println(lessMoney(arr)); //60}}package Algorithms.greed;import java.util.Arrays;import parator;import java.util.LinkedList;import java.util.PriorityQueue;public class LessMoneySplitGold {public static int lessMoney(int[] arr) {//1、准备⼀个⼩根堆//PriorityQueue<Integer> pQ = new PriorityQueue<>();Arrays.sort(arr);LinkedList<Integer> q = new LinkedList<>();for (int i = 0; i < arr.length; i++) { //1、把所有数字扔到⼩根堆中q.add(arr[i]);}int sum = 0;int cur = 0;while (q.size() > 1) {cur = q.poll() + q.poll(); //2、每次弹出两个数字进⾏结合System.out.println(cur);sum += cur;q.add(cur); //3、把结合的数扔到⼩根堆中}return sum;}//⽐较器构建⼩根堆public static class MinheapComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o1 - o2; // < 0 o1 < o2 负数}}//⽐较器构建⼤根堆public static class MaxheapComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1; // < o2 < o1}}public static void main(String[] args) {// solutionint[] arr = { 6, 7, 8, 9 };System.out.println(lessMoney(arr)); // 60int[] arrForHeap = { 3, 5, 2, 7, 0, 1, 6, 4 };// min heapPriorityQueue<Integer> minQ1 = new PriorityQueue<>();for (int i = 0; i < arrForHeap.length; i++) {minQ1.add(arrForHeap[i]);}while (!minQ1.isEmpty()) {System.out.print(minQ1.poll() + " "); //0 1 2 3 4 5 6 7}System.out.println();// min heap use ComparatorPriorityQueue<Integer> minQ2 = new PriorityQueue<>(new MinheapComparator());for (int i = 0; i < arrForHeap.length; i++) {minQ2.add(arrForHeap[i]);}while (!minQ2.isEmpty()) {System.out.print(minQ2.poll() + " "); //}System.out.println();// max heap use ComparatorPriorityQueue<Integer> maxQ = new PriorityQueue<>(new MaxheapComparator());for (int i = 0; i < arrForHeap.length; i++) {maxQ.add(arrForHeap[i]);}while (!maxQ.isEmpty()) {System.out.print(maxQ.poll() + " ");}}}/*** 13* 17* 30* 60* 0 1 2 3 4 5 6 7* 0 1 2 3 4 5 6 7* 7 6 5 4 3 2 1 0*/⼤根堆、⼩根堆的构建。

实验一黄金分割法一、实验目的　１、加深对黄金分割法及其算法框图与步骤的理解。

　２、培养学生独立编制、调试黄金分割法Ｃ语言程序的能力。

　３、掌握常用优化方法程序的使用方法。

　４、培养学生灵活运用优化设计方法解决实际工程问题的能力。

　二、实验内容　１、编制调试黄金分割法Ｃ语言程序。

　２、利用调试好的Ｃ语言程序进行实例计算。

　３、根据实验结果写实验报告。

　三、实验步骤　１、编制调制程序。

　２、计算实例。

　四、算法及框图　计算实例：被搜索函Ｆ（ｘ）＝ｘ４－４ｘ３－６ｘ２－１６ｘ＋４　步骤一：？？ｍａｔｌａｂ？？⒉⒌？Ｆ（ｘ）？？兎？ㄅ？⒉？枽？？ⅴ？？洛？ㄞ？扟嫛兢？？？？？　　步骤二：？？？？？？？侱？梃［ｘ１，ｘ２］；　步骤三：？？煓摠⒕━？？⒉？？屲＊ｐ　①外推法部分的程序框图　　②黄金分割法部分的程序框图　③外推法与黄金分割法合起来后的总程序　#include <stdio.h>#include <math.h>#define e 0.00001 /*设定黄金分割的精度值为为e=0.00001*/#define tt 0.00000001 /*设置外推法的最初步长为h=0.00000001*/float f(double x) /*定义被搜索函数f（x）*/{float y=pow(x,4)-4*pow(x,3)-6*pow(x,2)-16*x+4;return(y); /*返回函数计算值f(x)*/}finding(float *p1,float*p2) /*使用指针方式定义确定搜索区间的外推法函数finding( ) */{float x1=0,x2,x3,t,f1,f2,f3,h=tt;int n=0;x2=x1+h;f1=f(x1);f2=f(x2);if(f2>f1) {h=-h;t=x2;x2=x1;x1=t;} /*若f2>f1，则反向搜索*/x3=x2+h;while(f(x3)<f(x2)){ h=2*h;x1=x2;f1=f(x2);x2=x3;f2=f(x3);x3=x2+h;n=n+1;}if(x1>x3){t=x1;x1=x3;x3=t;}*p1=x1;*p2=x3; /*利用指针*p1、*p2向主函数返回搜索区间的始点a、终点b的值，即a=*p1=x1，b=*p2=x2 */return(n); /*向主函数返回使用外推法时的循环次数n */}gold(float *p) /*使用指针方式定义确定最小值点的黄金分割函数gold( ) */{float a,b,x1,x2,f1,f2;int n=0;finding(&a,&b); /*利用指针的方式，通过函数finding( )确定确定搜索区间的始点a、终点b 的值*/do{x1=a+0.382*(b-a);x2=a+0.618*(b-a);f1=f(x1);f2=f(x2);n=n+1;if(f1>f2) a=x1;else b=x2;}while((b-a)>e); /*通过黄金分割的方法缩小最优点所在的区间直到满足精度要求e为止*/*p=(a+b)/2; /*取最小区间的中点作为极小值点的数值*p */return(n); /*返回使用黄金分割法时迭代的次数n */}void main() /*主函数部分*/{float a,b,x,min;int n1,n2;n1=finding(&a,&b); /*利用指针方式，通过调用确定搜索区间的外推法函数finding( ),确定搜索区间的始点a、终点b的值，并确定使用外推法时的循环次数n1*/n2=gold(&x); /*利用指针方式，通过调用黄金分割函数gold( )，确定极小值点的数值x，并确定使用黄金分割法时迭代的次数n2*/min=f(x); /*通过调用被搜索函数f(),计算最小点的函数值min */printf("\n 被搜索函数是F(x)=x^4-4x^3-6x^2-16x+4,精度为e=0.00001");printf("\n 利用外推法确定的搜索区间是: [%f, %f]",a,b);printf("\n 用外推法确定搜索区间时的循环次数是: n1=%d 次",n1);printf("\n 在搜索区间内使用黄金分割法的迭代次数是: n2=%d 次",n2);printf("\n 产生极小值点是在: x=%f 处,并且极小值是: F(%f)=%f",x,x,min);printf("\n");｝　程序运行结果：　五、实验结果分析：　 从上面的程序运行结果和利用Ｍａｔｌａｂ解出的结果相比较，利用外推法和黄金分割法求函数的最优解可以达到很高的精度值，和精确解的误差相差很小，并且这种方法对函数除要求“单谷”外不做其他要求，而且函数可以不连续，因此，该方法的适应面相当广。