下载文档原格式
1.数阵图类型发射型：封闭型2.突破方法：①找数字出现最多的线，用加减法去算②头中尾，填中间，大小大小手拉手3.数阵图歌数阵图，真有趣，每条线，和相等数越多，先找他，头中尾，中间填1.在图中空格里填上一个数，使得横行、竖行的三个数的和等于10.8简单数阵知识点：2.在图中空格里填上一个数，使得横行、竖行的三个数的和等于9.3.在图中空格里填上一个数，使得横行、竖行的三个数的和等于9.4.把4、5、7、8四个数填在四个空格里，使得横行、竖行三个数相加等于18.5.在圆圈里填上合适的数，使每条线上三个数的和都等于10.6.在正方形中填上合适的数，使横行、竖行、斜行上的三个数相加都等于18.7.把数字1、2、3、4、6、7、8、9分别填入下面八个圆圈中，使每条线上的三个数字的和等于15.8.把1、2、3、4、5这五个数填入图中的方格中，使横行、竖行三个数的和都相等.9.把1、2、3、4、5这五个数填入图中的方格中，使横行、竖行三个数的和都等于9.10.把1、2、3、4、5、6、7这七个数填入下面的圆中，使每条线上的三个数相加都相等.11.把1、2、3、4、5、6、7这七个数填入下面的圆中，使每条线上的三个数相加和都等于14.12.把2、3、4、5、6、7、8这七个数填入下面的圆中，使每条线上的三个数和都等于15.13.把4、6、9、11这四个数分别填入下图的圆圈中，使每条线上及大圆圈上的各数相加和都相等.14.把5、5、7、7、9、9分别填在下面的圆圈里，使每条边上都有5、7、9.1.填数，使横行、竖行的三个数相加都得11. (2)填数，使每条线上的三个数之和都得15.2.在圆圈里填上合适的数，使每条线上三个数的和都等于8.3.要使表格中每行、每列和两条对角线上的三个数的和都为18，下面每个方框里应填什么数？4.在下列两图的空格中填上数，使横行和竖行或每条对角线上的三个数相加都等于15.5.在下面的○里填上适当的数，使每条线上的三个数之和都是12.6.把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数相加都得15.7.把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于1 2.8.把3，4，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为20.9.把4、6、9、11这四个数分别填入下图的圆圈中，使每条线上及大圆圈上的各数相加和都相等.10.在每个方格内，只能填1、2、3三个数字，使横行、竖行的三个数相加都相等，但每一横行、竖行的三个数字互不相同.54、634和8,5和7随便填1.相邻数加法和减法的特征：①加法特征：大小、大小和相等，是横式变形的根本.②减法特征：相邻两数相减，差永远是1.（减法相等的依据）③根据等式是天平，可以左右加减同一个数（等式重要性质）2.重要方法： ①找特殊：对于多个式子，有些式子的填法很多（不作为突破点），要学会寻找填法较少或者唯一的作为突破点；②分组法：几个连续数的“和”填式子，找中间数3.不等式填数，先假设是等式，然后根据要求填写合适的数.4.当你不会做题的时候，往数学方法靠近，千万不可“胡猜乱想”：①学习方法第一位 ②多看看前面的笔记，帮助自己理解1.把3、4、5、6这四个数填入下面的算式中，使等式成立.（每个算式中，同一个数只能用一次）（1）（ ）+（ ）=（ ）+（ ）（2）（ ）+（ ）-（ ）=（ ）（3）（ ）-（ ）+（ ）=（ ）9横式填数知识点：2.把1、2、3、4、5、6、7、8这8个数分别填入下面的方框里（每个数只能用一次），使等式成立.3.把4、5、6、7、9、13分别填入下面的中（每个数只能用一次），使等式成立．4.将0、1、2、3、7、8、9填入下面的方格内，使算式成立.5.把2、3、4、6、7、9分别填入下面6个圆圈中，使3个算式成立.6.在下面括号里填入适当的数.（）-9＞26+7 （2）（）-12＜10+207.把1～10这十个数填入横线中，使等式成立．（每个数只能用一次）8.智力擂台．（1）把0、1、2、3、4、5按要求填在方格里，每个数只能用一次．□-□=□-□=□-□如果是加法算式，又可以怎样填呢？□+□=□+□=□+□（2）数学谜语．像个蛋，不是蛋；说它圆，不太圆；说它没有它又有，十、百、千、万连成串．猜一数字．9.把1、2、3、6、7、8、9分别填入□中，使算式成立：10.用2、3、4、5、6、7、8、9这八个数编出下面两道加减混合算式（每个数只能用一次）．11.在括号里填入合适的数，使不等式成立.15+3＞（） 27-（）＞26-7 9+（）＜（）1.用26、27、28、29四个数值编三道加减混合算式．（每个算式中每个数只能用一次）（1）（）+（）=（）+（）（2）（）+（）-（）=（）（3）（）-（）+（）=（）2.把0、1、2、3、7、8、9分别填入□中，使算式成立：3.把3、4、5、6、32、33、34、35这8个数填入下面的两个算式中，使等式成立.4.在5、6、7、8、9、10、11中选择6个数填入下面的算式，使等式成立.（）+（）=（）+（）=（）+（）（）-（）=（）-（）=（）-（）5.括号里最小能填几?（）-4＞7+2 26-（）＜9+146.用2、4、5、6、7和10组成加减两个算式（每个数字只能使用一次）.（）+（）=（）（）-（）=（）7.从1——9这九个数中选出4个数进行组合，使他们相加的和是100.8.把1～10这十个数填入横线中，使等式成立．（每个数只能用一次）参考答案：课堂共同学习1.（1）3+6=4+5 （2）3+6-4=5 （3）5-3+4=6（答案不唯一：核心借助3+6=4+5）2.1+8-7=2,3+6-4=5（答案多多，核心借助大小大小和相等）3.①6+7=13，②9-5=44.8+9=20-3=17（突破点：中间第一个必然为2，最后一个首位必然是1）5.3+7=10,9-4=5，2+6=8（突破点：只有2+6=8）6.43,41（最小和最大填法）7.（突破点在最后一个）8.（1）5-4=3-2=1-0 （2）0+5=1+4=2+3 （3）09.8+9=23-6=1710.2+9-8=3， 7-5+4=6（答案多多）11.略课后自我提升：1.（1）26+29=27+28 （2）26+29-27=28 （3）28-26+27=292.8+9=20-3=173.3+35-4=34 5+33-6=324.5+11=6+10=7+9 6-5=8-7=10-95.14 、 46.5+2=7 10-4=67.32+68=1008.略1.填符号核心理念：看得数，变少了，找减号，变多了，找加号.2.对于相同数字填符号：如4 4 4 4 = 0（运用组合法靠近要求的结果）三种组合：①单个为4 ②4+4=8 ③4-4=03.对于相邻位置凑数字：①找靠近结果的数字组合 ②剩下的按照加减去推断如：1 2 3 4 5 =33，优先考虑23结合1.在○中填上适当的符号.（选择填“＞、＜、=、＋、或－”）.13○10 8○10 15○9+6 18-7○1115○5=20 19○2○8=9 20○0=10○10 11○3○5=92.将1、2、3、4、5、6、7、8分成和相等的四组填入下面的方格中.3.将1、2、3、4、5、6、7、8分成和相等的两组组填入下面的方格中.4.在四个4中间填上“+、-”号，使算式成立.（写出三种不同的填法）4 4 4 4 = 04 4 4 4 = 04 4 4 4 = 010巧填符号知识点：5.在下面的方格中填入适当的数，使相邻三个数相加的和都是10.6.在数字之间添上“十”号，位置相邻的两个数字可以组成一个数．5 6 7 8 9 = 98．7.在下图五个2中间填上“+、-”号，使算式成立.（写出三种不同的填法）2 2 2 2 2 = 22 2 2 2 2 = 22 2 2 2 2 = 28.在方格里填上合适的数，使等式成立.（1）9=□+2+3（2）□=□-4-1（3）8-□=□+59.在下面的数字间填上“+、-”号，使算式成立.（位置相邻的数字可以组成一个数）1 2 3 4 5 = 51 2 3 4 5 = 241 2 3 4 5 = 610.在六个8之间填上加减号，使等式成立（提示位置相同的数字可以组成一个数）8 8 8 8 8 8=8811.在1、3、5、7、9之间填上“＋或-”（位置相邻的数可以组成一个数），使等式成立.1 3 5 7 9 =7912.在合适的地方填写“＋或-”，使等式成立.1 2 3 4 5 6=11.在四个5之间填上“＋或-”，使等式成立.5 5 5 5 = 02.在合适的地方填写“＋或-”，使等式成立.1 2 3 4 5 = 73.在所给的已知数之间，填上“＋或－”使等式成立.（1）8 4 3 = 9 （2）5 6 3 = 8（3）7 2 1 = 8 （4）9 5 2 = 64.在下列各数之间填上“＋或-”（相邻数可以组成一个数），使他们结果为10.2 2 2 1 1 1 = 105.在○中填入“＋或-”，使等式成立.（1）8○9=19○2 （2）30○15=9○6（3）3○8=14○3 （4）20○20=17○176.在1、2、3、4、5之间填上“＋”（位置相邻，可以组成一个数），使他们和等于33.1 2 3 4 5 =337.在6个6之间填上“+或-”，使下面的等式成立.6 6 6 6 6 6=0 6 6 6 6 6 6=12参考答案：课堂共同学习：（部分有答案）5.依次是：63163163166.5+6+78+9=98．8.（1）4；（2）多种答案如：5、10；（3）多种答案如：0、3和1、211.13+57+9=7912.1+2+3-4+5-6=1课后自我提升：（部分有答案）2.1+2+3-4+5=74.22-2-11+1=106.1+23+4+5=331.组合问题：按照从左往右的顺序先固定一个，然后交换后面的位置，或者和后面的每一个都结合.2.搭配问题：①标号码 ②画线条 ③数数量（加法思维）3. 简单的数码分类方法：①在个位：从1数到60，个位有6个2②在十位：从1数到60，十位只有20——29有10个24.培养学生严谨的顺序思维，做到不重复和不遗漏.1.用8、3、0三个数字可以组成多少个不同的三位数？2.用彩带装饰草帽，有3顶不同颜色的草帽和3条不同颜色的彩带，你知道有几种不同的搭配方式吗？11搭配组合知识点：3.10个小朋友要分两伙做游戏，一共有几种不同的分法？4.某人数数，他从一开始，按照1、2、3、4…的顺序一直数到22，他一共数了几个1，几个2？5.小芳与3个小朋友见面，互相握手问好，一共要握几次手？6.中午学生食堂供应主食3种：米饭、馒头、面条，菜4种：青菜、鱼、牛肉、鸡肉.小红到食堂吃饭，主食和菜各挑选一份，她一共有几种不同的选法？7.用7、2、1三个数字可以组成多少个不同的三位数？8.老师有2件不同款式的上衣，有3条不同颜色的裤子，你知道老师能搭配出几种不同的穿着方式吗？9.星星面前有一盘花生米，他“1、2、3、4、5.....”一个一个的往下数，一直数到35.星星一共数了几个5，一共数了几个2？10.4个人下围棋，每两个人下一盘围棋，一共下了几盘围棋？11.明明有一个5分硬币，4个2分硬币，8个1分硬币，要组成8分，共有几种不同的搭配方法？12.从小力、小红、小新、小芳4人中挑选2位同学参加小记者选拔比赛，一共有几种不同的选法？1.王阿姨有2件不同颜色的上衣和3条不同款式的裤子．一件上衣搭配一条裤子，一共有多少种不同的搭配方法？2.小冉有3条不同款式的裙子，5双不同款式的靴子，某日她要去参加聚会，若穿裙子和靴子，则不同的穿着搭配方式的种数为（） A．7 B．8 C．153.用9、0、5三个数字，可以组成多少个不同的三位数？4.课间时间到了，学校为同学们准备的点心有4种：饼干、面包、薯条、蛋挞；准备的饮料有3种：果汁、牛奶、酸奶.每位同学可以任意选择一种点心和一种饮料，请问有几种不同的选择方法？5.红、黄、绿三种颜色可以组成不同的信号方式，有几种不同的信号方式？6.甜甜学数数：1、2、3、4、…一个接一个地往下数，一直数到45，她一共数了（）个含有数字5的自然数．7.用2，3，4三个数字可以组成多少个不同的三位数？写出并从小到大排列．8.从A、B、C、D四位同学中任选2人参加学校演讲比赛，一共有几种不同的可能性？并列举各种可能的结果．参考答案：课堂共同练习：1.4个2.9种3.5种4.13个1，6个25.6次6.12种7.6个8.6种9.4个5,14个210.6盘11.7种12.6种课后自我提升：1.6种2.C3.4个4.12种5.6种6.5个7.一共有6个；从小到大排列为：234＜243＜324＜342＜423＜4328.一共有6种不同的可能性，分别是：AB，AC，AD，BC，BD，CD．1.学习树状加法图：2.标号→画线→数数进行相加2.从学校经过书店到小明家共有几条路可走？请写出来．12路线问题知识点：3.小猫要回家，它可以有几种不同的走法？4.从甲地到乙地有3条路，从乙地到丙地有4条路，那么从甲地经过乙地到丙地有几种走法？5.一只蜜蜂，从“1”爬到“6”处，有几种不同的走法？6.小蚂蚁从1走到5，不走重复路，有几种不同的走法？7.小明、小红、小强、小莉是好朋友，这天他们每两人互通了一次电话。
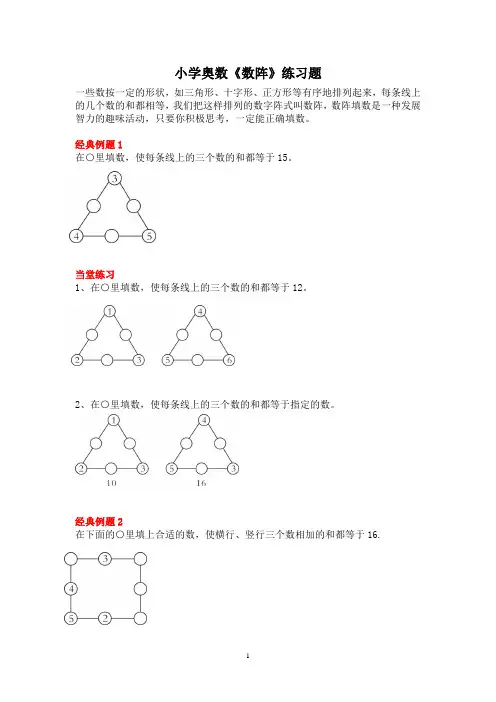
小学奥数《数阵》练习题一些数按一定的形状，如三角形、十字形、正方形等有序地排列起来，每条线上的几个数的和都相等，我们把这样排列的数字阵式叫数阵，数阵填数是一种发展智力的趣味活动，只要你积极思考，一定能正确填数。
经典例题1在○里填数，使每条线上的三个数的和都等于15。
当堂练习1、在○里填数，使每条线上的三个数的和都等于12。
2、在○里填数，使每条线上的三个数的和都等于指定的数。
经典例题2在下面的○里填上合适的数，使横行、竖行三个数相加的和都等于16.当堂练习1、填数，使每条线上三个数的和都等于指定的数。
2、填数，使横行、竖行的三个数相加的和都等于指定的数。
3、填数，使横行、竖行、斜行的三个数相加的和都等于12。
经典例题3将3，4，5，6，7这5个数填入图中5个圆圈里，使每条斜线上的3个数相加之和都是15。
当堂练习1、把1，2，3，4，5这5个数填在下面的圆圈里，使每条直线上3个数相加的和都等于10。
2、把2、3、4、5、6这5个数填在下面的方框中，使横行、竖行上三个数的和都等于指定的数。
3、把1～7这7个数填在下图7个圆圈里，使每条线上3个数相加的和都等于12。
经典例题4把2，3，4，5，6，7这六个数填在下面的六个圆圈里（每个数只能用一次），使每条直线上的三个数相加的和都等于12。
当堂练习1、把1，2，3，4，5，6这六个数填在下面的六个圆圈里（每个数只能用一次），使每条直线上的三个数相加的和都等于中间方框里指定的数。
2、把2，3，4，5，6，7这六个数填在下面的六个圆圈里（每个数只能用一次），使每条直线上的三个数相加的和最大且相等，该怎样填？经典例题51、在○里填数，使每条线上的三个数的和都等于指定的数。
2、在下面的“○”里填上合适的数，使每条线上的三个数的和都等于指定的数。
3、填数，使横行、竖行、斜行的三个数相加的和都等于15。
4、把1，3，5，7，9这5个数填在下面的圆圈里，使每条直线上3个数相加的和都等于指定的数。
1.数阵图类型 发射型：封闭型2.突破方法：①找数字出现最多的线，用加减法去算②头中尾，填中间，大小大小手拉手3.数阵图歌数阵图，真有趣，每条线，和相等数越多，先找他，头中尾，中间填10.9.3.在图中空格里填上一个数，使得横行、竖行的三个数的和等于9.4.把4、5、7、8四个数填在四个空格里，使得横行、竖行三个数相加等于18.5.在圆圈里填上合适的数，使每条线上三个数的和都等于10.6.在正方形中填上合适的数，使横行、竖行、斜行上的三个数相加都等于18.7.把数字1、2、3、4、6、7、8、9分别填入下面八个圆圈中，使每条线上的三个数字的和等于15.8.把1、2、3、4、5这五个数填入图中的方格中，使横行、竖行三个数的和都相等.9.把1、2、3、4、5这五个数填入图中的方格中，使横行、竖行三个数的和都等于9.10.把1、2、3、4、5、6、7这七个数填入下面的圆中，使每条线上的三个数相加都相等.11.把1、2、3、4、5、6、7这七个数填入下面的圆中，使每条线上的三个数相加和都等于14.12.把2、3、4、5、6、7、8这七个数填入下面的圆中，使每条线上的三个数和都等于15.13.把4、6、9、11这四个数分别填入下图的圆圈中，使每条线上及大圆圈上的各数相加和都相等.14.把5、5、7、7、9、9分别填在下面的圆圈里，使每条边上都有5、7、9.8简单数阵知识点：11. (2)填数，使每条线上的三个数之和都得15.2.在圆圈里填上合适的数，使每条线上三个数的和都等于8.3.要使表格中每行、每列和两条对角线上的三个数的和都为18，下面每个方框里应填什么数？4.在下列两图的空格中填上数，使横行和竖行或每条对角线上的三个数相加都等于15.5.在下面的○里填上适当的数，使每条线上的三个数之和都是12.6.把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数相加都得15.7.把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于1 2.8.把3，4，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为 20.9.把4、6、9、11这四个数分别填入下图的圆圈中，使每条线上及大圆圈上的各数相加和都相等.10.在每个方格内，只能填1、2、3三个数字，使横行、竖行的三个数相加都相等，但每一横行、竖行的三个数字互不相同.54、634和8,5和7随便填1.相邻数加法和减法的特征： ①加法特征：大小、大小和相等，是横式变形的根本.②减法特征：相邻两数相减，差永远是1.（减法相等的依据）③根据等式是天平，可以左右加减同一个数（等式重要性质）2.重要方法：①找特殊：对于多个式子，有些式子的填法很多（不作为突破点），要学会寻找填法较少或者唯一的作为突破点；②分组法：几个连续数的“和”填式子，找中间数9横式填数知识点：3.不等式填数，先假设是等式，然后根据要求填写合适的数.4.当你不会做题的时候，往数学方法靠近，千万不可“胡猜乱想”：①学习方法第一位②多看看前面的笔记，帮助自己理解.（每个算式中，同一个数只能用一（1）（）+（）=（）+（）（2）（）+（）-（）=（）（3）（）-（）+（）=（）2.把1、2、3、4、5、6、7、8这8个数分别填入下面的方框里（每个数只能用一次），使等式成立.3.把4、5、6、7、9、13分别填入下面的中（每个数只能用一次），使等式成立．4.将0、1、2、3、7、8、9填入下面的方格内，使算式成立.5.把2、3、4、6、7、9分别填入下面6个圆圈中，使3个算式成立.6.在下面括号里填入适当的数.（）-9＞26+7 （2）（）-12＜10+207.把1～10这十个数填入横线中，使等式成立．（每个数只能用一次）8.智力擂台．（1）把0、1、2、3、4、5按要求填在方格里，每个数只能用一次．□-□=□-□=□-□如果是加法算式，又可以怎样填呢？□+□=□+□=□+□（2）数学谜语．像个蛋，不是蛋；说它圆，不太圆；说它没有它又有，十、百、千、万连成串．猜一数字．9.把1、2、3、6、7、8、9分别填入□中，使算式成立：10.用2、3、4、5、6、7、8、9这八个数编出下面两道加减混合算式（每个数只能用一次）．11.在括号里填入合适的数，使不等式成立.15+3＞（） 27-（）＞26-7 9+（）＜（）29四个数值编三道加减混合算式．（每个算式中每个数只能用一次）（1）（）+（）=（）+（）（2）（）+（）-（）=（）（3）（）-（）+（）=（）2.把0、1、2、3、7、8、9分别填入□中，使算式成立：3.把3、4、5、6、32、33、34、35这8个数填入下面的两个算式中，使等式成立.4.在5、6、7、8、9、10、11中选择6个数填入下面的算式，使等式成立.（）+（）=（）+（）=（）+（）（）-（）=（）-（）=（）-（）5.括号里最小能填几?（）-4＞7+2 26-（）＜9+146.用2、4、5、6、7和10组成加减两个算式（每个数字只能使用一次）.（）+（）=（）（）-（）=（）7.从1——9这九个数中选出4个数进行组合，使他们相加的和是100.8.把1～10这十个数填入横线中，使等式成立．（每个数只能用一次）参考答案：课堂共同学习1.（1）3+6=4+5 （2）3+6-4=5 （3）5-3+4=6（答案不唯一：核心借助3+6=4+5）2.1+8-7=2,3+6-4=5（答案多多，核心借助大小大小和相等）3.①6+7=13，②9-5=44.8+9=20-3=17（突破点：中间第一个必然为2，最后一个首位必然是1）5.3+7=10,9-4=5，2+6=8（突破点：只有2+6=8）6.43,41（最小和最大填法）7.（突破点在最后一个）8.（1）5-4=3-2=1-0 （2）0+5=1+4=2+3 （3）0 9.8+9=23-6=1710.2+9-8=3， 7-5+4=6（答案多多）11.略课后自我提升：1.（1）26+29=27+28 （2）26+29-27=28 （3）28-26+27=292.8+9=20-3=173.3+35-4=34 5+33-6=324.5+11=6+10=7+9 6-5=8-7=10-95.14 、 46.5+2=7 10-4=67.32+68=1008.略1.填符号核心理念：看得数，变少了，找减号，变多了，找加号.2.对于相同数字填符号：如4 4 4 4 = 0（运用组合法靠近要求的结果）三种组合：①单个为4 ②4+4=8 ③4-4=03.对于相邻位置凑数字：①找靠近结果的数字组合 ②剩下的按照加减去推断 如：1 2 3 4 5 =33，优先考虑23结合.（选择填“＞、＜、=、＋、或－”）.10 15○9+6 18-7○1115○5=20 19○2○8=9 20○0=10○10 11○3○5=92.将1、2、3、4、5、6、7、8分成和相等的四组填入下面的方格中.3.将1、2、3、4、5、6、7、8分成和相等的两组组填入下面的方格中.4.在四个4中间填上“+、-”号，使算式成立.（写出三种不同的填法）4 4 4 4 = 010巧填符号知识点：4 4 4 4 = 04 4 4 4 = 05.在下面的方格中填入适当的数，使相邻三个数相加的和都是10.6.在数字之间添上“十”号，位置相邻的两个数字可以组成一个数．5 6 7 8 9 = 98．7.在下图五个2中间填上“+、-”号，使算式成立.（写出三种不同的填法）2 2 2 2 2 = 22 2 2 2 2 = 22 2 2 2 2 = 28.在方格里填上合适的数，使等式成立.（1）9=□+2+3（2）□=□-4-1（3）8-□=□+59.在下面的数字间填上“+、-”号，使算式成立.（位置相邻的数字可以组成一个数）1 2 3 4 5 = 51 2 3 4 5 = 241 2 3 4 5 = 610.在六个8之间填上加减号，使等式成立（提示位置相同的数字可以组成一个数）8 8 8 8 8 8=8811.在1、3、5、7、9之间填上“＋或-”（位置相邻的数可以组成一个数），使等式成立.1 3 5 7 9 =7912.在合适的地方填写“＋或-”，使等式成立.1 2 3 4 5 6=1-”，使等式成立.5 5 5 5 = 02.在合适的地方填写“＋或-”，使等式成立.1 2 3 4 5 = 73.在所给的已知数之间，填上“＋或－”使等式成立.（1）8 4 3 = 9 （2）5 6 3 = 8（3）7 2 1 = 8 （4）9 5 2 = 64.在下列各数之间填上“＋或-”（相邻数可以组成一个数），使他们结果为10.2 2 2 1 1 1 = 105.在○中填入“＋或-”，使等式成立.（1）8○9=19○2 （2）30○15=9○6（3）3○8=14○3 （4）20○20=17○176.在1、2、3、4、5之间填上“＋”（位置相邻，可以组成一个数），使他们和等于33. 1 2 3 4 5 =337.在6个6之间填上“+或-”，使下面的等式成立. 6 6 6 6 6 6=0 6 6 6 6 6 6=12参考答案：课堂共同学习：（部分有答案）6.5+6+78+9=98．8.（1）4；（2）多种答案如：5、10；（3）多种答案如：0、3和1、2 11.13+57+9=79 12.1+2+3-4+5-6=1课后自我提升：（部分有答案） 2.1+2+3-4+5=7 4.22-2-11+1=10 6.1+23+4+5=331.组合问题： 按照从左往右的顺序先固定一个，然后交换后面的位置，或者和后面的每一个都结合.2.搭配问题：①标号码 ②画线条 ③数数量（加法思维）11搭配组合知识点：3. 简单的数码分类方法：①在个位：从1数到60，个位有6个2②在十位：从1数到60，十位只有20——29有10个24.培养学生严谨的顺序思维，做到不重复和不遗漏.有3顶不同颜色的草帽和3条不同颜色的彩带，你知道有几种不同的搭配方式吗？3.10个小朋友要分两伙做游戏，一共有几种不同的分法？4.某人数数，他从一开始，按照1、2、3、4…的顺序一直数到22，他一共数了几个1，几个2？5.小芳与3个小朋友见面，互相握手问好，一共要握几次手？6.中午学生食堂供应主食3种：米饭、馒头、面条，菜4种：青菜、鱼、牛肉、鸡肉.小红到食堂吃饭，主食和菜各挑选一份，她一共有几种不同的选法？7.用7、2、1三个数字可以组成多少个不同的三位数？8.老师有2件不同款式的上衣，有3条不同颜色的裤子，你知道老师能搭配出几种不同的穿着方式吗？9.星星面前有一盘花生米，他“1、2、3、4、5.....”一个一个的往下数，一直数到35.星星一共数了几个5，一共数了几个2？10.4个人下围棋，每两个人下一盘围棋，一共下了几盘围棋？11.明明有一个5分硬币，4个2分硬币，8个1分硬币，要组成8分，共有几种不同的搭配方法？12.从小力、小红、小新、小芳4人中挑选2位同学参加小记者选拔比赛，一共有几种不同的选法？3条不同款式的裤子．一件上衣搭配一条裤子，一共有多少种不同的搭配方法？2.小冉有3条不同款式的裙子，5双不同款式的靴子，某日她要去参加聚会，若穿裙子和靴子，则不同的穿着搭配方式的种数为（） A．7 B．8 C．153.用9、0、5三个数字，可以组成多少个不同的三位数？4.课间时间到了，学校为同学们准备的点心有4种：饼干、面包、薯条、蛋挞；准备的饮料有3种：果汁、牛奶、酸奶.每位同学可以任意选择一种点心和一种饮料，请问有几种不同的选择方法？5.红、黄、绿三种颜色可以组成不同的信号方式，有几种不同的信号方式？6.甜甜学数数：1、2、3、4、…一个接一个地往下数，一直数到45，她一共数了（）个含有数字5的自然数．7.用2，3，4三个数字可以组成多少个不同的三位数？写出并从小到大排列．8.从A、B、C、D四位同学中任选2人参加学校演讲比赛，一共有几种不同的可能性？并列举各种可能的结果．参考答案：课堂共同练习：1.4个2.9种3.5种4.13个1，6个25.6次6.12种7.6个8.6种9.4个5,14个210.6盘11.7种12.6种课后自我提升：1.6种2.C3.4个4.12种5.6种6.5个7.一共有6个；从小到大排列为：234＜243＜324＜342＜423＜4328.一共有6种不同的可能性，分别是：AB ，AC ，AD ，BC ，BD ，CD ．1.学习树状加法图：2.标号→画线→数数进行相加3.小猫要回家，它可以有几种不同的走法？4.从甲地到乙地有3条路，从乙地到丙地有4条路，那么从甲地经过乙地到丙地有几种走法？5.一只蜜蜂，从“1”爬到“6”处，有几种不同的走法？6.小蚂蚁从1走到5，不走重复路，有几种不同的走法？7.小明、小红、小强、小莉是好朋友，这天他们每两人互通了一次电话。
第四讲有趣的数阵图经典精讲:数阵图: 将一些数按照一定的要求排列成各种各样的图形。
数阵图是一种趣味性很强的填数游戏, 它的形式多样, 绚丽奇妙。
这里给同学们介绍三种形式的数阵图, 即封闭型数阵图、辐射型数阵图和复合型数阵图。
（一）辐射型数阵图（像雪花）从一个中心出发, 向外作若干条射线, 在每条射线上安放同样多个数, 使其和是一个不变的数。
突破关键：确定中间数, 多算的次数, 公共的和线数x公共的和=数和+中心数x重复次数【例1】把1—5 这五个数分别填在左下图中的方格中, 使得横行三数之和与竖列三数之和都等于9。
【例2】把1—7这七个数分别填入图1中的各○内, 使每条线段上三个○内数的和相等。
【课堂练习】将1～11这11个数分别填入图11中的方格内, 每个数只许用一次, 使相邻两个或三个方格内数的和都相等。
（二）封闭型数阵图（像围墙）多边形的每条边放同样多的数, 使它们的和都等于一个不变的数。
突破关键：确定顶点上的数字, 公共的和边数x公和=数和+重叠数和【例3】把1～6这六个数分别填在下图中三角形三条边的六个○内, 使每条边上三个○内数的和相等。
（本题有24种填法, 你能想出几种？）【例4】将2—9这八个数分别填入右图的○里, 使每条边上的三个数之和都等于18。
【课堂练习】1.1—10这十个数, 分别填在图9中五边形五条边上的十个○内, 并使五条边上的三个○内数的和相等。
2.把1—8这8个数, 填入图13中的八个○内, 使每条线段上的四个数的和, 与每个四边形四个顶点上的四个数的和都相等。
（三）复合型数阵图既有辐射型数阵图的特点, 又有封闭型数阵图的特点。
突破点: 找出关键位置重复次数。
【例5】将1～7这七个数分别填入下图的○里, 使得每条直线上三个数之和与每个圆圈上的三个数之和都相等。
【课堂练习】1.将1.2.3.4.5.6六个数字填入图中的小圆圈内, 使每个大圆上四个数字的和是16。
2. 将1—8这八个数, 分别填入图10中两个圆圈的八个○内, 使每个圆圈上五个○内数的和分别为20、21.22。
小学奥数之数阵图解题方法1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手： 第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．模块一、封闭型数阵图【例 1】 把1～8的数填到下图中，使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯，3年级，第6题 【解析】5-1-3-1.数阵图教学目标知识点拨例题精讲【答案】【例 2】 将1～8这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于14，且数字1出现在四边形的一个顶点上.应如何填？【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便，先在各圆圈内填上字母，如下图（2）.由条件得出以下四个算式：a+b+c=14（1） c+d+e=14 （2） e+f+g=14 （3）a+h+g=14 （4）由（1）+（3），得：a+b+c+e+f+g=28，（a+b+c+d+e+f+g+h ）-（d+h ）=28，d+h=（1+2+3+4+5+6+7+8）-28=8，由（2）+（4），同样可得b+f=8， 又1，2，3，4，5，6，7，8中有1+7=2+6=3+5=8.又1要出现在顶点上，d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性，不妨设b=2，f=6，d=3，h=5. a ，c ，e ，g 可取到1，4，7，8若a=1，则c=14-（1+2）=11，不在1，4，7，8中，不行.若c=1，则a=14-（1+2）=11，不行. 若e=1，则c=14-（1+3）=10，不行. 若g=1，则a=8，c=4，e=7. 说明：例题为封闭型数阵，由它的分析思考过程可以看出，确定各边顶点所应填的数为封闭型数8765432187654321（）（2）h gf ed c ba阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数，使得三条边上的三个数的和都是12，若A 、B 、C 的和为18，则三个顶点上的三个数的和是 。
1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手： 第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．模块一、封闭型数阵图【例 1】 把1～8的数填到下图中，使每个四边形中顶点的数字和相等。
例题精讲知识点拨教学目标5-1-3-1.数阵图【例 2】 将1～8这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于14，且数字1出现在四边形的一个顶点上.应如何填？（1）【例 3】 在如图6所示的○内填入不同的数，使得三条边上的三个数的和都是12，若A 、B 、C的和为18，则三个顶点上的三个数的和是 。
CBA【例 4】 将1至6这六个数字填入图中的六个圆圈中(每个数字只能使用一次)，使每条边上的数字和相等．那么，每条边上的数字和是 ．789fedcba 789【例 5】 将1到8这8个自然数分别填入如图数阵中的8个圆圈，使得数阵中各条直线上的三个数之和都相等，那么A 和B 两个圆圈中所填的数之差(大数减小数)是______．BA【例 6】如图所示，圆圈中分别填人0到9这10个数，且每个正方形顶点上的四个数之和都是18，则中间两个数A与B的和是________。
BA【例 7】把2～11这10个数填到右图的10个方格中，每格内填一个数，要求图中3个22的正方形中的4个数之和相等．那么，这个和数的最小值是多少？11109 8765432【例 8】下图中有五个正方形和12个圆圈，将1~12填入圆圈中，使得每个正方形四角上圆圈中的数字之和都相等．那么这个和是多少?861102912311457【例 9】如图，大、中、小三个正方形组成了8个三角形，现在把2、4、6、8四个数分别填在大正方形的四个顶点；再把2、4、6、8分别填在中正方形的四个顶点上；最后把2、4、6、8分别填在小正方形的四个顶点上．⑴能不能使8个三角形顶点上数字之和都相等？⑵能不能使8个三角形顶点上数字之和各不相同？如果能，请画图填上满足要求的数；如果不能，请说明理由．246824688642【例 10】 将1～16分别填入下图（1）中圆圈内，要求每个扇形上四个数之和及中间正方形的四个数之和都为34，图中已填好八个数，请将其余的数填完.【例 11】 一个3 3的方格表中，除中间一格无棋子外，其余梅格都有4枚一样的棋子，这样每边三个格子中都有12枚棋子，去掉4枚棋子，请你适当调整一下，使每边三格中任有12枚棋子，并且4个角上的棋子数仍然相等（画图表示）。
第十二讲巧填数阵图（一）数学乐园晶晶和莹莹来到了雪精灵国，天空中到处飘着洁白剔透的雪花，就像下面图中的样子.一个雪精灵告诉她们：“你们只要能够把1～7这七个数填在雪花的七个花瓣上，使每三个位于同一直线上的花瓣上的数之和都相等，你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.小朋友们，你喜欢这样的填数字游戏吗？要想准确的填出图中的每一个数，可不是一件容易的事，这就要我们小朋友们认真去观察图，观察数字的排列规律，这样才能找到填图的方法.下面我们就一起来学习吧！基础篇使用数字，，，3，4，5，6，7，8，9做加法.在每一道题中，同一个数字不能重复出现.拓展练习(1)填数，使横行、竖行的三个数相加都得11. (2)填数，使每条线上的三个数之和都得15.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.要使表格中每行、每列和两条对角线上的三个数的和都为18，下面每个方框里应填什么数？拓展练习在下列两图的空格中填上数，使横行和竖行或每条对角线上的三个数相加都等于15.提高篇拓展练习把1，2，3，4，5，7分别填入○里，使每一个大椭圆上的四个数之和等于13.把1，2，3，4，5，6，7这七个数分别填入○里，使每条直线上的三个数相加的和都为12.拓展练习把1～9这九个数字填入下列圆圈内，使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2，3，4，5，6，7，8这七个数分别填入圆圈中，使两个正方形中四个数之和相等19.拓展：如果使两个正方形中四个数之和相等21，又应该怎样填？我会做一做把1，2，3，4，5，6，7这7个数分别填入右图中，使得每条直线上的3个数的和相等.练习十二1.在下面的○里填上适当的数，使每条线上的三个数之和都是12.2.把3～8这6个数，填在下图中使得每行、每列和两条对角线上的三个数的和都为18.6.把数字1，2，3，5，6，7，9填在下面的○里，使每边上的和为15.小朋友，你在少年宫里走过“勇敢者的道路”吗？道路崎岖，充满艰难险阻.但是，它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图，也叫“勇敢者的道路”.图中的道路狭窄、曲折，不易通过，需要小朋友细心和有耐心.现在请小朋友用一枝铅笔，按照图中箭头的方向画出通行路线，而且线条不能碰到两边的“围墙”.小朋友，这可真不容易哦！。
