《控制工程基础》习题答案(燕山大学,第二版)
- 格式:doc
- 大小:4.47 MB
- 文档页数:7

控制工程基础课后习题及答案下面是控制工程基础课后习题及答案的一个示例,供参考。
1.什么是控制工程?答:控制工程是一门研究如何设计、分析和实现控制系统的工程学科。
它涉及到自动控制理论、系统建模、信号处理、电路设计等多个领域。
2.控制系统的基本组成部分有哪些?答:控制系统的基本组成部分包括传感器、执行器、控制器和反馈系统。
传感器用于获取被控对象的状态信息,执行器用于实现控制指令,控制器用于生成控制指令,反馈系统用于将被控对象的输出信息反馈给控制器进行调节。
3.什么是开环控制系统和闭环控制系统?答:开环控制系统是指控制器的输出不受被控对象输出的影响,只根据预先设定的控制指令进行控制。
闭环控制系统是指控制器的输出根据被控对象的输出进行调节,通过反馈系统实现控制。
4.请简述PID控制器的工作原理。
答:PID控制器是一种常用的控制器,其工作原理基于对误差信号进行比例、积分和微分处理。
比例项根据误差的大小产生控制指令,积分项根据误差的累积产生控制指令,微分项根据误差的变化率产生控制指令。
PID控制器的输出是这三个项的加权和。
5.什么是控制系统的稳定性?答:控制系统的稳定性指的是在系统输入变化或外部干扰的情况下,系统输出能够保持在可接受范围内的能力。
稳定的控制系统可以实现良好的跟踪性能和抗干扰能力。
6.如何评价一个控制系统的稳定性?答:一个控制系统的稳定性可以通过判断系统的极点位置来评价。
如果系统的所有极点都位于左半平面,则系统是稳定的;如果系统存在极点位于右半平面,则系统是不稳定的。
7.什么是系统的过渡过程和稳定过程?答:系统的过渡过程指的是系统从初始状态到稳定状态的过程,包括系统的响应时间、超调量等性能指标。
系统的稳定过程指的是系统在达到稳定状态之后的行为,包括稳态误差、稳定精度等性能指标。
8.如何设计一个稳定的控制系统?答:设计一个稳定的控制系统需要满足系统的稳定性条件,例如极点位置的要求。
可以通过选择合适的控制器参数、采用合适的控制策略等方式来实现系统的稳定性。

燕山大学试卷密封线共8 页第 1 页三. 画出图1、2的等效函数方框图,并求出传递函数(10分)。
_F i (s )X o (s )k 21k 1+sfF (s )_1ms 2图1图2 通过调节节流阀使p L =1(t),油缸活塞的直径为d 。
四. 计算题一(10分)K 4s (s +4)_E (s )R (s )C (s )0.2图3某控制系统如图3所示,已知K =125,试求: (1) 系统阶次,类型;(2) 开环传递函数,开环放大倍数; (3) 闭环传递函数,闭环零、极点;(4) 自然振荡频率ωn ,阻尼比ζ,阻尼振荡频率ωd ; (5) 调整时间t s (Δ=2%),最大超调量σp %;(6) 输入信号5)( t r 时,系统的输出终值c (∞)、输出最大值c max ;五. 计算题二(10分)通过过程控制,机器人可以让工具或焊接沿如图4a 所示的预测路线运行。
在图4b 所示的闭环控制系统中,选择最简单的a 、b 、c 的值,使闭环系统沿图4a 所示的运行路线运行时的稳态误差不超过0.05。
100r (t )t10203040R (s )C (s )1s (s +1)(s +2)a bs c /sE (s )_a) b)图4燕山大学试题标准答案院(系): 机械工程学院教研室: 机电控制工程考核课程:控制工程基础07-08 学年季学期开卷涂卡考核专业年级:05机电控制工程1-2班命题教师:高英杰答题教师:高英杰含稳态响应。
3. 什么是相对稳定性?如何描述系统的相对稳定性?相对稳定性是指系统距临界点的稳定性裕度。
一般用相角裕度和幅值裕度来表征。
4. 控制系统综合与校正的实质是什么?在系统校正中,常用的性能指标有哪些?校正的实质就是通过引入校正装置的零、极点,来改变整个系统的零、极点分布,从而改变系统的频率特性或根轨迹的形状,使系统频率特性的低、中、高频段满足希望的性能或使系统的根轨迹穿越希望的闭环主导极点,即使得系统满足希望的动、静态性能指标要求。


科甘£岀J询基班级亦班姓名学号时间燕山大学试卷密封线共8页第1页题号_____________________________________________________ 辿分数一.填空(选择)题(10分,每空0・5分)1.控制论所具有的三个要素有: _________ 、_________ 与_________ O2.反馈控制原理是_____________________ o3.对控制系统的基本要求一般有 _________ 、____________ 、 _________ o4.系统的输出信号对控制作用的影响 _______ =(A)开环有(B)闭环有(C)都没有(D)都有5.一个稳定的系统,在瞬态过程结束后,系统的输出量与__________ 、________ 和 _________ 有关。
6.对数判据是利用__________ 的频率特性来判别_________________ o7.下图所示a, b系统________________ o(A) a稳定、b稳定(B)a稳定、b不稳定(C) a不稳定、b稳定(D) a不稳定、b不稳定&若保持如不变而增大:值,贝!1会使二阶振荡系统的超调量恪________________ 。
9.一阶惯性系统的调整时间与________________ 有关。
10.若系统传递函数的极点和零点都位于s平面的左半部,这种系统称为_______________ o反之, 若系统的传递函数具有位于s平面右半部的极点或零点,则系统称为 ________________ 。
11.自动控制是在没有人直接参与的情况下利用_____________ 使被控对象在一定精度范围内按照___________ 变化。
二.简答题(10分,每题2分)1.动力学系统的数学模型主要包括哪些种类?获取系统的数学模型有哪些方法?2.频率特性的物理意义,频率特性与频率响应有何区别?频率响应是否只包含稳态响应?3.什么是相对稳定性?如何描述系统的相对稳定性?4.控制系统综合与校正的实质是什么?在系统校正中,常用的性能指标有哪些?5.控制系统的时域分析和频域分析各有什么特点?它们之间的联系与区别是什么?燕山大学试卷三. 画出图1. 2的等效函数方框图,并求出传递函数(10分)。




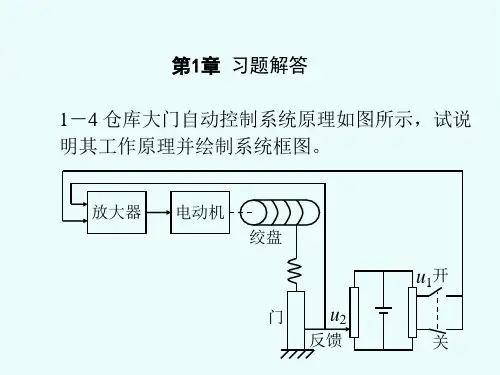
第一章习题解笞U]>U2 U\ U2第二章习题解答2-1a) b)d)f)L^f| 忙d)f\ — fl =^2X O严(f)=$(M+E ⑴虑 如(f) =iQ)RRC^-u o (t)^u o (t) = RC^-u^t) at at fs (r)=B 低[xi (f) -曲(幼 j/B (t)=fK (t) = KXo(t) B dB d 『八10602斤不%()+%©二斤击可()占dR^c —% (0+ (*i + 心)% ⑴=邛应 ~u i (0+ R 2u t (0 atati =i R +,C u o =IR?:R R 严冃3宙 % =gR\ +u oa)=K ](旳一兀)+」:dx o ](J?l + J?2)C —«c (!)+ %("■ R Q C — Wj(O + tti (Oat at(K[ + K2)B — x o (t)+ K\K2X o (t)= K\R 〒曲(f)+ 琦心再(f)dt at10602a) b) c) Q © f)U Q —1/?2 + — j icit— Z/?| + iR-f H —J idte)dxK\% K i (兀 _ %) = K 》(兀)—x)=号二dtoB 2+ (®K° ++ B'B? + 场*3 + 水2〃?)& 2+ (K }B 2+K }B 3 + 心汝 + KM 巴2 + K }K 2X 2 dt3J S + 2用 + 8S-丘($ + 2)($戈+2$十4)广、■炉+ 5,2+9用+7E ($+恥 + 2)乡一rn\fU2K 2rdx { dx 2< dt dt ;/(O™-坷罕~_叭 dtdxj … 一 —- - K?x^ = m dtdx l dx 2dt dt护d 2x 2 2~d^ k,用典2+ (的+创坷+用2创+加2*3);?7皿乔对)13173 G($)= --------------- —(£+。
控制工程基础习题解答第二章2-1.试求下列函数的拉氏变换,假定当t<0时,f(t)=0。
(1).()()t t f 3cos 15-= 解:()[]()[]9553cos 152+-=-=s ss t L t f L (2). ()t et f t10cos 5.0-=解:()[][]()1005.05.010cos 25.0+++==-s s t eL t f L t(3). ()⎪⎭⎫⎝⎛+=35sin πt t f 解:()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s st t L t L t f L π 2-2.试求下列函数的拉氏反变换。
(1).()()11+=s s s F解:()[]()⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+=---11121111s k s k L s s L s F L()10111==⎥⎦⎤⎢⎣⎡+=s s s s k()()111112-=-=+⎥⎦⎤⎢⎣⎡+=s s s s k ()[]te s s L s F L ----=⎥⎦⎤⎢⎣⎡+-=111111 (2).()()()321+++=s s s s F解:()[]()()⎥⎦⎤⎢⎣⎡+++=⎥⎦⎤⎢⎣⎡+++=---3232121111s k s k L s s s L s F L()()()1223211-=-=+⎥⎦⎤⎢⎣⎡+++=s s s s s k ()()()2333212=-=+⎥⎦⎤⎢⎣⎡+++=s s s s s k ()[]tt e e s s L s F L 231123221-----=⎥⎦⎤⎢⎣⎡+++-= (3).()()()2222522+++++=s s s s s s F解:()[]()()⎥⎦⎤⎢⎣⎡+++++=⎥⎦⎤⎢⎣⎡+++++=---22222225232112211s s k s k s k L s s s s s L s F L()()()22222225221-=-=+⎥⎦⎤⎢⎣⎡+++++=s s s s s s s k ()()()3331331222222513223222232==-=---=-+---=++⎥⎦⎤⎢⎣⎡+++++=--=+k k jjjjk k k j s s s s s s s s j s k s k ()[]()()t e e s s s L s s s s L s F L tt cos 32111322223322221211-----+-=⎥⎦⎤⎢⎣⎡+++++-=⎥⎦⎤⎢⎣⎡+++++-=2-3.用拉氏变换法解下列微分方程(1)()()()()t t x dt t dx dtt x d 18622=++,其中()()00,10===t dt t dx x 解:对方程两边求拉氏变换,得:()()()()()()()()()()()()()()()()()[]()0,8747818747814242168616181618060042132132122222≥-+==-===++++=++++=++++==+-+-=+-+=-----t e e s X L t x k k k s k s k s k s s s s s s s s s s s X ss X s sX s s X s ss X x s sX t dt t dx sx s X s t t(2)()()210=+t x dtt dx ,其中()00=x 解:对方程两边求拉氏变换,得:()()()()()()()()()[]()0,515151511010221021001012121≥-==-==++=+==+=+---t e s X L t x k k s k s k s s s X s s X s sX ss X x s sX t(3)()()300100=+t x dtt dx ,其中()500=x 解:对方程两边求拉氏变换,得:()()()()()()()()()[]()0,4734731001003005030010050300100010012121≥+====++=++==+-=+---t e s X L t x k k s k s k s s s s X ss X s sX s s X x s sX t2-4.某系统微分方程为()()()()t x dtt dx t y dt t dy i i 322300+=+,已知()()0000==--i x y ,其极点和零点各是多少?解:对方程两边求拉氏变换,得:()()()()()()()()()()()233223323022030000-=-=++==+-=+-z p i i i i s s s s s X s Y s G s X x s sX s Y y s sY2-5.试求图2-25所示无源网络传递函数。
控制工程基础习题解答
第一章
1-1.控制论的中心思想是什么?简述其发展过程。
维纳(N.Wiener)在“控制论——关于在动物和机器中控制和通讯的科学”中提出了控制论所具有的信息、反馈与控制三个要素,这就是控制论的中心思想
控制论的发展经历了控制论的起步、经典控制理论发展和成熟、现代控制理论的发展、大系统理论和智能控制理论的发展等阶段。
具体表现为:
1.1765年瓦特(Jams Watt)发明了蒸汽机,1788年发明了蒸汽机离心式飞球调速器,2.1868年麦克斯威尔(J.C.Maxwell)发表“论调速器”文章;从理论上加以提高,并首先提出了“反馈控制”的概念;
3.劳斯(E.J.Routh)等提出了有关线性系统稳定性的判据
4.20世纪30年代奈奎斯特(H.Nyquist)的稳定性判据,伯德(H.W.Bode)的负反馈放大器;
5.二次世界大仗期间不断改进的飞机、火炮及雷达等,工业生产自动化程度也得到提高;
6.1948年维纳(N.Wiener)通过研究火炮自动控制系统,发表了著名的“控制论—关于在动物和机器中控制和通讯的科学”一文,奠定了控制论这门学科的基础,提出
了控制论所具有的信息、反馈与控制三要素;
7.1954年钱学森发表“工程控制论”
8.50年代末开始由于技术的进步和发展需要,并随着计算机技术的快速发展,使得现代控制理论发展很快,并逐渐形成了一些体系和新的分支。
9.当前现代控制理论正向智能化方向发展,同时正向非工程领域扩展(如生物系统、医学系统、经济系统、社会系统等),
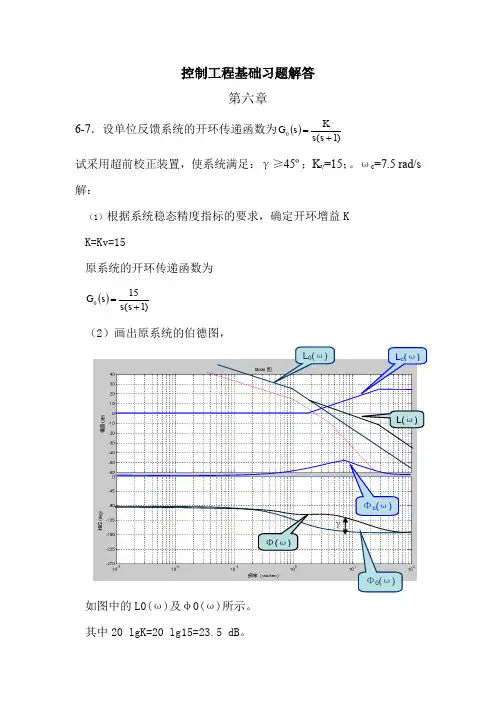
1-2.试述控制系统的工作原理。
控制系统就是使系统中的某些参量能按照要求保持恒定或按一定规律变化。
它可分为人工控制系统(一般为开环控制系统)和自动控制系统(反馈控制系统)。
人工控制系统就是由人来对参量进行控制和调整的系统。
自动控制系统就是能根据要求自动控制和调整参量的系统,系统在受到干扰时还能自动保持正确的输出。
它们的基本工作原理就是测量输出、求出偏差、再用偏差去纠正偏差。
1-3.何谓开环控制与闭环控制?
开环控制:系统的输出端和输入端之间不存在反馈回路,输出量对系统的控制作用没有影响。
系统特点:系统简单,容易建造、一般不存在稳定性问题,精度低、抗干扰能力差。
闭环控制:系统的输出端和输入端存在反馈回路,输出量对控制作用有直接影响。
闭环的反馈有正反馈和负反馈两种,一般自动控制系统均采用负反馈系统,闭环控制系统的特点:精度高、抗干扰能力强、系统复杂,容易引起振荡。
1-4.试述反馈控制系统的基本组成。
反馈控制系统一般由以下的全部或部分组成(如图示):
1.给定元件:主要用于产生给定信号或输入信号
第三章
3-1.已知二阶系统的闭环传递函数为()()2
2
2
2n
n n s s s R s C ωςωω++=,其中ζ=0.6,ωn =5rad/s ,试求在单位阶跃输入下的瞬态响应指标t r 、t p 、σp %、和t s 。
解:
s
rad rad
n d /46.0151927.013.536
.06.01tan
1tan
222
1
2
1
=-=-==︒=-=-=--ςωως
ςβ 0.55(s)4927
.0=-=-=
πωβπd r t ()s t d p 79.04
===
π
ωπ %5.9%2
2
6.016.01===--
--
πς
ςπ
σe e
p
()()s t s t n
s n
s 33.15
6.04
4
156.03
3
=⨯=
=
=⨯==ςωςω
3-2.已知某系统的框图如图3-16所示,要求系统的性能指标为σ
p
%=20%,t p =1s ,试确定系统的K 值和A 值,并计算t r 和t s 之值。
解:
()()K
AK K K
s AK s K
s n 2112
+=
=+++=ςωφ
45
.02.0%2
1===--
ςσςςπ
e p
第二章
2-1.试求下列函数的拉氏变换,假定当t<0时,f(t)=0。
(1).()()t t f 3cos 15-= 解:()[]()[]9
553cos 152
+-=-=s s
s t L t f L (2). ()t e t f t 10cos 5.0-= 解:()[][]
()100
5.05
.010cos 2
5.0+++=
=-s s t e L t f L t (3). ()⎪⎭
⎫
⎝
⎛+
=35sin πt t f 解:()[]()
252355cos 235sin 2135sin 2
++=⎥⎦
⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s s
t t L t L t f L π 2-2.试求下列函数的拉氏反变换。
(1).()()
11+=
s s s F
解:()[]()⎥⎦⎤⎢⎣⎡++=⎥⎦
⎤⎢
⎣⎡+=---11121
111
s k s k L s s L s F L
()10111==⎥
⎦⎤
⎢⎣⎡+=s s s s k ()()111112-=-=+⎥⎦
⎤⎢⎣⎡+=s s s s k
()[]t
e s s L s F L ----=⎥⎦
⎤⎢⎣⎡+-=111111 (2).()()()
321
+++=
s s s s F
解:()[]()()⎥
⎦⎤⎢⎣⎡+++=⎥⎦
⎤⎢
⎣⎡+++=---3232121
111
s k s k L s s s L s F L
第四章
4-1.试求下列函数的幅频特性A (ω)、相频特性Φ(ω)、实频特性U (ω)和虚频特性V (ω)。
(1). ()1
305
1+=
ωωj j G
(2).
()()11.01
2+=
ωωωj j j G
解:
(1). ()1
9001501
9005
2
21+-+=
ωω
ωωj
j G ()1
90052
+=
ωωA
()()ωωφ30arctan
-= ()19005
2
+=
ωωU
()1
9001502+-=ωω
ωV
(2). ()(
)()
1
01.01
101.01.02
22+-+-
=ωωωωj j G ()1
01.01
2
+=
ωωωA
()ω
ωφ1.01
arctan
= ()(
)
1
01.01
.02+-
=ωωU
()()
1
01.01
2+-=ωωωj
V
4-2.某系统传递函数()1
25.05
+=s j G ω,当输入为()
304cos 5-t 时,试求
系统的稳态输出。
控制工程基础习题解答
第五章
5-1.已知开环系统的传递函数如下,试用罗斯-赫尔维茨判据判别其闭环稳定性。
(1). ()()()()()32110+++=
s s s s s H s G (2). ()()()()()()38.05.022.0++++=
s s s s s s H s G (3). ()()()
50
600300100
2
2++=
s s s s H s G (4).
()()()
24
81
322+++=
s s s s s H s G
解:
(1). 特征方程为01016523
=+++s s s
10
141051610123s s s s
第一列全部大于零,所以闭环稳定。
(2). 特征方程为04.04.13.43.42
3
4
=++++s s s s
4
.097.04.097.34.13.44.03.41
01234s s s s s 第一列全部大于零,所以闭环稳定。
(3). 特征方程为0100506003002
3
4
=+++s s s
控制工程基础习题解答
第六章
6-1.已知单位反馈系统的开环传递函数为()()()
16.013.0++=s s s K
s G 。
试求:
(1). 静态误差系数K p 、K v 、K a 。
(2). 系统对阶跃输入的稳态误差。
(3). 系统对输入为r(t)=2t 时的稳态误差。
解:稳定性验算:
特征方程:09.018.023=+++K s s s
K K
K
s s s s 2.019.01
18.00
123-
当50<<K 时,系统稳定,求解误差有意义。
(1). Ⅰ型系统。
K p =∝ K v =K K a =0
(2). 011
=+=
p
ssp K e
(3). 输入为r(t)=2t 时,。