解决问题的策略练习题(三)画图要点

（苏教版）四年级数学下册《解决问题的策略》练习题四年级应⽤题练习（⼀）⼀、画图整理，再解答1. ⼩红和⼩明同时从甲⼄两地沿⼀条公路相对⾛来。

⼩红每分钟⾛65⽶，⼩明每分钟⾛60⽶，经过5分钟两⼈相遇。

两地相距多少⽶？2. ⼩花和⼩迎同时从同⼀地点出发，⼩华向南⾛，每分⾛55⽶；⼩迎向北⾛，每分⾛45⽶。

经过5分钟，两⼈相距多少⽶？3. 我们学校原来有⼀个长⽅形操场，长60⽶，宽40⽶。

扩建校园时，操场的长增加了20⽶，宽增加了10⽶。

操场的⾯积增加了多少平⽅⽶？4. ⼀个正⽅形花坛长5⽶，四周有⼀条1⽶宽的⼩路。

求⼩路的⾯积。

5. 学校有⼀块长⽅形试验⽥。

如果这块试验⽥的长增加5⽶或8⽶，⾯积都⽐原来增加40平⽅⽶。

你知道原来试验⽥的⾯积是多少平⽅⽶吗？⼆、列表整理，再解答1. ⼩明家种了696棵桃树和苹果树，15⾏桃树和18⾏苹果树。

桃树每⾏20棵，苹果树每⾏多少棵？2. 公路队修⼀条长1200⽶的路，第⼀周修了5天，平均每天修128⽶。

第⼆周准备每天修140⽶，还要修多少天？三、解决问题1. ⼀列货车和⼀列客车同时在早晨6时从甲地开往⼄地，货车平均每⼩时⾏45千⽶，客车平均每⼩时⾏60千⽶，早晨8时，客车⽐货车多⾏多少千⽶？2.唐⽼鸭和⽶⽼⿏在环形跑道上跑步，两⼈从同⼀地点同时出发，唐⽼鸭每秒跑3⽶，⽶⽼⿏每秒跑4⽶，反向⽽⾏，45秒两⼈相遇。

（1）环形跑道长多少⽶？（2）如果同向⽽⾏，多少秒后⽶⽼⿏和唐⽼鸭再次相遇？3.甲、⼄⼆⼈分别从两地同时出发相向⽽⾏，甲每⼩时⾛6千⽶，⼄每⼩时⾛4千⽶，2⼩时后还相距4千⽶。

两地相距多少千⽶？4.东升村请甲⼄两个筑路队来维修地下⽔渠，甲队每天修150⽶，⼄队每天修200⽶，他们分别从阳光路两端同时修起，5天在中⼼花园相遇。

（1）阳光路⽔渠长多少⽶？（2）接着他们同时从中⼼花园出发，分别维修亚光路和友谊路的地下⽔渠。

甲队⽤4天时间维修了亚光路，⼄队⽤6天时间维修了友谊路。

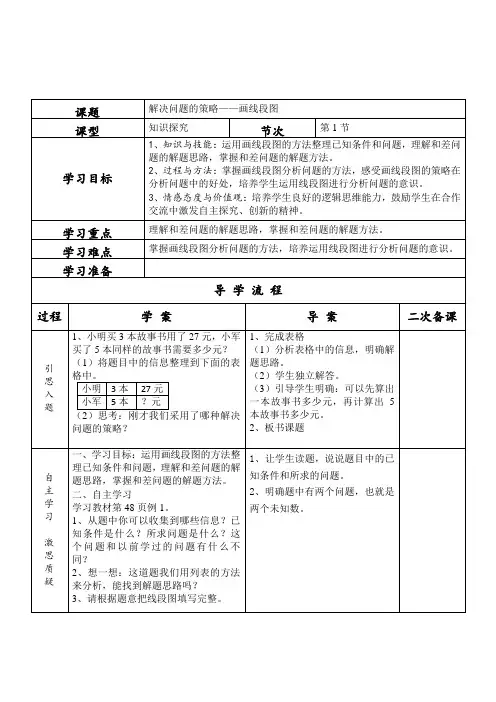
课题 课型解决问题的策略——画线段图 知识探究节次第1节学习目标1、知识与技能：运用画线段图的方法整理已知条件和问题，理解和差问 题的解题思路，掌握和差问题的解题方法。

2、过程与方法：掌握画线段图分析问题的方法，感受画线段图的策略在 分析问题中的好处，培养学生运用线段图进行分析问题的意识。

3、情感态度与价值观：培养学生良好的逻辑思维能力，鼓励学生在合作 交流中激发自主探究、创新的精神。

理解和差问题的解题思路，掌握和差问题的解题方法。

掌握画线段图分析问题的方法，培养运用线段图进行分析问题的意识。

学习重点 学习难点 学习准备导 学 流 程 过程 学 案1、小明买 3 本故事书用了 27 元，小军 买了 5 本同样的故事书需要多少元？ （1）将题目中的信息整理到下面的表 格中。

小明 3 本 27 元 小军 5 本 ？元 （2）思考：刚才我们采用了哪种解决 问题的策略？ 一、学习目标：运用画线段图的方法整 理已知条件和问题，理解和差问题的解 题思路，掌握和差问题的解题方法。

二、自主学习 学习教材第 48 页例 1。

1、从题中你可以收集到哪些信息？已 知条件是什么？所求问题是什么？这 个问题和以前学过的问题有什么不 同？ 2、想一想：这道题我们用列表的方法 来分析，能找到解题思路吗？ 3、请根据题意把线段图填写完整。

导 案1、完成表格 （1）分析表格中的信息，明确解 题思路。

（2）学生独立解答。

（3）引导学生明确：可以先算出 一本故事书多少元，再计算出 5 本故事书多少元。

2、板书课题 1、让学生读题，说说题目中的已 知条件和所求的问题。

2、明确题中有两个问题，也就是 两个未知数。

二次备课引 思 入 题自 主 学 习 激 思 质 疑一、小组汇报 二、全班交流 1、观察线 段图 ，想一 想 可以先 算什 么？ 2、列式解答： 合 作 交 流 集 思 释 疑1、交流解题策略。

学生交流得出：由于两人的邮票 数量都是未知的，用列表的方法 进行分析，不容易找到解题思路。

第三单元解决问题的策略复习1、两步计算解决实际问题：解决问题可以从问题出发，根据问题分析数量关系，确定先算出什么是关键。

2、画图解决问题：学会根据题中的信息与问题画出线段图，分析数量关系，确定先算什么。

所列出的每一个算式要充分理解所表示的意义。

一.把条件补充完整，并写出数量关系式（1），已经看了13天，每天看20页。

还剩多少页没有看？=还剩的页数（2），红彩带的长度是蓝彩带的4倍。

红彩带比蓝彩带长多少米？=红彩带比蓝彩带长的米数二、先想一想每一步可以怎样算，再列式计算1.商店里有45筐苹果，20筐梨。

香蕉的筐数比苹果和梨的总筐数少4筐。

香蕉有多少筐？（1）列式：2.学校买了62瓶红墨水，买的黑墨水比红墨水少3瓶，买的蓝墨水瓶数是黑墨水的2倍，买的蓝墨水有多少瓶？(1)列式：（2）列式：3.动物园有15只孔雀，鹦鹉的只数是孔雀的3倍（1）鹦鹉比孔雀多多少只？①列式：②列式：（2）鹦鹉和孔雀一共有多少只？①列式：②列式：三、根据问题分析数量关系，再解答1.学校食堂每天吃掉大米130千克，一周后（其中两天休息）仓库还剩320千克。

仓库内原来有多少千克大米？2.红气球有23个，黄气球的个数是红气球的3倍。

红气球和黄气球一共有多少个？3.三年级同学做花送给幼儿园的小朋友。

同学们做了红花45朵，做的黄花比红花少18朵。

两种花一共做了多少朵？4、育才小学开展“献爱心”捐款活动，三年级捐款356元，四年级捐款数是三年级的2倍。

三、四年级一共捐款多少元？（先画线段图，再解答）5、欣欣收集了15枚邮票，天天收集的邮票枚数是欣欣的2倍。

欣欣和天天一共收集了多少枚邮票？（先画线段图，再解答）四、看图列式计算1、2、3、4、5、6、7、。

1、四（一）班一共有学生48人，其中男生比女生多4人，四（一）班男生和女生各有多少人？2、在一张长20厘米、宽15厘米的长方形纸上剪去一个最大的正方形，剩余部分的面积是多少？（先在图上画一画，再解答）3、在一个边长是8米的正方形草坪四周有一条1米宽的花圃。

在花圃里栽有牡丹花，每棵占地1平方米，一共要栽多少棵？（先画出示意图，再解答）4、甲仓库存粮是乙仓库的5倍。

如果从甲仓库运12吨去乙仓库，两个仓库的存粮数就一样多。

原来甲、乙两个仓库各存粮多少吨？（先画图整理，再解答）5、两筐水果共重150千克，第一筐比第二筐少10千克，两筐水果各多少千克？6、甲、乙两人同时以相同的速度打字，2分钟共打了240个字，已知甲每分钟比乙多打10个字，甲、乙两人每分钟各打多少个字？7、A、B两校共有学生864人，为了照顾学生就近入学，从A校调入B校32人，这样A校学生还比B 校多48人，A、B两校原来各有学生多少人？8、波波有圆珠笔30支，亮亮有圆珠笔15支，问亮亮给波波多少支后，波波的圆珠笔支数是亮亮的8倍？9、苹果和梨共40千克，苹果比梨多2袋，苹果和梨每袋都重5千克，问苹果和梨各多少千克？10、长方形操场的长与宽相差80米，沿操场跑一周是400米，求这个操场的长与宽是多少米？11、一个长方形的周长是86米，长比宽多3米。

这个长方形的面积是多少平方米？12、一个长方形操场，长70米，宽40米。

扩建时，操场的长增加了40米，宽增加到60米。

操场的面积比原来增加了多少平方米？13、一个正方形花圃，边长是18米，四周有一条2米的小路。

小路的面积是多少平方米？14、我们学校原来有一个长方形操场，长60米，宽40米。

扩建校园时，操场的长增加了20米，宽增加了10米。

操场的面积增加了多少平方米？15、一个正方形花坛长5米，四周有一条1米宽的小路。

求小路的面积。

16、学校有一块长方形试验田。

如果这块试验田的长增加5米或宽增加8米，面积都比原来增加40平方米。

小学数学 解决问题的策略——画图法知识梳理星河小学美术组男生人数占总人数的，已知女生有21人，男生有多少人？小明的办法：画图法： 男生占52女生21人？人通过画图，可以看出男生人数有2份，女生人数有3份。

先求出1份是多少，再求这样的两份是多少。

列式为：21÷3×2＝14（人）小红的办法：把“男生人数占总人数的52”转化成男、女生人数的比是2:(5－2)＝2:3，即男生人数是女生的32，已知“女生有21人”，利用分数乘法计算。

列式为：21×32＝14（人）我的办法：已知“男生人数占总人数的”说明女生人数占总人数的1－＝，根据“女生有21人”，可以求出总人数，再用总人数减去女生人数即可。

列式为：21÷（1－）＝35（人），35－21＝14（人） 答：美术组有男生14人。

解决问题的策略1. 选择画图法的策略能使数量关系更直观、更清楚；2. 把分数转化成比，更容易理解数量之间的关系；3. 求已知数量占单位“1”的分量，求出单位“1”，再求未知数量。

例题1 赵大娘家养的公鸡与母鸡的只数比是4:7，公鸡比母鸡少30只。

赵大娘家养的公鸡有多少只？解答过程：画线段图解决问题，公鸡与母鸡的只数比是4:7，则公鸡有4份，母鸡有7份，公鸡比母鸡少3份，已知公鸡比母鸡少30只，先求出1份是多少，再求这样的4份是多少。

答案：7－4＝3，30÷3＝10（只），4×10＝40（只）答：赵大娘家养的公鸡有40只。

例题2 先根据题意把线段图补充完整，再解答。

（1）一辆汽车从甲地开往乙地，已经行驶了全程的30％，离乙地还有140千米。

这辆汽车行驶了多少千米？（2）六年级生物小组养的白兔和黑兔的只数比是5:3，白兔比黑兔多12只，白兔和黑兔一共有多少只？解答过程：（1）已经行驶了全程的30％，还有全程的70％没有行驶，已知离乙地还有140千米，即全程的70％正好是140千米。

一、画线段图1、小明和小红共有72朵玫瑰，小红比小明多12朵。

两人各有玫瑰多少朵？2、学校有足球和篮球共56个，篮球比足球少14个，两种球各有多少个？3、小华和小芳参加集邮，小华收集的邮票数是小芳的3倍，两人共有邮票96枚。

小华和小芳各有邮票多少枚？4、小强和小华购买同样的计算器，小强买了3个，小华买了5个，小强比小华少花30元。

计算器的单价是多少元/个？5、小明身上的钱是小华5倍，小明如果给小华40元，那么两人的钱就一样多。

小明和小华原来各有多少元？6、张宁和王晓星一共有86元钱。

王晓星给张宁8元后，两人的钱同样多。

两人原来各有多少元钱？7、一个双层书架，上层书的本数是下层的5倍。

如果从上层搬60本到下层，那么两层书的本数正好相等。

原来上、下层各有图书多少本？8、甲乙两地相距850千米，一辆汽车从甲地开往乙地，已经行了5小时，剩下的路程比已经行的少50千米。

这辆汽车的平均速度是多少千米/时？9、李娟在综合课上把70厘米的花边剪成了4条同样长的短花边和1条长花边，如果长花边比短花边长20厘米，每条短花边是多少厘米？长花边呢？10、小明和小红有同样多的课外书，从小明的书出拿走35本，从小红的书中拿走72本后，小明余下的书是小红余下的2倍。

小明和小红原有图书都是多少本？二、面积画图1、一个边长为25米的长方形的绿地，如果把它的长增加15米，它的面积就增加360平方米，求现在这块绿地的面积是多少平方米？2、把一个正方形的操场的一组对边各增加18米，这样操场的面积就增加了900平方米，原来操场的面积是多少平方米？3、一个长方形的菜地，种番茄的面积比菜园面积的一半少了8平方米，其余的22平方米种黄瓜，这个菜园的面积是多少平方米？4、张叔叔家有一块长方形菜地，如果长增加5米，面积就增加50平方米；如果宽增加3米，面积就增加60平方米。

这块菜地的面积是多少平方米？5、在一张长20厘米、宽15厘米的长方形纸上剪去一个最大的正方形，剩余部分的面积是多少？（先在图上画一画，再解答）三、行程画图1、小强和小明家相距2400米，两人同时从家中出发相向而行，小强每分钟走50米，小明每分钟走70米，他们经过多长时间相遇？（先画图整理，再解答）2、一辆公共汽车和一辆小轿车同时从相距480千米的两地相向而行，公共汽车每小时行40千米，小轿车每小时行50千米，5小时后两车还相距多少千米？3、甲乙两人同时从两地骑车相向而行，甲每小时行驶20千米，乙每小时行驶18千米，两人相遇时距离全程中点3千米，求全程长多少千米？。

《解决问题的策略（画示意图）》一、教学目标1.使学生加深认识画图的策略,学会画示意图整理实际问题的条件和问题,能利用示意图分析数量关系,说明解决实际问题的思路，正确列式解答。

2.使学生经历画示意图分析数量关系、解决实际问题的过程,进一步感受画图策略对于解决问题的价值,培养几何直观和分析、推理等思维能力，提高分析问题、解决问题的能力。

3.使学生获得通过画图成功解决实际问题的体验,感受数学方法的力量,进一步积累解决实际问题的经验,增强解决问题的策略意识，提高学好数学的信心。

二、教学重点难点【教学重点】掌握画示意图分析、解决问题的策略。

【教学难点】掌握正确画示意图的方法。

三、教学准备课件四、教学过程一、知识回顾,引入新课老师通过几个题目来帮助学生，回顾之前所学习的用画线段图的策略来解决问题的知识，帮助学生扎实基础。

同时，也为本节课的新课做一个引入。

师：同学们，在这之前，我们已经学会了用画线段图的策略来解决我们的实际问题，那么在上新课之前，老师想要通过这样的两道题目来检测大家对于这部分内容的熟悉程度，首先我们来看这样的判断。

生：读题判断。

老师结合学生的答题情况进行辅助教学。

师：看来我们绝大部分小朋友都能正确的使用线段图来表示我们题目的含义，接下来让我们再来看这样的题目。

生：读题分析师：请学生进行讲解，出示答案。

通过简单的练习，帮助学生回顾上节课的内容。

接着老师出示一个长方形，要求学生能够通过自己的方法来扩大长方形的面积和缩小长方形的面积，引入本节课的内容。

师：同学们，仔细观察，这是一个什么图形呢？生：长方形。

师：对，这是一个长方形，如果我想将这个长方形的面积扩大成为另外一个长方形，你会怎么做？先同桌之间互相说一说。

生：同坐交流。

师：组织学生交流，并分享。

师：老师通过大家的回答，画出了这样的几幅图，你还能对照着说一说，它的方法吗？（出示图形）结论：可以通过增加长、增加宽或者同时增加长和宽。

师：如果我想将这个长方形的面积缩小成为另外一个长方形，你是否也能对照面积扩大的方法画出对应的图形？生：交流总结。

解决问题的策略画图教学目标：1. 理解画图作为一种解决问题的策略。

2. 学会使用画图来分析和解决数学问题。

3. 培养学生的逻辑思维能力和创造力。

教学内容：一、画图策略的引入1. 引入话题：讨论解决问题时遇到困难的情况，引导学生思考如何更好地解决问题。

2. 举例说明：给出一个简单的数学问题，如2x + 3 = 7，让学生尝试用画图的方法来解决。

二、画图解决问题的步骤1. 步骤一：明确问题：读懂问题的意思，找出关键信息。

2. 步骤二：选择合适的图形：根据问题的特点，选择合适的图形来表示问题。

3. 步骤三：画出图形：根据选择的图形，仔细画出图形，尽量准确。

4. 步骤四：分析图形：观察图形，找出图形的特征和关系。

5. 步骤五：得出结论：根据图形的分析，得出问题的解答。

三、画图策略的实践1. 小组讨论：学生分组，每组选择一个数学问题，用画图的方法来解决。

2. 分享结果：每组展示他们的画图过程和最终答案，讨论不同组之间的差异和优劣。

四、画图策略的拓展1. 引入不同类型的图形：除了简单的直线和曲线，还可以使用多边形、圆等更复杂的图形来解决问题。

2. 引入数学符号：在画图中引入数学符号，如加号、减号、等于号等，使图形更加准确和清晰。

2. 教师反思：教师引导学生思考画图策略的局限性和适用范围，以及如何与其他策略结合使用。

教学资源：1. 纸张、铅笔、直尺等绘图工具。

2. 数学问题示例和案例。

教学评价：1. 学生参与度：观察学生在课堂上的积极参与和合作情况。

2. 学生解答：评估学生用画图策略解决问题的准确性和创造性。

3. 学生反馈：收集学生的反馈意见，了解他们对画图策略的理解和应用情况。

六、画图策略在不同学科的应用1. 数学问题：引入其他数学领域的问题，如几何图形的面积、体积计算，用画图策略来帮助解决问题。

2. 科学问题：举例说明如何在科学领域中使用画图策略，如绘制温度随时间变化的图表，帮助分析数据。

七、画图策略的数字化工具1. 介绍软件：介绍一些常用的数字化绘图工具，如GeoGebra、Desmos等，让学生了解并尝试使用这些工具来解决问题。

通过上面的线段图可知：
①男生人数是女生的23
，男生和女生一共有5份，可以说男生人数是美术组总人数的25
； ②也可以把男生人数和女生人数转化成比的形式，即男、女生人数的比是2:3。

3．利用转化法解题
(1)解题思路。

男、女生人数的比是2:3，即男生人数是美术组总人数的25
，总人数已知，根据比的知识用乘法求出男、女生人数。

(2)正确解答。

35×25
＝14(人) 35－14＝21（人） 答：美术组的男生有14人，女生有21人。

4．利用方程法解题
(1)解题思路。

“男生人数是女生的23
”，男生人数和女生人数相比，女生人数是单位“1”。

男生人数和女生人数都是未知的，可设单位“1”（女生人数）为x ，男生人数可用含有x 的式子表示出来。

根据等量关系“男生人数＋女生人数＝美术组总人数”列方程。

(2)正确解答。

解：设女生有x 人。

23
x ＋x ＝35。

解决问题的策略---画图法
1、一二三班共有153人，一班比二班多2人，三班比二班多1人，求每班各有几人？
2、有99千克梨，分给甲、乙、丙三个组，甲组比乙组多分4千克，乙组比丙组多分4千克，三个组各得多少千克？
3、一部书有上、中、下三册，上册比中册贵1元，中册比下册贵2元，这部书售价32元，上、中、下三册各多少元？
4、哥哥和弟弟共有画片38张，弟弟给哥哥3张后还比哥哥多2张，哥哥和弟弟原来各有画片多少张？
5、把100米长的绳子剪成三段，第二段比第一段多16米，第三段比第一段少18米，三段绳子各长多少米？
6、小华和爷爷今年共72岁，爷爷的岁数是小华的7倍，爷爷比小华大多少岁？
7、光明小学有学生760人，其中男生比女生
的3倍少40人，男女生各有多少人？8、师徒两人共加工105个零件，师傅加工的
个数比徒弟的3倍还多5个，师傅和徒弟各加工零件多少个？
9、甲、乙两仓库共存粮264吨，甲仓库存粮是乙仓库存粮的10倍。

甲、乙两仓库各存粮多少吨？
10、甲、乙两人共有150张画片，甲的张数比乙的2倍多30张，两人各有几张画片？
11、哥哥和弟弟共有图书120本，哥哥的图书是弟弟的3倍，哥哥有图书多少本？
12、已知大、小数之差是152，大数是小数的5倍。

求大、小两数各是多少？13、甲存款数是乙的4倍，甲比乙多存600元。

甲、乙两人各存款多少元？
14、徒弟比师傅少加工105个零件，师傅加工的个数比徒弟的3倍还多5个，师傅和徒弟各加工零件多少个？
15、李爷爷家养的鸭比鹅多118只，鸭的只数是鹅的3倍，请问鸭和鹅各有多少只？16、两个书架，甲书架存书相当于乙书架存
书量的3倍多15本，甲书架比乙书架存书多135本，则甲书架存书多少本？。

解决问题的策略——画图法
一、说教材
《解决问题的策略——画图法》是苏教版四年级下册第四单元的内容。

本课是在学生已经学习了长方形、正方形的面积计算的基础上，教学用“画图”的策略解决相关实际问题。

[教学目标]
本课的教学目标是：
（1）使学生学会用画直观示意图的方法整理有关信息，分析实际问题中的数量关系，确定解决实际问题的正确思路。

（2）使学生在对解决实际问题过程的不断反思中，感受画图法在解决问题中的价值，体会到画图整理信息是解决问题的一种常用策略。

（3）使学生进一步积累解决实际问题的经验，增强解决问题的策略意识，获得解决问题的成功体验，提高学好数学的信心。

[重难点]
教学重点：体验策略的价值，会根据题意画出示意图。

教学难点：借助画图的策略解决面积计算的实际问题。

二、说教法学法
依据《数学课程标准》中“变注重知识获得的结果为知识获得的过程”的教育理念，我以学生发展为立足点，以自主探索为主线，以求异创新为宗旨，采用多媒体辅助教学，运用设疑激趣、直观演示、实际操作等教学方法，引导学生动手操作、观察辨析、自主探究，让学生全面、全程地参与到每个教学环节中，充分调动学生学习的积极性，培养学生的自主学习、合作交流、解决实际问题的能力。

三、说教学过程
整个教学流程，我分为五大环节，充分挖掘多媒体课件所蕴含的优势，围绕目标层层推进，既体现了重难点的把握，又有利于问题的解决。