受轴向拉力的轴径及螺纹计算

螺纹连接计算目录起重机设计规范（箱形梁计算） (2)附1 :螺栓的承载力 (2)㈠连接螺栓的抗剪承载力 (2)㈡螺栓连接的抗拉承载力 (3)㈢剪力和拉力共同作用下螺栓的承载力 (4)附2 :螺栓群计算 (4)㈠螺栓群轴心受剪 (4)㈡螺栓群偏心受剪 (4)㈢螺栓群在弯矩作用下受拉 (5)㈣螺栓群偏心受拉 (5)㈤螺栓群受拉力、弯矩和剪力共同作用 (5)㈥螺栓连接计算公式 (5)附3:螺旋螺纹连接（支撑） (5)㈠三角螺纹 (5)㈡梯形螺纹 (13)㈢螺旋调节压杆稳定性 (14)附4螺纹连接计算表格.xls (15)附5 PSB螺栓（杆）、销联接.xlsx (15)起重机设计规范(箱形梁计算)强度计算对于s/ b0.7的高强度钢材，基本许用应力计算：0. 5s0.35 b(28)剪应力许用应力计算：n3(29)端面承压许用应力cd计算：cd 1.4(30) 局部压应力Pmtc(31) 复合应力—2 2m m3 2(32) 两个方向的正应力2 2 x y3 2x y xy(33)验算焊缝复合应力:2 2.x y x y 2；yh(37)稳疋性计算受弯构件的整体稳定性H型钢或焊接工字钢⑴、载荷作用在受压翼缘上时，1b23513——. s2351334510. 729 ；⑵、载荷作用在受拉翼缘上时，丄20 2352352016.506 ；b丫s345⑶、跨中受压翼缘右侧向支承时，丄16 2352351613. 205。

b s345附1：螺栓的承载力㈠连接螺栓的抗剪承载力1•普通螺栓的抗剪承载力⑴按抗剪d 2N] % 丁[ j] (2 - 2 - 27))4n v ------- 剪切面数，单剪n v1双剪单剪n v2；d -------- 螺栓杆直径；[j] ----------- 螺栓的许用剪应力0. 6~0. 8如螺杆[j ] —，被连接构件[c ]1弋]n⑵按承压[N c ] d t [』(2-2-28))t ——承压构件的较小总厚 度；d ------ 螺栓杆直径；[c ]——孔壁的许用应力，[c ] 1冃] 2•摩擦型高强螺栓的抗剪承载力Z P[N v ]且一[j ] (2 - 2 - 29))nZ m ------------ 传力的摩擦面数；---- 摩擦系数，Q235(0.30 〜0.45) , Q345(0.35 〜0.55);P ——单个螺栓的预紧力， 预拉力P0.7 sl A ；sl——屈服点，A ——螺栓的有效截面n --------- 安全系数，载荷组合 A B C,安全系数n 1. 48、. 34、. 22表3-2-8 摩擦系数口值连接处构件接触面的处理方法 Q235 构件材料Q345及以上喷砂(喷砂后生赤锈)0.45 0.55 喷砂(或酸洗)后涂无机富锌漆 0.35 0.40钢丝刷清理浮锈或未处理的干净0.300.35轧制表面㈡螺栓连接的抗拉承载力1•普通螺栓的抗拉承载力抗拉 屈服点 157192245303353 459 561694817976 螺栓 等级强度Ysl螺栓公称直径(mm)等(Y b /KI/ rv'2 \ (N/mm 2)M16M18M20 M22 M24 M27 M30 M33M36 M39(N/mm)单个高强螺栓的预拉力 P (kN)8.8S > 800> 60070 86 110 135 158 205 250 310 366 437 10.9S > 1000 > 900 99 120 155 190 223 290 354 437 515 615 12.9S> 1200 > 1080110145185229267347424525618738表中预拉力值PA ，其中0.7slsl取各档中的最小3-2-9单个高强螺栓的预拉力d 2[N t] —M I](2 - 2 - 30)4d -------- 螺纹内径；[l] ------------ 螺栓的许用剪力2•摩擦型高强度螺栓的抗拉承载力㈡螺栓群偏心受剪螺栓强度：N iN iTx N iTy N iF 2 [N v ](2-2-41计算式对普通螺栓和高强度螺栓都适用。

15—4 一牵曳钩用2个M10的普通螺钉固定于机体上，如图所示.已知接合面间的摩擦系数f=0.15，螺栓材料为Q235、强度级别为4.6级，装配时控制预紧力，试求螺栓组连接允许的最大牵引力。

解题分析:本题是螺栓组受横向载荷作用的典型例子．它是靠普通螺栓拧紧后在接合面间产生的摩擦力来传递横向外载荷F R 。

解题时，要先求出螺栓组所受的预紧力，然后，以连接的接合面不滑移作为计算准则，根据接合面的静力平衡条件反推出外载荷F R 。

题15—4图解题要点：(1)求预紧力F ′：由螺栓强度级别4.6级知σS =240MPa,查教材表11-5（a ），取S=1.35，则许用拉应力： ［σ]= σS /S =240/1。

35 MPa=178 MPa ， 查（GB196—86）M10螺纹小径d 1=8.376mm由教材式(11—13）： 1.3F ′/（πd 21/4）≤[σ] MPa 得:F ′=[σ]πd 21/（4×1.3）=178 ×π×8。

3762/5.2 N =7535 N （2） 求牵引力F R :由式（11—25）得F R =F ′fzm/K f =7535×0。

15×2×1/1.2N=1883。

8 N (取K f =1。

2)分析与思考：（1）常用螺纹按牙型分为哪几种?各有何特点?各适用于什么场合?连接螺纹用什么牙型？传动螺纹主要用哪些牙型？为什么？答：根据牙型，螺纹可以分为三角形、矩形、梯形、锯齿形等。

选用时要根据螺纹连接的工作要求，主要从螺纹连接的效率和自锁条件两个方面考虑，结合各种螺纹的牙形特点。

例如三角形螺纹，由于它的牙形角α较大，当量摩擦角υρ也较大（βρυυcos arctan arctan ff ==），分析螺纹的效率()υρη+ψψ=tan tan 和自锁条件 Ψυρ≤,可知三角形螺纹效率较低,但自锁条件较好，因此用于连接。

螺纹扭矩和轴向力关系
螺纹扭矩和轴向力是机械设计中非常重要的两个参数，它们之间的关系对于机械的性能和寿命有着至关重要的影响。

在本文中，我们将探讨螺纹扭矩和轴向力之间的关系，并介绍一些常见的计算方法和应用。

我们需要了解什么是螺纹扭矩和轴向力。

螺纹扭矩是指在螺纹连接中，为了使螺纹紧固，需要施加的扭矩大小。

轴向力是指在螺纹连接中，由于螺纹的紧固作用，产生的沿轴向方向的力。

这两个参数的大小和方向都与螺纹的尺寸、材料、紧固方式等因素有关。

在实际应用中，螺纹扭矩和轴向力往往是同时存在的。

例如，在机械设备中，螺纹连接通常用于连接轴和轴套、法兰和管道等部件。

在这些连接中，螺纹扭矩和轴向力的大小和方向都会影响连接的紧固程度和稳定性。

那么，螺纹扭矩和轴向力之间有什么关系呢？一般来说，螺纹扭矩越大，产生的轴向力也就越大。

这是因为螺纹连接的紧固过程中，螺纹的扭转会产生摩擦力，从而使螺纹产生轴向拉力。

这个拉力的大小与螺纹扭矩成正比，因此，当螺纹扭矩增大时，轴向力也会随之增大。

在实际应用中，我们需要根据具体的情况来计算螺纹扭矩和轴向力的大小。

一般来说，可以采用经验公式或者数值模拟的方法来进行
计算。

例如，在螺纹连接中，可以根据螺纹的尺寸、材料、摩擦系数等因素来计算螺纹扭矩和轴向力的大小。

同时，还需要考虑连接的紧固方式、工作环境等因素对螺纹连接的影响。

螺纹扭矩和轴向力是机械设计中非常重要的参数，它们之间的关系对于机械的性能和寿命有着至关重要的影响。

在实际应用中，我们需要根据具体的情况来计算和控制螺纹扭矩和轴向力的大小，以确保连接的稳定性和可靠性。

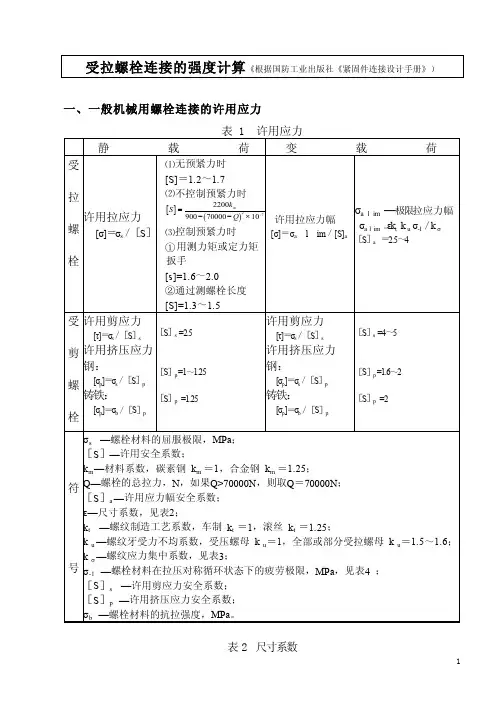
一、一般机械用螺栓连接的许用应力表2 尺寸系数二、松连接螺栓的强度计算一般机械用松连接螺栓，其螺纹部分的强度条件为：需要的计算直径为：式中： Q —螺栓的总拉力，此情况下是其工作拉力，N ；A c —螺栓螺纹部分的计算面积，（mm 2）； d c —螺纹部分的计算直径(mm)；d c =（d 2 + d 1 – H/6）/2≈d －0.94P ；其中： d 2和d 1 为螺纹的小径和大径，（mm ）,H 为螺纹牙理论高度，（mm ）, P 为螺纹螺距，（mm ）。

[σ]—松连接螺栓的许用拉应力，MPa 。

三、紧连接螺栓的强度计算1、只受预紧力的螺栓一般结构形式的螺栓螺母连接，螺栓除受预紧力外还受拧紧力矩的作用，综合考虑拉应力σ和扭转剪应力τ＝0.5σ，根据第四强度理论，可得螺纹部[]σπ≤=24c c d QA F[]σπQd c 4≥分的强度条件为：()[]στσσσσ2222330513+≈+≈≤..换算后得：[]4132⨯≤Q d cPπσ 螺栓需要的计算直径：[]d Q c P≥⨯413.πσ式中： Q P —螺栓的预紧力，N ；[σ]—静载紧连接螺栓的许用拉应力（按表1），MPa 。

当螺栓材料为低塑性材料时，如30CrMnSi 等，宜采用根据莫尔理论的强度条件：()()[]121121422-+++≤νσνστσ 式中：ν＝σSL /σSY ，对于一般塑性材料，ν＝1。

σSL 和σSY 分别是材料的拉伸、压缩屈服极限，MPa 。

2、受预紧力和静工作拉力的螺栓为保证连接的可靠性和充分发挥螺栓连接的潜力，螺栓的预紧应力σp 应在小于0.8σs 的条件下取较高值，对一般机械，σp ＝（0.5～0.7）σs 螺栓需要的预紧力：F C C C Q Q mb mP P ++'=螺栓总拉力：Q= Q p ’+F或表示为：Q Q C C C F P bb m=++ 式中： Q p —螺栓需要的预紧力，N ；Q p ’—被连接件中剩余预紧力（ 承受工作拉力后，被连接 件中剩余预紧力 Q p ’的推荐值见表5），N ； F —螺栓的工作拉力，N ；C b 、C m ─分别为螺栓和被连接件的拉、压刚度，均为定值。

一、矩形螺纹（牙型角α=0）螺纹副中，螺母所受到的轴向载荷Q 是沿螺纹各圈分布的，为便于分析，用集中载荷Q 代替，并设Q 作用于中径d 2圆周的一点上。

这样，当螺母相对于螺杆等速旋转时，可看作为一滑块(螺母)沿着以螺纹中径d 2展开，斜度为螺纹升角l 的斜面上等速滑动。

匀速拧紧螺母时，相当于以水平力推力F 推动滑块沿斜面等速向上滑动。

设法向反力为N ，则摩擦力为f N ，f 为摩擦系数，ρ 为摩擦角，ρ = arctan f 。

由于滑块沿斜面上升时，摩擦力向下，故总反力R 与Q 的的夹角为λ+ρ 。

由力的平衡条件可知，R 、F 和Q 三力组成力封闭三角形，由图可得：Qψd F使滑块等速运动所需要的水平力等速上升： Ft=Qtan(ф+ρ)等速上升所需力矩：T= Ftd 2/2= Qtan(ф+ρ)d 2/2等速下降： Ft=Qtan(ф—ρ)等速下降所需力矩：T= Ftd 2/2= Qtan(ф—ρ)d 2/2二、非矩形螺纹 螺纹的牙型角α≠0时的螺纹为非矩形螺纹。

非矩形螺纹的螺杆和螺母相对转动时，可看成楔形滑块沿楔形斜面移动；平面时法向反力N=Q; 平面时摩擦力F f =fN =fQ;楔形面时法向反力N /=Q/cosβ；楔形面摩擦力F f ! =f N/ =fQ/ cosβ;令f/ =f/ cosβ称当量摩擦系数。

F f ! =f /Q；楔形面和矩形螺纹的摩擦力相比，与当量摩擦系数对应的摩擦角称为当量摩擦角，用ρV 表示。

拧紧螺母时所需的水平推力及转矩：由于矩形螺纹与非矩形螺纹的运动关系相同，将ρV 代替ρ后可得：使滑块等速运动所需要的水平力等速上升： Ft=Qtan(ф+ρV )等速上升所需力矩： T= Ftd 2/2= Qtan(ф+ρV )d 2/2等速下降： Ft=Qtan(ф—ρV )等速上升所需力矩： T= Ftd 2/2= Qtan(ф—ρV )d 2/2三、螺纹联接的预紧螺纹联接 松联接——在装配时不拧紧，只存受外载时才受到力的作用——轻少用紧联接——在装配时需拧紧，即在承载时，已预先受力，预紧力Q P预紧目的：保持正常工作。

M8螺纹的轴向力一、M8螺纹概述M8螺纹是一种常用的机械紧固螺纹，其螺距为1.25mm，主要用于连接和紧固各种机械零部件。

M8螺纹具有较高的承载能力和良好的可靠性，因此在许多工程领域中得到了广泛应用。

二、轴向力的定义与产生轴向力是指作用在物体轴线方向上的力，通常用于描述旋转或直线运动的物体所受到的力。

在M8螺纹连接中，轴向力主要是由螺栓或螺柱受到预紧力或外部载荷而产生的。

预紧力是指在对螺栓或螺柱进行装配时施加的作用力，其目的是为了保证连接的紧密性和稳定性；外部载荷则是指在工作过程中螺栓或螺柱所受到的外部作用力。

三、M8螺纹轴向力的计算M8螺纹的轴向力可以通过以下公式进行计算：F=σ×d×n其中，F为轴向力，σ为螺栓材料的屈服强度，d为螺栓直径，n为螺栓数量。

根据不同的材料和工作环境，选择合适的屈服强度值进行计算，可以得出螺栓所承受的轴向力大小。

四、M8螺纹轴向力的影响因素M8螺纹轴向力的大小受到多种因素的影响，主要包括以下几个方面：1.材料性能：螺栓材料的屈服强度、弹性模量等力学性能对轴向力的大小有着直接的影响。

2.装配预紧力：通过控制装配预紧力的大小，可以调整螺栓所承受的轴向力。

预紧力越大，轴向力越大，连接越紧密，但过大的预紧力可能导致螺栓断裂或连接失效。

3.外部载荷：在工作过程中，螺栓所承受的外部载荷对其轴向力有明显影响。

需要根据工作实际情况合理选择螺栓规格和连接方式，以保证安全可靠的承载能力。

4.工作环境因素：如温度、腐蚀等环境因素也可能对螺栓的力学性能产生影响，从而影响其轴向力的大小。

需要在选择和使用螺栓时充分考虑这些因素的影响。

五、M8螺纹轴向力的实验研究为了进一步了解M8螺纹轴向力的实际表现和影响因素，需要进行实验研究。

通过实验测试不同材料、不同预紧力和不同外部载荷下的M8螺纹轴向力大小，可以获得更加准确和可靠的数据，为实际应用提供依据。

实验研究还可以对新型的M8螺纹连接方式进行评估和优化，以开发更加高效和可靠的连接方案。

第三章 螺纹联接（含螺旋传动）3-1 基础知识 一、螺纹的主要参数现以圆柱普通螺纹的外螺纹为例说明螺纹的主要几何参数，见图3-1，主要有：1）大径d ——螺纹的最大直径，即与螺纹牙顶重合的假想圆柱面的直径，在标准中定为公称直径。

2）小径1d ——螺纹的最小直径，即与螺纹牙底相重合的假想圆柱面的直径，在强度计算中常作为螺杆危险截面的计算直径。

3）中径2d ——通过螺纹轴向界面内牙型上的沟槽和突起宽度相等处的假想圆柱面的直径，近似等于螺纹的平均直径，2d ≈11()2d d +。

中径是确定螺纹几何参数和配合性质的直径。

４）线数n ——螺纹的螺旋线数目。

常用的联接螺纹要求自锁性，故多用单线螺纹；传动螺纹要求传动效率高，故多用双线或三线螺纹。

为了便于制造，一般用线数n ≤４。

５）螺距P ——螺纹相邻两个牙型上对应点间的轴向距离。

６）导程S ——螺纹上任一点沿同一条螺旋线转一周所移动的轴向距离。

单线螺纹S ＝P ，多线螺纹S ＝nP 。

７）螺纹升角λ——螺旋线的切线与垂直于螺纹轴线的平面间的夹角。

在螺纹的不同直径处，螺纹升角各不相同。

通常按螺纹中径2d 处计算，即22arctanarctan S nPd d λππ== （3-1） 图3-18）牙型角α——螺纹轴向截面内，螺纹牙型两侧边的夹角。

螺纹牙型的侧边与螺纹轴线的垂直平面的夹角称为牙侧角，对称牙型的牙侧角β＝α/2。

9）螺纹接触高度h——内外螺纹旋合后的接触面的径向高度。

二、螺纹联接的类型螺纹联接的主要类型有：1、螺栓联接常见的普通螺栓联接如图3-2a所示。

这种联接的结构特点是被联接件上的通孔和螺栓杆间留有间隙。

图3-2b是铰制孔用螺栓联接。

这种联接能精确固定被联接件的相对位置，并能承受横向载荷，但孔的加工精度要求较高。

图3-22、双头螺柱联接如图3-3a所示，这种联接适用于结构上不能采用螺栓联接的场合，例如被联接件之一太厚不宜制成通孔，且需要经常拆装时，往往采用双头螺柱联接。

一、矩形螺纹（牙型角α=0）螺纹副中，螺母所受到的轴向载荷Q 是沿螺纹各圈分布的，为便于分析，用集中载荷Q 代替，并设Q 作用于中径d 2圆周的一点上。

这样，当螺母相对于螺杆等速旋转时，可看作为一滑块(螺母)沿着以螺纹中径d 2展开，斜度为螺纹升角l 的斜面上等速滑动。

匀速拧紧螺母时，相当于以水平力推力F 推动滑块沿斜面等速向上滑动。

设法向反力为N ，则摩擦力为f N ，f 为摩擦系数，ρ 为摩擦角，ρ = arctan f 。

由于滑块沿斜面上升时，摩擦力向下，故总反力R 与Q 的的夹角为λ+ρ 。

由力的平衡条件可知，R 、F 和Q 三力组成力封闭三角形，由图可得：Qψd F使滑块等速运动所需要的水平力等速上升： Ft=Qtan(ф+ρ)等速上升所需力矩：T= Ftd 2/2= Qtan(ф+ρ)d 2/2等速下降： Ft=Qtan(ф—ρ)等速下降所需力矩：T= Ftd 2/2= Qtan(ф—ρ)d 2/2二、非矩形螺纹 螺纹的牙型角α≠0时的螺纹为非矩形螺纹。

非矩形螺纹的螺杆和螺母相对转动时，可看成楔形滑块沿楔形斜面移动；平面时法向反力N=Q; 平面时摩擦力F f =fN =fQ;楔形面时法向反力N /=Q/cosβ；楔形面摩擦力F f ! =f N/ =fQ/ cosβ;令f/ =f/ cosβ称当量摩擦系数。

F f ! =f /Q；楔形面和矩形螺纹的摩擦力相比，与当量摩擦系数对应的摩擦角称为当量摩擦角，用ρV 表示。

拧紧螺母时所需的水平推力及转矩：由于矩形螺纹与非矩形螺纹的运动关系相同，将ρV 代替ρ后可得：使滑块等速运动所需要的水平力等速上升： Ft=Qtan(ф+ρV )等速上升所需力矩： T= Ftd 2/2= Qtan(ф+ρV )d 2/2等速下降： Ft=Qtan(ф—ρV )等速上升所需力矩： T= Ftd 2/2= Qtan(ф—ρV )d 2/2三、螺纹联接的预紧螺纹联接 松联接——在装配时不拧紧，只存受外载时才受到力的作用——轻少用紧联接——在装配时需拧紧，即在承载时，已预先受力，预紧力Q P预紧目的：保持正常工作。

螺纹受力计算范文螺纹是一种常用的连接元件，广泛用于各种机械设备和构件的连接。

螺纹的受力计算是指在螺纹连接过程中，通过施加一定的力（拉力或扭矩）使螺纹连接紧固，在此过程中，需要计算螺纹所承受的力或应力，以保证连接的可靠性和安全性。

一、螺纹本身的受力计算螺纹本身所承受的受力主要包括轴向拉力和径向剪力。

1.轴向拉力的计算当螺纹连接紧固时，施加的外力作用在螺栓上，产生轴向拉力，使螺栓产生拉伸应力。

轴向拉力的计算可以通过以下公式得到：F=A*σ其中F为轴向拉力，A为螺纹截面的有效面积，σ为拉伸应力。

螺纹的轴向拉力应小于螺纹材料的抗拉强度，以保证螺纹的安全性。

2.径向剪力的计算当螺纹连接紧固时，施加的外力也会产生径向剪力，使螺纹产生剪应力。

径向剪力的计算可以通过以下公式得到：Ft=A*τ其中Ft为径向剪力，A为螺纹截面的有效面积，τ为剪应力。

螺纹的径向剪力应小于螺纹材料的剪切强度，以保证螺纹的安全性。

二、螺纹连接中的受力计算螺纹连接中的受力主要包括螺母的施力和螺栓的转矩。

1.螺母的施力计算螺母在螺纹连接中起到固定和紧固的作用，施加一定的力使螺纹连接紧固。

螺母的施力计算可以通过以下公式得到：F=T/(m*p)其中F为螺母的施力，T为螺纹连接中的转矩，m为螺纹的阻力系数，p为螺纹的截面径向上抗力系数。

2.螺栓的转矩计算螺栓在螺纹连接中起到传递力矩的作用，负责将外部的转矩传递到螺纹连接中。

螺栓的转矩计算可以通过以下公式得到：T=F*(m*p)其中T为螺纹连接中的转矩，F为螺母的施力，m为螺纹的阻力系数，p为螺纹的截面径向上抗力系数。

螺纹受力计算的目的是为了保证螺纹连接的可靠性和安全性，需要根据实际情况选择合适的材料和尺寸，以及合理的应力和载荷。

此外，还需要注意螺纹连接中的摩擦系数、摩擦力、螺母的刚度等因素的影响，并进行合理的校核和设计。

M3螺钉最大轴向力引言螺钉是机械连接中常用的元件，其承载能力是设计和安装的重要考虑因素之一。

对于M3螺钉而言，在设计和使用过程中，了解其最大轴向力是非常重要的。

本文将全面、详细、完整地探讨M3螺钉的最大轴向力。

螺纹连接的基本原理螺纹连接是一种常见的机械连接方式，它通过螺纹的摩擦力和扭矩传递力来实现零件的紧固。

M3螺钉的规格参数M3是一种标准扁平头螺钉，其规格参数包括螺纹直径、螺纹步距、螺纹长度等。

这些参数对于计算和确定螺钉的最大轴向力具有重要意义。

M3螺钉的最大承载力M3螺钉的最大承载力是指它能够承受的最大轴向力。

这个值常常由螺纹连接的强度决定，主要包括两个方面，即螺纹剪切强度和螺纹抗拉强度。

螺纹剪切强度螺纹剪切强度是指螺钉在受到轴向拉力作用时，螺纹剪切部分的最大承载力。

螺纹剪切强度可通过以下公式计算：螺纹剪切强度= π * (d/2)^2 * σ其中，d为螺纹直径，σ为材料的剪切强度。

螺纹抗拉强度螺纹抗拉强度是指螺纹承受拉力时，螺纹的最大承载力。

螺纹抗拉强度可通过以下公式计算：螺纹抗拉强度= π * (d/2)^2 * σt其中，d为螺纹直径，σt为材料的抗拉强度。

最大轴向力的确定最大轴向力是螺纹剪切强度和螺纹抗拉强度中较小的值。

因为在应用中，螺钉通常会承受拉力和剪切力，而较小的值可以确保螺纹不会破坏。

M3螺钉的应用注意事项在设计和使用M3螺钉时，还需要注意以下几个方面：材料选择螺钉的材料会影响其承载能力和耐久性。

常见的材料有碳钢、不锈钢等，根据具体的应用场景选择合适的材料是非常重要的。

扭矩控制螺钉的扭矩控制是保证螺纹连接质量的关键。

过大或过小的扭矩都会导致螺纹连接失效，因此需要根据设计要求和螺钉规格选择合适的扭矩值。

强度计算在特殊工况下，需要对螺钉的承载能力进行详细计算和验证。

这可以确保螺钉在特定应用条件下不会发生断裂或松动。

结论M3螺钉的最大轴向力是设计和使用过程中必须考虑的关键参数。

通过了解其规格参数、最大承载力以及应用注意事项，可以确保螺钉连接的安全可靠性。