蒲丰投针-2PPT课件

为宾客们做一次有趣的试验，他先在
一张白纸上画满了一条条距离相等的
数学家蒲丰 平行线。然后，他抓出一大把小针， (Buffon， 每根小针的长度都是平行线之间距离
Georges 的一半。蒲丰说：“请诸位把这些小
Louis） (1707-1788)
针一根一根地往纸上随便扔吧。”客
人们好奇地把小针一根一根地往纸上
在数学的天地里，重要 的不是我们知道什么，而是 我们怎么知道什么。
——毕达哥拉斯
义务教育课程标准实验教科书 九年级 上 册
6.2 投 针 试 验
温二十中
你闻到了吗？
相信自己，勇 敢的表达自己 的想法！
课外冲浪
蒲丰投针法国自然哲学家蒲丰先生经
常搞点有趣的试验给朋友们解闷。
1777年的一天，蒲丰先生又在家里
试验方式:小组合作交流,全班汇总试验验数据，达到数
据共享
试验工具:有距离为a平行线的纸,长度是l粗细均匀的针（l<a）
还有什么方面需要注意的吗？
Just do it!
每组至少完成100次试验 可采用不同的方式记录其中相交和不相交的次数 快速完成，争取名次 准确、美观、独特、创新…的制作表1
Just do it!
3.141 592 9 3.17 5
课外冲浪
用计算机实现统计模拟或抽 样，以获得问题的近似解，称为 蒙特卡罗(Monte Carlo)方法， 又称统计模拟法或统计试验法。 它是以概率和统计的理论为基础 的一种计算方法，他将所求解的 问题与一定的概率模型相联系。
我的课堂，我做主
小组讨论： 用几句话归纳这节课的几个环节
乱扔。
试一试 猜一猜
当针投到平行线的纸上时，会有什么情况出现？

该试验不仅在理论上具有重要意义，对 于理解随机性和几何规律的本质有重要 贡献，而且在实际应用中也有广泛的应
用价值。
蒲丰投针试验可以应用于统计学、物理 学、计算机科学等多个领域，为相关领
域的研究提供了重要的启示和工具。
蒲丰投针试验的局限性
01
02
03
04
蒲丰投针试验虽然是一个经典 的试验，但是它也存在一些局
针方向与平行线垂直。
重复投掷蒲丰投针N次，记录每 次投掷的结果。
测量与计算阶段
测量投掷后蒲丰投针 与平行线之间的距离 ，记录下来。
根据公式π=2*n/N ，计算π的近似值， 其中n为相交次数， N为投掷次数。
根据记录的数据，计 算蒲丰投针与平行线 相交的次数。
CHAPTER 03
试验结果分析
蒲丰投针试验的预期结果
蒲丰投针试验是一种估算π值的方法，其预期结果是通过投掷 一根针到一张白纸上，然后统计针与白纸边缘相交的次数， 来估算π的值。
蒲丰投针试验的预期结果是根据概率论和几何学原理推导出 来的，即当投掷次数足够多时，针与白纸边缘相交的频率接 近于π/4。
实际结果与预期结果的比较
在实际进行蒲丰投针试验时，需要记录针与白纸边缘相交的次数，并计 算出相应的π值。
限性。
首先，该试验的结果受到投针 方式、试验环境等因素的影响 ，可能导致结果存在误差。
其次，蒲丰投针试验的应用范 围相对有限，主要适用于一些 特定的几何形状和随机性问题
。
最后，蒲丰投针试验的结论仅 适用于理想化的模型，与实际
情况可能存在差异。
未来研究方向与展望
随着科学技术的发展和研究的深入， 蒲丰投针试验在未来仍有广阔的研究 前景。
蒲丰投针试验讲解课 件

投针试验的历史资料试验者年份投针次数n相交次数k的试验值wolf1850085000253231596smith1855063204121931554demorgan18606003833137fox1884075103048931595lazzerini19010833408180131415929reina1925054252085931795图11针与线相交图12投针试验样本空间及事件蒲丰投针实验蒲丰投针实验实验方案设针的中点与最近平行线的距离为y针与最近平行线的夹角为为横坐标y为纵坐标建立直角坐标系则每次掷针试验都随机地产生区域d中的一个点xy其中区域d为
>> n=40; >> p=1-nchoosek(365,n)*factorial(n)/365^n 运行结果： p= 0.8912
2．某接待站在某一周曾接待过 12 次来访，已知所有这 12 次接待 都是在周二和周四进行的， 问是否可以推断接待时间是有规定的？ >> p=2^12/7^12 %接待时间没有规定时， 访问都发生在周二和周四 的概率 运行结果： p= 2.9593e-007 此概率很小，由实际推断原理知接待时间是有规定的。
概率概念的要旨是在 17 世纪中叶法国数学家帕斯卡与 费马的讨论中才比较明确。他们在往来的信函中讨论" 合理分配赌注问题"， 在概率问题早期的研究中， 逐步建 立了事件、概率和随机变量等重要概念以及它们的基本 性质。后来由于许多社会问题和工程技术问题，如：人 口统计、保险理论、天文观测、误差理论、产品检验和 质量控制等， 这些问题的提出， 均促进了概率论的发展。
实验一
排列数与组合数的计算
【实验目的】 1．掌握排列数和组合数的计算方法 2．会用 Matlab 计算排列数和组合数 【实验要求】 1．掌握 Matlab 计算阶乘的命令 factorial 和双阶乘的命令 prod 2．掌握 Matlab 计算组合数的命令 nchoosek 和求所有组合的命令 combntns

2013-3-24
• 1850年，瑞士数学家沃尔夫在苏黎世，用 一根长36mm的针，平行线间距为45mm，投 掷5000次，得π ≈3.1596. • 1864年，英国人福克投掷了1100次，求得 π ≈3.1419.1901年，意大利人拉泽里尼投 掷了3408次，得到了准确到6位小数的π 值 .
2013-3-24
• 其中投针问题可述为：设在平面上有一组
平行线，其距都等于D，把一根长l<D的针 随机投上去，则这根针和一条直线相交的 概率是2l/π D.由于通过他的投针试验法可 以利用很多次随机投针试验算出π 的近似 值，所以特别引人瞩目，这也是最早的几 何概率问题.并且蒲丰本人对这个实验给予 证明。
2013-3-24
在考虑一个以r(r <l/2)为半径的硬币与平 面上画有间距为l的平行线相交的概率时, 假设硬币的周长为c, c=2π r, 则其概率结 果可以改写成: P0 =2r/ l =2π r/ (π l) =c/ (π l).
• 从上面的结果发现, 它们的形式是一 样的, 都是周长除以π l的形式，本小 组从中得到启发: 在蒲丰问题中, 对 投掷一个一般的凸多边形来说, 它与 平行线相交的概率可能与这个凸多边 形的周长密切相关.
2013-3-24
蒲丰投针问题研究史
• 蒲丰是几何概率的开创者，并以蒲丰投针
问题闻名于世，发表在其1777年的论著《 或然性算术试验》中.其中首先提出并解决 下列问题：把一个小薄圆片投入被分为若 干个小正方形的矩形域中，求使小圆片完 全落入某一小正方形内部的概率是多少， 接着讨论了投掷正方形薄片和针形物时的 概率问题.这些问题都称为蒲丰问题.
2013-3-24
• 解 1) 和三角形与平行线相交的讨论相似, 四边形与平行 线相交也有5种情形: • ①四边形只有一个顶点在一条平行线上(1个交点) (如图(a)） • ②四边形有两条边分别与平行线相交(2个交点) (如图(b)）； • ③平行线过四边形的对角线(2个交点) (如图(c)); • ④四边形的某一顶点恰好在平行线上, 其对应的某一边也 在同一条平行线上(2个交点) (如图(d)); • ⑤四边形的某一条边与平行线重合(无穷多个交点) (如图 (e)).

在数学的天地里，重要 的不是我们知道什么，而是 我们怎么知道什么。
——毕达哥拉斯
义务教育课程标准实验教科书 九年级 上 册
6.2 投 针 试 验
温二十中
你闻到了吗？
相信自己，勇 敢的表达自己 的想法！
课外冲浪
蒲丰投针法国自然哲学家蒲丰先生经
常搞点有趣的试验给朋友们解闷。
1777年的一天，蒲丰先生又在家里
乱扔。
； 欧洲杯直播/
；
可当他快到终点时，才发现机会全错过了。 第三个弟子吸取了前边两个弟子的教训。当走过全程三分之一时，即分出大中小三类；再走三分之一时，验是否正确；等到最后三分之一时，他选择了属于大类中的一个美丽的穗。虽说，这穗不是田里最好最大的一个，但对他来说，已经 是心满意足了。 137、科学史上因语文而失误例谈 ①美国化学家路易斯于1916年在一篇中提出了共价键理论，但在本世纪20年代曾一度被称为朗缪尔理论。原因是路易斯虽很聪明，但性格内向，不善言谈，他提出功价键理论后，并未引起多大反响。致使这一理论濒临泯灭的困 境。幸亏三年后，一位思想敏锐的化学家朗缪尔看出了共价键理论的重大意义，于是，一方面凭借生动活泼流畅的文笔在有影响的《美国化学学会志》等刊物发表系列，一方面又以滔滔不绝的口才在国内大型学术会议上多次发表演说，终于使这一理论走出了困境，得到普遍承认。 ②现在举世公认，美国科学家维纳是信息论的创始人，因为他在上世纪50年代对信息论做了系统阐述，并建立了维纳滤波理论和信号预测论。可早在30年代就提出信息论的竟是中国数学家申农。最先提出信息论的却没有成为创始者，其原因固然很复杂，但有一点可以肯定，申农未能充分 利用语文工具对信息论进行系统阐述和广泛宣传，该是原因之一。 ③著名物理学家法拉第，早在1873年就已经发现了电磁感应现象，但由于他在论述这一现象时，用语晦涩，致使这项重大的科学发现在长达26年的确时间里被束之高阁。后来幸亏了酷爱诗歌的物理学家麦克斯韦以他 特有的形象思维和精练的语言，把它描述出来，才使这一重大科学发现公之于众。 138、老报纸的价值 旧报纸，若是卖给收废品的，一斤大约三四毛钱。 但吴江路就有一家老报纸馆专营《人民日报》、《光明日报》、《解放军报》和《文汇报》等老报纸，上世纪60年代的 普通报纸，每张要卖218元，就是上世纪80年代的普通报纸，每张也要卖128元。那些按理说没有收藏价值的普通旧报纸居然还卖得挺火。 原来，商家打出的宣传是这样的：为自己或者是亲人卖一份生日老报纸吧！颜色已发黄的老报纸配以充满怀旧情调的包装，就有一些历史韵味。 顾客主要是二三岁的市民，他们或者购买自己出生那一天的报纸，看看自己出生那天世界发生了哪些事，或者卖来赠送给长辈，以引起长辈对青春的记忆。 这老板叫刘德保，素有收集老报纸的兴趣。他将老报纸的卖点定位于生日礼物上，可谓别出心裁，既雅致，又有韵味；既可以 满足青年人对出生那个年代的好奇，又会唤起中老年人对逝去岁月的缅怀。三四毛钱一斤的旧报纸得以卖出每张一二百元的高价，价钱翻了千倍以上，可谓极高附加值了！ 139、最大的不幸 一个人在他23岁时为人陷害，在牢房里呆了9年，后来冤案告破，他终于走出了监狱。出 狱后，他开始了常年如一日的反复控诉、咒骂：“我真不幸，在最年轻有为的时候竟遭受冤屈，在监狱度过本应最美好的一段时光。那样的监狱简直不是人居住的地方，狭窄得连转身都困难。唯一的细小窗口里几乎看不到星点灿烂的阳光，冬天寒冷难忍；夏天蚊虫叮咬……真不明白，上 帝为什么不惩罚那个陷害我的家伙，即使将千刀万剐，也难以解我心头之恨啊！” 73岁那年，在贫病交加中，他终于卧床不起。弥留之际，牧师来到他的床边：“可怜的孩子，去天堂之前，忏悔你在人世间的一切罪恶吧……”牧师的话音刚落，病床上的他声嘶力竭地叫喊起来： “我没有什么需要忏悔，我需要的是诅咒，诅咒那些施予我不幸命运的人……” 牧师问：“您因受冤屈在监狱呆了多少年？离开监狱后又生活了多少年？”他恶狠狠地将数字告诉了牧师。 牧师长叹了一口气：“可怜的人，您真是世上最不幸的人，对您的不幸，我真的感到万分 同情和悲痛！但他人囚禁了你区区9年，而当你走出监牢本应获取永久自由的时候，您却用心底里的仇恨、抱怨、诅咒囚禁了自己整整41年！” 140、索尼：不迷信专家 近几年，日本索尼公司在招聘大学生时，对学校名称采取“不准问，不准说，不准写”的“三不”方针。公司认为， 在激烈竞争和多变时代，企业需要各种人才，只有将各种不同的人聚集在一起，才能更好地发挥创造性，开发出新产品。只在少数名牌大学中招聘人才，会使企业失去活力。索尼公司的创始人之一的井深大说：“我从不迷信专家，专家倾向于争辩你为什么不做或不能做某种事情，而我们 经常强调的是从无到有去实干。”因此，索尼喜欢思想敏锐、不墨守成规、勇于探索创新的人，他们鼓励科技人才“跳槽”，可以在公司任何部门寻找新的职位，“毛遂自荐”参与项目的开发研究。公司认为，这种人思想开放，思维活跃，兴趣广泛，具有创造意识和创新精神，是实干家 而不是空谈家，有培养和发展前途，应加以重用。 141、神奇的皮鞋 多明尼奎?博登纳夫，是法国一位年轻企业家、艺术家。他所经营的公司历来就是发展美术业，但始终都是没有看到兴旺的一天。 一天，他在徒步回家的路上，突然，感到脚下有什么绊了一下，低头一看，原 来是一只破旧皮鞋，他刚想抬起脚将它踢开，却又发现这只鞋有几分像一张皱纹满布的人脸。一个艺术的灵感刹那间在他脑海里闪现，他如获至宝，于是赶忙将破旧皮鞋拾起，迫不及待地跑回家，将其改头换面，变成了一件有鼻有眼有表情的人像艺术品。 以后，博登纳夫又陆续捡 回一些残旧破皮鞋，经过他那丰富的想象力和神奇的艺术之手再加工，一双双被遗忘的“废物”先后变成奇妙谐趣的皮鞋脸谱艺术品。后来，博登纳夫在巴黎开设了皮鞋人像艺术馆，引起了轰动，生意异常兴隆。 看来，在现实生活中，在许多人不屑一顾的小小事情里，往往都隐藏 着成功的契机。当然，要获成功，得靠用心发掘。博登纳夫的这一成功，无疑就在于他比别人多了一个“艺术”心眼。 142、我们到底有多美 世界著名法学家德沃金先生到中国一游，并在几所著名法学院巡回讲演。在一次讲演后，与学生们青春激扬的问答恰恰相反，有一个蠢 货突然发问：“你对我们这所大学如何看？”他到这个学校，准确地说，到这个梯形教室，只有几十分钟，始则略有诧异，继则笑笑，充满理解地笑笑，说：“这是个极好的大学！”——他还能说什么呢？！ 这是时下的一种通病。有些人见到洋人，尤其是见到欧美来的西洋人，便 非要拉住人家的手问长问短，非要请教别人自己美不美，非要请教别人我们这里是不是好山好水好地方。真的不懂，我们的学子从幼儿园起就接受爱国主义教育，居然仍旧如此不自信。 但凡有人以中国特色为名，拒绝外国的时候，被拒绝的大多是比较先进的，也是比较合理的。相 反，学习外国坏东西的时候，我们大多不谈中国特色。鼓励汽车消费时也不谈中国特色。养狗成风时也不谈中国特色。近年来中国兴起了养狗热潮，说是西洋人也喜欢养狗，因为狗是人类的朋友。但西洋人有导盲犬，我们有吗？没有。反正街上是见不到一条导盲犬。 143、以德报怨 没有社会效用 过去我们一直以为“以德报怨”是最高的道德境界，可是关于德怨相报的经济学分析却表明，以德报怨的社会效用为0分，一个小偷被抓到了，报之以德，会给他一个错误的暗示，结果鼓励他错上加错。如有人问孔子：“以德报怨，会怎么样呢？”孔子答：“怎么会用 德去报怨呢？！应当以直报怨。报德的对象只能是德而不是怨。”孔子对如何抱怨的方案是“直”，它可以理解为，一是要用正直的方式对待破坏规则的人，二是要直率地告诉对方，你什么地方做错了事。经济学家认为，以直报怨的社会效用是1分，以直报怨的人，既不想迎合你（报 德）；也不想报复你（报怨）；而是让你知道错在哪里，犯了什么规。在道德的范畴内，这种方式也是满不错的。 最糟糕的是以怨报怨，怨怨相报，只能两败俱伤，所以经济学分析给它打了-2分。 144、钱学森的“大成智慧学” 《日报?理论周刊》4月12日刊登中国人民大 学教授钱学敏的文章，介绍了钱学森的“大成智慧学”。 钱老曾说：“人的智慧是两大部分：量智和性智。缺一不成智慧！此为‘大成智慧学’。”什么是“量智”和“性智”呢？钱老认为，现代科学技术体系中的数学科学、自然科学、系统科学、军事科学、社会科学、思维科学、 人体科学、地理科学、行为科学、建筑科学等10大科学技术部门的知识是性智、量智的结合，主要表现为“量智”；而文艺创作、文艺理论、美学以及各种文艺实践活动，也是性智与量智的结合，但主要表现为“性智”。“性智”、“量智”是相通的。 钱老说：“‘量智’主要是 科学技术，是说科学技术总是从局部到整体，从研究量变到质变，‘量’非常重要。当然科学技术也重视由量变所引起的质变，所以科学技术也有‘性智’，也很重要。大科学家就尤其要有‘性智’。‘性智’是从整体感受入手去理解事物，是从‘质’入手去认识世界。中医理论就如此， 从‘望、闻、问、切’到‘辨施治’，但最后也有‘量’，用药都定量的嘛。” 关于“量智”与“性智”、逻辑思维与形象思维不可分离及其在科学与艺术创作过程中的作用，钱老分析：“从思维科学角度看，科学工作总是从一个猜想开始的，然后才是科学论；换言之，科学工作 是源于形象思维，终于逻辑思维。形象思维是源于艺术，所以科学工作是先艺术，后才是科学。相反，艺术工作必须对事物有个科学的认识，然后才是艺术创作。在过去，人们总是只看到后一半，所以把科学和艺术分了家，而其实是分不了家的；科学需要艺术，艺术也需要科学。” 145、平常心 三伏天，禅院的草地枯黄了一大片。“快撒些草籽吧，好难看啊！”小和尚说。“等天凉了。”师父挥挥手，“随时。” 中秋，师父买了一大包草籽，叫小和尚去播种。秋风突起，草籽飘舞。“不好，许多草籽被吹飞了。”小和尚喊。“没关系，吹走的多半是空 的，撒下去也不会发芽。”师父说，“随性。” 撒完草籽，几只小鸟即来啄食。“要命了！草籽都被鸟吃了！”小和尚急得跳脚。“没关系，草籽多，吃不完！”师父继续翻着经书，“随遇。” 半夜一场骤雨。一大早，小和尚冲进禅房：“师父！这下完了，好多草籽被雨水冲 走了！”“冲到哪儿，就在哪儿发芽！”

/4.因为对于每一个z，这个概率都为（π-2）/4，因此对于任意的正数x，y，z，有P=（π-2）/4，命题得证。

为了估算π的值，我们需要通过实验来估计它的概率，这一过程可交由计算机编程来实现，事实上x+y>z，x&sup2;+y&sup2；﹤z&sup2；等价于（x+y-z）（x&sup2;+y&sup2;-z&sup2；）﹤0，因此只需检验这一个式子是否成立即可。

若进行了m 次随机试验，有n次满足该式，当m足够大时，n/m趋近于（π-2）/4，令n/m=（π-2）/4，解得π=4n/m+2，即可估计出π值。

值得注意的是这里采用的方法：设计一个适当的试验，它的概率与我们感兴趣的一个量（如π）有关，然后利用试验结果来估计这个量，随着计算机等现代技术的发展，这一方法已经发展为具有广泛应用性的蒙特卡罗方法。

计算π最稀奇方法之一计算π的最为稀奇的方法之一，要数18世纪法国的博物学家C·布丰和他的投针实验：在一个平面上，用尺画一组相距为d的平行线；一根长度小于d的针，扔到画了线的平面上；如果针与线相交，则该次扔出被认为是有利的，否则则是不利的．布丰惊奇地发现：有利的扔出与不利的扔出两者次数的比，是一个包含π的表示式．如果针的长度等于d，那么有利扔出的概率为2/π．扔的次数越多，由此能求出越为精确的π的值．公元1901年，意大利数学家拉兹瑞尼作了3408次投针，给出π的值为3．1415929——准确到小数后6位．不过，不管拉兹瑞尼是否实际上投过针，他的实验还是受到了美国犹他州奥格登的国立韦伯大学的L·巴杰的质疑．通过几何、微积分、概率等广泛的范围和渠道发现π，这是着实令人惊讶的！证明下面就是一个简单而巧妙的证明。

找一根铁丝弯成一个圆圈，使其直径恰恰等于平行线间的距离d。

可以想象得到，对于这样的圆圈来说，不管怎么扔下，都将和平行线有两个交点。

鼓一响，法律无声。——英国 2、任何法律的根本；不，不成文法本 身就是 讲道理 ……法 律，也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正，其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等，但是在法律 面前人 人是平 等的。 ——波 洛克
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！

首先 ，从数学的角度看是什么因素决定针 与平行线是否相交 ？
这是数学建模的第一步。看下面这 张投针 的示意 图
图２
这里呈现了三种相交和两种不相交的情 况。看来 ， 与平行线 针
是否相交是 由两个因素决定 的 ： 一是投 针的位置， 二是投针 的方 向。
我们 可以用针的中点到离它最近的平行线 的距离 ｘ 刻画针 的位置 ，
动画软件平台难以实现的。这类课 件极大地丰富了教学资 源， 有效
这个实验给 出了一个全新的利用概率思想计算 叮 的近似值的 ｒ 方法 ， 后来这种方法发展成为利用计算机模拟解决数学和物理问题
的重要方法之一—蒙特卡罗方法 （ ＭＣ） 介绍这 个实验 不仅可 以提 。 高学生学 习概率 的兴趣 ， 而且加深学生对 概率 的认识 ， 更能初 步体 会到计算机是当今科学研究的重要工具 。
维普资讯
敏 毛 Ｃ
２０． ０７ ８
（ 下旬刊 ）
现代信 息技术在 中学概率教学 中 的应 用 ： 蒲丰投针 实验
口 王
中图分类号 ቤተ መጻሕፍቲ ባይዱ ４ Ｇ６ ２ 文献标识码 ： Ａ
培
湖北 ・ 汉 武 ４ ０７） ３ ０９
文章编号 ：６ ２ ７ ９ （ ０ ７） ８ ０ ５ ０ １７ － ８ ４ ２ ０ ０— ６— ２
用平行线从左 向右的方向与针向上 的方向形成的夹角 ０刻画针 的
方 向 （ 图 ） 如 ，
图 １
学教育软件 《 超级画板 》 开发 制作而成 的。 对于广 大教师 来说 ，
只需要在课堂上运行这 个课 件就行 了， 用起来十分方便 ， 使 不需 要 经过技术培训 。下 图是这个课件 的运行效 果图 ，显示 了实验 经过 ２１ ０ 次的结果 ， 中红针表示针与平行 线相交 。 其 当然 ， 如果觉得实验 次数太少 ， 以通过 鼠标选择 相应按钮 重 可 新开始实验 ， 直到你所满意的次数 ， 以调节针的长度。类似地 ， 还可

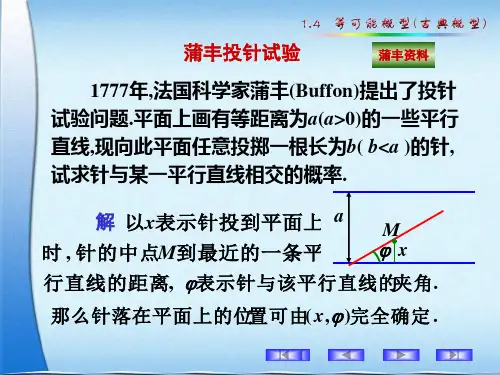
投针试验投针问题1777年法国科学家布丰提出的一种计算圆周率的方法——随机投针法，即著名的布丰投针问题。

投针步骤这一方法的步骤是：1）取一张白纸，在上面画上许多条间距为a的平行线。

2）取一根长度为l（l<a）的针，随机地向画有平行直线的纸上掷n次，观察针与直线相交的次数，记为m3）计算针与直线相交的概率．18世纪，法国数学家布丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为a的平行线，将一根长度为l（l<a）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。

”布丰本人证明了，这个概率是p=2l/（πd) π为圆周率利用这个公式可以用概率的方法得到圆周率的近似值。

下面是一些资料试验者时间投掷次数相交次数圆周率估计值Wolf1850年5000 2532 3.1596Smith 1855年3204 1218.5 3.1554C.De Morgan 1680年600 382.5 3.137Fox1884年1030 489 3.1595Lazzerini 1901年3408 1808 3.1415929Reina 1925年2520 859 3.1795设这三个正数为x，y，z，不妨设x≤y≤z，对于每一个确定的z，则必须满足x+y>z，x&sup2;+y&sup2；﹤z&sup2；，容易证明这两个式子即为以这3个正数为边长可以围成一个钝角三角形的充要条件，用线性规划可知满足题设的可行域为直线x+y=z与圆x&sup2;+y&sup2;=z&sup2；围成的弓形，总的可行域为一个边长为z的正方形，则可以围成一个钝角三角形的概率P=S弓形/S正方形=（πz&sup2;/4-z&sup2;/2）/z&sup2;=（π-2）/4.因为对于每一个z，这个概率都为（π-2）/4，因此对于任意的正数x，y，z，有P=（π-2）/4，命题得证。

π的试验值
3.159 6 3.155 4 3.137 3.159 5 3.141 592 9 3.17 5
课外冲浪
用计算机实现统计模拟或抽 样，以获得问题的近似解，称为 蒙特卡罗(Monte Carlo)方法， 又称统计模拟法或统计试验法。 它是以概率和统计的理论为基础 的一种计算方法，他将所求解的 问题与一定的概率模型相联系。
好好学习，天天向上。
准确、美观、独特、创新…的制作表1
Just do it!
分工合作：统计全班的试验数据 实验次数 200 400 600 800 1000 1200 1400 1600 1700
相交频数 相交频率
请每组同学利用全班的试验数据制作折线统计图； 通过本次试验、统计的过程，你什么发现和感想吗？
投针试验的历史资料
我的课堂，我做主
小组讨论： 用几句话归纳这节课的几个环节 完成了这节课的学习，对我影响最深的学 习体验是什么？
这节课还存在的疑惑是什么？又将如何去解决？
课外冲浪
最后蒲丰宣布结果：大家共投针2212次， 其中与直线相交的就有704次。用704去除2212， 得数为3.142。他笑了笑说：“这就是圆周率π 的近似值。”这时，众宾客哗然：“圆周率π? 这根本和圆沾不上边呀?”蒲丰先生却好像看透 了众人的心思，斩钉截铁地说：“诸位不用怀 疑，这的确就是圆周率π的近似值。你们看，连 圆规也不要，就可以求出π的值来。只要你有耐 心，投掷的次数越多，求出的圆周率就越精 确。”这就是数学史上有名的“投针试验”。
试验者
Wolf Smitn C.Dg morgan Fox Lazzerini Reina
时间
1850年 1855年 1860年 1884年 1901年 1925年

2
P(
A)
μ(G ) μ( S )
G的面积 S的面积
π b sind
02 aπ 2
a
b
π
2b aπ
.
o
2
蒲丰投针试验的应用及意义
P( A) 2b aπ
根据频率的稳定性, 当投针试验次数n 很大时,
测出针与平行直线相交的次数m , 则频率值m即可 n
作为 P( A) 的近似值代入上式, 那么
那么针落在平面上的位置可由( x, )完全确定 .
投针试验的所有可能结果与
矩形区域
a M
S {(x, ) 0 x a,0 π}
x
2
中的所有点一一对应.
由投掷的任意性可知
这是一个几何概型问题.
所关心的事件
o
A { 针与某一平行直线相交}
发生的充分必要条件为S 中的点满足
0 x b sin , 0 π .
蒲丰投针试验
蒲丰资料
1777年,法国科学家蒲丰(Buffon)提出了投针 试验问题.平面上画有等距离为a(a>0)的一些平行 直线,现向此平面任意投掷一根长为b( b<a )的针, 试求针与某一平行直线相交的概率.
解 以x表示针投到平面上 a M
时 , 针的中点M到最近的一条平
x
行直线的距离, 表示针与该平行直线的夹角.
m 2b π 2bn .
n aπ
am
利用上式可计算圆周率π 的近似值 .
历史上一些学者的计算结果(直线距离a=1)
试验 Wolf
时间 (年）
1850
针长 0.8
投掷次数 相交次数 π的近似值
5000
2532 3.1596

蒲丰投针试验与π学科：《数学史》作者：***班级：07级数本班学号：********蒲丰投针试验和π作者：*** 班级：07级数本班 学号：******摘要：“圆周率”是指一个圆的周长与其直径的比值。

古今中外，许多人致力于圆周率的研究与计算。

为了计算出圆周率的越来越好的近似值，一代代的数学家为这个神秘的数贡献了无数的时间与心血。

公元1777年，法国数学家、自然科学家蒲丰利用很多次随机投针试验算出π的近似值，引起广泛关注，这也是最早的几何概率问题，并且蒲丰本人对这个实验给予了证明。

计算π的这一方法，不但因其新颖，奇妙而让人叫绝，而且它开创了使用随机数处理确定性数学问题的先河，是用偶然性方法去解决确定性计算的前导。

关键字：π 蒲丰 蒲丰投针试验 几何概率因为任何两个圆都相似，故所有圆的周长和它的直径的比都等于同一常数，我们把这一常数叫“圆周率”。

国际上，人们习惯地把圆周率用符号π表示。

1600年，英国的威廉·奥托兰特首先使用πδ表示圆周率，他的理由是，因为π是希腊文圆周的第一个字母，奥托兰特用它来表示圆周长，而δ是希腊文直径的第一个字母，奥托兰特用它来表示直径，根据圆周率的定义，理应用πδ表示圆周率，但在推算圆周率的过程中，人们常用直径为1的圆，即令1δ=，这样πδ就等于π了。

1706年英国的琼斯首先改用π表示圆周率，后来被数学家广泛接受，一直沿用至今。

古今中外，许多人致力于圆周率的研究与计算。

为了计算出圆周率的越来越好的近似值，一代代的数学家为这个神秘的数贡献了无数的时间与心血。

回顾历史，人类对π的认识过程，反映了数学和计算技术发展情形的一个侧面。

π的研究，在一定程度上反映这个地区或时代的数学水平。

德国数学家康托说：“历史上一个国家所算得的圆周率的准确程度，可以作为衡量这个国家当时数学发展水平的指标。

”1874年勒让德证明了π和π都是无理数，即不能用两个整数的比表示．1882年德国数学家林德曼证明了π是超越数，即不可能是一个整系数代数方程的根，尽管如此，自古至今，很多人都在用各种方法求π的近似值。

蒲丰投针试验
蒲丰资料
1777年,法国科学家蒲丰(Buffon)提ห้องสมุดไป่ตู้了投针 试验问题.平面上画有等距离为a(a>0)的一些平行直 线,现向此平面任意投掷一根长为b( b<a )的针,试求 针与某一平行直线相交的概率. 解 以 x表示针投到平面上时,
针的中点M到最近的一条平行
a
M x
直线的距离, 表示针与该平行直线的夹角.
1.0
0.75 0.83 0.5419
600
1030 3408 2520
382
489 1808 859
3.137
3.1595 3.1415929 3.1795
利用蒙特卡罗(Monte Carlo)法进行计算机模拟. 单击图形播放/暂停 ESC键退出 取a 1, b 0.85.
利用上式可计算圆周率π 的近似值.
历史上一些学者的计算结果(直线距离a=1)
试验者 Wolf Smith 时间 1850 1855 针长 0.8 0.6 投掷次数 相交次数 π的近似值 5000 3204 2532 1218 3.1596 3.1554
De Morgan 1860
Fox Lazzerini Reina 1884 1901 1925
那么针落在平面上的位置可由( x , )完全确定.
投针试验的所有可能结果与 矩形区域
a S {( x , ) 0 x ,0 π} 2 中的所有点一一对应 . 由投掷的任意性可知 这是一个几何概型问题.
a
M x
所关心的事件
o
A { 针与某一平行直线相交} 发生的充分必要条件为S 中的点满足 b 0 x sin , 0 π . 2

斯密思（Smith） 投计次数：3204次 pi的实验值：3.1553
2021/3/10年9月2日
Monte Carlo方法的发展历史
▪ 20世纪四十年代，由于电子计算机的出现，利用电子计算机可以实 现大量的随机抽样的试验，使得用随机试验方法解决实际问题才有 了可能。其中作为当时的代表性工作便是在第二次世界大战期间， 为解决原子弹研制工作中，裂变物质的中子随机扩散问题，美国数 学家冯.诺伊曼和乌拉姆等提出蒙特卡罗模拟方法.由于当时工作是保 密的，就给这种方法起了一个代号叫蒙特卡罗，即摩纳哥的一个赌 城的名字。用赌城的名字作为随机模拟的名称，既反映了该方法的 部分内涵，又易记忆，因而很快就得到人们的普遍接受。
2021/3/10年9月2日
Monte Carlo方法的基本思想
▪ 蒙特卡罗方法又称计算机随机模拟方法。它是以概 率统计理论为基础的一种方法。
▪ 由蒲丰实验可以知道，当所求问题的解是某个事件 的概率，或者是某个随机变量的数学期望，或者是 与概率、数学期望有关的量时。通过某种试验的方 法，得出该事件发生的频率，或者该随机变量若干 个具体观察值的算术平均值，通过它得到问题的解。 这就是蒙特卡洛方法的基本思想。
Monte Carlo方法的发展历史
历史上的实验
1901
1850
沃尔弗（Wolf） 投计次数：5000次 pi的实验值：3.1596
1855
1894
拉查里尼（Lazzarini） 投计次数：3408次 pi的实验值：3.141592
福克斯（Fox） 投计次数：1120次 pi的实验值：3.1419
2021/3/10年9月2日
例.蒲丰氏问题
▪ 设针投到地面上的位置可以用一组参数 （x,θ）来描述,x为针中心的坐标,θ为针 与平行线的夹角,如图所示。

蒲丰投针实验样本空间的度量蒲丰投针实验是一种用于估计圆周率的经典实验。

在这个实验中，我们将一根长度为L的针随机地投掷到一块平面上，该平面上有一系列平行线，这些线之间的距离为d（d大于等于L）。

实验的目标是通过统计针与线相交的次数来估计圆周率π的值。

样本空间是指所有可能结果组成的集合。

在蒲丰投针实验中，样本空间可以定义为所有可能的针与线相交或不相交情况的集合。

为了更好地理解样本空间及其度量，在下面我们将对蒲丰投针实验样本空间进行详细讨论。

1. 针与线是否相交：- 相交：当针与至少一条线相交时，记为事件A。

- 不相交：当针没有与任何线相交时，记为事件B。

2. 针与线相交的方式：- 完全横过：当针完全横过一条线时，记为事件C。

- 仅部分横过：当针只横过部分线时，记为事件D。

3. 针与线相交位置：- 针中心距离最近线段较远端点小于L/2：记为事件E。

- 针中心距离最近线段较远端点大于等于L/2：记为事件F。

通过对样本空间的划分，我们可以得到以下事件的关系：- 事件A = 事件C + 事件D- 事件D = 事件E + 事件F在蒲丰投针实验中，我们通常关注的是针与线相交的次数。

通过统计相交次数和总投掷次数之比，可以得到圆周率π的估计值。

这个估计值可以用以下公式表示：π ≈ (2L)/(d * P(A))其中，P(A)是事件A发生的概率，即针与线相交的概率。

P(A)可以通过实验中统计相交次数和总投掷次数之比来估计。

在进行蒲丰投针实验时，我们需要选择合适的样本空间度量来确保结果的准确性。

常见的度量方式包括：1. 针长L：针长是一个重要的度量因素，它决定了针能否完全横过一条线。

选择合适的针长对于结果准确性至关重要。

2. 线间距d：线间距也是一个重要因素，它决定了针与线相交的概率。

选择合适的线间距可以使实验结果更加稳定和准确。

3. 投掷次数：进行足够多的投掷次数可以增加统计结果的可靠性。

通常，我们会进行大量的投掷以获得更准确的圆周率估计值。

3.口袋中有５张完全相同的卡片，分别写有 １cm,2cm,3cm,4cm,5cm.口袋外有２张卡片， 分别写有４cm,5cm.现随机从袋内取出一张 卡片，与口袋外两张卡片放在一起，以卡 片上的数量分别为三条线段的长度，回答 下列问题： （１）求这三条线段能构成三角形的概率 （２）求这三条线段能构成直角三角形的概 率 （３）求这三条线段能构成等腰三角形的概 率
7. （2012贵州遵义10分）如图，4张背面完全相 同的纸牌（用①、②、③、④表示），在纸牌的 正面分别写有四个不同的条件，小明将这4张纸牌 背面朝上洗匀后，先随机摸出一张（不放回）， 再随机摸出一张． （1）用树状图（或列表法）表示两次摸牌出现的 所有可能结果； （2）以两次摸出牌上的结果为条件，求能判断四 边形ABCD是平行四边形的概率．
4. （2012贵州贵阳10分）在一个不透明的口袋里有分别 标注2、4、6的3个小球（小球除数字不同外，其余都相 同），另有3张背面完全一样、正面分别写有数字6、7、 8的卡片．现从口袋中任意摸出一个小球，再从这3张背 面朝上的卡片中任意摸出一张卡片． （1）请你用列表或画树状图的方法，表示出所有可能出 现的结果； （2）小红和小莉做游戏，制定了两个游戏规则： 规则1：若两次摸出的数字，至少有一次是“6”，小红 赢；否则，小莉赢． 规则2：若摸出的卡片上的数字是球上数字的整数倍时， 小红赢；否则，小莉赢． 小红要想在游戏中获胜，她会选择哪一种规则，并说明 理由．
6. （2012贵州黔南10分）市“消费者协会”联合市 工商局在某中学分别开展打击“地沟油”及“瘦肉精” 的食品宣传讲座，小青同学不知该如何听课，最后他 决定通过掷硬币来确定，掷硬币规则如下：连续抛掷 硬币三次，如果三次正面朝上或三次反面朝上，则小 青听两堂讲座；如果两次正面朝上一次反面朝上，则 小青去听有关“地沟油”的讲座；如果两次反面朝上 一次正面朝上，则小青去听有关“瘦肉精”的讲座。 （1）用画树状图的方法表示三次抛掷硬币的所有结 果； （2）小青听两堂知识讲座的概率有多大？ （3）小青用这个游戏规则去选择听“地沟油”或 “瘦肉精”的讲座是否合理？为什么？

蒲丰投针实验原理1.地球是一个球体：在蒲丰时代，人们普遍相信地球是一个球体，而蒲丰的实验就是为了验证这一点。

2.光线传播是直线传播：蒲丰认为光线传播是呈直线传播的，这是基于他对光学的观察和实验中得到的结论。

基于以上前提，蒲丰提出了以下实验步骤来验证地球的球形：1.准备一个平坦的地面：选择一个平坦的地面，比如一块大理石板或者是一个平整的木板。

2.准备一把针：选择一根细长的针，尽量确保它是笔直的。

3.垂直投放针：将针垂直地向地面投放，确保它垂直于地面，并且尽量避免针倾斜或弯曲。

4.观察针在地面上的分布：观察针在地面上的分布情况，看是否存在一定的规律。

理论上，如果地球是一个平坦的平面，那么无论针的位置如何投放，针都应该均匀地分布在地面上。

然而，如果地球是一个球体，那么针的位置投放将会影响其在地面上的分布。

由于地球表面的曲率，针的投放位置不同将导致一些规律的变化。

根据蒲丰的实验，当针被随机分布在地面上时，如果地球是一个球体，那么在一些特定范围内的细长物体的位置分布将会有所偏差。

这是因为在投针的过程中，总有一些针会与地面相交，而一些则不会。

蒲丰实验的原理是基于概率统计的方法。

通过计算和观察一系列接触和不接触地面的针，可以推导出地球的曲率和球形。

如果这些数据和理论上的期望一致，那么可以得出结论地球是球状的。

总结起来，蒲丰投针实验的原理是基于光线的直线传播以及地球的球形假设。

通过观察针在地面上的分布情况，可以验证地球是否是球状的。

这个实验的重要性在于它提供了一种简单直观的方法来验证古代关于地球形状的理论，并且可以通过实验数据来验证理论的正确性。