西安交大电信学院自动化2014考研真题回忆版811自控与信号与系统

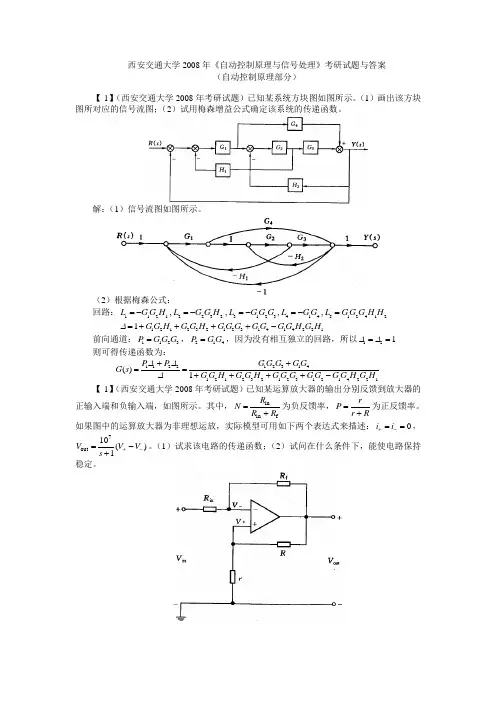
西安交通大学2008年《自动控制原理与信号处理》考研试题与答案（自动控制原理部分）【-1】（西安交通大学2008年考研试题）已知某系统方块图如图所示。

（1）画出该方块图所对应的信号流图；（2）试用梅森增益公式确定该系统的传递函数。

解：（1）信号流图如图所示。

（2）根据梅森公式：回路：1121L G G H =-,2232L G G H =-,3123L G G G =-,414L G G =-,512412L G G G H H =12123212314142211G G H G G H G G G G G G G H G H ∆=++++-前向通道：1123P G G G =，214P G G =，因为没有相互独立的回路，所以121∆∆== 则可得传递函数为：1231411221212321231214221()1G G G G G P P G s G G H G G H G G G G G G G H G H ∆∆∆++==++++- 【-1】（西安交通大学2008年考研试题）已知某运算放大器的输出分别反馈到放大器的正输入端和负输入端，如图所示。

其中，in in f R N R R =+为负反馈率，rP r R=+为正反馈率。

如果图中的运算放大器为非理想运放，实际模型可用如下两个表达式来描述：0i i +-==，7out 10()1V V V s +-=-+。

（1）试求该电路的传递函数；（2）试问在什么条件下，能使电路保持稳定。

解：（1）因为0i -=，所以：outin in f V V V V R R ----=① 同理，因为0i +=，所以： out V V V R r ++-=② 由①式，得： in in out f (1)RV N V V R -⎛⎫=-+ ⎪⎝⎭③由②式，得： out out rV V P V R r+==⋅+ ④ 将7out10()1V V V s +-=-+代入式③和④式，可得： 77out 77in (1)10(1)10()10(1)1()10V N N V P N s s N P -⨯-⨯==-⨯-+++-⨯ （2）当闭环极点位于左半s 平面时，系统稳定。

西安电子科技大学 通信工程学院 考研专业课 ③ 811历年考研真题2012年·第1页西 安 电 子 科 技 大 学2012年攻读硕士学位研究生入学考试试题考试科目代码及名称 811 信号与系统、通信原理 考 试 时 间 2012年 1 月 8 日下午（３小时）答题要求：所有答案（选择题、填空题按照题号写）必须写在答题纸上，写在试题上一律作废，准考证号写在指定位置！！第一部分 通信原理（总分75分）一、填空题（共10题，每题1分，共10分）1.某二进制信源输出0和1代码（等概出现且相互独立），若对输出的代码序列进行AMI 编码，则编码后的序列中代码0所包含的信息量为__________。

2.均值为0，方差为2σ的两个相互独立的高斯随机变量1n ，2n ，通过线性变换后得到随机变量：12x an bn =-（a 和b 均为常数），则x 的概率密度为__________。

3.某电离层反射信道的最大多径时延差为0.5ms ，为避免频率选择性衰落，工程上认为在该信道上传输线性已调数字信号的码元速率不应超过__________波特。

4.在调频广播中，音频的最高频率为15kHz ，最大频偏为75kHz ，则调频广播发射信号的带宽为__________。

5.若二进制基带信号中，0和1出现的概率分别为1P 和2P ，则其对应的基带信号基本波形1()g t 和2()g t 满足__________条件时，基带信号无离散谱。

6.在多相（MPSK ）系统中，随着M 的增加所带来的好处与代价是__________。

7.功率受限于S ，信道中噪声的功率谱密度为0n ，带宽不受限的条件下，系统的信道容量为__________。

8.PCM30/32路基群的比特率为__________。

9.码组0101100的码重为__________，它与码组00111110之间的码距为__________。

（此题出错，两个码组的长度应该是一样的，请将第二个码组去掉一个1。

目　录
第一部分　南昌大学811信号与系统考研真题
2009年南昌大学811电子线路、信号与系统考研真题2008年南昌大学电路、信号与系统考研真题
2007年南昌大学810电路、信号与系统考研真题2006年南昌大学电路、信号与系统考研真题
2005年南昌大学电路、信号与系统考研真题
2004年南昌大学电路信号与系统考研真题
第二部分　兄弟院校数字电路考研真题
2015年华南理工大学824信号与系统考研真题
2014年重庆大学841信号与系统考研真题
2014年武汉大学936信号与系统考研真题
2014年北京邮电大学信号与系统考研真题
第一部分　南昌大学811信号与系统考研真
题
2009年南昌大学811电子线路、信号与系统考研真题
2008年南昌大学电路、信号与系统考研真题
2007年南昌大学810电路、信号与系统考研真题
2006年南昌大学电路、信号与系统考研真题
2005年南昌大学电路、信号与系统考研真题。

习题一1.1绘出下列信号的波形图(1) ；(2) ；(3) ；(4)(5) ;(6) ;(7) ;(8) ;(9) ;(10) , 式中。

1.2 绘出下列信号的图形(1) ;(2) ;(3) ;(4) ;(5) ;(6) ;(7) ;(8) 。

1.3 试写出题图1.1各信号的解析表达式题图1.11.4 判定下列信号是否为周期信号。

若是周期信号，则确定信号周期T。

(1) ;(2) ;(3) ;(4) ;(5) ;(6) ;(7) ;(8) 。

1.5 已知连续时间信号x (t)和y (t)分别如题图1.2 (a)、(b)所示，试画出下列各信号的波形图。

(1) ; (2) ;(3) ; (4) ;(5) ; (6) ;(7) ; (8) ;(9) ; (10) ;(11) ; (12) 。

题图 1 .21.6 已知离散时间信号x (k)和y (k)分别如图1.3 (a)、（b）所示，试画出下列序列的图形：(1) ; (2) ;(3) ; (4) ;(5) ；（6）；（7）；（8）。

题图1.3题图1.41.7 已知信号x (t)、y (t)的波形如题图1.2 所示，分别画出和的波形。

1.8 已知信号f (t+1)的波形如题图1.4 所示，试画出的波形。

1.9 分别画出题图 1.3中信号x (k)、y (k)的、一阶前向差分、一阶后向差分和迭分。

1.10 画出下列各信号的波形：(1) ; (2) ;(3) ; (4) 。

1.11 计算下列各题。

(1) ; (2) ;(3) ; (4) ;(5); (6) :(7) ; (8) ;(9) ; (10) 。

1.12 如图1.5所示电路，输入为，分别写出，以、为输出时电路的输入方程。

1.13 如题图1.6所示电路，输入为，分别写出以、为输出时电路的输入输出方程。

1.14 设某地区人口的正常出生率和死亡率分别为，第k年从外地迁入的人口为f (k)。

若令该地区第k年的人口为y (k)，写出y (k)的差分方程。

西 安 邮 电 学 院2014年招收攻读硕士学位研究生入学考试试题 考试科目代码及名称 824信号与系统A注：符号()t ε为单位阶跃函数，()k ε为单位阶跃序列，LTI 为线性时不变。

一、填空题（每空3分，共30分）1．积分102312d 2t e t t δ--⎛⎫--= ⎪⎝⎭⎰2．已知()(1)(2)h t t t εε=---，()(2)(4)f t t t εε=---，则卷积()()h t f t *=3．已知一离散LTI 系统的阶跃响应1()()2kg k k ε⎛⎫= ⎪⎝⎭，则该系统的单位序列响应()h k = 4．已知信号()f t 的波形如右图所示， 其傅里叶变换记为()F j ω，试求()d F j ωω∞-∞=⎰0(0)()F F j ωω===5．因果信号()f t 的单边拉普拉斯变换为()221()1s s e F s s --=+，则对应原函数的初值(0)f += ，终值()f ∞= 6．已知一连续系统的零、极点分布如右图 所示，()1H ∞=，则系统的系统函数 ()H s =7．对信号()()f t Sa t =进行均匀抽样的奈奎斯特抽样间隔s T =-28. 双边Z变换的象函数23()1132zF zz z，收敛域为1132z，则其对应的原序列()f k二、选择题（共10题，每题4分，共30分）1．周期序列3()cos cos4436f k k kππππ，其周期为（）（A）8 （B）16 （C）24（D）482. 序列和2(2)kiiiδ等于（）（A）4 （B）1 （C）4()kε（D）4(2)kε3. 信号()()tf t e tε的傅里叶变换()F jω等于（）（A）11jω（B）11jω（C）11jω（D）11jω4. 如下图所示周期信号()f t，该信号不可能含有的频率分量是（）（A）0.5Hz（B）1Hz（C）1.5Hz （D）2.5Hz5. 一个线性时不变的连续时间系统，其在某激励信号作用下的自由响应为3()t te e tε，强迫响应为21()te tε，则下面的说法正确的是（）（A）该系统一定是二阶系统；（B）该系统一定是稳定系统；（C ）零输入响应中一定包含3()tte e t ε；（D ）零状态响应中一定包含21()tet ε。

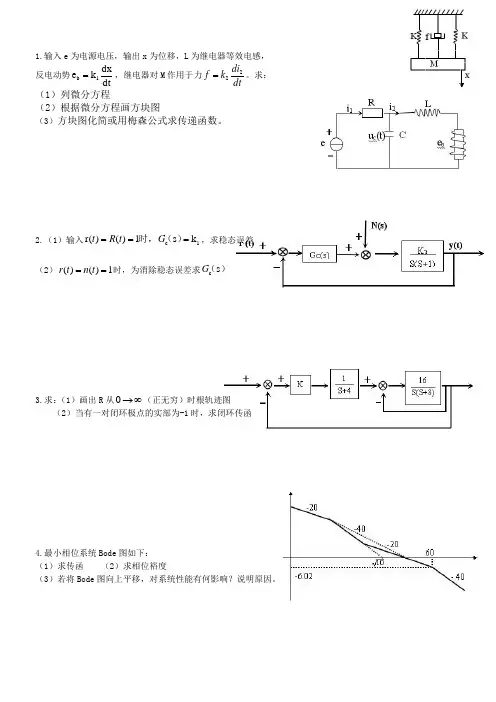
1.输入e 为电源电压，输出x 为位移，L 为继电器等效电感， 反电动势dt dx k e 1b =，继电器对M 作用于力dtdi k f 22=。

求： （1）列微分方程（2）根据微分方程画方块图（3）方块图化简或用梅森公式求传递函数。

2.（1）输入1c k s 1)()(r ===）（时，G t R t ，求稳态误差 （2）1)()(==t n t r 时，为消除稳态误差求）（s c G3.求：（1）画出R 从∞→0（正无穷）时根轨迹图（2）当有一对闭环极点的实部为-1时，求闭环传函4.最小相位系统Bode 图如下：（1）求传函 （2）求相位裕度（3）若将Bode 图向上平移，对系统性能有何影响？说明原因。

5.n 阶系统有p 个极点在左平面（p<n ）,奈奎斯特路径如图，+∞→=0,从w jw s 232,,Re s ππθθ→+∞→=从R j 0,→∞-=从w jw s则：（1）奈奎斯特稳定判据如何表述？（2）若含积分积分环节，则奈奎斯特路径如何选取？《信号与系统》6.)1()()(--=t u t u t x )3()1(u 2)(t h -+--=t u t t u ）（ )h *t )(t x t y （）（=用图解法求y(t)7.求)(]cos [)(02t u t w et x t -=的拉普拉斯变换X （s ），并指出ROC8.不记得9.用长除法求出211)211(1z (----=z z X ）的反变换前5项，写成：+-+-+-+-+-+=)5()5()4()4()3()3()2()2()1()1()()0()(n x n x n x n x n x n x n x δδδδδδ形式。

10.（1）求P （t ）的傅里叶系数及拉氏变化）（jw p X（2）不记得（图没画完整）（注：素材和资料部分来自网络，供参考。

请预览后才下载，期待你的好评与关注！）。