2 同时决策博弈(2)
- 格式:pdf
- 大小:206.56 KB
- 文档页数:40

第17章决策与博弈论17.1 复习笔记1.博弈论的基本概念(1)博弈及其三个要素博弈论是在一个简化的体系里描述复杂的决策问题,这些决策问题往往涉及多个行为者,他们之间的决策相互依存,相互作用。
博弈包含三个要素:①参与者;②决策;③报酬。
(2)合作与非合作博弈如果在博弈参与者之间可形成共同计划的决策这类具有约束性的合同,那么这类博弈被称为合作性的博弈。
如果在参与者之间不能达成或实施有约束性的合同,这类博弈则被称作非合作性的博弈。
(3)主导策略(占优策略均衡)主导策略是指对某参与者而言,不管其竞争对手的反应如何,这一决策总是最优的策略。
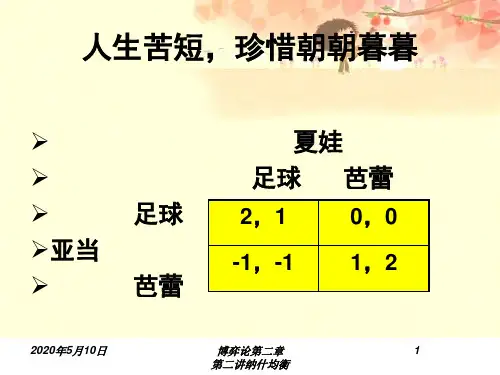
2. 纳什均衡(1)纳什均衡纳什均衡是指在给定对方行动的前提下可以给每个参与者都带来最佳结果的某种决策(或行动)。
达到纳什均衡时,每一个博弈者都确信,在给定竞争对手策略决定的情况下,他选择了最好的策略。
也就是说,给定其他人的战略,任何个人都没有积极性去选择其他战略,从而这个均衡没有人有积极性去打破。
占优策略均衡即是一种纳什均衡。
占优策略均衡若存在,只存在惟一均衡,而纳什均衡可能存在多重解。
(2)最大极小决策(囚徒困境)最大极小决策反映的是,从个人角度出发所选择的占优策略,从整体来看,却是最差的结局,即个人理性与团体理性的冲突。
这一决策可以发生在不少的博弈场合,也可以解释卡特尔联盟的不稳定性。
(3)混合策略在有些博弈中,仅采取一种决策或一种行动的“纯决策”不是最好的决策,即可能不存在纳什均衡。
而以某特定的概率P选择一种行为,以1-P的概率选择另一种行为,则有可能是纳什均衡的解。
这时的选择被称为混合策略。
但反过来需要注意,存在混合策略均衡的博弈也有可能存在非混合策略的均衡。
3. 重复博弈重复博弈即同一个博弈被重复多次的动态博弈,它是反复不断进行的。
在无限期重复博弈中,对于任何一个参与者的欺骗和违约行为,其他参与者总会有机会给予报复。
所以,每一个参与者都不会采取违约或欺骗的行为,囚犯困境合作的均衡解是存在的。

1.设一四阶段两博弈方之间的动态博弈如图所示。
试找出全部子博弈,讨论该博弈中的可信性问题,求子博弈完美纳什均衡策略组合和博弈的结果。
2.假设一个工会是一个寡头垄断市场中所有企业唯一的劳动力供给者,就像汽车工人联合会对于通用、福特、克莱斯勒等大的汽车厂家。
令博弈各方行动的时间顺序如下:(1)工会确定单一的工资要求w ,适用于所有的企业(2)每家企业i 了解到w ,然后同时分别选择各自的雇佣水平L i ;(3)工会的收益为(w-w α)L ,其中w α为工会成员到另外的行业谋职可取得的收入,L=L 1+…L n 为工会在本行业企业的总就业水平;企业i 的利润为π(w ,L i ),其中决定企业i 利润水ABB A h g (2,4)(8,5)(3,6)(4,3)b (5,3)a c d f e平的要素如下。
所有企业都有同样的生产函数:产出等于劳动力q i=L i。
市场总产出为Q=q1+…+q n时的市场出清价格为p(Q)=a-Q。
为使问题简化,假设企业除了工资支出外没有另外的资本。
求出此博弈的子博弈精炼解。
在子博弈精炼解中,企业的数量是如何影响工会的效应的?为什么?(吉本斯2.2节 2.7答案)3.下图所示的同时行动博弈重复进行两次,并且第二阶段开始前双方可观测到第一阶段的结果,不考虑贴现因素。
变量x大于4,因而(4,4)在一次性博弈中并不是一个均衡收益。
对什么样的x,(双方参与者同时采取)下述战略是一个子博弈完美纳什均衡?第一阶段选择Q i,如果第一阶段的结果为(Q1,Q2),在第二阶段选择P i;如果第一阶段的结果为(y,Q2),其中y≠Q1,第二阶段选择R i;如果第一阶段的结果为(Q1,z),其中z≠Q1,第二阶段选择S i;如果第一阶段结果为(y,z),其中y≠Q1,且z≠Q2,则在第二阶段选P iP2 Q2 R2 S2P1Q1R1S1(2.10吉本斯)思路:逐个分析上述的四种情形:第一种情形,第一阶段选择Qi,第二阶段选择Pi,即双方均采取合作的策略,得益均为6;第二种情形和第三种情形下,实际上有一方是采取了不合作,其得益为x,另一方即利益受损方得益为2;第四种情形实际上是双方都不采取合作的策略,而根据题目要求,对于x,下述战略是一个子博弈精炼纳什均衡,所以x必须小于双方均合作时的收益6,否则第一种情形不会出现,因为既然x>6了,双方均会选择不合作而使情形一不会出现。


管理决策博弈法计算题(最新版)目录1.管理决策博弈法简介2.管理决策博弈法计算题的类型3.管理决策博弈法计算题的解法4.管理决策博弈法计算题的应用实例5.总结正文【1.管理决策博弈法简介】管理决策博弈法是一种用于解决管理决策问题的数学方法,它基于博弈论,通过分析决策者之间的相互作用,研究决策者的策略选择和决策结果。
管理决策博弈法可以帮助决策者在复杂的决策环境中找到最佳的决策策略,从而实现组织目标。
【2.管理决策博弈法计算题的类型】管理决策博弈法计算题主要包括以下几种类型:(1)静态博弈计算题:静态博弈是指在一次性决策中,决策者需要同时做出决策,并且每个决策者的决策不会受到其他决策者的影响。
(2)动态博弈计算题:动态博弈是指在多次性决策中,决策者需要根据其他决策者的决策结果,调整自己的决策策略。
(3)完全信息博弈计算题:完全信息博弈是指决策者拥有完全的信息,可以准确地预测其他决策者的决策结果。
(4)不完全信息博弈计算题:不完全信息博弈是指决策者拥有不完全的信息,无法准确地预测其他决策者的决策结果。
【3.管理决策博弈法计算题的解法】管理决策博弈法计算题的解法主要包括以下几种:(1)纳什讨价还价解法:纳什讨价还价解法是一种用于解决静态博弈问题的方法,它假设每个决策者都会选择最优的策略,并且每个策略都会考虑到其他决策者的可能策略。
(2)重复博弈解法:重复博弈解法是一种用于解决动态博弈问题的方法,它假设决策者会在多次决策中,根据其他决策者的决策结果,调整自己的策略。
(3)贝叶斯博弈解法:贝叶斯博弈解法是一种用于解决不完全信息博弈问题的方法,它假设决策者会根据自己拥有的信息,对其他决策者的策略进行概率分析,并选择最优的策略。
【4.管理决策博弈法计算题的应用实例】管理决策博弈法计算题在实际应用中,可以解决许多管理决策问题,例如:(1)定价决策:在市场竞争中,企业需要根据竞争对手的价格策略,选择最佳的定价策略。


博弈论课程设计1、引言博弈论是现代数学中的一个重要分支,是由经济学家和数学家共同合作发展起来的。
博弈论主要研究人类社会中的决策行为和相互关系,以及在涉及决策行为和相互关系的情景中个体或组织如何做出理性的决策。
博弈论在生物学、心理学、社会学、管理学、工程学等领域也有广泛的应用。
在博弈论的学习过程中,理论与实践相结合是必不可少的。
本文将介绍一些博弈论的课程设计,旨在帮助学生更好地理解和应用博弈论的知识。
2、课程设计2.1 美国拍卖模拟实验美国拍卖是一种竞价拍卖。
在竞拍过程中,买家通过不断提高他们的出价来争夺商品,最后出价最高者获得商品所有权。
美国拍卖的特点是出价者可以随时根据拍卖过程中的信息改变他们的出价。
该模拟实验的目的是通过竞卖过程的模拟来让学生学习博弈论中的核心概念,如策略、博弈纳什均衡等。
该实验还可以帮助学生分析竞价策略与结果的关系,提高学生思考和策略制定的能力。
2.2 博弈纳什均衡实验博弈纳什均衡是博弈论中的一个重要概念。
在一个博弈中,如果所有参与者都选择了他们各自的最优策略,那么这个博弈就到达了一个均衡状态,称为纳什均衡。
该实验可以让学生自己尝试找到博弈的纳什均衡,提高学生的逻辑推理和自主思考能力。
同时,这个实验中涉及到的博弈模型也可以用来分析和解决现实生活中的问题。
2.3 连续混合策略实验连续混合策略是博弈论中的一个重要概念,它在实际应用中有广泛的应用。
在连续混合策略中,玩家有一个概率分布,他们可以随机选择他们的行动。
在竞争和合作的情况下,连续混合策略被用来描述下注、选择行为模型等。
在本实验中,学生将学习如何制定连续混合策略并评估它们的效果。
通过该实验,学生将加深对复杂博弈策略的理解和应用,提高学生的计算能力和分析能力。
3、结语博弈论不仅仅是一种专业的数学知识,它已经成为了理解和解决社会问题的一种重要的工具。
实践是理论的检验,课程设计可以帮助学生更好地理解和应用博弈论的知识。
希望本文介绍的三个课程设计能够为读者提供一些启示,帮助读者更好地理解博弈论的知识和应用。




博弈论讲义——完全信息静态博弈❑❑❑博弈❑论讲义——完全信息静态博弈博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈论讲义——完全信息静态博弈博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑r1博弈论讲义——完全信息静态博弈r1博弈论讲义——完全信息静态博弈r1博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈3/4博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈博弈论讲义——完全信息A 静态博弈博弈论讲义——完全信息A 静态博弈博弈论讲义——完全信息静态博弈❑❑博弈论讲义——完全信息静态博弈❑❑博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑上述问题可表示为双矩阵形式,见图❑该博弈也存在两个纯策略纳什均衡,分别为❑博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈❑❑博弈论讲义——完全信息静态博弈❑❑博弈❑论讲义——完全信息静态博弈博弈论讲义——完全信息静态博弈D U参与人1博弈论讲义——完全信息静态博弈D U参与人1博弈论讲义——完全信息静态博弈D U参与人1博弈论讲义——完全信息静态博弈参与人1博弈论讲义——完全信息静态博弈博弈❑论讲义——完全信息静态博弈。
博弈论贝叶斯纳什均衡一、引言博弈论是研究决策者在相互影响中做出决策的科学。
贝叶斯纳什均衡是博弈论中的一种解法,它考虑了不完全信息下的决策问题,被广泛应用于经济学、政治学、计算机科学等领域。
本文将从博弈论和贝叶斯纳什均衡两个方面进行详细介绍。
二、博弈论1.基本概念博弈论中有三个基本概念:玩家、策略和收益。
玩家是参与游戏的实体,可以是个人、组织或国家等。
每个玩家都有自己的目标和利益。
策略是指玩家在游戏中做出的选择。
每个玩家都有多种可选的策略,每种策略都对应着不同的收益。
收益是指每个玩家在游戏结束后获得的利益或损失。
收益可以用数字表示,也可以用其他方式来描述。
2.分类根据游戏参与者数量和信息情况,博弈论可以分为以下几类:(1)单人博弈:只有一个玩家参与游戏,如囚徒困境。
(2)双人博弈:有两个玩家参与游戏,如零和博弈、非零和博弈等。
(3)多人博弈:有多个玩家参与游戏,如合作博弈、竞争博弈等。
(4)完全信息博弈:每个玩家都知道其他玩家的策略和收益情况,如国际象棋。
(5)不完全信息博弈:每个玩家只知道自己的策略和收益情况,不知道其他玩家的策略和收益情况,如扑克牌。
3.解法解决一个博弈问题需要找到一种最优的策略组合,使得每个玩家都能够获得最大化的收益。
常见的解法有纳什均衡、帕累托最优解等。
三、贝叶斯纳什均衡1.基本概念贝叶斯纳什均衡是指在不完全信息下的多人博弈中,每个玩家根据已知信息做出最优选择所形成的策略组合。
它包含两个部分:先验概率和后验概率。
先验概率是指每个玩家在游戏开始前对其他玩家的策略和收益情况所做的预测。
后验概率是指每个玩家在游戏进行过程中,根据已知信息对其他玩家的策略和收益情况所做的修正。
2.求解方法贝叶斯纳什均衡的求解方法可以分为两种:直接求解和迭代求解。
直接求解是指通过计算每个玩家在不同信息情况下的期望收益,找到满足条件的最优策略组合。
这种方法适用于信息量较少、博弈参与者较少的情况。
迭代求解是指通过反复修正先验概率和后验概率,最终找到满足条件的最优策略组合。