应用光学知识点
- 格式:doc
- 大小:457.50 KB
- 文档页数:9
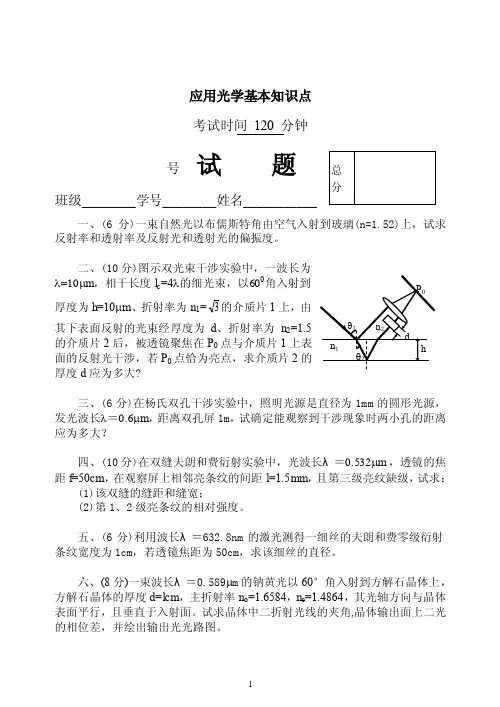
应用光学基本知识点 考试时间 120 分钟号试 题班级________学号________姓名___________一、(6分)一束自然光以布儒斯特角由空气入射到玻璃(n=1.52)上,试求反射率和透射率及反射光和透射光的偏振度。
二、(10分)图示双光束干涉实验中,一波长为 λ=10μm ,相干长度l c =4λ的细光束,以600角入射到 厚度为h=10μm 、折射率为n 1=3的介质片1上,由其下表面反射的光束经厚度为d 、折射率为n 2=1.5的介质片2后,被透镜聚焦在P 0点与介质片1上表面的反射光干涉,若P 0点恰为亮点,求介质片2的厚度d 应为多大?三、(6分)在杨氏双孔干涉实验中,照明光源是直径为1mm 的圆形光源,发光波长λ=0.6μm ,距离双孔屏1m ,试确定能观察到干涉现象时两小孔的距离应为多大?四、(10分)在双缝夫朗和费衍射实验中,光波长λ=0.532μm ,透镜的焦距f=50cm ,在观察屏上相邻亮条纹的间距l=1.5mm ,且第三级亮纹缺级,试求:(1)该双缝的缝距和缝宽;(2)第1、2级亮条纹的相对强度。
五、(6分)利用波长λ=632.8nm 的激光测得一细丝的夫朗和费零级衍射条纹宽度为1cm ,若透镜焦距为50cm ,求该细丝的直径。
六、(8分)一束波长λ=0.589μm 的钠黄光以60°角入射到方解石晶体上,方解石晶体的厚度d=lcm ,主折射率n o =1.6584,n e =1.4864,其光轴方向与晶体表面平行,且垂直于入射面。
试求晶体中二折射光线的夹角,晶体输出面上二光的相位差,并绘出输出光光路图。
总分七、(10分)如图所示,一入射线偏振光的振动方向与晶片光轴方向的夹角为 =26.57°,试问该光经过厚度为0.081mm 的晶片后,其偏振状态如何?(入射光波长λ=589.3nm ,n o =1.5442,n e =1.5533)八、(10分)图示A 为纵向运用的电光晶体KD P (n o =1.512,γ63=10.6×10-10cm/V ),B 为厚度d =10mm的方解石晶体(n o =1.5246,n e =1.4792,光轴方向与通光面的法线方向成45°夹角),A 、B 晶体平行放置。






第一章 几何光学的基本定律§ 1-1 发光点、波面、光线、光束 返回本章要点 发光点 ---- 本身发光或被照明的物点。
既无大小又无体积但能辐射能量的几何点。
对于光学系统来说, 把一个物体看成由许多物点组成,把这些物点都看成几何点 ( 发光点 ) 。
把不论多大的物体均看作许多 几何点组成。
研究每一个几何点的成像。
进而得到物体的成像规律。
当然这种点是不存在的,是简化了的概念。
一个实际的光源总有一定大小才能携带能量,但在计算时,一 个光源按其大小与作用距离相比很小便可认为是几何点。
今后如需回到光的本质的讨论将特别指出。
波面 --- 发光点在某一时刻发出的光形成波面 如果周围是各向同性均匀介质,将形成以发光点为中心的球面波或平面波 第二章 球面和球面系统§ 2-1 什么是球面系统?由球面组成的系统称为球面系统。
包括折射球面和反射球面反射面:n ' =-n.平面是半径为无穷大的球面,故讨论球面系统具有普遍意义折射系统折反系统§ 2-2 概念与符号规则•概念① 子午平面 —— 包含光轴的平面② 截距:物方截距 —— 物方光线与光轴的交点到顶点的距离像方截距 —— 像方光线与光轴的交点到顶点的距离③ 倾斜角:物方倾斜角 —— 物方光线与光轴的夹角像方倾斜角 —— 像方光线与光轴的夹角返回本章要点•符号规则返回本章要点因为分界面有左右、球面有凹凸、交点可能在光轴上或下,为使推导的公式具有普遍性,参量具有确切意 义,规定下列规则:a. 光线传播方向:从左向右b. 线段:沿轴线段 ( L,L',r ) 以顶点 O 为基准,左“ - ”右“ + ” 垂轴线段 ( h ) 以光轴为准,上“ + ”下“ - ” 间隔 d(O1O2) 以前一个面为基准,左“ - ”右“ + ” c. 角度:光轴与光线组成角度 ( U,U' ) 以光轴为起始边,以锐角方向转到光线,顺时针“ + ”逆时针“ - ”光线与法线组成角度 ( I,I' ) 以光线为起始边,以锐角方向转到法线,顺“ + ”逆“ - ”光轴与法线组成角度 ( φ ) 以光轴为起始边,以锐角方向转到法线,顺“ + ”逆“ - ”§ 2-3 折射球面返回本章要点•由折射球面的入射光线求出射光线已知: r, n, n',L, U 求: L', U',由 以上几个公式可得出 L' 是 U 的 函数这一结论, 不同 U 的光线经 折射后不能相交于一点点-》斑,不完善成像•近轴光线经折射球面折射并成像.1 .近轴光线:与光轴很靠近的光线,即 -U 很小 , sin(-U) ≈ -U ,此时用小写:sin(-U)= - usinI=iL=l 返回本章要点近轴光线所在的区域叫近轴区2 .对近轴光,已知入射光线求折射球面的出射光线:即由 l , u —> l ',u' , 以上公式组变为:当 u 改变时, l ' 不变!点 —— 》点,完善成像 此时 A , A' 互为物像,称共轭点近轴光所成像称为高斯像,仅考虑近轴光的光学叫高斯光学返回本章要点近轴光线经折射球面计算的其他形式(为计算方便,根据不同情况可使用不同公式)利用:可导出返回本章要点4 .(近轴区)折射球面的光焦度,焦点和焦距可见,当( n'-n )/r 一定时, l ' 仅与 l 有关。

基础知识1.1924年,德布罗意大胆地创立了物质波动学说。
光既具有粒子性,又具有波动性,光在传播时表现为波动性,而与物质作用时又表现为粒子性。
2.波动光学理论认为,光是某波段的电磁波。
3.可见光的波长范围约为380~760nm4.光源间指性能够辐射光能的物体称为光源。
5.光源可分为普通光源和激光光源。
6.自发辐射有两个特点:其一是随机性其二是间歇性7.具有单一频率的光称为单色光8.由各种频率复合的光称为复色光9.各种不同频率的光将按不同的折射角分开,形成光谱,这种现象称为色散。
10.满足光的相干条件:频率相同的两光波在相遇点有相同的振动方向和恒定的相位差。
满足本条件的光称为相干光11.能发出相干光的光源称为相干光源12.波的叠加原理:从几个波源产生的波在同一介质中传播时,无论它们相遇与否,都保持自己原有的特性,即频率不变、波长不变、振动方向不变,各列波都按自己原来传播的方向继续前进,不受其他波的影响13.折射率和几何路程的乘积,叫做光程14.光程之差称为光程差15.托马斯·杨解释了干涉现象16.光从光疏媒质(折射率小)向光密媒质(折射率大)表面入射时,反射光的位相改变π.它相当于光多(或少)传播半个波长的距离,这种现象称为半波损失17.劳埃德镜实验显示了光的干涉现象,证实了光的波动性,证明了光由光疏介质射向光密介质表面发生反射时,反射光会发生半波损失。
18.相干光,在相遇时将会产生干涉现象,称为薄膜干涉19.光波绕过障碍物的边缘传播的现象叫做光的衍射20.衍射系统由光源、衍射屏(障碍物)和接收屏幕(观察屏)组成21.衍射现象分为两类:一类是菲涅耳衍射(距离有限)另一类是夫琅禾费衍射(距离无限远)22.用半波带法分析单缝衍射23.艾里斑的光强占整个衍射光强的约84%24.圆孔愈小或波长愈长,所得艾里斑也越大,衍射现象越明显25.任何具有空间周期性的衍射屏都可以叫做衍射光栅26.光的偏振现象证实了光的横波性质27.自然光与偏振光光波是一种电磁波28.光波是横波,具有偏振特性29马吕斯发现了光的偏振现象30.在所有可能的方向上的光矢量的振动次数和振幅的时间平均值相等,这样的光称为自然光31.这种光振动矢量只在某一平面内沿某一确定方向振动的光,称为平面偏振光亦称为线偏振光32.光的双折射当一束光线在各向同性介质的表面折射时,折射光线只有一束,且遵守折射定律。

第一章几何光学基本定律与成像概念1、波面:某一时刻其振动位相相同的点所构成的等相位面成为波阵面,简称波面。
光的传播即为光波波阵面的传播。
2、光束:与波面对应的所有光线的集合。
3、波面分类:a)平面波:对应相互平行的光线束(平行光束)b)球面波:对应相较于球面波球心的光束(同心光束)c)非球面波4、全反射发生条件:a)光线从光密介质向光疏介质入射b)入射角大于临界角5、光程:光在介质中传播的几何路程l与所在介质的折射率n的乘积s。
光程等于同一时间内光在真空中所走的几何路程。
6、费马原理:光从一点传播到另一点,期间无论经过多少次折射和反射,其光程为极值。
7、马吕斯定律:光线束在各向同性的均匀介质中传播时,始终保持着与波面的正交性,并且入射波面与出射波面对应点之间的光程均为定值.8、完善像:a)一个被照明物体每个物点发出一个球面波,如果该球面波经过光学系统后仍为一球面波,那么对应光束仍为同心光束,则称该同心光束的中心为物点经过光学系统后的完善像点.b)每个物点的完善像点的集合就是完善像。
c)物体所在空间称为物空间,像所在空间称为像空间。
10、完善成像条件:a)入射波面为球面波时,出射波面也为球面波。
b)或入射光为同心光束时,出射光也为同心光束。
c)或物点A1及其像点之间任意两条光路的光程相等.11、物像虚实:几个光学系统组合在一起时,前一系统形成的虚像应看成当前系统的实物。
12、子午面:物点和光轴的截面.13、决定光线位置的两个参量:a)物方截距:曲面顶点到光线与光轴交点A的距离,用L表示。
b)物方孔径角:入射光线与光轴的夹角,用U表示。
14、符号规则a)沿轴线段:以折射面顶点为原点,由顶点到光线与光轴交点或球心的方向于光线传播方向相同时取证,相反取负b)垂轴线段:以光轴为基准,在光轴上方为正,下方为负。
c)夹角:i.优先级:光轴》光线》法线。
ii.由优先级高的以锐角方向转向优先级低的。
iii.顺时针为正,逆时针为负。
《应用光学》总复习提纲第一章★1、光的反射定律、折射定律I1 = R1;n1sinI1=n2sinI22、绝对折射率介质对真空的折射率。
通常把空气的绝对折射率取作1,而把介质对空气的折射率作为“绝对折射率”。
★3、光路可逆定理假定某一条光线,沿着一定的路线,由A传播到B。
反过来,如果在B点沿着相反的方向投射一条光线,则此反向光线仍沿原路返回,从B传播到A。
★4、全反射光线入射到两种介质的分界面时,通常都会发生折射与反射。
但在一定条件下,入射到介质上的光会全部反射回原来的介质中,没有折射光产生,这种现象称为光的全反射现象。
发生全反射的条件可归结为:(1)光线从光密介质射向光疏介质;(2)入射角大于临界角。
(什么是临界角?)★5、正、负透镜的形状及其作用正透镜:中心比边缘厚度大,起会聚作用。
负透镜:中心比边缘厚度小,起发散作用。
★7、物、像共轭对于某一光学系统来说,某一位置上的物会在一个相应的位置成一个清晰的像,物与像是一一对应的,这种关系称为物与像的共轭。
例1:一束光由玻璃(n=1.5)进入水中(n=l.33),若以45°角入射,试求折射角。
解:n1sinI1=n2sinI2n1=1.5; n2=l.33; I1=45°代入上式得I2=52.6°折射角为52.6°第二章★1、符号规则;2、大L公式和小l公式★3、单个折射球面物像位置公式例:一凹球面反射镜浸没在水中,物在镜前300mm 处,像在镜前90mm 处,求球面反射镜的曲率半径。
n ′l ′-n l=n ′-n r l =-300mm ,l ′=-90mm求得r=-138.46mm由公式解:由于凹球镜浸没在水中,因此有n ′=-n=n 水★4、单个球面物像大小关系例:已知一个光学系统的结构参数:r = 36.48mm ;n=1;n ′=1.5163;l = -240mm ;y=20mm ;可求出:l ′=151.838mm ,求垂轴放大率β与像的大小y ′。
应用光学第一章总结知识点一、基本概念1. 光的本质光是一种电磁波,具有双重性质,既能像波一样传播,又能像粒子一样照射。
2. 光的特性光具有波长、频率、速度和偏振等特性,光的波长决定了它的颜色,频率决定了它的亮度,速度取决于介质的折射率,偏振决定了光的方向性。
3. 光的传播光在真空中的传播速度是光速,而在不同介质中传播的速度和方向都会发生变化。
光的传播遵循光线理论和波动理论。
4. 光的干涉和衍射光的干涉和衍射是光学现象的重要表现形式,它们揭示了光的波动性。
干涉是指两束波相遇时相互干扰的现象,衍射是指波通过孔隙或物体边缘时发生的扩散和弯曲。
5. 光的吸收和发射光与物质相互作用时会发生吸收和发射,物质的吸收和发射特性与光的波长有关。
二、光学元件1. 透镜透镜是光学系统的重要组成部分,它能够折射光线,使光线汇聚或发散。
透镜有凸透镜和凹透镜之分,可以用在光学仪器中进行成像。
2. 镜面镜面是能够反射光线的表面,具有平面镜、球面镜等形式。
镜面的反射特性与入射角和反射角有关,根据镜子的曲率不同,反射出的光线会发生聚焦或发散。
3. 棱镜棱镜是一种类似透镜的光学元件,它能够使光线发生色散,将不同波长的光线分散成不同的方向。
4. 光栅光栅是一种利用周期性的结构使光发生衍射的光学元件,它可以分解光线,用于光谱仪等领域。
5. 波片波片是一种能够改变光线偏振状态的光学元件,常用于偏振光学和激光器件中。
6. 光阑光阑是一种用于控制光线传播的光学元件,它能够限制光线的传播范围,提高光学系统的分辨率。
7. 光学滤波器光学滤波器是一种通过选择性吸收或透射特定波长光线的光学元件,它可以应用于激光器件、摄像头和光学测量中。
8. 光学偏振元件光学偏振元件是一种能够改变光线偏振状态的光学元件,包括偏振片、偏光镜和偏振棱镜等。
三、光学系统1. 成像系统成像系统是由透镜、镜面和光学滤波器等组成,它能够将物体上的信息投影到成像平面上,形成清晰的图像。
光学的有关知识点总结一、光的基本特性光的本质是电磁波,它具有一系列独特的特性:1. 光速恒定:光在真空中的速度是光速,等于30万公里/秒,但在介质中的速度会有所改变。
2. 光的波粒二象性:光既有波动性,也有粒子性,表现为波粒二象性。
3. 光的波长和频率:波长和频率是光的两个基本参数,波长越短,频率越高,能量越大。
4. 光的直线传播:在均匀介质中,光沿直线传播。
5. 光的反射和折射:光与介质交界面产生反射和折射现象。
6. 光的干涉和衍射:光具有干涉和衍射现象,这是光波动性的表现。
二、光学基本原理1. 光的传播:光在真空中是直线传播,但在介质中会产生折射和散射现象。
2. 光的反射和折射:当光射入介质时,会发生反射和折射。
反射是光线与物体表面相交后发生的现象,而折射是光线从一种介质到另一种介质时产生的弯曲现象。
3. 光的焦点和成像:透镜和凸面镜具有成像功能,能够将光线聚焦到一个点上,这个点称为焦点。
通过透镜和凸面镜,可以实现光学成像。
4. 光的干涉和衍射:当两束光线交叠在一起时,会产生干涉现象;当光波通过障碍物后发生偏折时,会产生衍射现象。
三、光学器件1. 透镜:透镜是一种具有成像功能的光学器件,它可以将光线聚焦或发散。
透镜有凸透镜和凹透镜之分,可以用来成像、矫正视力等。
2. 凸面镜:凸面镜也是一种具有成像功能的光学器件,它可以将光线聚焦到一点上,通常用于放大物体、制作望远镜等。
3. 光栅:光栅是一种具有干涉功能的光学器件,它通过光的干涉现象来分离光谱,常用于光谱分析、激光器、光通信等领域。
4. 红外和紫外光学器件:红外和紫外光学器件广泛应用于红外和紫外光学系统中,包括红外夜视仪、红外热像仪、紫外消毒灯等。
5. 其他光学器件:还有偏振片、棱镜等光学器件,它们在光学领域有着重要的应用。
四、光学仪器1. 显微镜:显微镜是一种用来观察微小物体的仪器,它可以放大物体的微小结构,并通过眼镜或相机进行观察和研究。
初中物理光学应用知识点光学是物理学中的一个重要分支,主要研究光的传播、反射、折射、干涉、衍射、偏振等现象。
光学在日常生活中有着广泛的应用,影响着人们的生活和各种科学技术领域。
下面将介绍一些光学的应用知识点。
1.镜子与光学成像镜子是光学的应用中最常见的工具之一、我们常用的平面镜、凸透镜、凹透镜等都能够将光线反射或折射从而形成图像。
镜面反射成像是指通过平面镜,光线的入射角等于反射角,从而形成逆立的虚像。
球面镜反射成像的特点是与球心连线与入射光线的入射角等于反射角。
2.折射与透镜成像当光线在由一种介质射向另一种介质时,会因为折射现象而改变方向。
透明材料如玻璃等可以用来制作透镜,透镜是一种能够通过折射调节光线路径的设备。
凸透镜会使得光线汇聚,而凹透镜会使得光线发散。
基于透镜成像的原理,我们可以制作出望远镜、显微镜、眼镜等设备。
3.光的干涉现象干涉现象是指两束或多束光线相遇时会产生明暗相间的交叉条纹。
干涉现象在日常生活中有着广泛的应用,比如可见光的干涉咖啡特效、反光镜的工作原理等。
我们可以通过调节光路和控制干涉条纹的形态来测量物体的形状、厚度和折射率。
4.光的衍射现象光的衍射现象是指光通过一条缝隙或物体边缘时会发生弯曲和扩散的现象。
利用衍射,我们可以制作出衍射光栅,通过测量衍射条纹的位置和间距来确定光的波长。
此外,光的衍射现象也广泛应用于显微镜、望远镜、激光等技术中。
5.光的偏振现象光波的振动方向决定了光的偏振状态。
光的偏振现象在光学领域和显示技术中有着重要的应用。
比如偏振墨镜可以过滤掉透射光中的一部分,只保留一个方向的振动。
光的偏振现象也广泛应用于液晶显示屏、光学通信等技术中。
6.光学仪器与设备光学仪器与设备包括望远镜、显微镜、光谱仪、激光等。
望远镜可以用来观察远处的天体,显微镜可以放大微观物体的细节。
光谱仪可以将光分解成不同波长的组成,通过分析光谱,我们可以了解物质的组成和性质。
激光是一种具有高度聚焦性、定向性和单色性的光源,广泛应用于医学、通信、材料加工等领域。
应用光学简答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是直线传播定律、独立传播定律、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播。
独立传播定律:不同光源的光在通过介质某点时互不影响。
反射定律:反射光线位于入射面内;反射角等于入射角;折射定律:折射光线位于入射面内;入射角和折射角正弦之比,对两种一定的介质来说,是一个和入射角无关的常数2111sin sin I n I n 。
2、如何区分实物空间、虚物空间以及实像空间和虚像空间?是否可按照空间位置来划分物空间和像空间?答:实物空间:光学系统第一个曲面前的空间。
虚物空间:光学系统第一个曲面后的空间。
实像空间:光学系统最后一个曲面后的空间。
虚像空间:光学系统最后一个曲面前的空间。
物空间和像空间在空间都是可以无限扩展的,不能按照空间进行划分。
3、什么是共轴光学系统、光学系统物空间、像空间?答:光学系统以一条公共轴线通过系统各表面的曲率中心,该轴线称为光轴,这样的系统称为共轴光学系统。
物体所在的空间称为物空间,像所在的空间称为像空间。
4、什么叫理想光学系统?答:在物像空间均为均匀透明介质的条件下,物像空间符合“点对应点、直线对应直线、平面对应平面”的光学系统称为理想光学系统。
5、用近轴光学公式计算的像具有什么实际意义?答:作为衡量实际光学系统成像质量的标准;用它近似表示实际光学系统所成像的位置和大小。
6、 理想光学系统的基点和基面有哪些?其特性如何?答:理想光学系统的基点包括物方焦点、像方焦点;物方主点、像方主点;物方节点、像方节点。
基面包括:物方焦平面、像方焦平面;物方主平面、像方主平面;物方节平面、像方节平面。
入射光线(或其延长线)过焦点时,其共轭光线平行与光轴;入射光线过节点时,其共轭光线与之平行;焦平面上任一点发出的同心光束的共轭光束为平行光束;物方主平面与像方主平面共轭,且垂轴放大率为1。
7、对目视光学仪器的共同要求是什么?答:视放大率||Γ应大于1。
第一章几何光学基本定律与成像概念1、波面:某一时刻其振动位相相同的点所构成的等相位面成为波阵面,简称波面。
光的传播即为光波波阵面的传播。
2、光束:与波面对应的所有光线的集合。
3、波面分类:a)平面波:对应相互平行的光线束(平行光束)b)球面波:对应相较于球面波球心的光束(同心光束)c)非球面波4、全反射发生条件:a)光线从光密介质向光疏介质入射b)入射角大于临界角5、光程:光在介质中传播的几何路程l与所在介质的折射率n的乘积s。
光程等于同一时间内光在真空中所走的几何路程。
6、费马原理:光从一点传播到另一点,期间无论经过多少次折射和反射,其光程为极值。
7、马吕斯定律:光线束在各向同性的均匀介质中传播时,始终保持着与波面的正交性,并且入射波面与出射波面对应点之间的光程均为定值。
8、完善像:a)一个被照明物体每个物点发出一个球面波,如果该球面波经过光学系统后仍为一球面波,那么对应光束仍为同心光束,则称该同心光束的中心为物点经过光学系统后的完善像点。
b)每个物点的完善像点的集合就是完善像。
c)物体所在空间称为物空间,像所在空间称为像空间。
10、完善成像条件:a)入射波面为球面波时,出射波面也为球面波。
b)或入射光为同心光束时,出射光也为同心光束。
c)或物点A1及其像点之间任意两条光路的光程相等。
11、物像虚实:几个光学系统组合在一起时,前一系统形成的虚像应看成当前系统的实物。
12、子午面:物点和光轴的截面。
13、决定光线位置的两个参量:a)物方截距:曲面顶点到光线与光轴交点A的距离,用L表示。
b)物方孔径角:入射光线与光轴的夹角,用U表示。
14、符号规则a)沿轴线段:以折射面顶点为原点,由顶点到光线与光轴交点或球心的方向于光线传播方向相同时取证,相反取负b)垂轴线段:以光轴为基准,在光轴上方为正,下方为负。
c)夹角:i.优先级:光轴》光线》法线。
ii.由优先级高的以锐角方向转向优先级低的。
iii.顺时针为正,逆时针为负。
15、球差:单个折射球面对轴上物点成像是不完善的。
球差是固有缺陷。
16、高斯像:轴上物点在近轴区以细光束成像是完善的,这个像称为高斯像。
a)通过高斯像点且垂直于光轴的平面称为高斯像面。
b) 这样一对构成物象关系的点称为共轭点。
17、阿贝不变量Q :物空间与像空间的阿贝不变量相等,仅随共轭点的位置而变。
Q lr n l r n =-=-)11()'11(' 18、垂轴放大率β:β为像的大小与物体大小之比a) ln nl ''y y'==β 由此可知,垂轴放大率仅取决于共轭面位置,在一堆共轭面上,β为常数,故像与物相似。
b) 成像特性:i. β>0,成正像,虚实相反;β<0,成倒像,虚实相同。
ii. |β|>1,成放大的像,反之成缩小的像。
19、轴向放大率α:物点沿光轴做微笑移动dl 时,引起的像点移动量dl'与物点移动量之比。
a) 222''''βαnn l n nl dl dl === b) 折射球面的轴向放大率恒为正20、角放大率:在近轴区内,一对共轭光线与光轴的夹角u'与u 的比值,用γ表示。
a) βγ1'''n n l l u u === b) 角放大率表示折射球面将光束变宽或变细的能力c) 角放大率只与共轭点的位置有关,与孔径角无关21、三个放大率的关系:βββαγ==''2n n n n 22、由'''''u n nu l n nl y y ===β得J y u n nuy =='''。
该式表明实际光学系统在近轴区成像时,在物象共轭面内,物体大小y 、成像光束的孔径角u 和物体所在材质折射率n 的乘积为一常数。
该常数J 称为拉格朗日-赫姆霍兹不变量,简称拉赫不变量。
23、球面反射镜的情况:a) 物像位置关系:rl l 21'1=+ b) 成像放大率: βγβαβ1'''''222-==-=-==-==u u ll dl dl ll y y c) 球面镜的拉兹不变量:''y u uy J -==24、共轴球面系统过渡公式a) i i i d l l -=+'1 '1i i i i u d h h -=+第二章 理想光学系统1、理想光学系统:将一般仅在光学系统近轴区存在的完善成像,拓展成在任意大的空间中以任意宽的光束都成完善像的理想模型。
性质:a) 位于光轴上的物点对应的共轭像点也必然位于光轴上;位于过光轴的某一个截面内的物点对应的共轭像点必位于该平面的共轭像面内;过光轴的任意截面成像性质都是相同的。
b) 垂直于光轴的平面物所称的共轭平面像的几何形状完全与物相似。
c) 如果已知两对共轭面的位置和放大率,或者一对共轭面的位置和放大率以及轴上两对共轭点的位置,则其他一切物点的像点都可以根据这些已知的共轭面和共轭点来表示。
这些已知的共轭面和共轭点分别称为共轴系统的“基面”和“基点”。
19、无限远轴上物点和它对应的像点F'a) 无限远轴上物点发出的光线都与光轴平行b) 无限远轴上物点的像点F'称为像方焦点。
过F'作垂直于光轴的平面,称为像方焦平面。
c) 将入射光线(平行于光轴的)与出射光线反向延长,则两光线必交于一点,设此点为Q',过Q'作垂直于光轴的平面交光轴于H',则H'称为像方主点,Q'H'平面称为像方主平面,从主点H'到焦点F'的距离称为像方焦距,用'f 表示。
'tan 'U h f = d) 将入射光线与出射光线(平行于光轴的)反向延长,则两光线必交于一点,设此点为Q ,过Q 作垂直于光轴的平面交光轴于H ,则H'称为物方主点,QH 平面称为物方主平面,从主点H 到焦点F 的距离称为物方焦距,用'f 表示。
Uh f tan = 20、图解法求像a) 已知一个理想光学系统的主点(主面)和焦点的位置,利用光线通过他们之后的性质,对物空间给定的点、线、面,通过画图追踪典型光线求出像的方法。
b) 平行于光轴入射的光线,经过系统后过像方焦点。
c) 过物方焦点的光线,经过系统后平行于光轴。
d) 倾斜于光轴入射的平行光束经过系统后交于像方焦平面上一点。
e) 自物方焦平面上发出的光束经系统后成倾斜于光轴的平行光束。
f) 共轭光线在主面上的投射高度相等。
21、解析法求像a) 牛顿公式:物和像的位置相对于光学系统的焦点来确定,以物点到物方焦点距离为物距,用x 表示;以像点到像方焦点距离为像距,用x'表示。
正负号以响应焦点为原点确定i. 公式:''ff xx =; 垂轴放大率:'''f x x f y y -=-==β b) 高斯公式:以l 表示物点到物方主点的距离,以'l 表示像点到像方主点的距离;正负以相应主点为原点确定i. 公式:1''=+l f l f 垂轴放大率:ll f f y y '''-==β22、多光组组成的理想光学系统的成像a) 光组:一个光学系统可由一个或几个部件组成,每个部件可以由一个或几个透镜组成,这些部件被称为光组。
b) 过渡公式:前一光组的像即为后一光组的物,两光组的相互位置以距离121'd H H =(前一光组的像方主点到后一光组的物方主点)表示。
c) 过渡关系:112112''∆-=-=x x d l l 其中1∆表示第一光组像方焦点到第二光组物方焦点的距离,称为焦点间隔或光学间隔。
正负以前一光组像方焦点为原点确定。
d) 过渡公式一般形式:11111'''+----+-=∆∆-=-=i i i i i i i i i i f f d x x d l l23、理想光学系统两焦距之间的关系a) 由'tan 'tan U l h U l ==或'tan )''(tan )(U f x U f x +=+代入)'/(y y f x -=和)/'(''y y f x -=得 'tan ''tan U y f U fy -=(近轴区中:'''u y f fyu -=)b) 用'''u y f fyu -=和拉兹公式'''u y n nyu =比较得nn f f ''-=。
c) 若光学系统中包括反射面,两焦距间的关系由反射面个数决定:n n f f k ')1('1+-= d) 理想光学系统的拉兹公式:'tan ''tan U y n U ny =24、理想光学系统的放大率a) 轴向放大率i. dldl dx dx ''==α,微分牛顿公式得:0''=+dx x xdx 即x x '-=α ii. 代入牛顿公式的垂轴放大率公式l l f f y y '''-==β得22''ββαn n f f =-= b) 角放大率:代入拉兹公式得:βγ1'tan 'tan n n U U == c) 理想光学系统的三种放大率之间关系式:βαγ=d) 光学系统的节点i. 光学系统中角放大率等于⨯+1的一堆共轭点称为节点。
若物像空间戒指相同则βγ1=,进一步当1=β时,即考虑共轭面为主平面时,1=γ,此时主点即为节点。
物理意义:过节点(此处为主点)的入射光线经过系统后出射方向不变。
ii. 物像方空间折射率不等时,角放大率1=γ的物像共轭点不再与主点重合,而是'f x J =和f x J ='。
e) 一对节点、一对主点、一对焦点,统称光学系统的基点。
25、用平行光管测定焦距a) 一束与光轴成ω角入射的平行光束经系统以后会聚于焦平面上的一点,即无限远轴外物点的像,像高y'是由这束平行光束中过节点的光线决定的,如果被测系统放在空气中,则主点与节点重合,得:ωtan ''f y -=。
b) 只要给被测系统提供一与光轴倾斜成已知角度ω的平行光束,测出其在焦平面上的像高,就可算出焦距。
公式:''12y yf f = 26、光焦度:通常用φ表示像方焦距的倒数,'1f =Φ。