下载文档原格式
电气学科大类级《信号与控制综合实验》课程实验报告(基本实验一:信号与系统基本实验)姓名学号专业班号同组者1 学号专业班号同组者2 学号专业班号指导教师日期实验成绩评阅人综合实验和实验报告要求信号与控制综合实验，是集多门技术基础课程以及其它延伸课程理论于一体的综合性实验课程，需要综合多门学科理论知识和实验方法来体现，因此，实验目的不是简单的课程理论验证和练习，而是综合应用、研究开发、设计创新。
应采用尽可能好的设计，使所设计的电路和系统达到要实现的功能，步骤和方案自行拟定，实现对设计思路的实验验证。
完成多个实验项目的，应将实验内容整理综合后写成一份总报告，以利于锻炼整理归纳和总结能力，在总报告中以第二级标题形式依次写下所完成的实验项目、内容及实验设计过程。
实验报告按“题目、目录、正文（分所完成的各实验项目）、结论、心得与自我评价、参考文献”6个部分撰写；正文主要包括以下几个内容：任务和目标、总体方案设计（原理分析与方案设计特点，选择依据和确定）、方案实现和具体设计（过程）、实验设计与实验结果、结果分析与讨论。
（格式方面请注意：每个图应该有图号和图名，位于图的下方，同一图号的分图应在同一页，不要跨页；每个表应该有表号和表名，位于表的上方，表号表名与表（数据）也应在同一页，不要跨页；建议各部分题目采用四号黑体、设计报告内容文字采用小四号宋体）注：报告中涉及实验指导书或教材内容，只需注明引用位置，不必在报告中再加以阐述。
不得不加引用标记地抄袭任何资料。
每一基本实验部分按计划学时100分成绩计算（100％），需要完成60分的实验项目；实验报告、设计部分和创新研究内容另外计分（分别为10％、20％和10％）。
再按照学时比例与本课程其它部分实验综合成为总实验成绩。
每一部分实验均为：基本实验：0～60分，考核基本理论的掌握和基本操作技能、实验室道德规范；实验报告：0～10分，考核思考和总结表述能力；完成设计性实验：0～20分，评价设计能力；完成创新性实验：0～10分，鼓励创新。
《信号与系统》课程实验报告《信号与系统》课程实验报告一图1-1 向量表示法仿真图形2．符号运算表示法若一个连续时间信号可用一个符号表达式来表示，则可用ezplot命令来画出该信号的时域波形。
上例可用下面的命令来实现（在命令窗口中输入，每行结束按回车键）。
t=-10:0.5:10;f=sym('sin((pi/4)*t)');ezplot(f,[-16,16]);仿真图形如下：图1-2 符号运算表示法仿真图形三、实验内容利用MATLAB实现信号的时域表示。
三、实验步骤该仿真提供了7种典型连续时间信号。
用鼠标点击图0-3目录界面中的“仿真一”按钮，进入图1-3。
图1-3 “信号的时域表示”仿真界面图1-3所示的是“信号的时域表示”仿真界面。
界面的主体分为两部分：1) 两个轴组成的坐标平面（横轴是时间，纵轴是信号值）；2) 界面右侧的控制框。
控制框里主要有波形选择按钮和“返回目录”按钮，点击各波形选择按钮可选择波形，点击“返回目录”按钮可直接回到目录界面。
图1-4 峰值为8V，频率为0.5Hz，相位为180°的正弦信号图1-4所示的是正弦波的参数设置及显示界面。
在这个界面内提供了三个滑动条，改变滑块的位置，滑块上方实时显示滑块位置代表的数值，对应正弦波的三个参数：幅度、频率、相位；坐标平面内实时地显示随参数变化后的波形。
在七种信号中，除抽样函数信号外，对其它六种波形均提供了参数设置。
矩形波信号、指数函数信号、斜坡信号、阶跃信号、锯齿波信号和抽样函数信号的波形分别如图1-5～图1-10所示。
图1-5 峰值为8V，频率为1Hz，占空比为50%的矩形波信号图1-6 衰减指数为2的指数函数信号图1-7 斜率=1的斜坡信号图1-8 幅度为5V，滞后时间为5秒的阶跃信号图1-9 峰值为8V，频率为0.5Hz的锯齿波信号图1-10 抽样函数信号仿真途中，通过对滑动块的控制修改信号的幅度、频率、相位，观察波形的变化。
电气学科大类2012 级《信号与控制综合实验》课程实验报告(基本实验一:信号与系统基本实验)姓名丁玮学号U201216149 专业班号水电1204 同组者1 余冬晴学号U201216150 专业班号水电1204 同组者2 学号专业班号指导教师日期实验成绩评阅人实验评分表基本实验实验编号名称/内容实验分值评分实验一常用信号的观察实验二零输入响应、零状态相应及完全响应实验五无源滤波器与有源滤波器实验六LPF、HPF、BPF、BEF间的变换实验七信号的采样与恢复实验八调制与解调设计性实验实验名称/内容实验分值评分创新性实验实验名称/内容实验分值评分教师评价意见总分目录1.实验一常用信号的观察 (1)2.实验二零输入响应、零状态响应及完全响应 (4)3.实验五无源滤波器与有源滤波器 (7)4.实验六 LPF、HPF、BPF、BEF间的转换 (14)5.实验七信号的采样与恢复 (19)6.实验八调制与解调 (29)7.实验心得与自我评价 (33)8.参考文献 (34)实验一常用信号的观察一．任务与目标1.了解常见信号的波形和特点；2.了解常见信号有关参数的测量，学会观察常见信号组合函数的波形；3.学会使用函数发生器和示波器，了解所用仪器原理与所观察信号的关系；4.掌握基本的误差观察与分析方法。
二．总体方案设计1.实验原理描述信号的方法有许多种，可以用数学表达式（时间的函数），也可以使用函数图形（信号的波形）。
信号可以分为周期信号和非周期信号两种。
普通示波器可以观察周期信号，具有暂态拍摄功能的示波器可以观察到非周期信号的波形。
目前，常用的数字示波器可以方便地观察周期信号及非周期信号的波形。
2.总体设计⑴观察常用的正弦波、方波、三角波、锯齿波等信号及一些组合函数的波形，如y=sin(nx)+cos(mx)。
⑵用示波器测量信号，读取信号的幅值与频率。
三．方案实现与具体设计1.用函数发生器产生正弦波，并且设定波形的峰值及频率，用示波器观察并记录波形，测量和读取信号的幅值与频率；2.用函数发生器产生方波，并且设定波形的峰值及频率，用示波器观察并记录波形，测量和读取信号的幅值与频率；3.用函数发生器产生三角波，并且设定波形的峰值及频率，用示波器观察并记录波形，测量和读取信号的幅值与频率；4.用函数发生器产生锯齿波，并且设定波形的峰值及频率，用示波器观察并记录波形，测量和读取信号的幅值与频率；5.用函数发生器产生两个不同频率的正弦波，分别设定波形的峰值及频率，用示波器叠加波形，并观察组合函数的波形。
信号与系统实验报告一、实验目的(1) 理解周期信号的傅里叶分解，掌握傅里叶系数的计算方法；(2)深刻理解和掌握非周期信号的傅里叶变换及其计算方法；(3) 熟悉傅里叶变换的性质，并能应用其性质实现信号的幅度调制；(4) 理解连续时间系统的频域分析原理和方法，掌握连续系统的频率响应求解方法，并画出相应的幅频、相频响应曲线。
二、实验原理、原理图及电路图(1) 周期信号的傅里叶分解设有连续时间周期信号()f t ，它的周期为T ，角频率22fT，且满足狄里赫利条件，则该周期信号可以展开成傅里叶级数，即可表示为一系列不同频率的正弦或复指数信号之和。
傅里叶级数有三角形式和指数形式两种。
1）三角形式的傅里叶级数：01212011()cos()cos(2)sin()sin(2)2cos()sin()2n n n n a f t a t a t b t b t a a n t b n t 式中系数n a ，n b 称为傅里叶系数，可由下式求得：222222()cos(),()sin()T T T T nna f t n t dtb f t n t dtTT2）指数形式的傅里叶级数：()jn tn nf t F e式中系数n F 称为傅里叶复系数，可由下式求得：221()T jn tT nF f t edtT周期信号的傅里叶分解用Matlab进行计算时，本质上是对信号进行数值积分运算。
Matlab中进行数值积分运算的函数有quad函数和int函数。
其中int函数主要用于符号运算，而quad函数（包括quad8，quadl）可以直接对信号进行积分运算。
因此利用Matlab进行周期信号的傅里叶分解可以直接对信号进行运算，也可以采用符号运算方法。
quadl函数(quad系)的调用形式为：y＝quadl(‘func’,a,b)或y＝quadl(@myfun,a,b)。
其中func是一个字符串，表示被积函数的.m文件名（函数名）；a、b分别表示定积分的下限和上限。
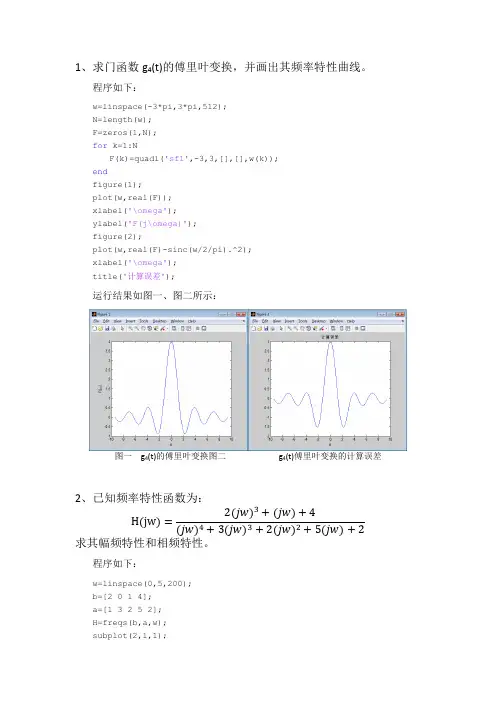
1、求门函数g4(t)的傅里叶变换，并画出其频率特性曲线。
程序如下：w=linspace(-3*pi,3*pi,512);N=length(w);F=zeros(1,N);for k=1:NF(k)=quadl('sf1',-3,3,[],[],w(k));endfigure(1);plot(w,real(F));xlabel('\omega');ylabel('F(j\omega)');figure(2);plot(w,real(F)-sinc(w/2/pi).^2);xlabel('\omega');title('计算误差');运行结果如图一、图二所示：图一g4(t)的傅里叶变换图二g4(t)傅里叶变换的计算误差2、已知频率特性函数为：H(jw)=2(jw)3+jw+4(jw)4+3(jw)3+2(jw)2+5jw+2求其幅频特性和相频特性。
程序如下：w=linspace(0,5,200);b=[2 0 1 4];a=[1 3 2 5 2];H=freqs(b,a,w);subplot(2,1,1);plot(w,abs(H));set(gca,'xtick',[0 1 2 3 4 5]);set(gca,'ytick',[0 0.4 0.707 1]);xlabel('\omega');ylabel('|H(j\omega)|');subplot(2,1,2);plot(w,angle(H));set(gca,'xtick',[0 1 2 3 4 5]);xlabel('\omega');ylabel('\phi(\omega)');运行结果如图三所示：图三幅频特性和相频特性3、设H s=s(s−p1)(s−p2)设①p1=-2，p2=-30；②p1=-2，p2=3（1）针对极点参数①②，画出系统零、极点分布图，判断该系统稳定性。
数字信号处理课程实验报告实验一 离散时间信号和系统响应一. 实验目的1. 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解2. 掌握时域离散系统的时域特性3. 利用卷积方法观察分析系统的时域特性4. 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号及系统响应进行频域分析二、实验原理1. 采样是连续信号数字化处理的第一个关键环节。
对采样过程的研究不仅可以了解采样前后信号时域和频域特性的变化以及信号信息不丢失的条件，而且可以加深对离散傅里叶变换、Z 变换和序列傅里叶变换之间关系式的理解。
对连续信号()a x t 以T 为采样间隔进行时域等间隔理想采样，形成采样信号： 式中()p t 为周期冲激脉冲，()a x t 为()a x t 的理想采样。
()a x t 的傅里叶变换为()a X j Ω：上式表明将连续信号()a x t 采样后其频谱将变为周期的，周期为Ωs=2π/T 。
也即采样信号的频谱()a X j Ω是原连续信号xa(t)的频谱Xa(jΩ)在频率轴上以Ωs 为周期，周期延拓而成的。
因此，若对连续信号()a x t 进行采样，要保证采样频率fs ≥2fm ，fm 为信号的最高频率，才可能由采样信号无失真地恢复出原模拟信号ˆ()()()a a xt x t p t =1()()*()21()n a a a s X j X j P j X j jn T π∞=-∞Ω=ΩΩ=Ω-Ω∑()()n P t t nT δ∞=-∞=-∑计算机实现时，利用计算机计算上式并不方便，因此我们利用采样序列的傅里叶变换来实现，即而()()j j n n X e x n e ωω∞-=-∞=∑为采样序列的傅里叶变换2. 时域中，描述系统特性的方法是差分方程和单位脉冲响应，频域中可用系统函数描述系统特性。
已知输入信号，可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应。
福建xx大学xx学院信息工程类实验报告课程名称：信号与系统姓名：XXX系：电子信息工程专业：电子信息工程年级：XXX级学号：XXX指导教师：XXX职称：讲师XXX年12 月17日实验项目列表XXX 信息工程类实验报告系： 电子信息工程 专业： 电子信息工程 年级： 07级 姓名： XXX 学号： XXX 实验课程： 信号与系统实验室号：_信号与系统实验室 实验设备号： 01 实验时间： 11.19 指导教师签字： 成绩：实验一 函数信号发生器1、 实验目的1）了解单片多功能集成电路函数信号发生器的功能及特点。
2）熟悉信号与系统实验箱信号产生和测试的方法。
2、 实验仪器1）信号与系统实验箱一台。
2）20MHz 双踪示波器一台。
3、 实验原理ICL8038是单片机集成函数信号发生器，其内部框图如图1.1所示。
它由恒流源1I 和2I 、电压比较器A 和B 、触发器、缓冲器和三角波变正弦波电路等组-V EE图1.1 ICL8038原理方框图外接电容C 由两个恒流源充电和放电，电压比较器A 、B 的阀值分别为电源电压(指EE cc U U +)的2/3和1/3。
恒流源1I 和2I 的大小可通过外接电阻调节，但必须12I I >。
当触发器的输出为低电平时，恒流源2I 断开，恒流源1I 给C 充电，它的两端电压UC 随时间线性上升，当UC 达到电源电压的2/3时，电压比较器A 的输出电压发生跳变，使触发器输出由低电平变为高电平，恒流源C 接通，由于12I I >(设122I I =)，恒流源2I 将电流21I 加到C 上反充电，相当于C 由一个净电流I 放电，C 两端的电压UC 又转为直线下降。
当它下降到电源电压的1/3时，电压比较器B 的输出电压发生跳变，使触发器的输出由高电平跳变为原来的低电平，恒流源2I 断开，1I 再给C 充电，…如此周而复始，产生振荡。
若调整电路，使122I I =，则触发器输出为方波，经反相缓冲器由管脚⑨输出方波信号。
《信号与系统》上机实验实验一连续时间信号的表示及可视化一．实验目的熟练掌握连续时间信号的表示及可视化处理。
二．实验源程序δf(t))=)(tf=@(t)dirac(t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)= ε(t)（f=Heaviside(n)）f=@(t)heaviside(t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)=at e(分别取a>0及a<0)a=1时f=@(t)exp(t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标a=-1时f=@(t)exp(-t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)=R(t)t=-5:0.01:5; %设定时间变量t的范围及步长y=rectpuls(t,2); %用rectpuls（t a)命令表示门函数，默认以零点为中心，宽度为aplot(t,y); %用plot函数绘制连续函数grid on; %显示网格命令title('门函数'); %用title函数设置图形的名称axis([-5 5 -0.5 1.5]);f(t)=Sa(wt)w=5时，f=Sa(5*t)f=@(t)Sinc(5*t) %定义函数ezplot(f,[-5:5]); %利用ezplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标axis([-5 5 -1.2 1.2])w=8时，f=Sa(8*t)f=@(t)sinc(8*t) %定义函数ezplot(f,[-4:4]); %利用eaplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标f(t)=Sin(2πft)(分别画出不同周期个数的波形)f(t)=Sin(t)f=@(t)sin(t) %定义函数ezplot(f,[-15:15]); %利用eaplot( )命令绘制连续图形xlabel('(t)'); %横坐标ylabel('(f)'); %纵坐标axis([-15 15 -1.2 1.2])三．程序运行结果(1)(2)（3）-5-4-3-2-1012345-1-0.8-0.6-0.4-0.200.20.40.60.81(t)dirac(t)(f )-5-4-3-2-101234500.20.40.60.81(t)heav iside(t)(f )（4）-5-4-3-2-1012345010********607080(t)exp(t)(f )-5-4-3-2-1012345010********607080(t)exp(-t)(f )（5）-5-4-3-2-1012345-1-0.8-0.6-0.4-0.200.20.40.60.81(t)Sinc(5 t)(f )(6)-4-3-2-101234 -1-0.8-0.6-0.4-0.20.20.40.60.81(t)sinc(8 t)(f)-15-10-5051015 -1-0.8-0.6-0.4-0.20.20.40.60.81(t)sin(t)(f)实验二离散时间信号的表示及可视化一．实验目的学会对离散时间信号进行标识和可视化处理。
信号与系统实验报告目录1. 内容概要 (2)1.1 研究背景 (3)1.2 研究目的 (4)1.3 研究意义 (4)2. 实验原理 (5)2.1 信号与系统基本概念 (7)2.2 信号的分类与表示 (8)2.3 系统的分类与表示 (9)2.4 信号与系统的运算法则 (11)3. 实验内容及步骤 (12)3.1 实验一 (13)3.1.1 实验目的 (14)3.1.2 实验仪器和设备 (15)3.1.4 实验数据记录与分析 (16)3.2 实验二 (16)3.2.1 实验目的 (17)3.2.2 实验仪器和设备 (18)3.2.3 实验步骤 (19)3.2.4 实验数据记录与分析 (19)3.3 实验三 (20)3.3.1 实验目的 (21)3.3.2 实验仪器和设备 (22)3.3.3 实验步骤 (23)3.3.4 实验数据记录与分析 (24)3.4 实验四 (26)3.4.1 实验目的 (27)3.4.2 实验仪器和设备 (27)3.4.4 实验数据记录与分析 (29)4. 结果与讨论 (29)4.1 实验结果汇总 (31)4.2 结果分析与讨论 (32)4.3 结果与理论知识的对比与验证 (33)1. 内容概要本实验报告旨在总结和回顾在信号与系统课程中所进行的实验内容，通过实践操作加深对理论知识的理解和应用能力。
实验涵盖了信号分析、信号处理方法以及系统响应等多个方面。
实验一：信号的基本特性与运算。
学生掌握了信号的表示方法，包括连续时间信号和离散时间信号，以及信号的基本运算规则，如加法、减法、乘法和除法。
实验二：信号的时间域分析。
在本实验中，学生学习了信号的波形变换、信号的卷积以及信号的频谱分析等基本概念和方法，利用MATLAB工具进行了实际的信号处理。
实验三：系统的时域分析。
学生了解了线性时不变系统的动态响应特性，包括零状态响应、阶跃响应以及脉冲响应，并学会了利用MATLAB进行系统响应的计算和分析。
信号与系统实验报告一、信号的时域基本运算1．连续时间信号的时域基本运算两实验之一实验分析：输出信号值就等于两输入信号相加（乘）。
由于b=2，故平移量为2时，实际是右移1，符合平移性质。
两实验之二心得体会：时域中的基本运算具有连续性，当输入信号为连续时，输出信号也为连续。
平移，伸缩变化都会导致输出结果相对应的平移伸缩。
2.离散时间信号的时域基本运算两实验之一实验分析：输出信号的值是对应输入信号在每个n值所对应的运算值，当进行拉伸变化后，n值数量不会变，但范围会拉伸所输入的拉伸系数。
两实验之二心得体会：离散时间信号可以看做对连续时间信号的采样，而得到的输出信号值，也可以看成是连续信号所得之后的采样值。
二、连续信号卷积与系统的时域分析1.连续信号卷积积分两实验之一实验分析：当两相互卷积函数为冲激函数时，所卷积得到的也是一个冲激函数，且该函数的冲激t值为函数x，函数y冲激t值之和。
两实验之二心得体会：连续卷积函数每个t值所对应的卷积和可以看成其中一个在k值取得的函数与另外一个函数相乘得到的一个分量函数，并一直移动k值直至最后，最后累和出来的最终函数便是所得到的卷积函数。
3.RC电路时域积分两实验之一实验分析：全响应结果正好等于零状态响应与零输入响应之和。
两实验之二心得体会：具体学习了零状态，零输入，全响应过程的状态及变化，与之前所学的电路知识联系在一起了。
三、离散信号卷积与系统的时域分析1.离散信号卷积求和两实验之一实验分析：输出结果的n值是输入结果的k号与另一个n-k的累和两实验之二心得体会：直观地观察到卷积和的产生，可以看成连续卷积的采样形式，从这个方面去想，更能深入地理解卷积以及采样的知识。
2.离散差分方程求解两实验之一实验分析：其零状态响应序列为0 0 4 5 7.5，零输入响应序列为2 4 5 5.5 5.75，全状态响应序列为2 4 9 10.5 13.25，即全状态=零输入+零状态。
两实验之二心得体会：求差分方程时，可以根据全状态响应是由零输入输入以及零状态相加所得，分开来求，同时也加深了自己对差分方程的求解问题的理解。
实验一连续时间信号的时域基本运算一、实验目的（1）掌握连续时间信号时域运算的基本方法；（2）掌握相关函数的调用格式及作用；（3）掌握连续信号的基本运算。
二、实验原理信号的基本运算包括信号的相加（减）和相乘(除).信号的时域变换包括信号的平移、翻转、倒相以及尺度变换。
（1）加减： f(t)=f1(t)±f2(t)（2）乘: f(t)=f1(t)×f2(t)（3）延时或平移：f(t)→(t-t0) t0>0时右移；t0<0时左移（4）翻转： f(t)→f(-t)（5）尺度变换：f(t)→ f(at) |a|>1时尺度缩小；|a|<1时尺度放大；a<0时，尺度翻转。
（6）标量乘法：f(t)→af(t)（7）倒相： f(t)→-f(t)（8）微分： f(t)→df(t)/dt（9）积分： f(t)→∫t -∞f(t)d(t)三、涉及的MATLAB函数及其运算1、stepfun函数功能：产生一个阶跃信号。
调用格式：Stepfun(t,t0)其中，t是时间区间，在该区间内阶跃信号一定会产生；t是信号发生从0到1跳跃的时刻。
2、diff函数调用格式：diff (f) : 求函数f对预设独立变数的一次微分值。
diff (f, ’t’) : 求函数f对独立变数t的一次微分值。
3、int函数调用格式:Int（f）: 函数f对预设独立变数的积分值。
Int(f,’t’): 函数f对独立变数t的积分值。
4、heaviside函数Heaviside（t）:产生没有移位的阶跃信号。
Heaviside（t-k）:产生向右平移K单位的阶跃信号。
四、实验内容与方法1、验证性实验（1）移位实现连续信号的移位，即f(t-t0),或者f(t+t0);常数t0>0。
MATLAB程序clear allt=0:0.0001:2y=sin(2*pi*(t));y1=sin(2*pi*(t-0.2));plot(t,y,'-',t,y1,'--');ylabel('f(t)');xlabel('t');title('信号的移位')运行结果：（2）翻转（信号的翻转就是将信号的波形以纵轴为对称轴翻转180度，将信号f(t)的自变量t替换为-t即可得到其翻转信号。
）MATLAB程序：clear all;t=0:0.02:1;t1=-1:0.02:0;g1=3*t;g2=3*(-t1);plot(t,g1,'--',t1,g2);grid on;xlabel('t');ylabel('g(t)');title('信号的反折');运行结果;（3）尺度变换将信号f(t)中的自变量t替换为at。
MATLAB程序：clear all;t=0:0.001:1;a=2;y=sin(2*pi*t);y1=sin(2*a*pi);subplot(211)plot(t,y);ylabel('y(t)');xlabel('t');title('尺度变换');subplot(212)plot(t,y1);ylabel('y1(t)');xlabel('t');运行结果：（4）综合MATLAB程序syms tf=sym('(t/2+1)*(heaviside(t+2)-heaviside(t-2))')subplot(2,3,1);ezplot(f,[-3,3]);title('f');y1=subs(f,t,t+2);subplot(2,3,2);ezplot(y1,[-5,1]);title('y1');y2=subs(f,t,t-2);subplot(2,3,3);ezplot(y2,[-1,5]);title('y2');y3=subs(f,t,-t);subplot(2,3,4);ezplot(y1,[-3,3]);title('y3');y4=subs(f,t,2*t);subplot(2,3,5);ezplot(y1,[-2;2]);title('y4');y5=-f;subplot(2,3,6);ezplot(y1,[-3,3]);title('y5');表达式f =(t/2+1)*(heaviside(t+2)-heaviside(t-2))运行结果：2、程序设计实验syms tf=sym('(-2*t/3+2/3)*(heaviside(t+2)-heaviside(t-1))')subplot(2,4,1);ezplot(f,[-3,3]);title('f');y1=subs(f,t,-t);subplot(2,4,2);ezplot(y1,[-3,3]);title('y1');y2=subs(f,t,-t+2);subplot(2,4,3);ezplot(y2,[-1,5]);title('y2');y3=subs(f,t,-t-2);subplot(2,4,4);ezplot(y1,[-2,4]);title('y3');y4=subs(f,t,2*t);subplot(2,4,5);ezplot(y1,[-2,3]);title('y4');y5=subs(f,t,1/2*t);subplot(2,4,6);ezplot(y1,[-2,4]);title('y5');y6=subs(f,t,t-2);subplot(2,4,7);ezplot(y1,[-2,3]);title('y6');y7=subs(f,t,-1/2*t+1);subplot(2,4,8);ezplot(y1,[-4,8]);title('y7运行结果：五、实验总结-通过本次实验学会了连续时间信号时域运算的基本方法，掌握了stepfun函数，diff函数、int函数、heaviside函数调用格式以及作用，并且掌握了连续信号的基本运算。
实验二LTI系统的响应一、实验目的1. 熟悉连续时间系统的单位冲激响应、阶跃响应的意义及求解方法2. 熟悉连续（离散）时间系统在任意信号激励下响应的求解方法3. 熟悉应用MATLAB实现求解系统响应的方法二、实验原理1.连续时间系统对于连续的LTI系统，当系统输入为f(t)，输出为y(t)，则输入与输出之间满足如下的线性常系数微分方程：，当系统输入为单位冲激信号δ(t)时产生的零状态响应称为系统的单位冲激响应，用h(t)表示。
若输入为单位阶跃信号ε(t)时，系统产生的零状态响应则称为系统的单位阶跃响应，记为g(t)，如下图所示。
系统的单位冲激响应h(t)包含了系统的固有特性，它是由系统本身的结构及参数所决定的，与系统的输入无关。
我们只要知道了系统的冲激响应，即可求得系统在不同激励下产生的响应。
因此，求解系统的冲激响应h(t)对我们进行连续系统的分析具有非常重要的意义。
在MATLAB中有专门用于求解连续系统冲激响应和阶跃响应，并绘制其时域波形的函数impulse( ) 和step( )。
如果系统输入为f(t)，冲激响应为h(t)，系统的零状态响应为y(t)，则有：y(t)h(t)f(t)。
若已知系统的输入信号及初始状态，我们便可以用微分方程的经典时域求解方法，求出系统的响应。
但是对于高阶系统，手工计算这一问题的过程非常困难和繁琐。
在MATLAB中，应用lsim( )函数很容易就能对上述微分方程所描述的系统的响应进行仿真，求出系统在任意激励信号作用下的响应。
lsim( )函数不仅能够求出连续系统在指定的任意时间范围内系统响应的数值解，而且还能同时绘制出系统响应的时域波形图。
以上各函数的调用格式如下：⑴impulse( ) 函数函数impulse( )将绘制出由向量a和b所表示的连续系统在指定时间范围内的单位冲激响应h(t)的时域波形图，并能求出指定时间范围内冲激响应的数值解。
impulse(b,a) 以默认方式绘出由向量a和b所定义的连续系统的冲激响应的时域波形。
impulse(b,a ,t0) 绘出由向量a和b所定义的连续系统在0 ~ t0时间范围内冲激响应的时域波形。
impulse(b,a,t1:p:t2) 绘出由向量a和b所定义的连续系统在t1 ~ t2时间范围内，并且以时间间隔p均匀取样的冲激响应的时域波形。
y=impulse(b,a,t1:p:t2) 只求出由向量a和b所定义的连续系统在t1 ~ t2时间范围内，并且以时间间隔p均匀取样的冲激响应的数值解，但不绘出其相应波形。
⑵step( ) 函数函数step( )将绘制出由向量a和b所表示的连续系统的阶跃响应，在指定的时间范围内的波形图，并且求出数值解。
和impulse( )函数一样，step( )也有如下四种调用格式：step( b,a)step(b,a,t0)step(b,a,t1:p:t2)y=step(b,a,t1:p:t2)上述调用格式的功能和impulse( )函数完全相同，所不同只是所绘制（求解）的是系统的阶跃响应g(t)，而不是冲激响应h(t)。
⑶lsim( )函数根据系统有无初始状态，lsim( )函数有如下两种调用格式：①系统无初态时，调用lsim( )函数可求出系统的零状态响应，其格式如下：lsim(b,a,x,t)绘出由向量a和b所定义的连续系统在输入为x和t所定义的信号时，系统零状态响应的时域仿真波形，且时间范围与输入信号相同。
其中x和t是表示输入信号的行向量，t为表示输入信号时间范围的向量，x则是输入信号对应于向量t所定义的时间点上的取样值。
y=lsim(b,a,x,t) 与前面的impulse 和step函数类似，该调用格式并不绘制出系统的零状态响应曲线，而只是求出与向量t定义的时间范围相一致的系统零状态响应的数值解。
②系统有初始状态时，调用lsim( )函数可求出系统的全响应，格式如下：lsim(A,B,C,D,e,t,X0)绘出由系数矩阵A,B,C,D所定义的连续时间系统在输入为e和t所定义的信号时，系统输出函数的全响应的时域仿真波形。
t为表示输入信号时间范围的向量，e则是输入信号e(t)对应于向量t所定义的时间点上的取样值，X0表示系统状态变量X=[x1,x2,…..xn]'在t=0时刻的初值。
