线段的垂直平分线与角的平分线训练专题培优

线段的垂直平分线和角平分线专题训练及答案一、选择题（本大题共7小题，共21.0分）1.如图是一块三角形草坪，现要在草坪上建一个凉亭供大家休息．若要使凉亭到草坪三条边的距离都相等，则凉亭应建在三角形草坪()A. 三条角平分线的交点处B. 三条中线的交点处C. 三条高的交点处D. 三条边的垂直平分线的交点处2.下列说法错误的是()A. 等腰三角形底边上的高所在的直线是它的对称轴B. 等腰三角形底边上的中线所在的直线是它的对称轴C. 等腰三角形顶角的平分线所在的直线是它的对称轴D. 等腰三角形一个内角的平分线所在的直线是它的对称轴3.如图，在Rt△ABC中，∠A=90°，BD是角平分线，DE垂直平分BC，AD=3，则AC的长为()A. 9B. 5C. 4D. 3√34.如图，在△ABC中，AB的垂直平分线交BC于D，AC的垂直平分线交BC于E，∠BAC=124°，则∠DAE的度数为()A. 68°B. 62°C. 66°D. 56°5.如图，在△ABC中，CD平分∠ACB，交AB于点D，DE⊥AC于点E，若BC=2m+6，DE=m+3，则△BCD的面积为()A. 2m2−18B. 2m2+12m+18C. m2+9D. m2+6m+96.如图，P是∠BAC平分线上的点，PM⊥AB于M，PN⊥AC于N，则下列结论：①PM=PN；②AM=AN；③△APM≌△APN；④∠PAN+∠APM=90°．其中正确结论的个数是()A. 4个B. 3个C. 2个D. 1个7.如图所示，在△ABC中，AB=AC，AD是BC边上的高线，E，F是AD的三等分点，若△ABC的面积为12，则图中△BEF的面积为()A. 2B. 3C. 4D. 6二、解答题（本大题共10小题，共80.0分）8.直线OA，OB表示两条相互交叉的公路，点M，N表示两个蔬菜种植基地．现要建一个蔬菜批发市场P，要求它到两条公路的距离相等，且到两个蔬菜基地的距离也相等，请用尺规作图说明市场的位置．9.如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC，交BC于点D，DE⊥AB于点E.已知AB=10cm，求△DEB的周长．10.如图，已知AD是∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，且BE=CF，试判断BD和CD的数量关系，并说明理由．11.如图，要在街道旁修建一个奶站，向居民区A，B提供牛奶．奶站应建在什么地方才能使A，B到它的距离相等？12.A，B，C这3个村庄的位置如图所示，每两个村庄之间有公路相连，村民希望共同投资建一个货运中转站，使中转站的位置到3个村庄的距离相等．请你利用尺规作图确定中转站的位置．13.如图，四边形ABCD为矩形台球桌面，现有一白球M和黑球N，应怎样去打白球M，才能使白球M撞击桌边AB后反弹击中黑球N？请你画出白球M经过的路线．14.如图，在△ABC中，AB=AC，M是BC的中点，D，E分别是AB，AC边上的点，且BD=CE.试说明MD=ME．15.如图，在Rt△ABC中，∠C=90°，BC=3.∠CAB的平分线交BC于点D，DE是AB的垂直平分线，垂足为E．(1)求∠B度数．(2)求DE的长．16.如图，已知∠ABC，射线BC上一点D.求作：等腰三角形PBD，使线段BD为等腰三角形PBD的底边，点P在∠ABC内部，且点P到∠ABC两边的距离相等(保留作图痕迹，但不要求写作法)．17.如图，在Rt△ABC中，∠ACB=90°．(1)请用直尺和圆规按下列步骤作图，保留作图痕迹：①作∠ACB的平分线，交斜边AB于点D；②过点D作AC的垂线，垂足为点E．(2)在(1)作出的图形中，若CB=4，CA=6，则DE=______．答案和解析1.【答案】A【解析】[分析]本题主要考查的是角平分线的性质在实际生活中的应用．由于凉亭到草坪三条边的距离相等，所以根据角平分线上的点到角两边的距离相等，可知是三角形三条角平分线的交点．由此即可确定凉亭位置．[详解]解：∵凉亭到草坪三条边的距离相等，∴凉亭应建在三角形草坪的三条角平分线的交点处．故选A．2.【答案】D【解析】[分析]本题考查了等腰三角形的性质，属于基础题，解题的关键是了解对称轴是一条直线，难度不大．根据等腰三角形性质分别判断后即可确定正确的选项．[详解]解：A.等腰三角形底边上的高所在的直线是对称轴，正确；B.等腰三角形底边上的中线所在的直线是对称轴，正确；C.等腰三角形顶角的平分线所在的直线是对称轴，正确；D.等腰三角形顶角的平分线所在的直线是对称轴，如果这个内角是底角，不一定是它的对称轴，错误．故选D．3.【答案】A【解析】[分析]根据角平分线性质得出AD=DE，证明Rt△ADB≌Rt△EDB(HL)，得BE=AB，由DE 是BC的垂直平分线，得BC=2AB，所以∠C=30°，可得CD的长，从而得AC的长．本题考查了直角三角形的性质，线段垂直平分线的性质，角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．[详解]解：∵BD是角平分线，DE⊥BC，∠A=90°，∴DE=AD=3，在Rt△ADB和Rt△EDB中，∵{AD=DEBD=BD，∴Rt△ADB≌Rt△EDB(HL)，∴BE=AB，∵DE是BC的垂直平分线，∴CE=BE，∴BC=2AB，∴∠C=30°，∴CD=2DE=6，∴AC=CD+AD=6+3=9，故选：A．4.【答案】A【解析】[分析]根据三角形内角和定理求出∠B+∠C，根据线段垂直平分线的性质得到DA=DB，得到∠DAB=∠B，同理可得，∠EAC=∠C，结合图形计算，得到答案．本题考查的是线段的垂直平分线的性质、三角形内角和定理，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．[详解]解：∠B+∠C=180°−∠BAC=56°，∵AB的垂直平分线交BC于D，∴DA=DB，∴∠DAB=∠B，∵AC的垂直平分线交BC于E，∴EA=EC，∴∠EAC=∠C，∴∠DAE=∠BAC−(∠DAB+∠EAC)=124°−56°=68°．故选A．5.【答案】D【解析】[分析]过点D作DF⊥BC交CB的延长线于F，根据角平分线上的点到角的两边距离相等可得DE=DF，再根据三角形面积公式列式，然后根据多项式乘多项式法则进行计算即可得解．本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质并作辅助线构造出BC边上的高线是解题的关键．[详解]解：如图，过点D作DF⊥BC交CB的延长线于F，∵CD平分∠ACB，DE⊥AC，∴DE=DF，∴△BCD的面积=12·BC·DF=12(2m+6)(m+3)=m2+6m+9．故选D．6.【答案】A【解析】[分析]利用角平分线的性质结合全等三角形的判定与性质分析得出答案．此题主要考查了角平分线的性质，全等三角形的判定与性质，正确得出△APM≌△APN 是解题关键．[详解]解：∵P是∠BAC平分线上的点，PM⊥AB于M，PN⊥AC于N，∴∠MAP=∠NAP，∠AMP=∠ANP=90°，PM=PN，故①正确在△APM和△APN中{∠MAP=∠NAP ∠AMP=∠ANP AP=AP,∴△APM≌△APN(AAS)，故③正确，∴AM=AN，故②正确，∠APM=∠APN，∵∠PAN+∠APN=90°，∴∠PAN+∠APM=90°，故④正确，综上所述：正确的有4个．故选A．7.【答案】A【解析】[分析]本题考查了等腰三角形的性质及轴对称性质；利用对称发现并利用△ABD和△ACD的面积相等是正确解答本题的关键．由图，根据等腰三角形是轴对称图形知，△ABD和△ACD的面积相等，再根据点E、F，依此即可求解．是AD的三等分点，可得△BEF的面积为△ACD的面积的13[详解]解：∵在△ABC中，AB=AC，AD是BC边上的高，S△ABC=12，BC，S△ABD=6，∴BD=CD=12∵点E、F是AD的三等分点，AD，∴EF=13S△BEF=1S△ABD=2．2故选A．8.【答案】解：如图：P为所求做的点．【解析】本题考查了基本作图，理解角的平分线以及线段的垂直平分线的作图是关键．连接MN，先画出∠AOB的角平分线，然后再画出线段MN的中垂线．这两条直线的交点即为所求．9.【答案】解：∵AD平分∠BAC交BC于D，DE⊥AB，∠C=90°，∴CD=DE．又∵AD=AD，∴Rt△ACD≌△RtAED．∴AE=AC，∴△DEB的周长=DE+DB+EB=CD+DB+BE=BC+BE=AC+BE=AE+BE=AB=10cm．【解析】本题主要考查的是全等三角形的判定及性质，角平分线的性质等有关知识，由题意根据AD平分∠BAC交BC于D，DE⊥AB，∠C=90°，得到CD=DE，然后利用全等三角形的判定及性质得到AE=AC，最后利用三角形的周长公式进行求解即可．10.【答案】解：∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE=DF，∠E=∠DFC=90°．在△BED和△DFC中，DE=DF，∠E=∠DFC，BE=CF，∴△BED≌△DFC(SAS)，∴BD=CD．【解析】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即对应边、对应角相等)是解题的关键．由角平分线的性质可得DE=DF，再结合条件可证明Rt△BED≌Rt△CFD，即可求得BE=CF.11.【答案】解：连接AB，作AB的垂直平分线，与街道的交点为P，点P即为所求作的点．【解析】本题考查线段垂直平分线的性质，根据线段垂直平分线上的点到线段两端点的距离相等，可知此点P在AB的垂直平分线上即可解答，12.【答案】解：如图，【解析】此题主要考查了应用设计与作图，正确掌握线段垂直平分线的性质是解题关键．利用线段垂直平分线的性质进而得出AB，AC的垂直平分线进而得出交点，得出M即可．13.【答案】解：如图所示，作点N于AB的对称点N′，连接N′M，与AB相交于点O，连接MO，NO，就是白球路线．【解析】此题考查了轴对称作图，作点N于AB的对称点N′，连接N′M，与AB相交于点O，连接MO，NO，就是白球路线．14.【答案】证明：△ABC中，∵AB=AC，∴∠DBM=∠ECM．∵M是BC的中点，∴BM=CM．在△BDM和△CEM中，，∴△BDM≌△CEM(SAS)，∴MD=ME．【解析】本题主要考察等腰三角形的性质和全等三角形的判定与性质.根据等腰三角形的性质可证∠DBM=∠ECM，可证△BDM≌△CEM，可得MD=ME，即可解题．15.【答案】解：(1)∵DE是AB的垂直平分线，∴DA=DB，∴∠B=∠DAB．∵AD平分∠CAB，∴∠CAD=∠DAB．∵∠C=90°，∴3∠CAD=90°，∴∠CAD=30°，∴∠B=30°；(2)∵AD平分∠CAB，DE⊥AB，CD⊥AC，BD，∴CD=DE=12∵BC=3，∴CD=DE=1．【解析】本题主要考查线段垂直平分线的性质，熟悉掌握是关键．(1)由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°；(2)根据角平分线的性质即可得到结论．16.【答案】解：如图，△PBD即为所求作的三角形【解析】【分析】本题考查尺规作图.根据角平分线的性质及线段垂直平分线的性质作图即可.作∠ABC的平分线与线段BD的垂直平分线交于点P，则△PBD为所求作的等腰三角形．作∠ABC的平分线与线段BD的垂直平分线交于点P，则△PBD为所求作的等腰三角形．【解答】解：∵点P到∠ABC两边的距离相等，∴点P在∠ABC的平分线上，∵线段BD为等腰△PBD的底边，∴PB=PD，∴点P在线段BD的垂直平分线上，∴点P是∠ABC的平分线与线段BD的垂直平分线的交点．17.【答案】解：(1)如图所示；(2)解：∵DC是∠ACB的平分线，∴∠BCD=∠ACD，∵DE⊥AC，BC⊥AC，∴DE//BC，∴∠EDC=∠BCD，∴∠ECD=∠EDC，∴DE=CE，∵DE//BC，∴△ADE∽△ABC，∴DEBC =AEAC，设DE=CE=x，则AE=6−x，∴x4=6−x6，解得：x=125，即DE=125，故答案为：12．5【解析】本题考查了角的平分线的性质，平行线的性质，等腰三角形的性质，相似三角形的判定和性质，基本作图，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．(1)以C为圆心，任意长为半径画弧，交BC，AC两点，再以这两点为圆心，大于这两点的线段的一半为半径画弧，过这两弧的交点与C在直线交AB于D即可，根据过直线外一点作已知直线的垂线的方法可作出垂线即可；(2)根据平行线的性质和角平分线的性质推出∠ECD=∠EDC，进而证得DE=CE，由DE//BC，推出△ADE∽△ABC，根据相似三角形的性质即可推得结论．。

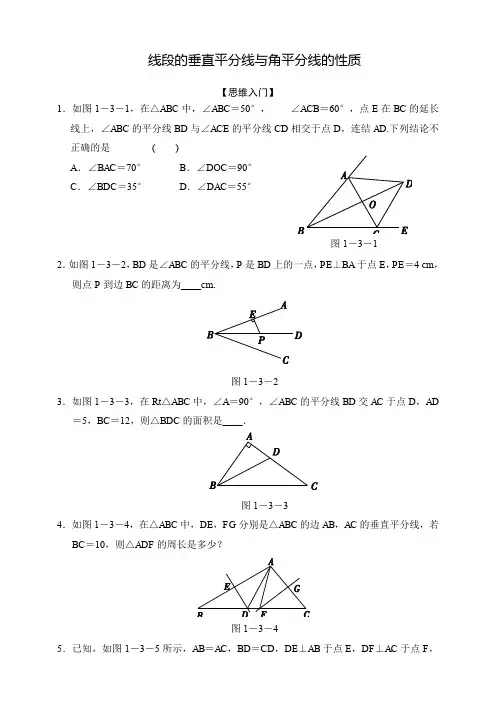
线段的垂直平分线与角平分线的性质【思维入门】1．如图1－3－1，在△ABC 中，∠ABC ＝50°， ∠ACB ＝60°，点E 在BC 的延长线上，∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ，连结AD .下列结论不正确的是( )A ．∠BAC ＝70°B ．∠DOC ＝90° C ．∠BDC ＝35°D ．∠DAC ＝55°2．如图1－3－2，BD 是∠ABC 的平分线，P 是BD 上的一点，PE ⊥BA 于点E ，PE ＝4 cm ，则点P 到边BC 的距离为____cm.图1－3－23．如图1－3－3，在Rt △ABC 中，∠A ＝90°，∠ABC 的平分线BD 交AC 于点D ，AD ＝5，BC ＝12，则△BDC 的面积是____．图1－3－34．如图1－3－4，在△ABC 中，DE ，FG 分别是△ABC 的边AB ，AC 的垂直平分线，若BC ＝10，则△ADF 的周长是多少？图1－3－45．已知，如图1－3－5所示，AB ＝AC ，BD ＝CD ，DE ⊥AB 于点E ，DF ⊥AC 于点F，求证：DE＝DF.【思维拓展】6．如图1－3－6，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，则AC的长是()5A．3 B．4C．6D．7．已知△ABC中，∠C＝90°，AD平分∠BAC交BC于D，若BC＝32，且BD∶CD＝9∶7，则D到AB的距离为()A．18 B．16 C．14 D．128．如图1－3－7，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有()A．1处B．2处C．3处D．4处Array 9．如图1－3－8，在△ABC中，∠C＝90°，AB＝10，AD是△ABC的一条角平分线．若CD＝3，则△ABD的面积为____．。

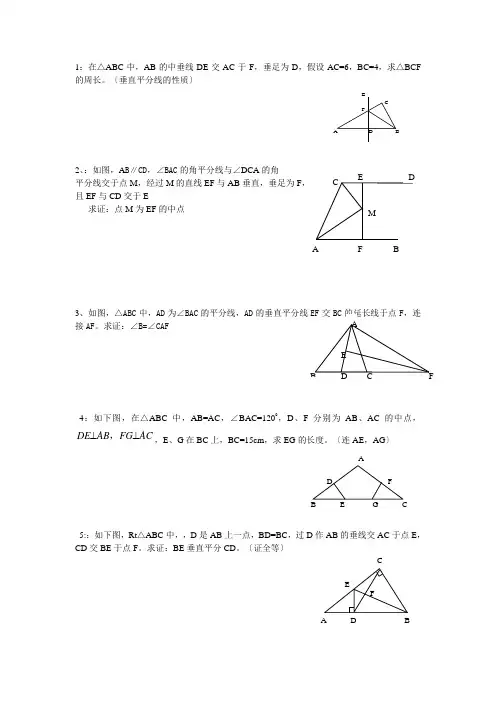
1：在△ABC 中，AB 的中垂线DE 交AC 于F ，垂足为D ，假设AC=6，BC=4，求△BCF 的周长。

〔垂直平分线的性质〕2、：如图，A B ∥CD ，∠BAC 的角平分线与∠DCA 的角平分线交于点M ，经过M 的直线EF 与AB 垂直，垂足为F且EF 与CD 交于E求证：点M 为EF 的中点3、如图，△ABC 中，AD 为∠BAC 的平分线，AD 接AF 。

求证：∠B=∠CAF4：如下图，在△ABC 中，AB=AC ，∠BAC=1200，D 、F 分别为AB 、AC 的中点，DE AB FG AC ⊥⊥，，E 、G 在BC 上，BC=15cm ，求EG 的长度。

〔连AE ，AG 〕A5:：如下图，Rt △ABC 中，，D 是AB 上一点，BD=BC ，过D 作AB 的垂线交AC 于点E ，CD 交BE 于点F 。

求证：BE 垂直平分CD 。

〔证全等〕CEA D BF1．如图，∠A ＝520，O 是AB 、AC 的垂直平分线的交点，那么∠OCB ＝ 。

2．如图，AB ＝AC ，∠A ＝440，AB 的垂直平分线MN 交AC 于点D ，那么∠DBC ＝ 。

3．如图，在△ABC 中，∠C ＝900，∠B ＝150，AB 的中垂线DE 交BC 于D 点，E 为垂足，假设BD ＝8，那么AC ＝ 。

4．如图，在△ABC 中，AB ＝AC ，DE 是AB 的垂直平分线，△BCE 的周长为24，BC ＝10，那么AB ＝ 。

5．如图，EG 、FG 分别是∠MEF 和∠NFE 的角平分线，交点是G ， BP 、CP 分别是∠MBC 和∠NCB 的角平分线，交点是P ，F 、C 在 AN 上，B 、E 在AM 上，假设∠G ＝680，那么∠P ＝ 。

6．如图，O 为∠A 与∠C 的平分线的交点，OE ⊥AC 于E ，假设OE=2那么点O 到AB 的距离与O 到CD 的距离的 和是＿＿＿＿＿；7．如图，在△ABC中，∠C=090，点E 为BC 上一点，ED ⊥AB 于D ，并且ED=EC ，AE=BE ，那么∠EAC 与∠B 的大小关系是＿＿＿＿＿8．如图，∠BAC=090 ，PM 、QN 分别垂直平分AB 、AC ，垂足分别为M 、N ，交BC 于P 、Q ，那么∠PAQ=＿＿＿＿〔用含α的式子表示〕9．如图在△ABC 中，∠BAC=072，∠B=068，AB 、AC 的垂直平分线分别交BC 于D 、E ，求∠EAD 的度数。

1.4 角平分线同步培优练习题一．选择题（共10小题）1．如图，已知点O为△ABC的两条角平分线的交点，过点O作OD⊥BC，垂足为D，且OD＝4．若△ABC的面积是34，则△ABC的周长为（）A．8.5B．15C．17D．342．如图，在△ABC中，∠C＝90°，AD是△ABC的一条角平分线．若AC＝6，AB＝10，则点D到AB边的距离为（）A．2B．2.5C．3D．43．如图，△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P，若点P 到直线AC的距离为4，则点P到直线AB的距离为（）A．4B．3C．2D．14．如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，AB＝20，CD＝6，若∠C＝90°，则△ABD面积是（）A．120B．80C．60D．405．如图，BP为∠ABC的平分线，过点D作BC、BA的垂线，垂足分别为E、F，则下列结论中错误的是（）A．∠DBE＝∠DBF B．DE＝DF C．2DF＝DB D．∠BDE＝∠BDF 6．如图，PM＝PN，∠BOC＝30°，则∠AOB的度数（）A．30°B．45°C．60°D．50°7．如图，Rt△ABC中，∠C＝90°，用尺规作图法作出射线AE，AE交BC于点D，CD＝2，P为AB上一动点，则PD的最小值为（）A．2B．3C．4D．无法确定8．在△ABC内部取一点P，使得点P到△ABC的三边距离相等，则点P是△ABC的（）A．三条高的交点B．三条角平分线的交点C．三条中线的交点D．三边的垂直平分线的交点9．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DE＝2，AC＝3，则△ADC 的面积是（）A．3B．4C．5D．610．如图所示，△ABC的两条外角平分线AP、CP相交于点P，PH⊥AC于H．若∠ABC＝60°，则下面的结论：①∠ABP＝30°；②∠APC＝60°；③PB＝2PH；④∠APH＝∠BPC，其中正确结论的个数是（）A．1个B．2个C．3个D．4个二．填空题（共5小题）11．如图，点O在△ABC内部，且到三边的距离相等．若∠BOC＝130°，则∠A＝．12．如图，已知△ABC的周长是20，OB、OC分别平分∠ABC和∠ACB，OD⊥BC于D，若△ABC的面积是30，则OD＝．13．如图，∠AOP＝∠BOP，PC∥OA，PD⊥OA，若∠AOB＝45°，PC＝6，则PD的长为．14．如图，AB∥CD，点P到AB，BC，CD距离都相等，则∠P＝度．15．如图，在△ABC中，∠C＝90°，AB＝10，AC＝6，角平分线AE与BF相交于点O，则点O到斜边AB的距离为．三．解答题（共7小题）16．在△ABC中，已知∠A＝90°，AB＝AC，BD平分∠ABC，DE⊥BC于E，请解答下列问题：（1）若AD＝2cm，则D点到BC边的距离是．（2）若BC＝7cm，则△CDE的周长为．（3）连接AE，试判断线段AE与BD的位置关系，并说明理由．17．已知：如图，△ABC的角平分线BE、CF相交于点P．求证：点P在∠A的平分线上．18．在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，BD：DC＝2：1，BC＝7.8cm，求点D到AB的距离．19．已知，如图，∠C＝90°，∠B＝30°，AD是△ABC的角平分线．（1）求证：BD＝2CD；（2）若CD＝2，求△ABD的面积．20．如图：已知OA和OB两条公路，以及C、D两个村庄，建立一个车站P，使车站到两个村庄距离相等即PC＝PD，且P到OA，OB两条公路的距离相等．21．在四边形ABCD中，CE平分∠BCD交AD于点E，点F在线段CE上运动．（1）如图1，已知∠A＝∠D＝90°①若BF平分∠ABC，则∠BFC＝°②若∠BFC＝90°，试说明∠DEC＝∠ABC；（2）如图2，已知∠A＝∠D＝∠BFC，试说明BF平分∠ABC．22．证明命题“角平分线上的点到角两边的距离相等”，要根据题意，画出图形，并用符号表示已知求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．（1）已知：如图，OC是∠AOB的角平分线，点P在OC上，，．求证：．（请你补全已知和求证）（2）写出证明过程．参考答案一．选择题（共10小题）1．【分析】根据角平分线的性质得到点O到△ABC各边的距离为4，利用三角形面积公式得到×AB×4+×AC×4+×BC×4＝34，然后计算出AB+AC+BC即可．【解答】解：∵点O为△ABC的两条角平分线的交点，∴点O到△ABC各边的距离相等，而OD⊥BC，OD＝4，∴点O到△ABC各边的距离为4，∵S△ABC＝S△AOB+S△BOC+S△AOC，∴×AB×4+×AC×4+×BC×4＝34，∴AB+AC+BC＝17，即△ABC的周长为17．故选：C．2．【分析】作DE⊥AB于E，如图，先根据勾股定理计算出BC＝8，再利用角平分线的性质得到DE＝DC，设DE＝DC＝x，利用面积法得到10x＝6（8﹣x），然后解方程即可．【解答】解：作DE⊥AB于E，如图，在Rt△ABC中，BC＝＝8，∵AD是△ABC的一条角平分线，DC⊥AC，DE⊥AB，∴DE＝DC，设DE＝DC＝x，S△ABD＝DE•AB＝AC•BD，即10x＝6（8﹣x），解得x＝3，即点D到AB边的距离为3．故选：C．3．【分析】过点P作PF⊥AC于F，作PG⊥BC于G，PH⊥AB于H，然后根据角平分线上的点到角的两边的距离相等即可得解．【解答】解：如图，过点P作PF⊥AC于F，作PG⊥BC于G，PH⊥AB于H，∵BD、CE是△ABC的外角平分线，∴PF＝PG，PG＝PH，∴PF＝PG＝PH，∵点P到AC的距离为4，∴PH＝4，即点P到AB的距离为4．故选：A．4．【分析】根据角平分线的性质得出DE＝CD＝6，进而利用三角形的面积公式解答即可．【解答】解：∵AD是△ABC的角平分线，DE⊥AB，∠C＝90°，∴CD＝DE＝6，∴△ABD面积＝，故选：C．5．【分析】根据角平分线的性质、全等三角形的判定定理和性质定理判断即可．【解答】解：∵BP为∠ABC的平分线，DE⊥AC，DF⊥AB，∴DE＝DF，B正确，不符合题意；在Rt△DBE和Rt△DBF中，，∴Rt△DBE≌Rt△DBF，∴∠DBE＝∠DBF，∠BDE＝∠BDF，A、D正确，不符合题意，2DF不一定等于DB，C错误，符合题意，故选：C．6．【分析】由角平分线性质定理的逆定理和角的和差直接求出∠AOB的度数为60°．【解答】解：如图所示：∵点P在∠AOB的内部，PM⊥AO，PN⊥OB，PM＝PN，∴点P在∠AOB的角平分线上，∴OC平分∠AOB，∵∠BOC＝30°，∴∠AOB＝60°，故选：C．7．【分析】当DP⊥AB时，根据垂线段最短可知，此时DP的值最小．再根据角平分线的性质定理可得DP＝CD解决问题；【解答】解：当DP⊥AB时，根据垂线段最短可知，此时DP的值最小．由作图可知：AE平分∠BAC，∵DC⊥AC，DP⊥AB，∴DP＝CD＝2，∴PD的最小值为2，故选：A．8．【分析】根据角平分线的性质解答．【解答】解：∵角的平分线上的点到角的两边的距离相等，∴点P到△ABC的三边距离相等，则点P是△ABC的三条角平分线的交点，故选：B．9．【分析】过点D作DF⊥AC于F，根据角平分线上的点到角的两边距离相等可得DE＝DF，再根据（1）中所求S△ACD＝3列出方程求解即可．【解答】解：如图，过点D作DF⊥AC于F，∵AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，∴DE＝DF＝2．∴S△ACD＝AC•DF＝×3×2＝3，故选：A．10．【分析】如图作，PM⊥BC于M，PN⊥BA于N．利用角平分线的判定定理和性质定理可得PB是∠ABC的平分线，由△P AN≌△P AH，△PCM≌△PCH，推出∠APN＝∠APH，∠CPM＝∠CPH，由∠MPN＝180°﹣∠ABC＝120°，推出∠APC＝∠MPN＝60°，由∠BPN＝∠CP A＝60°，推出∠CPB＝∠APN＝∠APH即可一一判断．【解答】解：如图作，PM⊥BC于M，PN⊥BA于N．∵∠P AH＝∠P AN，PN⊥AD，PH⊥AC，∴PN＝PH，同理PM＝PH，∴PN＝PM，∴PB平分∠ABC，∴∠ABP＝∠ABC＝30°，故①正确，∵在Rt△P AH和Rt△P AN中，，∴△P AN≌△P AH，同理可证，△PCM≌△PCH，∴∠APN＝∠APH，∠CPM＝∠CPH，∵∠MPN＝180°﹣∠ABC＝120°，∴∠APC＝∠MPN＝60°，故②正确，在Rt△PBN中，∵∠PBN＝30°，∴PB＝2PN＝2PH，故③正确，∵∠BPN＝∠CP A＝60°，∴∠CPB＝∠APN＝∠APH，故④正确．二．填空题（共5小题）11．【分析】由条件可知BO、CO平分∠ABC和∠ACB，利用三角形内角和可求得∠A．【解答】解：∵点O到△ABC三边的距离相等，∴BO平分∠ABC，CO平分∠ACB，∴∠A＝180°﹣（∠ABC+∠ACB）＝180°﹣2（∠OBC+∠OCB）＝180°﹣2×（180°﹣∠BOC）＝180°﹣2×（180°﹣130°）＝80°，故答案为：80°．12．【分析】根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等（即OE＝OD＝OF），从而可得到△ABC的面积等于周长的一半乘以3，代入求出即可．【解答】解：如图，连接OA，过O作OE⊥AB于E，OF⊥AC于F，∵OB、OC分别平分∠ABC和∠ACB，∴OE＝OF＝OD，∵△ABC的周长是20，OD⊥BC于D，∴S△ABC＝×AB×OE+×BC×OD+×AC×OF＝×（AB+BC+AC）×OD＝×20×OD＝30，解得：OD＝3，故答案为：313．【分析】过P作PE⊥OB，根据角平分线的定义和平行线的性质易证得△PCE是等腰直角三角形，得出PE＝3，根据角平分线的性质即可证得PD＝PE＝3．【解答】解：过P作PE⊥OB，∵∠AOP＝∠BOP，∠AOB＝45°，∴∠AOP＝∠BOP＝22.5°，∵PC∥OA，∴∠OPC＝∠AOP＝22.5°，∴∠PCE＝45°，∴△PCE是等腰直角三角形，∴PE＝PC＝×6＝3，∵∠AOP＝∠BOP，PD⊥OA，PE⊥OB，∴PD＝PE＝3，故答案为3．14．【分析】根据到角的两边距离相等的点在角的平分线上可得BP、CP分别是∠ABC和∠BCD的平分线，再根据两直线平行，同旁内角互补和角平分线的定义解答即可．【解答】解：∵点P到AB、BC、CD距离都相等，∴BP、CP分别是∠ABC和∠BCD的平分线，∴∠CBP＝∠ABC，∠BCP＝∠BCD，∴∠CBP+∠BCP＝（∠ABC+∠BCD），∵AB∥CD，∴∠ABC+∠BCD＝180°，∴∠CBP+∠BCP＝×180°＝90°，∴∠P＝180°﹣（∠CBP+∠BCP）＝180°﹣90°＝90°．故答案为：9015．【分析】利用勾股定理列式求出BC，根据角平分线上的点到角的两边距离相等可得点O 到△ABC三边的距离相等，设为h，再利用△ABC的面积列出方程求解即可．【解答】解：∵∠C＝90°，AB＝10，AC＝6，∴BC＝＝＝8，∵角平分线AE与BF相交于点O，∴点O到△ABC三边的距离相等，设为h，则S△ABC＝（10+6+8）h＝×6×8，解得h＝2，即点O到斜边AB的距离为2．故答案为：2．三．解答题（共7小题）16．【分析】（1）根据角平分线的性质定理解答；（2）证明△ABD≌△EBD，得到BA＝BE，根据三角形的周长公式计算即可；（3）根据线段垂直平分线的判定定理解答．【解答】解：（1）∵BD平分∠ABC，DE⊥BC，∠A＝90°，∴DE＝AD＝2cm，故答案为：2cm；（2）在△ABD和△EBD中，，∴△ABD≌△EBD，∴BA＝BE，△CDE的周长＝CD+CE+DE＝CD+AD+CE＝AC+CE＝AB+CE＝BE+CE＝BC＝7cm，故答案为：7cm；（3）∵DA＝DE，BA＝BE，∴BD⊥AE．17．【分析】过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N，根据角平分线上的点到角的两边距离相等可得PD＝PM，同理可得PM＝PN，从而得到PD＝PN，再根据到角的两边距离相等的点在角的平分线上证明即可．【解答】证明：如图，过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N，∵BE平分∠ABC，点P在BE上，∴PD＝PM，同理，PM＝PN，∴PD＝PN，∴点P在∠A的平分线上．18．【分析】先要过D作出垂线段DE，根据角平分线的性质求出CD＝DE，再根据已知即可求得D到AB的距离的大小．【解答】解：过点D作DE⊥AB于E．∵AD平分∠BAC，DE⊥AB，DC⊥AC∴CD＝DE又BD：DC＝2：1，BC＝7.8cm∴DC＝7.8÷（2+1）＝7.8÷3＝2.6cm．∴DE＝DC＝2.6cm．∴点D到AB的距离为2.6cm．19．【分析】（1）过D作DE⊥AB于E，依据角平分线的性质，即可得到DE＝CD，再根据含30°角的直角三角形的性质，即可得出结论；（2）依据AD＝BD＝2CD＝4，即可得到Rt△ACD中，AC＝＝2，再根据△ABD的面积＝×BD×AC进行计算即可．【解答】解：（1）如图，过D作DE⊥AB于E，∵∠C＝90°，AD是△ABC的角平分线，∴DE＝CD，又∵∠B＝30°，∴Rt△BDE中，DE＝BD，∴BD＝2DE＝2CD；（2）∵∠C＝90°，∠B＝30°，AD是△ABC的角平分线，∴∠BAD＝∠B＝30°，∴AD＝BD＝2CD＝4，∴Rt△ACD中，AC＝＝2，∴△ABD的面积为×BD×AC＝×4×2＝4．20．【分析】作∠AOB的角平分线和线段CD的垂直平分线，它们的交点为P点．【解答】解：如图，点P为所作．21．【分析】（1）①先根据∠A+∠D＝180°得AB∥CD，可得∠ABC+∠BCD＝180°，根据角平分线和三角形的内角和可得结论；②先根据同角的余角可得：∠CBF＝∠DEC，由①知：AB∥CD，可得结论；（2）如图2，延长BF交于点M，根据四边形的内角和定理和邻补角的性质可得∠DCF ＝∠EMF，根据三角形的内角和定理得∠FEM＝∠CBF，同理得∠FEM＝∠ABF，从而得结论．【解答】解：（1）①∵∠A＝∠D＝90°，∴∠A+∠D＝180°，∴AB∥CD，∴∠ABC+∠BCD＝180°，∵CE平分∠BCD，BF平分∠ABC，∴∠CBF＝，∠BCF＝，∴∠CBF+∠BCF＝＝90°，∴∠BFC＝90°；故答案为：90②∵∠BFC＝90°，∴∠CBF+∠BCF＝90°，∵∠D＝90°，∴∠DCE+∠DEC＝90°，∵CE平分∠BCD，∴∠DCE＝∠BCF，∴∠CBF＝∠DEC，由①知：AB∥CD，∴∠ABC+∠BCD＝180°，∴∠CBF＝∠ABC，∴∠DEC＝∠ABC；（2）如图2，延长BF交于点M，∵∠BFC＝∠D，∠BFC+∠CFM＝180°，∴∠CFM+∠D＝180°，∴∠FMD+∠DCF＝180°，∵∠FMD+∠EMF＝180°，∴∠DCF＝∠EMF，∵CE平分∠BCD，∴∠DCF＝∠BCF，∴∠BCF＝∠EMF，∵∠EFM＝∠BFC，∴∠FEM＝∠CBF，∵∠CFB＝∠A，同理得∠FEM＝∠ABF，∴∠ABF＝∠CBF∴BF平分∠ABC．22．【分析】（1）根据题意、结合图形写出已知和求证；（2）证明△OPD≌△OPE，根据全等三角形的性质证明结论．【解答】解：（1）已知：如图，OC是∠AOB的角平分线，点P在OC上，PD⊥OA于D，PE⊥OB于E，求证：PD＝PE，故答案为：PD⊥OA于D；PE⊥OB于E；PD＝PE；（2）证明：在△OPD和△OPE中，，∴△OPD≌△OPE（AAS）∴PD＝PE．。

八下数学专题之垂直平分线和角平分线训练题（人教版）一．选择题（共6小题）1．到三角形三个顶点的距离都相等的点是（）A．两条中线的交点B．两条高的交点C．两条角平线的交点D．两条边的垂直平分线的交点2．如图，在△ABC中，AB的垂直平分线分别交AB，BC于点D，E，AC的垂直平分线分别交AC，BC于点F，G，且△AEG的周长是20，则线段BC的长为（）A．40B．20C．15D．103．在△ABC中，AB＝5，BC＝6，AC＝3，BC的垂直平分线交AB于点E，交BC于点D，连接CE，则△ACE的周长为（）A．8B．9C．10D．114．如图，OC平分∠AOB，点P是射线OC上一点，PM⊥OB于点M，点N是射线OA上的一个动点．若PM＝4，则PN的长度不可能是（）A．3B．4C．5D．65．如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为13cm，则△ABC的周长为（）cmA．13B．16C．19D．216．如图，OC平分∠AOB，CP⊥OB于点P，CP＝3，点Q在OA上，OQ＝6，则△OCQ的面积为（）A．B．6C．9D．18二．填空题（共6小题）7．如图，DE为△ABC的边BC的垂直平分线，交AB于点D，交BC于点E，且∠B＝35°，∠A＝65°，则∠ACD的度数为．8．如图，在△ABC中，DE垂直平分BC交A于点D，交BC于点E．若AB＝10cm，AC＝8cm，则△ACD的周长是cm．9．如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，连接AD，若BD＝3CD，则S△AED：S△ABC＝．10．如图，△ABC中，AB的垂直平分线交AC于D，已知AC＝10cm，BC＝7cm，则△BCD 的周长是．11．如图，在△ABC中，∠BAC和∠ABC的平分线AE，BF相交于点O，AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，若AB＝8，OD＝1，则△AOB的面积为．12．如图，CO、BO是△ABC的两个外角∠PCB、∠QBC的角平分线，OM⊥AP，ON⊥AQ，且OM＝ON．下列结论中正确的个数有个．①∠P AO＝∠QAO；②∠AOB＝∠ACB；③2∠COB＝180°+∠CAB；④∠P AQ+2∠COB＝180°．三．解答题（共3小题）13．如图，在△ABC中，AB＝13，AC＝12，BC＝5，DE是AB的垂直平分线，DE分别交AC，AB于点E，D．求AE的长．14．如图，在△ABC中，∠ACB、∠ABC的平分线l1、l2相交于点O．（1）求证：点O在∠BAC的平分线上；（2）连接OA，若AB＝AC＝5，BO＝4，AO＝2，则点O到三角形三条边的距离是．15．如图，在△ABC中，AD⊥BC，垂足为D，BD＝CD，延长BC至E，使得CE＝CA，连接AE．（1）求证：∠B＝∠ACB．（2）若AB＝5，AD＝4，①求△ABC的面积．②求△ABE的周长．。

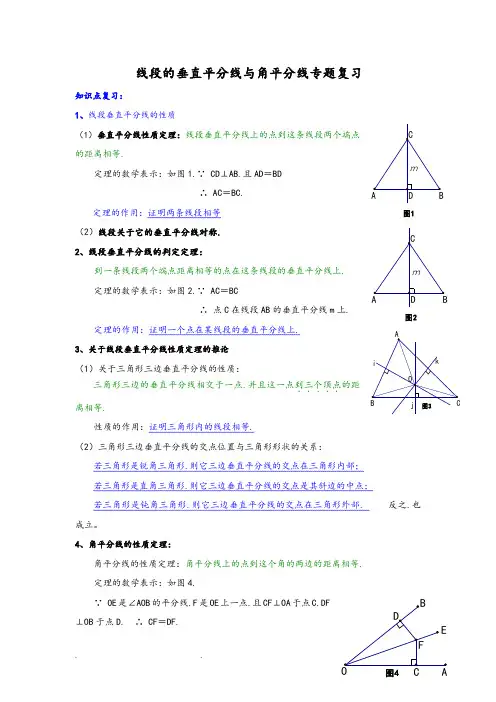
线段的垂直平分线与角平分线专题复习知识点复习：1、线段垂直平分线的性质（1）垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示：如图1.∵ CD ⊥AB.且AD ＝BD∴ AC ＝BC.定理的作用：证明两条线段相等 （2）线段关于它的垂直平分线对称.2、线段垂直平分线的判定定理：到一条线段两个端点距离相等的点在这条线段的垂直平分线上. 定理的数学表示：如图2.∵ AC ＝BC∴ 点C 在线段AB 的垂直平分线m 上.定理的作用：证明一个点在某线段的垂直平分线上.3、关于线段垂直平分线性质定理的推论（1）关于三角形三边垂直平分线的性质：三角形三边的垂直平分线相交于一点.并且这一点到三个顶点．．．．．的距离相等.性质的作用：证明三角形内的线段相等.（2）三角形三边垂直平分线的交点位置与三角形形状的关系：若三角形是锐角三角形.则它三边垂直平分线的交点在三角形内部；若三角形是直角三角形.则它三边垂直平分线的交点是其斜边的中点；若三角形是钝角三角形.则它三边垂直平分线的交点在三角形外部. 反之.也成立。

4、角平分线的性质定理：角平分线的性质定理：角平分线上的点到这个角的两边的距离相等. 定理的数学表示：如图4.∵ OE 是∠AOB 的平分线.F 是OE 上一点.且CF ⊥OA 于点C.DF ⊥OB 于点D. ∴ CF ＝DF.图1图2定理的作用：①证明两条线段相等；②用于几何作图问题； 角是一个轴对称图形.它的对称轴是角平分线所在的直线.5、角平分线性质定理的逆定理：角平分线的判定定理：在角的内部到角的两边距离相等的点在这个角的角平分线上.定理的数学表示：如图5.∵点P 在∠AOB 的内部.且PC ⊥OA 于C.PD ⊥OB 于D.且PC ＝PD. ∴点P 在∠AOB 的平分线上.定理的作用：用于证明两个角相等或证明一条射线是一个角的角平分线6、关于三角形三条角平分线的定理：（1）关于三角形三条角平分线交点的定理：三角形三条角平分线相交于一点.并且这一点到三边的距离相等.定理的数学表示：如图6.如果AP 、BQ 、CR 分别是△ABC 的内角∠BAC 、 ∠ABC 、∠ACB 的平分线.那么：① AP 、BQ 、CR 相交于一点I ；② 若ID 、IE 、IF 分别垂直于BC 、CA 、AB 于点D 、E 、F.则DI ＝EI ＝FI. 定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题. （2）三角形三条角平分线的交点位置与三角形形状的关系：三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心（即内切圆的圆心）.7、关于线段的垂直平分线和角平分线的作图：（1）会作已知线段的垂直平分线； （2）会作已知角的角平分线； （3）会作与线段垂直平分线和角平分线有关的简单综合问题的图形.精品习题：1．在△ABC 中.∠C=90º.BD 是∠ABC 的平分线.已知.AC=32.且AD ：DC=5：3.则点D 到AB 的距离为_______.2．如图.在△ABD 中.AD=4.AB=3.AC 平分∠BAD.则:ABC ACD S S ∆∆= （ ） A ．3:4 B ．4:3 C ．16:19 D ．不能确定3．如图.ΔABC的三边AB、BC、CA的长分别是20、30、40、其中三条角平分线将ΔABD分为三个三角形.则SABO∆：SBCO∆：SCAO∆等于______.4．如图所示.∠BAC＝105°.若MP和NQ分别垂直平分AB和AC．则∠PAQ的度数为．5．AD∥BC.∠D=90︒.AP平分∠DAB.PB平分∠ABC.点P恰好在CD上.则PD与PC的关系是（）A．PD>PC B．PD<PC C．PD=PC D．无法判断6．如图.有A、B、C三个居民小区的位置成三角形.现决定在三个小区之间修一个超市.使超市到三个小区的距离相等.则超市应建在( )A．在AC、BC两边高线的交点处B.在AC、BC两边中线的交点处C．在AC、BC两边垂直平分线的交点处D.在∠A、∠B的角平分线的交点处7．如图.CD是Rt△ABC斜边AB上的高.将△BCD沿CD折叠.B点恰好落在AB的中点E处.则∠A等于( )A．25º B.30º C.45º D.60º8．AC=AD.BC=BD.则有（）A．AB垂直平分CD B．CD垂直平分ABC．AB与CD互相垂直平分D．CD平分∠ACB9．如图.OP平分∠AOB.PA⊥OA.PB⊥OB.垂足分别为A.B．下列结论中不一定成立的是（）A．PA=PB B．PO平分∠APB C．OA=OB D．AB垂直平分OP10．随着人们生活水平的不断提高.汽车逐步进入到千家万户.小红的爸爸想在本镇的三条相互交叉的公路（如图所示）.建一个加油站.要求它到三条公路的距离相等.这样可供选择的地址有（）处。

第2讲垂直平分线1.垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等PD为线段AB的垂直平分线，必然需要连接PA、PB,构造出等腰△ PAB,进而求解. 逆定理：若PA=PB，则点P在AB的垂直平分线上.【例题讲解】例题1、如图，在△ ABC中，点D、E、F分别在BC、AB、AC上.BD=CF, BE=CD , DG丄EF于点G,且EG=FG.求证：AB=AC.【分析】可知GD为EF的垂直平分线，遇见垂直平分线，必然要将垂直平分线上的点与线段两端点连接【解答】解：连接DE、DF如右图所示Q DG EF,EG FGDE DFBD CF在厶BDE和厶CFD中，BE CDDE DFBDE CFDB CAB AC .例题2、如图，在Rt A ABC 中，/ C=90°,点 D 在BC 上，点E在AB 上，且DE // AC, AE=5, DE=2,DC=3，动点P从点A出发，沿边AC以每秒2个单位长的速度向终点C运动，设运动时间为t秒。

(1) ______________________ 线段AC的长= ;(2) 在线段EA上有一点Q,满足ED=EQ，连接DQ、PE,当PE丄DQ时，求出t的值.【解答】(1)AC=6;(2)当PE丄DQ时，由于ED=EQ，易证PE垂直平分DQ , 所以连接PD、PQ,只需使PD=PQ即可可知AP=2t，所以PC=6-2t；CD=3, EQ=2，所以AQ=3,所以AF 4AQ12QF3AQ9555512所以PF 2t —5在Rt A PCD 中，PD2=32+ ( 6-2 t) 2;22 c在Rt A PQF 中，PQ2=2t1295522所以32+ (6-21) 2= 2t129，解得t5~552【总结】遇见垂直平分线，连接垂直平分线上的点与线段两端点是必然的！【最好方法】当PE丄DQ时，易证PE平分/ DEA ,由【角平分线模型三】可知，平行+角平分线=等腰三角形，所以△ AEP为等腰三角形，所以AP=AE=5,即2t=5,【巩固练习】1、三角形三条边的垂直平分线的交点是三角形的( : )A.重心B.内心C.外心D.中心2、在厶AOB的内部有点P，点P与P1关于OA对称，点P与P2关于BO对称，①则△ OP1P2是( )A.等边三角形B.等腰三角形C.直角三角形D.钝角三角形②当/ AOB满足什么条件时，△ OP1P2是等边三角形？3、如图，△ ABC中，AB, AC的垂直平分线交BC于D、E,(1)若/ BAC=100°,则/ DAE= _________ ;(2)_______________________________ 若/ BAC=80°,则/ DAE= ;(3)_______________________________ 若/ DAE=10°,则/ BAC= ;(4)若厶ABC的周长为20,A ADE的周长为12,贝U AB+AC= _________ ;(5)当AB=AC，且/ BAC=120°,则厶ADE为何种特殊三角形？4、如图，等边△ ABC的边长为3, BO、CO分别为/ ABC、/ ACB的角平分线，BO、CO的垂直平分线交BC于E、F，则EF的长为5、如图，已知等腰△ ABC, AB=BC=5, AC= 10 ,在BC边上存在一点P,恰好在线段AB的垂直平分线上，贝U BP的长为6、如图所示，已知AD是厶ABC的角平分线，DE丄AB, DF丄AC,垂足分别是E, F.求证：AD垂直平分EF.7、A ABC中，D为BC中点，DE丄BC,交/ BAC的平分线于点E, EF丄AB于F, EG丄AC于G.求证: BF=CG.8、如图，△ ABC中，点D在BC上，且AD的垂直平分线EF交BC延长线于点F，若/ FAC = Z B,求证: AD 平分/ BAC.9、如图，在△ ABC 中，AB=AC , D 为三角形内一点，且△ DBC 为等边三角形• (1) 求证：直线AD 垂直平分BC ;(2) 以AB 为一边，在 AB 的右侧画等边△ ABE ，连接DE ，试判断以DA 、DB 、DE 三条线段是否能构成 直角三角形？请说明理由•_ 210、已知二次函数y=ax+2ax+c 的图象与x 轴分别交于A 、B 两点(点A 在点B 的左侧)，与y 轴交于点C , 顶点为P ,若C ( 0, 2), BC 的垂直平分线过点 A ，求这个二次函数的关系式. 4y= x+4与x 轴交于点A ,与y 轴交于点B ，点P 从点O 出发沿3OA 以每秒1个单位长的速度向点 A 匀速运动，到达点 A 后立刻以原来的速度沿 AO 返回；点Q 从A 出发 沿AB 以每秒1个单位长的速度向点 B 匀速运动，当点 P 、Q 运动时，DE 保持垂直平分 PQ ，且交PQ 于 点D ，交折线QB- BO- OP 于点E.点P 、Q 同时出发，当点 Q 到达点B 时停止运动，点 P 也随之停止，设 点P 、Q 运动的时间为t 秒(t>0). (1) ______________________ 点Q 的坐标是( , )(用含t 的代数式表示)； (2) 当t 为何值时，直线 DE 经过点O.12、如图1,在矩形 ABCD 中，AB=4, BC=3，点E 是射线 CD 上的一个动点，把△ BCE 沿BE 折叠，点C 的对应点为F.(1) 若点F 刚好落在线段 AD 的垂直平分线上时，求线段 CE 的长; (2) 若点F 刚好落在线段 AB 的垂直平分线上时，求线段 CE 的长; (3)当射线AF 交线段CD 于点G 时，请直接写出 CG 的最大值.11、如图，在平面直角坐标系中，直线*用1913、如图，二次函数的图象与x轴相交于点A (-3 , 0)、B (-1 , 0),与y轴相交于点C ( 0, 3)，点P是该图象上的动点，点Q的坐标为(4, 0).(1) 求该二次函数的表达式；(2) 当OP〃CQ时，求点P的坐标;(3) 点M , N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M , N中有一点到达Q点时，两点同时停止运动.设运动时间为t秒，当直线PQ垂直平分线段MN时，请求出此时t的值及点P的坐标.214、已知抛物线y=ax+bx+c (a<0)与x轴交于点A (8, 0)和B (一12, 0)，与y轴交于点C (0, 6).(1)求该抛物线的解析式；(2)点D在线段AB上且AD=AC，若动点M从A出发沿线段AB以每秒1个单位长度的速度匀速运动，同时另一动点N以某一速度从B出发沿线段BC匀速运动，问是否存在某一时刻t (秒)，使线段MN被直线CD垂直平分？若存在，请求出此时的时间t和点N的运动速度；若不存在，请说明理由；参考答案1. 答案： B2. 答案：① B ;②Z AOB= 30°3.答案： (1) 20°;( 2) 20°;( 3) 95°; (4) 8;( 5)等边三角形4. 答案： 15.答案： 25 86.证明： QAD 是厶ABC 的角平分线，DE 丄AB ， DF 丄AC ， DE=DF在 Rt A ADE 和 Rt A ADF 中, AD=AD ，DE=DF ， Rt A ADE 也R A ADF( HL)， AE = AF ，又 DE = DF ，AD 垂直平分EF (到线段两端点的距离相等的点一定在线段的垂直平分线上 )7.证明：如图，连接 BE 、BC ， QED 丄BC ，D 为BC 中点 BE= ECQEF 丄 AB ，EG 丄 AG ，且 AB 平分/ FAG FE=EG在厶 BFE 禾口 Rt A CGE 中，BE=CE ，EF=EG ， Rt △ BFE 也 Rt A CGE(HL)， BF=CG. 8.证明：QEF 是AD 的垂直平分线， AF=DF/ EAF = Z EDF ，Q / EAF = Z FAC + Z CAD ，/ EDF = Z BAD+Z B ， 又Q Z FAC =Z BZ BAD = Z CAD ，即AD 平分Z BAC. 9.答案：(1) Q △ DBC 为等边三角形，DB=DC ， D 在BC 的垂直平分线上QAB = AC ， A 在BC 的垂直平分线上， 直线AD 垂直平分BC ;(2)以DA ，DB ，DE 三条线段能构成直角三角形； 理由：连接CE ，Q Z ABD = Z ABE- Z DBE= 60°- Z DBE= Z DBC - Z DBE= Z EBC，在厶 EBC 和厶 ABD 中，AB=EB ，/ ABD = Z EBC , DB=CB , △ EBC ◎△ ABD ( SAS ),/ BCE = Z ADB , AD = CE.在厶 ADB 和厶 ADC 中, AD=AD , AB =AC , DB=DC , △ ADB ◎△ ADC (SSS ,/ ADB = Z ADC ,1/ ADB =丄(360 ° - / BCD )= 150 °2/ BCE = Z BDA = 150°,/ DCE = Z BCE- / BCD= 150° -60 ° =90° QCE = DA , DC = DB ,以DA , DB , DE 三条线段能构成直角三角形 10. 解：QBC 的垂直平分线过点 A ,此时/ AQP = 90 ° . 由厶APQ 〜△ ABO 得竺AO1 3.解得t -； 3 5 8如图3，当PQ // BO 时，QDE 丄PQ , DE 丄BO ,四边形 QBED 是直角梯形. 此时/ APQ = 90 ° .由厶AQP~ △ ABO ，得 锂 塑.2a 2a设 AB AC 2m ,则AO m 1,BO m 1,QC 0,2 , CO2Q 在 Rt A AOC 中，2 2 AO CO AC 2, - 2 2 2 即 m 1 22 2m , 解得当m 1 时，A 0 ,0 ,B 2,0 ,C 0,2 （舍去）；当m -时，A 8 2 二,0 ,B 二,0 ,C 0,2，此时二次函数解析式为 y1_ 2 二次函数 y=ax +2ax+c 的对称轴为 x9x 2.4c 3 4 3 t, t ；5 5 四边形QBED 能成为直角梯形。

线段的垂直平分线和角平分线内容分析线段的垂直平分线和角平分线是八年级数学上学期第十九章第四节内容，主要对线段的垂直平分线和角平分线进行讲解，重点是线段的垂直平分线和角平分线定理的理解，难点是线段的垂直平分线和角平分线定理的运用．通过这节课的学习一方面为我们后期学习直角三角形提供依据，另一方面也为后面学习勾股定理奠定基础．知识结构模块一：线段的垂直平分线知识精讲一、线段的垂直平分线的性质及逆定理1、线段的垂直平分线上的任意一点到这条线段的两个端点的距离相等；注意：垂直平分线中的垂直是相互的，而平分则要看清楚到底是谁被平分．2、和一条线段两个端点距离相等的点，在这条线段的垂直平分线上．2 / 15【例1】 已知：如图，在ABC ∆中，90C ∠=°，30A ∠=︒，DE 垂直平分AB 于点D ，交AC于点E ．求证：DE CE =．【解析】连接BE∵DE 垂直平分AB 于点D ， ∴EB AE =， ∴︒=∠=∠30ABE A∵︒=∠+∠90ABC A ，30A ∠=︒， ∴︒=∠60ABC ，∴︒=∠30EBC ．可证BCE BDE ≌△△()S A A ..，则CE DE =．【总结】本题主要考查直角三角形的性质以及线段垂直平分线的性质．【例2】 已知：如图，在ABC ∆中，90ACB ∠=°，D 为BC 延长线上一点，E 是AB 上一点，EM 垂直平分BD M ，为垂足，DE 交AC 于点F ．求证：E 在AF 的垂直平分线上．【解析】∵EM 垂直平分BD ，∴ED EB =，∴D B ∠=∠∵90ACB ∠=°，∴︒=∠+∠90B A ，︒=∠+∠90DFC D ∴DFC A ∠=∠ ∵AFE DFC ∠=∠， ∴AFE A ∠=∠，∴EF AE = ∴E 在AF 的垂直平分线上．【总结】本题主要考查线段垂直平分线性质定理以及逆定理的运用．【例3】 如图，ABC ∆中，AD 是BAC ∠的平分线，点E 在BC 延长线上，且例题解析DEABCABACONNMGFEDC BABAE ACE ∠=∠．求证：点E 在AD 的垂直平分线上．【解析】∵AD 是BAC ∠的平分线，∴DAC BAD ∠=∠∵BAD DAE BAE ∠+∠=∠，DAC ADE ACE ∠+∠=∠，又BAE ACE ∠=∠ ∴DAE ADE ∠=∠ ∴ED EA =∴点E 在AD 的垂直平分线上．【总结】本题一方面考查三角形的外角性质，另一方面考查线段垂直平分线逆定理的运用．【例4】 已知：在ABC ∆中，90ACB ∠=，30A ∠=°，BD 平分B ∠交AC 于点D ．求证：点D 在AB 的垂直平分线上．【解析】∵︒=∠+∠90ABC A ，30A ∠=︒，∴︒=∠60ABC ，∵BD 平分B ∠，∴︒=∠30DBA ∴ABD A ∠=∠，∴BD AD = ∴点D 在AB 的垂直平分线上．【总结】本题一方面考查直角三角形的性质，另一方面考查线段垂直平分线逆定理的运用．【例5】 已知：在ABC 中，ON 是AB 的垂直平分线, OA OC =．求证：点O 在线段BC 的垂直平分线．【解析】∵ON 是AB 的垂直平分线, ∴OB OA =∵OA OC =，∴OC OB = ∴点O 在线段BC 的垂直平分线．【总结】本题主要考查线段垂直平分线性质定理以及逆定理的运用．【例6】 如图，在△ABC 中，∠A =30°，DE 垂直平分AB ，FM 垂直平分AD ，GN 垂直平分BD ．求证：AF = FG = BG ． 【答案】见解析【解析】∵DE 垂直平分AB ，4 / 15GF ECBAEDCBA∴︒=∠=∠30DAB A ∵FM 垂直平分AD ， ∴DF AF =， ∴FDA A ∠=∠，∴︒=∠+∠=∠60ADF A DFE 同理可得：︒=∠60DGB ， ∴DFG △是等边三角形， ∴BG FG DF ==又∵DF AF =，BG DG =， ∴AF = FG = BG ．【总结】本题主要考查等腰三角形的性质以及线段垂直平分线的性质．【例7】 如图，在△ABC 中，∠B =22.5°，边AB 的垂直平分线交BC 于点D ，DF ⊥AC ，并与BC 边上的高AE 交于点G ． 求证：EG = EC ． 【答案】见解析【解析】∵边AB 的垂直平分线交BC 于点D ，∴DA DB =，∴︒=∠=∠5.22B BAD ∴︒=∠+∠=∠45BAD B ADC ， ∴ADE △为等腰直角三角形， ∴AE DE =证得：()A S A ACE DGE ..≌△△， ∴EG = EC ．【总结】本题主要考查等腰直角三角形的性质以及线段垂直平分线的性质．【例8】 如图，已知：△ABC 中，AB = CB ，点D 在线段AC 上，且AB = AD ，∠ABC =108°，过点A 作AE ∥BC ，交∠ABD 的平分线于E ，联结CE ． 求证：BD 垂直平分EC ．【解析】连接ED∵AB = CB ，∠ABC =108°，∴︒=∠=∠36BCA BAC ∵AB = AD ，∴︒=∠=∠72ADB ABD ， ∴︒=︒-︒=∠3672108DBC∵BE 平分ABD ∠，∴︒=∠=∠36EBD ABE ∵AE ∥BC ，∴︒=︒-︒=∠72108180BAE ， ∴BEA BAE ∠=∠，∴BE BA =又∵AB = CB ，∴BC BE =证得：()S A S BCD BED ..≌△△，∴CD DE =∵BE BA =，CD DE =，∴ BD 垂直平分EC ．【总结】本题主要考查等腰三角形的性质以及线段垂直平分线的性质．二、 角平分线的性质定理和角平分线的性质定理的逆定理1、 角的平分线上的点到这个角两边的距离相等．2、 在一个角的内部（包括顶点）到这个角两边距离相等的点，在这个角的平分线上注意：角的平分线可以看作是在这个角的内部（包括顶点）到这个角两边距离相等的点的集合．【例9】 如图，//AD BC AC ，平分BAD ∠，BE 平分ABC ∠，交CD 于点E ，交AC 于点F ．求证：点F 到EA EC 、的距离相等． 【答案】见解析【解析】∵AC 平分BAD ∠，∴DAC BAC ∠=∠∵BC AD ∥，∴DAC ACB ∠=∠ ∴BAC ACB ∠=∠，∴BC AB =证得：()S A S CBE BAE ..≌△△，∴CEB AEB ∠=∠ ∴点F 到EA EC 、的距离相等．【总结】本题主要考查角平分线的意义和逆定理的运用．例题解析知识精讲模块二：角平分线AFBDEC6 / 15FG EBPON CDM A 【例10】 如图，90B C ∠=∠=°，M 是BC 的中点，DM 平分ADC ∠．求证：AM 平分DAB ∠． 【答案】见解析【解析】过M 作MN ⊥AD ，垂足为N∵DM 平分ADC ∠，∴CM MN =∵M 是BC 的中点，∴MB CM =，∴MB MN = ∴AM 平分DAB ∠．【总结】本题主要考查角平分线的性质定理和逆定理的运用．【例11】已知：如图，//AD OB OC ，平分AOB P ∠，是OC 上一点，过点P 作直线MN ，分别交AD OB 、于点M 和N ，且MP NP =． 求证：点P 到AO 和AD 的距离相等． 【答案】见解析【解析】过P 作PE ⊥OB 于点E ，PF ⊥OA 于点F ，PG ⊥AD 于点G ．∵OC 平分AOB ∠，∴PF PE =可证得：()S A A PGM PEN ..≌△△，则PG PE =，∴PG PF = ∴点P 到AO 和AD 的距离相等．【总结】本题主要考查角平分线的性质定理和逆定理的运用．【例12】如图，AD 为ABC ∆的角平分线，//DE AC ，交AB 于E ，过E 作AD 的垂线交BC 延长线于F ． 求证：B FAC ∠=∠．【解析】∵AD 为ABC ∆的角平分线，∴DAC BAD ∠=∠∵//DE AC ，∴DAC EDA ∠=∠ ∴EDA BAD ∠=∠，∴AE DE = ∵AD EF ⊥，∴EF 垂直平分AD ， ∴FD FA =，∴FDA FAD ∠=∠∵DAC FAC FAD ∠+∠=∠，BAD B FDA ∠+∠=∠ ∴B FAC ∠=∠．【总结】本题主要考查线段垂直平分性质定理及平行线+角平分线可以得到等腰三角形这个基本模型的运用．CMA DBABC DEF【例13】 已知：如图，在等腰直角三角形ABC 中，90ACB ∠=°，D 为BC 的中点，且DE AB ⊥，垂足为点E ，过点B 作//BF AC 交DE 的延长线于点F ，联结CF ．（1）求证：AD CF ⊥；（2）联结AF ，试判断ACF ∆的形状，并说明理由．【解析】（1）∵ABC △为等腰直角三角形，∴︒=∠=∠45CBA CAB ∵//BF AC ，∴︒=∠45ABF证得：FBE DBE ≌△△，则可得DB BF = ∵D 为BC 的中点，∴DB CD =，∴BF CD = 证得：()S A S BCF CAD ..≌△△，∴BCF CAD ∠=∠∵︒=∠+∠90ACF BCF ，∴︒=∠+∠90ACF CAD ，∴AD CF ⊥； （2）等腰三角形．由（1）可得：AF AD =，CF AD =，∴CF AF = ∴ACF △是等腰三角形．【总结】本题主要考查等腰直角三角形的性质，本题（1）中的全等是一个基本模型，要注意理解，在后期证明中也会经常用到．【例14】如图，AP BP 、分别平分MAB ∠和NBA ∠，PC PD 、分别垂直于AM BN 、，如果123AC cm CP cm BD cm ===，，，那么PD =_______，AB = _________．【答案】2cm ，4cm ．【解析】过P 作PE ⊥AB 于E ．∵AP BP 、分别平分MAB ∠和NBA ∠ ∴2===PD PE PC可证：()S A A PEA PCA ..≌△△，()S A A PDB PEB ..≌△△ 则CE AC =，BE BD = ∴431=+=+=EB AE AB【总结】本题主要考查角平分线的性质定理和逆定理的运用．【例15】如图，ABC ∆中，90C ∠=°，点O 为ABC ∆的三条角平分线的交点，OD BC ⊥，OE AC ⊥，OF AB ⊥，点D E F 、、分别为垂足，且1086AB BC CA ===，，，则点OPBCAM NDAEFABCDEF8 / 15GFEDCBA GFDA到三边AB AC 、和BC 的距离分别为_______． 【答案】2． 【解析】∵24862121=⨯⨯=⋅⋅=BC AC S ABC △ ∴ABC ABO OBC AOC S S S S =++△△△△111108624222OF OD OE =⨯⨯+⨯⨯+⨯⨯=∵点O 为ABC ∆的三条角平分线的交点， ∴OF OE OD == ∴2=OD【总结】本题一方面考查角平分线的性质定理，另一方面考查等积法的运用．【例16】如图，在ABC ∆中，90ACB ∠=°，AC BC =，AD 是BC 边上的中线，过C 作CF AD ⊥，E 为垂足，延长CE 交AB 于F ．求证：ADC BDF ∠=∠． 【答案】见解析【解析】过B 作BG ∥AC 交CF 的延长线于G ．证得：()A S A BCG CAD ..≌△△， ∴BG CD =，G ADC ∠=∠ ∵D 为BC 的中点， ∴DB CD =，∴BG BD =证得：()S A S GBF DBF ..≌△△，则可得G BDF ∠=∠ ∴ADC BDF ∠=∠【总结】本题一方面考查直角三角形的性质，另一方面考查全等的基本模型．【例17】如图，已知正方形ABCD 中，F 是CD 的中点，E 是BC 边上的一点，且AE DC CE =+．求证：AF 平分DAE ∠．EQ PDCBA 【答案】见解析【解析】连接EF 交AD 的延长线于G ．可证得：()A S A ECF GDF ..≌△△，则DG CE =，FG EF = ∵BC AD =，AE DC CE =+ ∴AE AG =可证得：()S S S AGF AEF ..≌△△， ∴GAF EAF ∠=∠ 即AF 平分DAE ∠．【总结】本题主要考查利用中线倍长构造全等，总而证明角平分线的成立．【例18】已知：如图，正方形ABCD 的边长为1，AB AD 、上各有一点P Q 、，若APQ∆的周长为2．求PCQ ∠的度数． 【答案】45°．【解析】∵APQ ∆的周长为2，∴2=++PQ AP AQ ．∵正方形ABCD 的边长为1，∴2=+++PB AP AD AQ ∴BP DQ PQ +=． 延长PB 至E ，使得BE =DQ可证：()S A S CBE CDQ ..≌△△，则CE CQ =，BCE DCQ ∠=∠ ∵BP DQ PQ +=，DQ BE =，∴EP PQ = 可证：()S S S CPE CPQ ..≌△△，∴PCE QCP ∠=∠ ∵︒=∠+∠90BCQ DCQ ，BCE DCQ ∠=∠， ∴︒=∠+∠90BCQ BCE ，即︒=∠90QCE 又∵︒=∠+∠90PCE QCP ，PCE QCP ∠=∠ ∴︒=∠45PCQ【总结】本题综合性较强，主要考查了全等的运用，以及截长补短辅助线的添加，最终目的是构造全等，在解题时要注意认真分析．【习题1】ABC ∆的边长AC BC 、的中垂线交AB 于一点O ，且OC BC =，则A∠随堂检测10 / 15EODCBA=________． 【答案】30°【解析】∵ABC ∆的边长AC BC 、的中垂线交AB 于一点O ，∴OC OB OA ==∴OCB B ∠=∠，ACO A ∠=∠ ∵︒=∠+∠+∠+∠180ACO A OCB B ∴︒=∠+∠90OCB ACO ，即︒=∠90ACB ∵OC BC =∴OBC △为等边三角形，∴︒=∠60B ∵︒=∠+∠90A B ，∴︒=∠30A ．【总结】本题主要考查线段垂直平分线性质以及等边三角形的性质．【习题2】 △ABC 中，AB = AC ，AC 的中垂线交AB 于E ，△EBC 的周长为20cm ，AB = 2BC ，则腰长为___________．【答案】cm 340．【解析】∵AC 的中垂线交AB 于E ，∴EC AE =∵△EBC 的周长为20cm ，∴20=+=++BC AB EC BC EB∵AB = 2BC ，∴340=AB【总结】本题主要考查线段垂直平分线性质以及等腰三角形的性质．【习题3】 如图所示，AB //CD ，O 为∠A 、∠C 的平分线的交点，OE ⊥AC 于E ，且OE =2， 则AB 与CD 之间的距离等于___________． 【答案】4【解析】过O 作OF ⊥AB 于F ，OG ⊥CD 于G∵O 为∠A 、∠C 的平分线的交点，∴2===OG OF OE ， ∵AB //CD ， ∴F 、O 、G 三点共线，∴4=FG ． 【总结】本题主要考查角平分线性质以及平行线的性质． 【习题4】ABC ∆中，AD 平分BAC ∠，DE DF 、分别垂直于AB AC 、，垂足分别为E F 、，如果48ABC S ∆=，79AC AB ==，，则DF =______________． 【答案】6【解析】∵AD 平分BAC ∠，∴DF DE =∵487219212121=⨯⨯+⨯⨯=⋅⋅+⋅⋅=+=DF DE DF AC DE AB S S S ADC ABD ABC △△△MNABC ∴6=DF【总结】本题主要考查角平分线性质以及等积法的运用．【习题5】 已知：点A 和点D 都是线段BC 外一点，且AB = AC ，DB = DC ，E 是AD 上一点．求证：BE = CE ．【答案】见解析【解析】∵AB = AC ，∴A 在线段BC 的垂直平分线上，∵DB = DC ，∴D 在BC 的垂直平分线上， ∴AD 是BC 的垂直平分线 ∵E 是AD 上一点 ∴BE = CE【总结】本题主要考查线段垂直平分线性质定理及其逆定理的运用．【习题6】 已知：如图，在ABC ∆中，90C ∠=°，30A ∠=°，MN 是AB 的垂直平分线．求证：12CM AM =．【答案】见解析． 【解析】∵MN 是AB 的垂直平分线，∴︒=∠=∠30MBA A∵90C ∠=°，30A ∠=°，∴︒=∠60CBA ，∴︒=︒-︒=∠303060CBM ， ∴NBM CBM ∠=∠，∴MN CM =． 在直角△AMN 中，︒=∠30A ，则AM MN 21=，∴AM CM 21=． 【总结】本题主要考查线段垂直平分线性质以及直角三角形的性质．【习题7】 已知：如图，ABC ∆中，90A ∠=°，AB AC BD ==，ED BC ⊥．求证：AE DE DC ==． 【答案】见解析 【解析】连接BE可证：()L H BDE BAE .≌△△，∴DE AE = ∵90A ∠=°，AB AC =， ∴︒=∠45C ∵ED BC ⊥∴△DEC 为等腰直角三角形， ∴DC DE =BEACD12 / 15ABCDOEF∴AE DE DC ==【总结】本题一方面考查了直角三角形全等的判定方法，另一方面考查了等腰直角三角形的性质，由于部分学生还未学过（H ．L ）的判定定理，因此可选择性的讲解．【习题8】 如图，在ABC ∆中，BD 平分ABC ∠，EF 垂直平分BD 交CA 延长线于E ．求证：EAB EBC ∠=∠． 【答案】见解析【解析】∵EF 垂直平分BD∴ED EB = ∴EDB EBD ∠=∠ ∵BD 平分ABC ∠， ∴ABD DBC ∠=∠∵ABD EDB EAB ∠+∠=∠，DBC EBD EBC +∠=∠ ∴EAB EBC ∠=∠【总结】本题一方面考查线段垂直平分线的性质定理，另一方面考查三角形外角性质的运用．【习题9】 已知：如图，在凹四边形ABCD 中，EO 垂直平分BC ，FO 垂直平分AD ，EO与FO 相交于点O ，且AB CD =． 求证：ABO DCO ∠=∠． 【答案】见解析 【解析】连接OD 、OA∵EO 垂直平分BC ∴OC OB = ∵FO 垂直平分AD ∴OD OA =可证：()S S S DOC AOB ..≌△△ ∴ABO DCO ∠=∠．【总结】本题主要考查线段垂直平分线以及角平分线性质定理的综合的运用．课后作业ABCDEF【作业1】 如图，Rt ABC ∆中，90C ∠=°，AD 平分BAC ∠，DE AB ⊥于E ，如果14DC cm AB cm ==，，那么ABD S ∆=___________．【答案】2【解析】∵AD 平分BAC ∠，DE AB ⊥，90C ∠=°， ∴1==DE CD∴2142121=⨯⨯=⋅⋅=DE AB S ABD △．【总结】本题主要考查角平分线性质定理的运用．【作业2】 如图，已知ABC ∆中，DE 是AC 的垂直平分线，5AC =，ABD ∆的周长为13，求ABC ∆的周长． 【答案】18【解析】∵DE 是AC 的垂直平分线，∴DC AD =∵ABD ∆的周长为13， ∴13=++AD BD AB ∴ABC ∆的周长为：AB AC BC AB AC BD DC AB AC BD AD ++=+++=+++13518=+=．【总结】本题主要考查线段垂直平分线性质定理的运用．【作业3】 如图，在ABC ∆中，已知点D 在BC 上，且DB AD BC +=．求证：点D 在AC的垂直平分线上． 【答案】见解析【解析】∵DB AD BC +=，BC DC DB =+∴DC AD =∴点D 在AC 的垂直平分线上．【总结】本题主要考查线段垂直平分线性质定理逆定理的运用，证明点在线段垂直平分线上． 【作业4】 如图，在ABC ∆中，AB AC =，120BAC ∠=°，AC 的垂直平分线DE 交BC 于D E ，为垂足，且18BC cm =，求DE 的长．【答案】3cm【解析】∵AB AC =，120BAC ∠=°，∴︒=∠=∠30C B∵AC 的垂直平分线DE 交BC 于D ∴DC AD =，︒=∠=∠30CAD C ，ABCEDAB C DD BACEADBEC14 / 15ED CBA ∴︒=︒-︒=∠9030120BAD在直角△BAD 中，︒=∠30B ，则BD AD 21= ∴182=+=+=DC DC DC BD BC ∴6=DC在直角△CED 中，︒=∠30C ，则321==DC DE ．【总结】本题主要考查线段垂直平分线性质定理及其直角三角形性质的运用．【作业5】 如图，正方形ABCD 的边长为1，AE 是CAB ∠的平分线，交BC 于点E ，则点E 到AC 的距离为___________． 【答案】12-．【解析】过E 作EF ⊥AC ，垂足为F可得：△CEF 为等腰直角三角形， 则由勾股定理可得：EF CE 2=∵AE 是CAB ∠的平分线，EF ⊥AC ，90B ∠= ∴BE EF = 又∵1=+EB CE ∴12=+EF EF ∴12-=EF【总结】本题综合性较强，主要考查了角平分线的性质以及正方形的性质，还运用勾股定理计算线段长．【作业6】 如图，已知ABC ∆中，点E 是AB 延长线上的一点，AE AC AD =，平分BAC ∠，BD = BE ．求证：2ABC C ∠=∠． 【答案】见解析【解析】由题意，易得：()S A S ACD AED ..≌△△则：C E ∠=∠∵BD = BE ，∴BDE E ∠=∠ ∴C E DBE E ABC ∠=∠=∠+∠=∠22ABCDE【总结】本题主要考查等边对等角以及三角形外角性质的运用，解题时注意分析，当看到证明一个角是另一个角的两倍时，通常都考虑采用外角性质证明．【作业7】 如图，在ABC ∆中，AD BC ⊥于D ，AC CD BD +=．求证：2C B ∠=∠． 【答案】见解析【解析】在BD 上截取一点E ，使得DE =DC∵DC DE =，AC CD BD += ∴AC BE =可证：AED ACD ≌△△，则AE AC =，AED C ∠=∠ ∴AE BE =，∴BAE B ∠=∠ ∴C B BAE B AED ∠=∠=∠+∠=∠22 ∴2C B ∠=∠【总结】本题一方面考查了截长补短辅助线的添加，主要是看到两条线段和等于第三条线段的模型，另一方面考查了证明一个角是另一个角的两倍的基本模型，通常都考虑采用外角性质证明．ABCD。

第九讲 全等三角形培优———线段的垂直平分线与角平分线一、线段垂直平分线 1、线段垂直平分线的性质（1）线段的对称轴是（2）垂直平分线性质定理：定理的几何符号表示：如图 12、线段垂直平分线判定定理：定理的几何符号表示：如图1，定理的作用：证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的性质（1）三角形三边的垂直平分线 ，并且这一点到 的距离相等. （2）三角形三边垂直平分线的交点位置与三角形形状的关系：若三角形是锐角三角形，则它三边垂直平分线的交点在三角形 ；若三角形是直角三角形，则它三边垂直平分线的交点是 ； 若三角形是钝角三角形，则它三边垂直平分线的交点在三角形 .经典例题：例1 如图1，在△ABC 中，BC ＝8cm ，AB 的垂直平分线交AB 于点D ，交边AC 于点E ，△BCE 的周长等于18cm ，则AC 的长等于（ ） A ．6cm B ．8cm C ．10cm D ．12cm 针对性练习：已知：1)如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点E ，如果△EBC 的周长是24cm ，那么BC=2) 如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点E ，如果BC=8cm ， 那么△EBC 的周长是 3）如图，AB=AC,AB 的垂直平分线交AB 于点D ，交AC 于点E ，如 果∠A=28度，那么∠EBC 是4. 如图，在直角△ABC 中，∠C=90°，∠CAB 的平分线AD 交BC 于D ，若DE 垂直平分AB ，求∠B 的度数．图1C例2. 已知：在△ABC 中，ON 是AB 的垂直平分线,OA=OC求证：点O 在BC 的垂直平分线针对性练习：已知如图，在△ABC 中，AB =AC ，O 是△ABC 内一点，且OB =OC ， 求证：AO 垂直平分B C.例3. 在△ABC 中，AB=AC ，AB 的垂直平分线与边AC 所在的直线相交所成锐角为50°，△ABC 的顶角∠B 的大小为_______________。

【拔尖特训】2024-2025学年八年级数学上册尖子生培优必刷题（人教版）专题13.2线段的垂直平分线专题（限时满分培优训练）班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷满分100分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2022秋•防城港期末）如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，连接AE，若AE＝4，EC＝2，则BC的长是（）A．8B．6C．4D．22．（2022秋•东宝区期末）和三角形三个顶点的距离相等的点是（）A．三条角平分线的交点B．三边中线的交点C．三边上高所在直线的交点D．三边的垂直平分线的交点3．（2022秋•黄石港区期末）如图，在△ABC中，AC＝4cm，线段AB的垂直平分线交AB，AC于点M，N，△BCN的周长是7cm，则BC的长为（）A．4cm B．3 cm C．2cm D．1cm4．（2022秋•长安区校级期末）某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该在△ABC（）A．三条高线的交点处B．三条中线的交点处C．三个角的平分线的交点处D．三条边的垂直平分线的交点处5．（易错题）（2023秋•青秀区校级月考）已知：△ABC是三边都不相等的三角形，点P是三个内角平分线的交点，点O是三边垂直平分线的交点，当P、O同时在不等边△ABC的内部时，那么∠BOC和∠BPC 的数量关系是（）A．2∠BOC+∠BPC＝360°B．∠BOC+2∠BPC＝360°C．3∠BOC﹣∠BPC＝360°D．4∠BPC﹣∠BOC＝360°6．（易错题）（2022秋•汉南区校级期末）如图，锐角三角形ABC中，O为三条边的垂直平分线的交点，I 为三个角的平分线的交点，若∠BOC的度数为x，∠BIC的度数为y，则x、y之间的数量关系是（）A．x+y＝90°B．x﹣2y＝90°C．x+180°＝2y D．4y﹣x＝360°7．（易错题）（2022秋•东阿县校级期末）如图，线段AB，BC的垂直平分线l1、l2相交于点O．若∠OEB ＝46°，则∠AOC＝（）A．92°B．88°C．46°D．86°8．（易错题）（2022春•雅安期末）如图所示，在△ABC中，DM，EN分别垂直平分AB和AC，交BC于点D，E，若∠DAE＝40°，则∠BAC＝（）A．105°B．100°C．110°D．140°9．（培优题）（2022春•舞钢市期末）如图，四边形ABCD中，DE和DF恰好分别垂直平分AB和BC，则以下结论不正确的是（）A．AD＝CD B．∠B＝∠A+∠CC．∠EDF＝∠ADE+∠CDF D．BE＝BF10．（培优题）（2022春•周村区期末）如图，在△ABC中，∠BAC＝80°，边AB的垂直平分线交AB于点D，交BC于点E，边AC的垂直平分线交AC于点F，交BC于点G，连接AE，AG．则∠EAG的度数为（）A．35°B．30°C．25°D．20°二．填空题（共6小题）11．（2022秋•句容市期末）如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，连接AE，若AE＝4，EC＝2，则BC的长．12．（2022秋•德城区校级期末）如图，在△ABC中，AF平分∠BAC，AC的垂直平分线DE交BC于点E，交AC于点D，∠B＝70°，∠F AE＝19°，则∠C＝°．13．（易错题）（2023春•甘州区校级期末）如图，在△ABC中，AC的垂直平分线与AC，BC分别交于点E，D，CE＝4，△ABC的周长是25，则△ABD的周长为．14．（易错题）（2023春•荔湾区期末）在平面直角坐标系中，已知A（8，0），B（0，4），作AB的垂直平分线交x轴于点C，则点C坐标为．15．（2023春•振兴区校级期中）如图，AE是∠CAM的角平分线，点B在射线AM上，DE是线段BC的中垂线交AE于E，过点E作AM的垂线交AM于点F．若∠ACB＝26°，∠EBD＝25°，则∠AED＝．16．（2023春•振兴区校级期中）如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，这两条垂直平分线分别交BC于点D、E．已知△ADE的周长为11cm，分别连接OA、OB、OC，若△OBC的周长为23cm，则OA的长为．三．解答题（共7小题）17．（2023•渭南一模）如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，求证：AD 垂直平分EF．18．（2022春•合浦县期中）如图，已知点D是BC上一点，DE⊥AB，DF⊥AC，垂足分别为E、F，连接AD，若AD垂直平分EF，求证：AD是△ABC的角平分线．19．（易错题）（2023春•新民市期中）如图，在△ABC中，∠C＝90°，点P在AC上运动，点D在AB上，PD始终保持与P A相等，BD的垂直平分线交BC于点E，交BD于点F，连接DE．（1）判断DE与DP的位置关系，并说明理由；（2）若AC＝6，BC＝8，P A＝2，求线段DE的长．20．（易错题）（2023春•丰城市期末）如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G．（1）若BC＝9，求△AEG的周长．（2）若∠BAC＝130°，求∠EAG的度数．21．（培优题）（2023春•榆林期末）如图，在△ABC中，AC边的垂直平分线分别交BC、AC于点E、F，连接AE，作AD⊥BC于点D，且D为BE的中点．（1）试说明：AB＝CE；（2）若∠C＝32°，求∠BAC的度数．22．（培优题）（2023春•定边县校级期末）已知，如图，AD是△ABC的高线，AD的垂直平分线分别交AB，AC于点E，F．（1）若∠B＝40°，求∠AEF的度数；（2）求证：∠B=12∠AED．23．（培优题）（2023春•兴庆区校级期末）如图，△ABC中，D、E在AB上，且D、E分别是AC、BC的垂直平分线上一点．（1）若△CDE的周长为4，求AB的长；（2）若∠ACB＝100°，求∠DCE的度数；（3）若∠ACB＝a（90°＜a＜180°），则∠DCE＝．。

线段的垂直平分线、角平分线经典习题及答案由于A、B都在CD的垂直平分线上，所以直线AB是CD的垂直平分线。

证毕。

例4：解：连接EF，由于AB=AC，所以∠BAC=60°，∴∠DEG=30°，∠GFC=60°，又因为DE⊥AB，FG⊥AC，所以DEGF是一个菱形，且DG=GF=7.5cm，所以EG=2DGsin30°=7.5cm。

例5：证明：因为BD=BC，所以∠XXX∠CBD，又因为BE⊥CD，CF⊥BD，所以∠BEC=∠BCF，所以BE平分∠XXX，CF平分∠CBD，又因为∠XXX∠CBD，所以BE和CF都平分∠BCD，即BE垂直平分CD。

证毕。

例6：证明：连接OF，OE，MN，∵MN∥BC，∴∠EOF=∠ACB，又∠XXX∠EOM+∠MOF，∠XXX∠EOM+∠EOF，∴∠MOF=∠ACB-∠EOF，又因为EF是AC的角平分线，∴∠XXX∠EAF，又因为EF是AC的外角平分线，∴∠XXX∠XXX，∴∠MOF=∠ACB-∠XXX，又因为OE⊥AC，OF⊥AC，所以OE=OF，证毕。

例7：证明：连接AD，因为AD是∠A的平分线，所以∠EAD=∠FAD，又因为BD=BC，所以∠XXX∠DCB，又因为AD⊥DE，所以∠EDB=90°-∠XXX，又因为DF⊥CF，所以∠XXX°-∠DCB，所以∠EDB=∠XXX，又因为∠EAD=∠FAD，所以三角形ADE与三角形ADF全等，所以DE=DF，又因为BE⊥DE，CF⊥DF，所以BE=DEsin∠EDB=DFsin∠FDC=CF，证毕。

例4：根据题意，作AH垂直BC于点H，可以得到HC 的长度为15/2.由于△ABC是等腰三角形，所以∠ACB=∠ABC=30°。

根据正弦定理，可以求得AC的长度为5√3.由于F是AC的中点，所以FC的长度为5/2√3.根据勾股定理，可以得到CG和BE的长度都为5.因此，EG的长度也为5.例5：由于DE垂直于AB，而∠ACB=90°，所以∠BDE=∠ACB=90°。

垂直平分线角平分线培优提高练习一．选择题（共6小题）1．如果三角形内有一点到三边距离相等，且到三顶点的距离也相等，那么这个三角形的形状是（）A．等腰三角形B．直角三角形C．等腰直角三角形D．等边三角形2．下列各语句中不正确的是（）A．全等三角形的周长相等B．全等三角形的对应角相等C．到角的两边距离相等的点在这个角的平分线上D．线段的垂直平分线上的点到这条线段的两端点的距离相等3．如图，直线CP是AB的中垂线且交AB于P，其中AP=2CP．甲、乙两人想在AB上取两点D、E，使得AD=DC=CE=EB，其作法如下：（甲）作∠ACP、∠BCP之角平分线，分别交AB于D、E，则D、E即为所求；（乙）作AC、BC之中垂线，分别交AB于D、E，则D、E即为所求．对于甲、乙两人的作法，下列判断何者正确（）A．两人都正确B．两人都错误C．甲正确，乙错误D．甲错误，乙正确4．如图，在四边形ABCD中，M、N分别是CD、BC的中点，且AM⊥CD，AN⊥BC，已知∠MAN=74°，∠DBC=41°，则∠ADC度数为（）A．45°B．47°C．49°D．51°5．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为（）A．B．C．D．66．如图，四边形ABCD中，∠C=50°，∠B=∠D=90°，E、F分别是BC、DC上的点，当△AEF 的周长最小时，∠EAF的度数为（）A．50°B．60°C．70°D．80°二．填空题（共5小题）7．△ABC中，DF是AB的垂直平分线，交BC于D，EG是AC的垂直平分线，交BC于E，若∠DAE=30°，则∠BAC等于．8．如图，△ABC中，D是AB的中点，DE⊥AB，∠ACE+∠BCE=180°，EF⊥AC交AC于F，AC=12，BC=8，则AF=．9．在△ABC中，AB、AC的垂直平分线分别交BC于点D、E．若BC=10，DE=4，则AD+AE=．10．△ABC中，∠C=90°，DE是AB的中垂线，AB=2AC，且BC=18cm，则BE的长度是．11．如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，△PMN的周长为．三．解答题（共6小题）12．如图，△ABC中，∠A=60°，∠ACB的平分线CD和∠ABC的平分线BE交于点G．求证：GE=GD．13．已知如图，CD是RT△ABC斜边上的高，∠A的平分线交CD于H，交∠BCD的平分线于G，求证：HF∥BC．14．在△ABC中，AB边的垂直平分线交直线BC于点D，垂足为点F，AC边的垂直平分线交直线BC于点E，垂足为点G．（1）当∠BAC=100°（如图）时，∠DAE=°；（2）当∠BAC为一任意角时，猜想∠DAE与∠BAC的关系，并证明你的猜想．15．△ABC为等腰直角三角形，∠ABC=90°，点D在AB边上（不与点A、B重合），以CD为腰作等腰直角△CDE，∠DCE=90°．（1）如图1，作EF⊥BC于F，求证：△DBC≌△CFE；（2）在图1中，连接AE交BC于M，求的值；（3）如图2，过点E作EH⊥CE交CB的延长线于点H，过点D作DG⊥DC，交AC于点G，连接GH．当点D在边AB上运动时，式子的值会发生变化吗？若不变，求出该值；若变化请说明理由．。

专题2.6角平分线的性质姓名：__________________ 班级：______________ 得分：_________________注意事项：本试卷满分100分，试题共24题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2020•碑林区校级模拟）如图，在Rt △ABC 中，∠C ＝90°，AD 是∠BAC 的平分线，若AC ＝3，BC ＝4，则S △ABD ：S △ACD 为（ ）A ．5：4B ．5：3C ．4：3D ．3：4【分析】过D 作DF ⊥AB 于F ，根据角平分线的性质得出DF ＝DC ，再根据三角形的面积公式求出△ABD 和△ACD 的面积，最后求出答案即可．【解析】过D 作DF ⊥AB 于F ，∵AD 平分∠CAB ，∠C ＝90°（即AC ⊥BC ），∴DF ＝CD ，设DF ＝CD ＝R ， 在Rt △ABC 中，∠C ＝90°，AC ＝3，BC ＝4，由勾股定理得：AB =√32+42=5，∴S △ABD =12×AB ×DF =12×5×R =52R ，S △ACD =12×AC ×CD =12×3×R =32R ，∴S △ABD ：S △ACD ＝（52R ）：（32R ）＝5：3， 故选：B ．2．（2020春•高明区期末）如图，在Rt △ABC 中∠C ＝90°，BD 是∠ABC 的平分线，若CD ＝4，AB ＝14，则S △ABD ＝（ ）A ．56B ．28C ．14D ．12【分析】过点D 作DE ⊥AB 于E ，根据角平分线上的点到角的两边距离相等可得DE ＝CD ，再利用三角形的面积公式列式计算即可得解．【解析】如图，过点D 作DE ⊥AB 于E ，∵BD 是∠ABC 的平分线，∠C ＝90°，∴DE ＝CD ＝4，∴△ABD 的面积=12AB •DE =12×14×4＝28．故选：B ．3．（2020•怀化）在Rt △ABC 中，∠B ＝90°，AD 平分∠BAC ，交BC 于点D ，DE ⊥AC ，垂足为点E ，若BD ＝3，则DE 的长为（ ）A ．3B ．32C ．2D ．6【分析】根据角平分线的性质即可求得．【解析】∵∠B ＝90°，∴DB ⊥AB ，又∵AD 平分∠BAC ，DE ⊥AC ，∴DE ＝BD ＝3，故选：A．4．（2020春•龙岗区期末）如图，点P是∠AOB的角平分线上一点，过点P作PC⊥OA于点C，且PC＝3，则点P到OB的距离为（）A．3B．4C．5D．6【分析】过点P作PD⊥OB于D，根据角平分线上的点到角的两边距离相等可得PC＝PD，从而得解．【解析】如图，过点P作PD⊥OB于D，∵点P是∠AOB的角平分线上一点，PC⊥OA，∴PC＝PD＝3，即点P到OB的距离等于3．故选：A．5．（2020春•锦江区期末）点P在∠AOB的角平分线上，点P到OA边的距离等于10，点Q是OB边上的任意一点，下列选项正确的是（）A．PQ＜10B．PQ＞10C．PQ≥10D．PQ≤10【分析】过P作PD⊥OB于D，根据角平分线的性质得出PC＝PD＝10，再根据垂线段最短得出即可．【解析】过P 作PD ⊥OB 于D ，∵PC ⊥OA ，PD ⊥OB ，OP 平分∠AOB ，∴PC ＝PD ，∵点P 到OA 边的距离等于10，∴PD ＝PC ＝10，∴PQ ≥10（当Q 与点D 重合时，PQ ＝10），故选：C ． 6．（2020•岐山县二模）如图，在Rt △ABC 中，∠C ＝90°，∠BAC 的平分线交BC 于点D ，CD ＝2，Q 为AB 上一动点，则DQ 的最小值为（ ）A ．2B ．2√2C ．√3D ．52 【分析】作DH ⊥AB 于H ，如图，根据角平分线的性质得到DH ＝DC ＝2，然后根据垂线段最短求解．【解析】作DH ⊥AB 于H ，如图，∵AD 平分∠BAC ，DH ⊥AB ，DC ⊥AC ，∴DH ＝DC ＝2，∵Q 为AB 上一动点，∴DQ 的最小值为DH 的长，即DQ 的最小值为2．故选：A ．7．（2020•丽水模拟）在Rt △ABC 中，∠C ＝90°，小明进行如图步骤尺规作图，根据操作，对结论判断正确的序号是（）①AD平分∠BAC；②AC＝2DG；③S△ADC＝S△ABD；④S△ADC＝2S△ADG．A．①②③④B．③④C．②③D．②③④【分析】利用基本作图得到DG⊥BC，BD＝CD，则AD为△ABC的中线，则可对①进行判断；再证明DG为△ABC的中位线，则可对②进行判断；然后根据三角形面积公式对③④进行判断．【解析】由作法得DG垂直平分BC，∴DG⊥BC，BD＝CD，∴AD为△ABC的中线，所以①错误；∵∠C＝90°，∴DG∥AC，∴DG为△ABC的中位线，∴AC＝2DG，所以②正确；BG＝AG，∴S△ADC＝S△ABD，所以③正确；S△ADG＝S△BDG，∴S△ADC＝2S△ADG，所以④正确．故选：D．8．（2020•南山区模拟）如图，△ABC中，AB＝5，AC＝4，以点A为圆心，任意长为半径作弧，分别交AB、AC于D和E，再分别以点D、E为圆心，大于二分之一DE为半径作弧，两弧交于点F，连接AF并延长交BC于点G，GH⊥AC于H，GH＝2，则△ABG的面积为（）A．4B．5C．9D．10【分析】作GM⊥AB于M，如图，先利用基本作图得到AG平分∠BAC，再根据角平分线的性质得到GM ＝GH＝2，然后根据三角形面积公式计算．【解析】作GM⊥AB于M，如图，由作法得AG平分∠BAC，而GH⊥AC，GM⊥AB，∴GM＝GH＝2，∴S△ABG=12×5×2＝5．故选：B．9．（2020•长春模拟）如图，∠MON＝60°．①以点O为圆心，2cm长为半径画弧，分别交OM、ON于点A、C；②在分别以A、C为圆心，2cm长为半径画弧，两弧交于点B；③连结AB、BC，则四边形OABC的面积为（）A．4√3cm2B．2√3cm2C．4cm2D．2cm2【分析】先确定OB是∠MON的角平分线，得出∠BON＝30°，作BD⊥ON于D，根据等腰三角形的性质得出∠BCN＝60°，解直角三角形求得BD，然后根据三角形面积公式求得△BOC的面积，进而求得四边形OABC的面积．【解析】由题意可知OB是∠MON的角平分线，∵∠MON＝60°，∴∠BON＝30°，作BD⊥ON于D，∵OC＝BC＝2，∴∠BOC＝∠OBC＝30°，∴∠BCN＝60°，∴BD=√32BC=√3，∴S△BOC=12×OC×BD=12×2×√3=√3，∴四边形OABC的面积＝2S△BOC＝2√3，故选：B．10．（2019秋•霸州市期末）如图，已知△ABC的周长是10，点O为∠ABC与∠ACB的平分线的交点，且OD⊥BC于D．若OD＝2，则△ABC的面积是（）A．20B．12C．10D．8【分析】作OE⊥AB于E，OF⊥AC于F，连接OA，根据角平分线的性质得到OE＝OF＝OD＝2，根据三角形的面积公式计算即可．【解析】作OE⊥AB于E，OF⊥AC于F，连接OA，∵O为∠ABC与∠ACB的平分线的交点，OD⊥BC，OE⊥AB，OF⊥AC，∴OE＝OF＝OD＝2，∴△ABC的面积＝△AOB的面积+△BOC的面积+△AOC的面积=12×（AB+BC+AC）×OD=12×10×2＝10，故选：C．二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2020春•宁德期末）如图，已知△ABC，∠C＝90°，BD是△ABC的角平分线，若AD＝3，CD＝2，则点D到AB边的距离为2．【分析】过点D作DE⊥AB于E，先求出CD，再根据角平分线上的点到角的两边的距离相等可得DE＝CD，即可得解．【解析】如图，过点D作DE⊥AB于E，∵∠C＝90°，BD是三角形的角平分线，∴DE＝CD＝2，即点D到AB边的距离是2．故答案为：2．12．（2020•湘潭）如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD＝3，点M是射线OC上一动点，则PM的最小值为3．【分析】根据垂线段最短可知当PM⊥OC时，PM最小，再根据角的平分线的性质，即可得出答案．【解析】根据垂线段最短可知：当PM⊥OC时，PM最小，当PM⊥OC时，又∵OP平分∠AOC，PD⊥OA，PD＝3，∴PM＝PD＝3，故答案为：3．13．（2020春•市北区期末）如图，△ABC中，AB＝2.5cm，AC＝6cm，BC＝6.5cm，∠ABC与∠ACB的角平分线相交于点P，过点P作PD⊥BC，垂足为点D，则线段PD的长为1cm．【分析】根据角平分线的性质得出PE＝PD＝PF，进而利用三角形的面积公式解答即可．【解析】过P点作PE⊥AB于E，PF⊥AC于F，∵∠ABC与∠ACB的角平分线相交于点P，过点P作PD⊥BC，PE⊥AB于E，PF⊥AC于F，∴PD＝PE，PD＝PF，∴PE＝PD＝PF，∵△ABC中，AB＝2.5cm，AC＝6cm，BC＝6.5cm，∴AB2+AC2＝BC2，∴△ABC是直角三角形，∴S△ABC=12×AB×AC=12AB⋅PE+12BC⋅PD+12AC⋅PF，即12×6×2.5=12PD ⋅(AB +AC +BC)=12PD ×(2.5+6+6.5)， 解得：PD ＝1（cm ），故答案为：1．14．（2020春•太原期末）如图，在△ABC 中，∠ACB ＝90°，AD 平分∠BAC 交BC 于点D ，CD ＝3，DB ＝5，点E 在边AB 上运动，连接DE ，则线段DE 长度的最小值为 3 ．【分析】当DE ⊥AB 时，线段DE 的长度最小，根据角平分线的性质得出CD ＝DE ，代入求出即可．【解析】当DE ⊥AB 时，线段DE 的长度最小（根据垂线段最短），∵AD 平分∠CAB ，∠C ＝90°，DE ⊥AB ，∴DE ＝CD ，∵CD ＝3，∴DE ＝3，即线段DE 的长度的最小值是3，故答案为：3．15．（2020春•南岗区校级期中）如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 于点F ，若△ABC 的面积为21cm 2，AB ＝8cm ，AC ＝6cm ，则DE 的长为 3 cm ．【分析】先根据角平分线的性质得到DE ＝DF ，再利用三角形面积公式得到12×AB ×DE +12×DF ×AC ＝21，所以12×8×DE +12×DE ×6＝21，然后解关于DE 的方程即可． 【解析】∵AD 为∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF ，∵S △ABD +S △ACD ＝S △ABC ，∴12×AB ×DE +12×DF ×AC ＝21， 即12×8×DE +12×DE ×6＝21，∴DE ＝3（cm ）．故答案为3．16．（2019秋•安居区期末）三条公路将A 、B 、C 三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是 ∠A 、∠B 、∠C 的角平分线的交点处 ．【分析】根据角平分线上的点到角的两边的距离相等解答即可．【解析】在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，根据角平分线的性质，集贸市场应建在∠A 、∠B 、∠C 的角平分线的交点处．故答案为：∠A 、∠B 、∠C 的角平分线的交点处．17．（2019秋•余姚市期末）在正方形网格中，∠AOB 的位置如图所示，点P ，Q ，M ，N 是四个格点，则这四个格点中到∠AOB 两边距离相等的点是 M 点．【分析】根据角的平分线上的点到角的两边的距离相等解答．【解析】由图形可知，点M 在∠AOB 的角平分线上，∴点M 到∠AOB 两边距离相等，故答案为：M ．18．（2019秋•南江县期末）如图，△ABC 的三边AB ，BC ，CA 的长分别为30，40，15，点P 是△ABC 三个内角平分线的交点，则S △P AB ：S △PBC ：S △PCA ＝ 6：8：3 ．【分析】先根据角平分线的性质得到P点到三边的距离相等，设这个距离为m，然后根据三角形面积公式得到S△P AB：S△PBC：S△PCA＝AB：BC：AC．【解析】∵点P是△ABC三个内角平分线的交点，∴P点到三边的距离相等，设这个距离为m，∴S△P AB：S△PBC：S△PCA=12×AB×m−12×BC×m−12×AC×m＝AB：BC：AC＝30：40：15＝6：8：3．故答案为6：8：3．三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）19．（2020春•南岗区期末）已知：在△ABC中，∠ABC＝60°，∠ACB＝40°，BD平分∠ABC，CD平分∠ACB，（1）如图1，求∠BDC的度数；（2）如图2，连接AD，作DE⊥AB，DE＝2，AC＝4，求△ADC的面积．【分析】（1）先根据角平分线的定义得到∠DBC＝30°，∠DCB＝20°，然后根据三角形内角和计算∠BDC的度数；（2）作DF⊥AC于F，DH⊥BC于H，如图2，根据角平分线的性质得到DH＝DE＝DH＝2，然后根据三角形面积公式计算△ADC的面积．【解析】（1）∵BD平分∠ABC，∴∠DBC=12∠ABC=12×60°＝30°，∵CD平分∠ACB，∴∠DCB=12∠ACB=12×40°＝20°，∴∠BDC＝180°﹣∠DBC﹣∠DCB＝180°﹣30°﹣20°＝130°；（2）作DF⊥AC于F，DH⊥BC于H，如图2，∵BD平分∠ABC，DE⊥AB，DH⊥BC，∴DH＝DE＝2，∵CD平分∠ACB，DF⊥AC，DH⊥BC，∴DF＝DH＝2，∴△ADC的面积=12DF•AC=12×2×4＝4．20．（2019秋•临西县期末）已知：如图，BP、CP分别是△ABC的外角平分线，PM⊥AB于点M，PN⊥AC 于点N．求证：P A平分∠MAN．【分析】作PD⊥BC于点D，根据角平分线的性质得到PM＝PD，PN＝PD，得到PM＝PN，根据角平分线的判定定理证明即可．【解析】证明：作PD⊥BC于点D，∵BP是△ABC的外角平分线，PM⊥AB，PD⊥BC，∴PM＝PD，同理，PN＝PD，∴PM＝PN，又PM⊥AB，PN⊥AC，∴P A平分∠MAN．21．（2019秋•呼和浩特期末）已知：如图，AD∥BC，DB平分∠ADC，CE平分∠BCD，交AB于点E，BD 于点O．求证：点O到EB与ED的距离相等．【分析】根据平行线的性质和角平分线的定义得到∠DOC＝90°，根据等腰三角形的三线合一证明即可．【解析】证明：∵AD∥BC，∴∠ADC+∠BCD＝180°，∵DB平分∠ADC，CE平分∠BCD，∴∠ODC+∠OCD＝90°，∴∠DOC＝90°，又CE平分∠BCD，∴CB＝CD，∴OB＝OD，∴CE是BD的垂直平分线，∴EB＝ED，又∠DOC＝90°，∴EC平分∠BED，∴点O到EB与ED的距离相等．22．（2019秋•涡阳县期末）已知：如图，△ABC的角平分线BE、CF相交于点P．求证：点P在∠A的平分线上．【分析】过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N，根据角平分线上的点到角的两边距离相等可得PD＝PM，同理可得PM＝PN，从而得到PD＝PN，再根据到角的两边距离相等的点在角的平分线上证明即可．【解析】证明：如图，过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N，∵BE平分∠ABC，点P在BE上，∴PD＝PM，同理，PM＝PN，∴PD＝PN，∴点P在∠A的平分线上．23．（2019秋•交城县期末）已知：如图，在Rt△ABC中，∠ACB＝90°，∠B＝60°，AD，CE是角平分线，AD与CE相交于点F，FM⊥AB，FN⊥BC，垂足分别为M，N．求证：FE＝FD．【分析】根据条件可得到FM＝FN，再根据角的度数可求得∠NEF＝75°＝∠MDF，可证明△EFM≌△DFN，可得到FE＝FD．【解析】证明：连接BF，∵F是△ABC的角平分线交点，∴BF也是角平分线，∵FM ⊥AB ，FN ⊥BC ，∴MF ＝FN ，∠DNF ＝∠EMF ＝90°，∵在Rt △ABC 中，∠ACB ＝90°，∠ABC ＝60°，∴∠BAC ＝30°，∴∠DAC =12∠BAC ＝15°，∴∠CDA ＝75°，∵∠NFC ＝45°，∠MFN ＝120°，∴∠MFE ＝15°，∴∠MEF ＝75°＝∠NDF ，在△DNF 和△EMF 中，{∠DNF =∠EMF ∠NDF =∠MEF NF =MF，∴△DNF ≌△EMF （AAS ），∴FE ＝FD ．24．（2019秋•潮州期末）如图，DE ⊥AB 于E ，DF ⊥AC 于F ，若BD ＝CD ，BE ＝CF求证：AD 平分∠BAC ．【分析】由DE ⊥AB 于E ，DF ⊥AC 于F ，若BD ＝CD ，BE ＝CF ，即可判定Rt △BDE ≌Rt △CDF （HL ），则可得DE ＝DF ，然后由角平分线的判定定理，即可证得AD 平分∠BAC ．【解析】证明：∵DE ⊥AB ，DF ⊥AC ，∴∠E ＝∠DFC ＝90°，在Rt △BDE 和Rt △CDF 中，{BD=CDBE=CF，∴Rt△BDE≌Rt△CDF（HL），∴DE＝DF，∴AD平分∠BAC．。

线段的垂直平分线练习（培优）一、选择题1.到三角形三个顶点距离相等的是( )A.三条中线交点B.三条高的交点C.三条角平分线的交点D.三条中垂线的交点2.线段AB外有两点C，D(在AB同侧)使CA=CB，DA=DB，∠ADB=80°, ∠CAD=10°,则∠ACB=( )A.90°B.100°C.110°D.120°3.BD为CE的中垂线，A在CB延长线上，∠C=34°,则∠ABE=( )A.17°B.34°C.68°D.136°4.O为△ABC三边中垂线的交点，则O称为△ABC的( )A.外心B.内心C.垂心D.重心5. 如图,△ABC中，∠ACB=90°, ∠A=30°AC的中垂线交AC于E.交AB于D，则图中60°的角共有( )A．6个 B.5个 C.4个D3个三、填空1.△ABC中，AB=AC，P为形内一点，PB=PC，则P在的中垂线上，P还在∠的平分线上.2.△ABC中，AB=AC=14，腰AB的中垂线交AC于D，△BCD周长为4cm,则BC= .3.正△ABC内一点O到三边距离相等，且OA=OB=OC.则∠BOC= .4.△ABC的边AC、BC的中垂线交于AB上一点O，且OC=BC，则∠A= .5.若PA=PB，DA=DB，则PD是AB的.四、解答1.△ABC中，∠C=90°,AB的中垂线交AB于D，AC于E.且∠EBC=40°,求∠A及∠BED的度数.2．如下图，在△ABC中，∠C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AB ＝20cm，求△ABC两锐角及AD、DE、EB各为多少？CH M D B A 3．如图，AD 、BE 分别是等边△ABC 中BC 、AC 上的高，M 、N 分别在AD 、BE 的延长线上，∠CBM ＝∠ACN ．求证：AM ＝BN ．NM E D CBA4．已知，△ABC 中，∠ABC 为锐角，且∠ABC ＝2∠ACB ，AD 为BC 边上的高，延长AB 到E ，使BE ＝BD ，连结ED 并延长交AC 于F ．求证：AF ＝CF ＝DF ．5.如图，AB⊥BC，CD⊥BC，∠AMB=︒75，∠DMC=︒45，AM=MD ．求证：AB=BC ．F ED C B参考答案【同步达纲练习】一、×××√×√二、D B C A B三、1.BC,BAC 2.10 3. .120° 4.30° 5.中垂线四、1. ∠C=180°, ∠EBC=40°∴∠BEC=50°又AE=BE∴∠A=25°∠DEB=65°。

专题06线段的垂直平分线与角平分线综合压轴题五种模型全攻略【考点导航】目录【典型例题】 (1)【考点一利用线段垂直平分线的性质求解】 (1)【考点二线段垂直平分线的判定】 (4)【考点三利用角平分线的性质求解】 (8)【考点四角平分线的判定】 (11)【考点五线段的垂直平分线与角平分线的综合问题】 (14)【过关检测】 (20)【典型例题】【考点一利用线段垂直平分线的性质求解】∴()SAS ADE CDE △△≌，∴36DCE A ==︒∠∠，∴72BEC A ACE ∠=∠+∠=︒，故答案为：72︒．【点睛】本题主要考查了三角形外角的性质，全等三角形的性质与判断，线段垂直平分线的定义，正确推出36DCE A ==︒∠∠是解题的关键．【变式训练】【答案】8【分析】根据垂直平分线的性质定理，得【详解】解：∵AB 的中垂线交【点睛】本题主要考查垂直平分线的性质定理，掌握垂直平分线的性质定理是解题的关键．线段的垂直平分线上的点到线段的两个端点的距离相等．3．（2023春·广东深圳·七年级校考期末）如图，在ABC 中，DM ，EN 分别垂直平分边AC 和边BC ，交边AB 于M ，N 两点，DM 与EN 相交于点F ．(1)若10cm AB =，求CMN 的周长；(2)若o 65MFN ∠=，则MCN ∠的度数为______°．【答案】(1)10cm(2)50【分析】（1）由线段垂直平分线的性质可得MA MC =，NB NC =，则CMN 的周长CM CN MN AM MN BN AB =++=++=；（2）根据等边对等角可得A MAC ∠=∠，B NCB ∠=∠，根据三角形内角和定理，列式求出FMN FNM ∠+∠，再求出A B ∠∠+，即可求解．【详解】（1）解：∵DM ，EN 分别是AC ，BC 的中垂线∴MA MC =，NB NC=∴CMN C CM MN CN AM MN BN =++=++ AB =10cm =；（2）由（1）得MA MC =，NB NC =，由DM ，EN 分别垂直平分AC 和BC ，可得90MDA NEB ∠=∠=︒，∴A MCA ∠=∠，B NCB ∠=∠，∵在MNF 中，65MFN ∠=︒，∴115FMN FNM ∠+∠=︒，根据对顶角的性质可得：FMN AMD ∠=∠，FNM BNE ∠=∠，在Rt ADM △中，9090A AMD FMN ∠=︒-∠=︒-∠，在Rt BNE 中，9090B BNE FNM ∠=︒-∠=︒-∠，∴909065A B FMN FNM ∠+∠=︒-∠+︒-∠=︒，∴65MCA NCB ∠+∠=︒，在ABC 中，65A B ∠+∠=︒∴115ACB ∠=︒，∴()50MCN ACB MCA NCB ∠=∠-∠+∠=︒．故答案为：50．【点睛】本题考查了线段垂直平分线的性质，等边对等角的性质，三角形内角和定理，解题的关键是熟练掌握相关基本性质和整体思想的利用．【考点二线段垂直平分线的判定】例题：（2023春·陕西西安·七年级校考阶段练习）如图，AD 为三角形ABC 的角平分线，DE AB ⊥于点E ，DF AC ⊥于点F ，连接EF 交AD 于点O ．(1)若BE DE =，60BAC ∠=︒，求CDF ∠的度数；(2)写出AD 与EF 的关系，并说明理由；【答案】(1)15︒(2)AD EF ⊥，AD 平分EF【分析】（1）根据三角形内角和可得C ∠，再利用内角和即可得出CDF ∠；（2）由角平分线的意义及两个垂直可证明ADE ADF V V ≌，从而有,AE AF DE DF ==，由线段垂直平分线的判定知，AD EF ⊥，AD 平分EF ．【详解】（1）解：∵DE AB⊥90BED ∴∠=︒∵BE DE=45B ∴∠=︒∵60BAC ∠=︒180456075C ∴∠=︒-︒-︒=︒∵DF AC⊥90DFC ∴∠=︒∴15CDF ∠=︒（2）解：AD EF ⊥，AD 平分EF ；理由如下：∵AD 平分BAC ∠，∴∠=∠DAB DAC ，∵DE AB ⊥，DF AC ⊥，∴90DEA DFA ∠=∠=︒，∵AD AD =，∴ADE ADF V V ≌，∴AE AF DE DF ==，，∴AD 是线段EF 的垂直平分线，即AD EF ⊥，AD 平分EF ．【点睛】本题考查了全等三角形的证明，等腰三角形的性质，三角形内角和，角平分线的性质．找到Rt AED △和Rt ADF ，通过两个三角形全等，找到各量之间的关系，完成证明是关键．【变式训练】1．（2023秋·广西河池·八年级统考期末）如图，在ABC 中，边AB ，BC 的垂直平分线交于点P ．(1)求证：PA PB PC ==；(2)求证：点P 在线段AC 的垂直平分线上．【答案】(1)见解析(2)见解析【分析】（1）根据垂直平分线的性质直接可得到答案；（2）根据到线段两个端点的距离相等的点在线段的垂直平分线上即可得到答案；【详解】（1）证明：∵边AB 、BC 的垂直平分线交于点P ，∴PA PB =，PB PC =，∴PA PB PC ==；（2）证明：∵边AB ，BC 的垂直平分线交于点P ，∴PA PB =，PB PC =，∴PA PC =，∴点P 在AC 的垂直平分线上．【点睛】本题考查垂直平分线的性质及判定，解题的关键是熟练掌握垂直平分线上的点到线段两个端点距离相等及到线段两个端点的距离相等的点在线段的垂直平分线上．2．（2023春·全国·八年级专题练习）如图，点D 是等边ABC 外一点，120BDC ∠=︒，DB DC =，点E ，F 分别在AB ，AC 上，连接AD 、DE 、DF 、EF ．(1)求证：AD 是BC 的垂直平分线；(2)若ED 平分BEF ∠，5BC =，求AEF △的周长．【答案】(1)见解析；(2)10．【分析】（1）根据到线段两端距离相等的点在垂直平分线上即可证明；（2）如图，过D 作DM EF ⊥于M ，结合已知易证90DBE ∠=︒即DB AB ⊥，同理可得DC AC ⊥，易证()Rt DBE Rt DME HL ≌得BE ME =，同理可得CF MF =，然后转换求周长即可．【详解】（1）证明：ABC 是等边三角形，AB AC ∴=，∴A 在BC 的垂直平分线上，又DB DC =，∴D 在BC 的垂直平分线上，AD ∴是BC 的垂直平分线；（2）如图，过D 作DM EF ⊥于M ，120BDC ∠=︒ ，DB DC=30DBC ∴∠=︒又ABC 是等边三角形，90DBE DBC ABC ∴∠=∠+∠=︒A DB B∴⊥同理可得DC AC∴⊥ED 平分BEF ∠，DM EF⊥DB DM DC∴==DF ∴平分CFE ∠，在Rt DBE 与Rt DME 中DE DE DB DM=⎧⎨=⎩()Rt DBE Rt DME HL ∴ ≌BE ME∴=同理可得CF MF=()AEF C AE AF EF AE AF EM MF =++=+++ ()AE AF EB CF =+++()()AE EB AF CF =+++AB AC=+210BC ==.【点睛】本题考查了垂直平分线的判定，角平分线的判定和性质，全等三角形的判定和性质；解题的关键是通过相关性质构造线段相等、进行转换．【考点三利用角平分线的性质求解】A ．14B ．26【答案】D 【分析】如图：作DF AC ⊥交∵AD 平分BAC ∠，DE AB ⊥∴4DF DE ==，∴12ABC ADC ADB S S S AC ==+ 【变式训练】1．（2023春·甘肃张掖·八年级校考期末）一块三角形的草坪，现要在草坪上建一个凉亭供大家休息，要使凉亭到草坪三边的距离相等，凉亭的位置应选在（）A ．三角形三条边的垂直平分线的交点B ．三角形三条角平分线的交点C ．三角形三条高所在直线的交点D ．三角形三条中线的交点【答案】B【答案】5【分析】根据垂线段最短确定点【详解】解： O是BA上任意一点，∴当PO BA⊥时，OP的值最小，∠，P是BD又 BD平分ABC(1)求PAD∠的度数；=．(2)试说明PD PC∵AP 平分DAB ∠，PD AD ⊥，PE ∴PE PD =．∵BP 平分ABC ∠，PC BC ⊥，PE ∴PE PC =，【考点四角平分线的判定】例题：（2023·全国·八年级假期作业）如图，ABC ∠的平分线与ACB ∠的外角平分线相交于点D ，连接AD ．求证：AD 是BAC ∠的外角平分线．【答案】证明见解析【分析】作DE BA ⊥交BA 的延长线于E ，DF AC ⊥于F ，DG BH ⊥于G ，根据角平分线的性质得到DE DF =，根据角平分线的判定定理证明结论．【详解】证明：作DE BA ⊥交BA 的延长线于E ，DF AC ⊥于F ，DG BH ⊥于G ，DB 平分ABC ∠、DC 平分ACH ∠，DE DG ∴=，DF DG =，DE DF ∴=，又DE BA ⊥，DF AC ⊥，∴AD 是BAC ∠的外角平分线．【点睛】本题考查的是角平分线的性质和判定，掌握角的平分线上的点到角的两边的距离相等、到角的两边的距离相等的点在角的平分线上是解题的关键．【变式训练】1．（2023·广东惠州·校联考二模）如图，CB CD =，180D ABC ∠+∠=︒，CE AD ⊥于E ．(1)求证：AC 平分DAB ∠；(2)若10AE =，4DE =，求AB 的长．【答案】(1)见解析(2)6【分析】（1）过C 点作CF AB ⊥，交AB 的延长线于点F ．由AAS 证明CDE CBF ≌，可得CE CF =，结论得证；（2）证明Rt ACE Rt ACF ≌，可得AE AF =，可求出AB ．【详解】（1）证明：过C 点作CF AB ⊥，交AB 的延长线于点F ．∵CE AD ⊥，∴90DEC CFB ∠=∠=︒，∵180D ABC ∠+∠=︒，180CBF ABC ∠+∠=︒，∴D CBF ∠=∠，又∵CB CD =，∴CDE CBF ≌，∴CE CF =，∴AC 平分DAB ∠；（2）解：由（1）可得4BF DE ==，在Rt ACE 和Rt ACF 中，CE CF AC AC=⎧⎨=⎩，∴Rt ACE Rt ACF ≌，∴10==AE AF ，∴6AB AF BF =-=．【点睛】本题考查了角平分线的判定与性质，全等三角形的判定与性质，关键是作出辅助线构造全等三角形．2．（2023·江苏·八年级假期作业）如图，DE AB ⊥于点E ，DF AC ⊥于点F ，若,BD CD BE CF ==．(1)求证：AD 平分BAC ∠；(2)请猜想+AB AC 与AE 之间的数量关系，并给予证明．【答案】(1)见解析(2)2AB AC AE +=，证明见解析【分析】（1）根据HL 证明Rt Rt DBE DCF ≌ ，得到DE DF =，再根据角平分线的判定定理，求证即可；（2）通过HL 证明Rt Rt ADE ADF ≌△△，得到AE AF =，利用线段之间的关系，求解即可．【详解】（1）证明：∵DE AB ⊥，DF AC ⊥，∴90E DFC ∠=∠=︒，在Rt DBE 和Rt DCF 中，BD CD BE CF =⎧⎨=⎩，∴()Rt Rt HL DBE DCF ≌△△，∴DE DF =，∵DE AB ⊥，DF AC ⊥，∴AD 平分BAC ∠．（2）解：2AB AC AE +=，证明如下：在Rt ADE △和Rt ADF 中，AD AD DE DF=⎧⎨=⎩，∴()Rt Rt HL ADE ADF ≌△△，∴AE AF =，∴2AB AC AB AF CF AB AE BE AE +=++=++=．【点睛】此题考查了全等三角形的判定与性质，以及角平分线的判定定理，解题的关键是灵活利用相关性质进行求解．【考点五线段的垂直平分线与角平分线的综合问题】例题：（2023秋·河北保定·八年级统考期末）如图，在ABC 中，AD 平分BAC ∠，90C = ∠，DE AB ⊥于点E ，点F 在AC 上，BD DF =．(1)求证：CF EB =．(2)连接CE ，求证AD 垂直平分CE ．(3)若10AB =，6AF =，求CF 的长．【答案】(1)证明见解析(2)证明见解析(3)2CF =【分析】（1）利用角平分线的性质可得DC DE =，再利用“HL ”证明t R DCF Rt DEB △≌△，即可证明CF EB =；（2）利用“HL ”证明Rt ACD Rt AED ≌，可得AC AE =，所以点A 在CE 的垂直平分线上，根据DC DE =，可得点D 在CE 的垂直平分线上，进而可以解决问题；（3）设CF BE x ==，则AE AB BE x AC AF FC x 106=-=-==+=+，即可建立方程求解．【详解】（1）证明：∵DE AB ⊥于点E ，∴90DEB ∠= ，又AD 平分BAC ∠，90C = ∠，∴DC DE =，在t R DCF △和Rt DEB 中，DF DB DC DE =⎧⎨=⎩，∴()t R DCF Rt DEB HL ≌，∴CF EB =．（2）证明：连接CE ，如图在Rt ACD 和Rt AED △中，AD AD DC DE =⎧⎨=⎩，∴()Rt ACD Rt AED HL ≌，∴AC AE =∴点A 在CE 的垂直平分线上，∵DC DE =，∴点D 在CE 的垂直平分线上，∴AD 垂直平分CE （3）解：设CF BE x ==，∵10AB =，6AF =，∴AE AB BE x 10=-=-，AC AF FC x 6=+=+，∵AE AC =，∴106x x -=+，解得：2x =∴2CF =【点睛】本题考查了直角三角形全等的判定与性质，角平分线的性质，解题关键是在图形中找到正确的全等三角形以及熟悉以上性质与判定．【变式训练】1．（2023秋·河南洛阳·八年级统考期末）如图，AD 是ABC 的角平分线，DE AB ⊥于点E ，DF AC ⊥于点F ，连接EF ．(1)求证：AD 为CAB ∠的角平分线；(2)若8AB =，6AC =，求AE 的长．【答案】(1)见解析(2)7AE =DG 为BC 的垂直平分线，CD BD ∴=，DE AB ∵⊥，DF AC ⊥，90DEB DFC ∴∠=∠=︒，在Rt DEB △和Rt DFC △中，(1)求证：BD平分∠ABC；(2)如图2，AC的垂直平分线交BD于点Q，交AC于点G，QM 【答案】(1)见解析(2)MC=1.5【分析】（1）由∠ACF=∠A+∠ABF，∠ECF=∠BPC+∠DBF，得∠【详解】（1）证明：∵∠ACF=∠A+∠ABF，∠ECF=∠BPC+∠DBF，∴∠ABF=∠ACF-78°，∠DBF=∠ECF-39°，∵CE平分∠ACF，∴∠ACF=2∠ECF，∴∠ABF=2∠ECF-78°=2（∠ECF-39°）=2∠DBF，∴BD平分∠ABC；（2）解：连接AQ，CQ，过点Q作BA的垂线交BA的延长线于N，∵QG垂直平分AC，∴AQ=CQ，∵BD平分∠ABC，QM⊥BC，QN⊥BA，∴QM=QN，∴Rt△QNA≌Rt△QMC（HL），∴NA=MC，∵QM=QN，BQ=BQ，∴Rt△QNB≌Rt△QMB（HL），∴NB=MB，∴BC=BM+MC=BN+MC=AB+AN+MC，∴7=4+2MC，∴MC=1.5．【点睛】本题主要考查了角平分线的定义和性质，三角形外角的性质，线段垂直平分线的性质，全等三角形的判定与性质等知识，作辅助线构造全等三角形是解题的关键．【过关检测】一、选择题1．（2023春·四川成都·八年级统考期末）如图，在ABC 中，DE 是AC 边的垂直平分线，分别交BC AC 、于D 、E 两点，连接AD ，25BAD ∠=︒，35C ∠=︒，则B ∠的度数为（）A ．70︒B ．75︒C ．80︒D ．85︒【答案】D 【分析】利用垂直平分线的性质，可得35DAC C ∠=∠=︒，根据三角形内角和定理，可得B ∠的度数．【详解】解：DE 是AC 边的垂直平分线，35DAC C ∴∠=∠=︒，根据三角形内角和定理，可得18085B BAD DAC C ∠=︒-∠-∠-∠=︒，故选：D ．【点睛】本题考查了垂直平分线的性质，三角形内角和定理，熟练利用垂直平分线的性质是解题的关键．2．（2023春·四川达州·八年级统考期末）如图，点P 为定角AOB ∠平分线上的一个定点，且MPN ∠与AOB ∠互补．若MPN ∠在绕点P 旋转的过程中，其两边分别与OA 、OB 相交于M 、N 两点，则以下结论中，不正确的是（）A ．OM ON +的值不变C ．MN 的长不变【答案】C 【分析】如图作PE OA ⊥于E ∠∠EPM FPN =，由OP 平分∵∠∠90PEO PFO ==︒，∴∠∠180EPF AOB +=︒，∵∠∠180MPN AOB +=︒，∴∠∠MPN EPF =，∴∠∠EPM FPN =，∠故选：C【点睛】本题主要考查角平线的性质定理、全等三角形的判定和性质；能够结合角平分线的性质定理作出角平分线上点到两边的垂线段，构建全等三角形是解题的关键．二、填空题【答案】6【分析】过点C 作CP AB ⊥再根据三角形的面积公式求出【详解】解：过点C 作CP ∵BD 平分ABC ∠，PE AB ⊥∴PE EF =，∴CP CE PE CE EF =+=+的最小值．∵ABC 的面积为18，AB =性，是一道比较好的题目．三、解答题(1)如图1，若DE OB ∥．①DEO ∠的度数是︒，当DP OE ⊥时，x =②若EDF EFD ∠=∠，求x 的值；(2)如图2，若DE OA ⊥，是否存在这样的x 的值，使得说明理由．②∵20DEO ∠=︒，EDF EFD ∠=∠，∴80EDF ∠=︒，又∵140ODE ∠=︒，∴1408060ODP ∠=︒-︒=︒，∴60x =；（2）存在这样的x 的值，使得4EFD EDF ∠=∠．分两种情况：①如图2，若DP 在DE 左侧，∵DE OA ⊥，∴90EDF x ∠=︒-︒，∵20AOC ∠=︒，∴20EFD x ∠=︒+︒，当4EFD EDF ∠=∠时，()20490x x ︒+︒=︒︒﹣，解得68x =；②如图3，若DP 在DE 右侧，∵90EDF x ∠=︒-︒，18020160EFD x x ∠=︒-︒-︒=︒-︒，∴当4EFD EDF ∠=∠时，()160490x x ︒-︒=︒-︒，解得104x =；综上所述，当68x =或104时，4EFD EDF ∠=∠．(1)如图1，求BGC ∠的度数；(2)如图2，求证：EG FG =；(3)如图3，过点C 作CD EC ⊥交BF 延长线于点D ，连接AD ，点N 在BA 延长线上，连接NG 交AC 于点M 使DAC NGD ∠=∠，若:1:2EB FC =，10CG =，求线段MN 的长．【答案】(1)120︒(2)见解析∴60BGH CGH ∠=∠=︒，∵60BGE CGF GBC GCB ∠=∠=∠+∠=∴G BGH C CG GH B E F ∠∠=∠=∠=，∵GBC GBE ∠=∠，BG BG=∴BGE BGH ≌△△，∴EG GH =，∵CE 平分ACB ∠，∴2ACB ACE ∠=∠，∵CD EC ⊥，∴90ECD ∠=︒，∴90ACE ACD ∠+∠=︒，∵180ACB ACP ∠+∠=︒，∴2ACP ACD ∠=∠，∴CD 平分ACP ∠，∵DR AC ⊥，DP BC ⊥，∴DR DP =，∵BF 平分ABC ∠，DR AC ⊥，DQ AB ⊥，∴DP DQ =，∴DR DQ =，∴AD 平分QAC ∠，∵60BAC ∠=︒，∴60DAQ DAC ∠=∠=︒，∴60NGD DAC ∠=∠=︒，由（1）得120BGC ∠=︒，∴18060BEG FGC BGC ∠=∠=︒-∠=︒，∵60MGF ABF BNG ∠=∠+∠=︒，60FGC FBC ECB ∠=∠+∠=︒，(1)如图1，请指出AB 与PB 的数量关系，并说明理由．(2)如图2，当P ，Q 两点都在射线ON 的反向延长线上时，线段AB ，PB 是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由．【答案】(1)AB PB =，理由见解析(2)存在，理由见解析【分析】（1）连接BQ ，根据BC 垂直平分OQ ，可知BO BQ =，则BOQ BQO ∠=∠，根据OF 平分MON ∠，则AOB BOQ ∠=∠，即AOB BQO ∠=∠，根据OA QP =，可知AOB PQB △≌△，则可知AB PB =；（2）如图，连接BQ ，根据BC 垂直平分OQ ，可知BQ BO =，CQ CO =结合条件可证BQC BOC △≌△，则BQO BOQ ∠=∠，根据OF 平分MON ∠，BOQ FON =∠∠，可知AOF FON BOQ ∠=∠=∠，则AOF BQO =∠∠，进而可知AOB PQB =∠∠，由此可证AOB PQB △≌△（SAS ），则AB PB =．【详解】（1）解：AB PB=理由如下：连接BQ∵BC 垂直平分OQ∴BO BQ=∴BOQ BQO∠=∠∵OF 平分MON∠∴AOB BOQ∠=∠∴AOB BQO∠=∠∵OA QP=∴AOB PQB△≌△∴AB PB =；（2）存在，理由：如图，连接BQ ，∵BC 垂直平分OQ ，∴BQ BO =，CQ CO=在BQC 和BOC 中，BC BC CQ CO BQ BO =⎧⎪=⎨⎪=⎩∴BQC BOC △≌△（SSS ）∴BQO BOQ ∠=∠，∵OF 平分MON ∠，BOQ FON =∠∠，∴AOF FON BOQ ∠=∠=∠，∴AOF BQO =∠∠，∴AOB PQB =∠∠，在△AOB 和△PQB 中，OA PQ AOB PQB BO BQ =⎧⎪∠=∠⎨⎪=⎩【知识回顾】（1）如图1，P 是BOA ∠的平分线上的一点，PE OB ⊥于点E ，作PD OA ⊥于点D ，试证：【深入探究】（2）如图2，在ABC 中，BD 为ABC ∠的角平分线交于AC 于D 点，其中10,AB BC AD +=BD Q 平分BAC ∠，DM DN ∴=，11,22ABD CBD S AB DM S BC =⋅= ABD S AB S BC∴= ，∴BC∥EF由①知：∠CBP＝90°∴BP⊥EF∵EB＝EP∴EF是线段BP的垂直平分线∴PF＝BF∴∠PFE＝∠BFE＝30°（2）如图2，延长DE到Q，使EQ＝DE，连接CD，PQ，FQ∵EC＝EP，∠DEC＝∠QEP∴△QEP≌△DEC（SAS）则PQ＝DC＝DB∵QE＝DE，∠DEF＝90°∴EF是DQ的垂直平分线∴QF＝DF∵CD＝AD∴∠CDA＝∠A＝60°∴∠CDB＝120°∴∠FDB＝120°﹣∠FDC＝120°﹣（60°+∠EDC）＝60°﹣∠EDC＝60°﹣∠EQP＝∠FQP ∴△FQP≌△FDB（SAS）∴∠QFP＝∠BFD∵EF是DQ的垂直平分线∴∠QFE＝∠EFD＝30°(1)【理解运用】如图2，在ABC 中，D 为BC 上一点，点D ，E 关于直线AB 对称，连接判断点B 是否为点D ，F 关于直线AB 的“等角点”，并说明理由；(2)【拓展提升】如图2，在（1）的条件下，若70A ∠=︒，AB AC =，点Q 是射线EF 上一点，且点D ，Q 角点”为点C ，请利用尺规在图2中确定点Q 的位置，并求出BQC ∠的度数；(3)【拓展提升】∵D 、E 关于AB 对称，∴BE BD =，AB DE ⊥，∴ABE ABC ∠=∠，∵ABE MBF Ð=Ð，∴ABC MBF Ð=Ð，∴点B 是点D ，F 关于直线AB 的“等角点”；（2）如图2，∵70A ∠=︒，AB AC =，∴55ABC ACB ∠=∠=︒．∵点D ，Q 关于直线AB ，AC 的“等角点”分别为点B 和点C ，∴55MBQ NCQ ∠=∠=︒，∴70CBQ BCQ ∠=∠=︒，∴40BQC ∠=︒；（3）如图3，。

2021年中考数学专题16 角平分线与线段的垂直平分线（基础巩固练习，共30个小题）一、选择题（共15小题）：1.（2020•怀化）在Rt△ABC中，∠B＝90°，AD平分∠BAC，交BC于点D，DE⊥AC，垂足为点E，若BD＝3，则DE的长为（）C．2 D．6A．3 B．322.（2019•兴安盟）如图，BD是△ABC的角平分线，DE是BC的垂直平分线，∠BAC＝90°，AD＝3，则CD的长为（）A．3√3B．6 C．5 D．43.（2019•陕西）如图，在△ABC中，∠B＝30°，∠C＝45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E．若DE＝1，则BC的长为（）A．2+√2B．√2+√3C．2+√3D．34.（2019•张家界）如图，在△ABC中，∠C＝90°，AC＝8，DC=13AD，BD平分∠ABC，则点D到AB的距离等于（）A．4 B．3 C．2 D．15.（2019•湖州）如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是（）A．24 B．30 C．36 D．426.（2018•辽阳）如图，在∠MON中，以点O为圆心，任意长为半径作弧，交射线OM于点A，交射线ON于点B，再分别以A，B为圆心，OA的长为半径作弧，两弧在∠MON 的内部交于点C，作射线OC．若OA＝5，AB＝6，则点B到AC的距离为（）A．5 B．245C．4 D．1257.（2018•梧州）如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，DE＝6，则DF的长度是（）A．2 B．3 C．4 D．68.（2018•大庆）如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC，且∠ADC＝110°，则∠MAB＝（）A．30°B．35°C．45°D．60°9.（2018•常德）如图，已知BD是△ABC的角平分线，ED是BC的垂直平分线，∠BAC＝90°，AD＝3，则CE的长为（）A．6 B．5 C．4 D．3√310.（2020•益阳）如图，在△ABC中，AC的垂直平分线交AB于点D，CD平分∠ACB，若∠A＝50°，则∠B的度数为（）A．25°B．30°C．35°D．40°11.（2020•宜昌）如图，点E，F，G，Q，H在一条直线上，且EF＝GH，我们知道按如图所作的直线l为线段FG的垂直平分线．下列说法正确的是（）A．l是线段EH的垂直平分线 B．l是线段EQ的垂直平分线C．l是线段FH的垂直平分线 D．EH是l的垂直平分线12.（2020•枣庄）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为（）A．8 B．11 C．16 D．1713.（2019•梧州）如图，DE是△ABC的边AB的垂直平分线，D为垂足，DE交AC于点E，且AC＝8，BC＝5，则△BEC的周长是（）A．12 B．13 C．14 D．1514.（2019•南充）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC＝6，AC＝5，则△ACE的周长为（）A．8 B．11 C．16 D．1715.（2018•南通）如图，Rt△ABC中，∠ACB＝90°，CD平分∠ACB交AB于点D，按下列步骤作图：步骤1：分别以点C和点D为圆心，大于12CD的长为半径作弧，两弧相交于M，N两点；步骤2：作直线MN，分别交AC，BC于点E，F；步骤3：连接DE，DF．若AC＝4，BC＝2，则线段DE的长为（）A．53B．32C．√2D．43二、填空题（共10小题）：16.（2020•湘潭）如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD＝3，点M是射线OC上一动点，则PM的最小值为．17.（2019•永州）已知∠AOB＝60°，OC是∠AOB的平分线，点D为OC上一点，过D作直线DE⊥OA，垂足为点E，且直线DE交OB于点F，如图所示．若DE＝2，则DF＝．18.（2020•十堰）如图，在△ABC中，DE是AC的垂直平分线．若AE＝3，△ABD的周长为13，则△ABC的周长为．19.（2020•南京）如图，线段AB、BC的垂直平分线l1、l2相交于点O，若∠1＝39°，则∠AOC＝．20.（2020•青海）如图，△ABC中，AB＝AC＝14cm，AB的垂直平分线MN交AC于点D，且△DBC的周长是24cm，则BC＝cm．21.（2018•南充）如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B＝70°，∠FAE＝19°，则∠C＝度．22.（2019秋•澧县期末）如图，已知AB＝AC，AB的垂直平分线MN交AB于点E，交AC于点D，若∠A＝38°，则∠BDE＝．23.（2020•武汉模拟）如图，△ABC中，DE是BC的垂直平分线，CE是∠ACB的平分线，FG为△ACE的中位线，连DF，若∠DFG＝108°，则∠AED＝．24.（2020秋•涪城区校级期末）如图，∠BAC与∠CBE的平分线相交于点P，BE＝BC，PB与CE交于点H，PG∥AD交BC于F，交AB于G，下列结论：①GA＝GP；②S△PAC：S △PCB＝AC：CB；③BP垂直平分CE；④CP＝FC，其中正确的判断有．（填序号）25.（2018•锦州）如图，射线OM在第一象限，且与x轴正半轴的夹角为60°，过点D（6，0）作DA⊥OM于点A，作线段OD的垂直平分线BE交x轴于点E，交AD于点B，作射线OB，以AB为边在△AOB的外侧作正方形ABCA1，延长A1C交射线OB于点B1，以A1B1为边在△AOB的外侧作正方形A1B1C1A2，延长A2C1交射线OB于点B2，以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3…按此规律进行下去，则正方形A2017B2017C2017A2018的周长为．三、解答题（共5小题）：26.（2020秋•庐阳区期末）如图，△ABC中，∠BAC＝100°，∠C＝50°，AD⊥BC，垂足为D，EF是边AB的垂直平分线，交BC于E，交AB于点F，求∠EAD的度数．27.（2020•香洲区二模）如图，在Rt△ABC中，∠ACB＝90°，AC＞BC．（1）请用尺规作图法，作边AB的垂直平分线交AC于点D（不要求写作法，但保留作图痕迹）；（2）若AC＝4，AB＝5，连接BD，求△BCD的周长．28.（2020•临清市一模）如图，矩形ABCD中，对角线AC的垂直平分线EF分别交AC，BC，AD于点O，E，F．（1）求证：AF＝CE；（2）若BE＝3，AF＝5，求AC的长．29.（2020•南岗区三模）已知：在△ABC中，AC＜AB＜BC．线段AB的垂直平分线交BC于点D，点E在BC上，且BE＝AB．连接AD，AE，∠AEC＝3∠BAD．（1）如图1，求证：AD＝AE；（2）如图2，当∠B＝2∠CAE时，在不添加任何辅助线情况下，请直接写出图2中的四个等腰三角形．30.（2020•金牛区模拟）如图，点E在矩形ABCD对角线AC上由A向C运动，且BC＝2√3，∠ACB＝30°，连结EF，过点E作EF⊥DE，交BC于点F（当点F与点C重合时，点E 也停止运动）（1）如图1，当AC平分角∠DEF时，求AE的长度；（2）如图2，连结DF，与AC交于点G，若DF⊥AC时，求四边形DEFC的面积；（3）若点E分AC为1：2两部分时，求BF：FC．。