专题三中考数学动点最值

动点最值问题永远都是中考最难的压轴类题目，很多同学都反应不知道该怎么下手寻找思路。

其实这类题目的题型有限，全部总结归纳就是这19种，希望同学们对每一种都能掌握技巧，再遇见类似的就能及时找到思路。

PS：可下载电子版打印高清版本，链接文末获取！
1、将军饮马模型（对称点模型）
2、利用三角形两边差求最值
3、手拉手全等取最值
4、手拉手相似取最值
5、平移构造平行四边形求最小
6、两点对称勺子型连接两端求最小
7、两点对称折线连两端求最小
8、时钟模型，中点两定边求最小值
9、时钟模型，相似两定边求最小值
10、转化构造两定边求最值
11、面积转化法求最值
12、相似转化法求最值
13、相似系数化一法求最值
14、三角函数化一求最值
15、轨迹最值
16、三动点的垂直三角形
17、旋转最值
18、隐圆最值-定角动弦
19、隐圆最值-动角定弦。

培优冲刺03 几何最值类问题综合本考点是中考五星高频考点，难度中等偏上，在全国很多地市的中考试卷中多有考查。

（2022年柳州中考试卷第18题）如图，在正方形ABCD中，AB＝4，G是BC的中点，点E是正方形内一个动点，且EG＝2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值为．【分析】连接DG，将DG绕点D逆时针旋转90°得DM，连接MG，CM，MF，作MH ⊥CD于H，利用SAS证明△EDG≌△DFM，得MF＝EG＝2，再说明△DGC≌△DMH （AAS），得CG＝DH＝2，MH＝CD＝4，求出CM的长，再利用三角形三边关系可得答案．【解答】解：方法一：连接DG，将DG绕点D逆时针旋转90°得DM，连接MG，CM，MF，作MH⊥CD于H，∵∠EDF＝∠GDM，∴∠EDG＝∠FDM，∵DE＝DF，DG＝DM，∴△EDG≌△MDF（SAS），∴MF＝EG＝2，∵∠GDC＝∠DMH，∠DCG＝∠DHM，DG＝DM，∴△DGC≌△MDH（AAS），∴CG＝DH＝2，MH＝CD＝4，∴CM＝＝2，∵CF≥CM﹣MF，∴CF的最小值为2﹣2，方法二：连接AG、AE，由方法一同理得，AE＝CF，AG＝2，∵AE≥AG﹣EG＝2﹣2，∴AE的最小值为2﹣2，∴CF的最小值为2﹣2，故答案为：2﹣2．点评：本题主要考查了正方形的性质、旋转的性质、全等三角形的判定和性质，勾股定理，三角形三边关系等知识，做辅助线构造全等三角形是解题的关键。

初中数学中，几何最值问题属于难度较大的一类题，问题环境可以是三角形、四边形、圆或者反比例函数、二次函数。

而常用到的最值原理则有：两点之间线段最短（三点共线）、点到直线的距离垂线段最短、圆和圆外定点的最值原理等。

这类题的原理虽然较为固定，但对学生的逻辑思维能力要求较高，综合型较强。

本考点是中考五星高频考点，难度较大，个别还会以压轴题出现，在全国多地市的中考试卷中多有考查。

中考数学中关于动点的最值问题作者：邓昌滨来源：《中学数学杂志(初中版)》2008年第05期在平面几何问题中，当某点在给定条件运动时，求某几何量的最大值或最小值问题，即最值问题. 这类题综合性强，能力要求高. 它能全面的考查学生的实践操作能力、空间想象能力以及分析问题和解决问题的能力，对培养学生的思维品质和各种能力有更大的促进作用，本文仅以2008年江苏中考压轴题为例进行分析，供参考.1 利用函数的性质求最值图1例1 （2008年连云港）如图1，现有两块全等的直角三角形纸板Ⅰ、Ⅱ，它们两直角边的长分别为1和2. 将它们分别放置于平面直角坐标系中的△AOB，△COD处，直角边OB，OD在x轴上. 一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动. 当纸板Ⅰ移动至△PEF处时，设PE，PF与OC分别交于点M，N，与x轴分别交于点G，H.（1）求直线AC所对应的函数关系式；（2）当点P是线段AC（端点除外）上的动点时，试探究：①点M到x轴的距离h与线段BH的长是否总相等？请说明理由；②两块纸板重叠部分（图中的阴影部分）的面积S是否存在最大值？若存在，求出这个最大值及S取最大值时点P的坐标；若不存在，请说明理由.解（1）由直角三角形纸板的两直角边的长为1和2，知A，C两点的坐标分别为（1，2），（2，1）. 易得直线AC所对应的函数关系式为y=-x+3.①点M到x轴的距离h与线段BH的长总相等. 因为点C的坐标为（2，1），所以，直线OC所对应的函数关系式为y=12x. 又因为点P在直线AC上，所以可设点P的坐标为（a,3-a). 过点M作x轴的垂线，设垂足为点K，则有MK=h. 因为点M在直线OC上，所以有M(2h,h). 因为纸板为平行移动，易得Rt△PHG∽△Rt△PFE,有GHPH=EFPF=12. 故GH=12PH=12(3-a). 所以OG=OH-GH=a-12(3-a)=32(a-1). 故G点坐标为(32(a-1),0). 又点P的坐标为(a,3-a),可得直线PG所对的函数关系式为y=2x+(3-3a). 将点M的坐标代入，得h=4h+(3-3a).解得h=a-1. 而BH=OH-OB=a-1，从而总有h=BH.②由①知，点M的坐标为(2a-2,a-1)，点N的坐标为(a,12a).△-△-12OG×h=12×12a×a-12×3a-32×(a-1)=--34=-12(a-当a=32时，S有最大值，最大值为38.取最大值时点P的坐标为(32,32).评注解此类题的关键是分析运动变化的过程，用点P的横坐标a的代数式表示描述点的运动过程，把动点视为静点参与运算，列出关于a的函数关系式，证明线段相等，再根据二次函数的增减性求得最值问题.2 利用轴对称变换求最值图2例2 （2008年南通）如图2，四边形ABCD中，AD=CD，∠DAB=∠ACB=90°，过点D 作DE⊥AC，垂足为F，DE与AB相交于点E.（1）求证：AB•AF=CB•CD；（2）已知AB=15cm,BC=9cm，P是射线DE上的动点. 设DP=xcm(x>0),四边形BCDP 的面积为①求y关于x的函数的关系式；②当x为何值时，△PBC的周长最小，并求出此时y的值.证明（1）因为AD=CD，DE⊥AC，所以DE垂直平分AC，所以AF=CF，∠DFA=∠DFC=90°，∠DAF=∠DCF. 因为∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°，所以∠DCF=∠DAF=∠B,易得△DCF∽△ABC,所以CDAB=CFCB,即CDAB=AFCB. 所以AB•AF=CB•CD.解（2）①因为AB=15，BC=9，∠ACB=90°，所以--所以CF=AF=6，所以y=12(x+9)×6=3x+27(x>0).②因为BC=9（定值），所以△PBC的周长最小，就是PB+PC最小. 由（1）可知，点C 关于直线DE的对称点是点A，所以PB+PC=PB+PA，故只要求PB+PA最小. 显然当P、A、B 三点共线时PB+PA最小. 此时DP=DE，PB+PA=AB. 由（1），∠ADF=∠FAE，∠DFA=∠ACB=90°，得△DAF∽△ABC. EF∥BC,得AE=BE=12AB=152,EF=92，所以AF∶BC=AD∶AB,即6∶9=AD∶15，所以AD=10. Rt△ADF中，AD=10，AF=6，所以DF=8. 所以DE=DF+FE=8+92=252.所以当x=252时，△PBC的周长最小，此时y=1292.评注本题可转化为直线上一点到直线同侧两点的距离和最小问题，一般我们先用“对称”的方法化成两点之间的最短距离问题，然后根据“两点之间的线段最短”，从而找到所需的最短路线.3 利用动点的范围求最值例3 （2008年徐州）如图，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°.操作将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC交于点Q.探究1 在旋转过程中：（1）如图，当CEEA=1时，EP与EQ满足怎样的数量关系？并给出证明.（2）如图，当CEEA=2时，EP与EQ满足怎样的数量关系？并说明理由.（3）根据你对（1）、（2）的探究结果，试写出当CEEA=m时，EP与EQ满足的数量关系式为，其中m的取值范围是（直接写出结论，不必证明）.图图图探究2 若CEEA=2,AC=30cm,连结PQ，设△EPQ的面积为在旋转过程中：（1）S是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，说明理由.（2）随着S取不同的值，对应△EPQ的个数有哪些变化？求出相应S的取值范围.解探究（1）作EM⊥AB于点M，作EN⊥BC于点N，连结BE，因为∠ABC=90°,所以∠MEN=90°. 因为AB=BC，CE=EA，所以BE为∠ABC的平分线，所以EM=EN. ①若点M、P重合，显然EP=EQ. ②若点M、P不重合，因为∠MEP=∠NEQ=90°-∠PEN，所以Rt△EMP≌Rt△ENQ. 所以（2）作EM⊥AB于点M，作EN⊥BC于点N，因为∠ABC=90°，所以EM∥BC，所以△EMP∽△ENQ,所以EMBC=AEAC=13. 同理ENAB=23. 因为AB=BC，所以EMEN=12. ①若点M、P重合，显然EPEQ=EMEN=12. ②若点M、P不重合，因为∠MEP=∠NEQ=90°-∠PEN，所以△EMP∽△ENQ,所以EPEQ=EMEN=12. 综上，EPEQ=12. 由上可得EPEQ=1m,设EF=x，则DE=AC=3x,当E在边AC上由C向A移动时，要确保EF与BC有交点Q，EQ最大时，EQ⊥BC，此时EQ=EF=x,EC=2x,EA=AC-EC=3x-2x,所以此时m=CEEA=2x3x-2x=6+2,故0探究（1）设EQ=x，则△其中102≤x≤103.故如图，当x=EN=102cm时，△取得最小值如图，当x=EF=103cm时，△取得最大值（2）如图，当x=EB=510cm时，△；故当50时图时图时图评注本题以学生熟悉的三角板为背景，通过学生观察、动手操作、猜想、验证等数学活动过程，激发了学生的学习兴趣，此题的关键是将所求问题转化为动点Q在BC上时EQ的最值问题，渗透了化归、分类、数形结合、特殊化诸多数学思想方法，全面考查了学生的空间想象能力，几何变换，探索问题和解决问题的能力.。

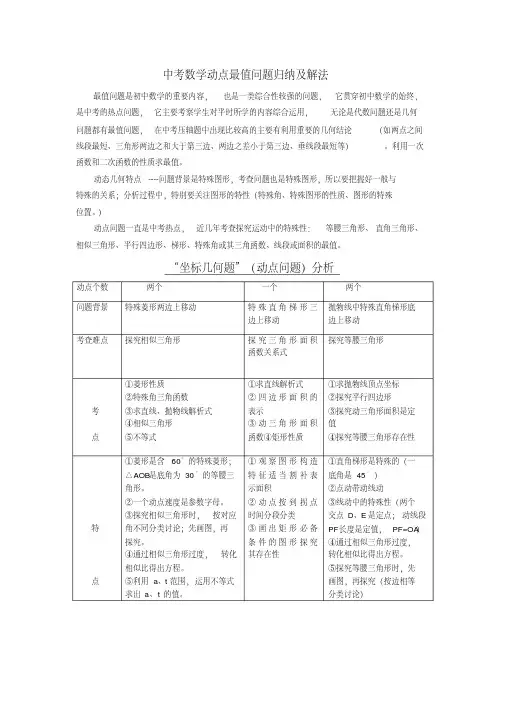
中考数学动点最值问题归纳及解法最值问题是初中数学的重要内容，也是一类综合性较强的问题，它贯穿初中数学的始终，是中考的热点问题，它主要考察学生对平时所学的内容综合运用，无论是代数问题还是几何问题都有最值问题，在中考压轴题中出现比较高的主要有利用重要的几何结论（如两点之间线段最短、三角形两边之和大于第三边、两边之差小于第三边、垂线段最短等）。

利用一次函数和二次函数的性质求最值。

动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

“坐标几何题”（动点问题）分析动点个数两个一个两个问题背景特殊菱形两边上移动特殊直角梯形三边上移动抛物线中特殊直角梯形底边上移动考查难点探究相似三角形探究三角形面积函数关系式探究等腰三角形考点①菱形性质②特殊角三角函数③求直线、抛物线解析式④相似三角形⑤不等式①求直线解析式②四边形面积的表示③动三角形面积函数④矩形性质①求抛物线顶点坐标②探究平行四边形③探究动三角形面积是定值④探究等腰三角形存在性特点①菱形是含60°的特殊菱形；△AOB是底角为30°的等腰三角形。

②一个动点速度是参数字母。

③探究相似三角形时，按对应角不同分类讨论；先画图，再探究。

④通过相似三角形过度，转化相似比得出方程。

⑤利用a、t范围，运用不等式求出a、t的值。

①观察图形构造特征适当割补表示面积②动点按到拐点时间分段分类③画出矩形必备条件的图形探究其存在性①直角梯形是特殊的（一底角是45°）②点动带动线动③线动中的特殊性（两个交点D、E是定点；动线段PF长度是定值，PF=OA）④通过相似三角形过度，转化相似比得出方程。

⑤探究等腰三角形时，先画图，再探究（按边相等分类讨论）近几年共同点：①特殊四边形为背景；②点动带线动得出动三角形；③探究动三角形问题（相似、等腰三角形、面积函数关系式）；④求直线、抛物线解析式；⑤探究存在性问题时，先画出图形，再根据图形性质探究答案。

动点最值问题【考查知识点】“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。

原型----“饮马问题”，“造桥选址问题”。

考的较多的还是“饮马问题”，出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。

【解题思路】找点关于线的对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查.求线段和的最小值需要用到三个基本知识：两点之间，线段最短；轴对称的性质；线段垂直平分线上的点到线段两端点的距离相等.常见情况有三种：“两点一线”型、“一点两线”型和“两点连线” 型.平面上最短路径问题：(1)归于“两点之间的连线中，线段最短”。

凡属于求“变动的两线段之和的最小值”时，大都应用这一模型。

(2)归于“三角形两边之差小于第三边”。

凡属于求“变动的两线段之差的最大值”时，大都应用这一模型。

(3)平面图形中，直线同侧两点到直线上一点距离之和最短问题。

【方法归纳】在平面几何的动态问题中，求几何量的最大值或最小值问题常会运用以下知识：①三角形的三边关系：两边之和大于第三边，两边之差小于第三边；②两点之间线段最短；③连接直线外一点和直线上各点的所有线段中，垂线段最短；④定圆中的所有弦中，直径最长；⑤利用对称的性质求两条线段之和最小的问题，解决此类问题的方法为：如图，要求线段l上的一动点P 到点A、B距离和的最小值，先作点A关于直线L的对称点A′,连接A′B,则A′B与直线L的交点即为P点，根据对称性可知A′B的长即为PA+PB的最小值，求出A′B的值即可.【典型例题】一、将军饮马基础1．如图，周长为16的菱形ABCD中，点E，F分别在边AB，AD上，AE＝1，AF＝3，P为BD上一动点，则线段EP ＋FP 的长最短为( )A ．3B ．4C ．5D ．62．如图，MN 是等边三角形ABC 的一条对称轴，D 为AC 的中点，点P 是直线MN 上的一个动点，当PC+PD 最小时，∠PCD 的度数是( )A ．30°B ．15°C ．20°D ．35°3. 如图：等腰△ABC 的底边BC 长为6，面积是18，腰AC 的垂直平分线EF 分别交AC ，AB 边于E ，F 点．若点D 为BC 边的中点，点M 为线段EF 上一动点，则△CDM 周长的最小值为( )A ．6B ．8C ．9D ．104．如图，等腰三角形ABC 底边BC 的长为4 cm ，面积为12 cm 2，腰AB 的垂直平分线EF 交AB 于点E ，交AC 于点F ，若D 为BC 边上的中点，M 为线段EF 上一点，则△BDM 的周长最小值为( )A ．5 cmB ．6 cmC ．8 cmD ．10 cm二、平面直角坐标系中的最值1．如图，在R t A B O 中，90O B A ∠=︒，()4,4A ，点C 在边A B 上，且13A CC B =，点D 为O B 的中点，点P 为边O A 上的动点，当点P 在O A 上移动时，使四边形P D B C 周长最小的点P 的坐标为( )A ．()2,2B ．55,22⎛⎫ ⎪⎝⎭C ．88,33⎛⎫ ⎪⎝⎭D ．()3,32．在平面直角坐标系中，Rt △AOB 的两条直角边OA 、OB 分别在x 轴和y 轴上，OA=3，OB=4．把△AOB 绕点A 顺时针旋转120°，得到△ADC ．边OB 上的一点M 旋转后的对应点为M′，当AM′+DM 取得最小值时，点M 的坐标为( )A ．(0，335 ) B ．(0，34) C ．(0，35) D ．(0，3)3．直线y ＝x ＋4与x 轴、y 轴分别交于点A 和点B ，点C ，D 分别为线段AB ，OB 的中点，点P 为OA 上一动点，PC ＋PD 值最小时点P 的坐标为( ).A ．(－3，0)B ．(－6，0)C ．(－，0)D ．(－，0)三、双动点最值问题1. 如图，A B C ∆是等边三角形，13A D A B =，点E 、F 分别为边A C 、B C 上的动点，当D E F ∆的周长最小时，F D E ∠的度数是______________.2. 如图，∠AOB=60°，点P是∠AOB内的定点且OP=3，若点M、N分别是射线OA、OB上异于点O 的动点，则△PMN周长的最小值是()A．362B．332C．6 D．33．如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，使△AMN 周长最小时，则∠AMN＋∠ANM的度数为( )A．130°B．120°C．110°D．100°4．如图，四边形ABCD中，∠C=，∠B=∠D=，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF的度数为( )．A．50°B．60°C．70°D．80°四、与圆有关的最值1. 如图，在⊙O中，弦AB=1，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD 的最大值为___．2．如图，已知点A 是以MN 为直径的半圆上一个三等分点，点B 是弧A N 的中点，点P 是半径ON 上的点．若⊙O 的半径为l ，则AP+BP 的最小值为( )A ．2B ．3C ．2D ．1 3．如图，A C 是O 的弦，5A C ＝，点B 是O 上的一个动点，且45A B C ∠︒＝，若点,M N 分别是,A C B C 的中点，则M N 的最大值是_____．五、角平分线有关的最值1．如图，∠AOB ＝60°，点M ，N 分别是射线OA ，OB 上的动点，OP 平分∠AOB ，OP ＝8，当△PMN 周长取最小值时，△OMN 的面积为_____．2．如图，在R t A B C ∆中，90A C B ∠=︒，3A C =，4B C =，A D 是B A C ∠的平分线.若P ，Q 分别是A D 和A C 上的动点，则P C P Q +的最小值是__________.3．如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON的面积为．六、最值与特殊角1．如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N(3，0)是OB上的一定点，点M 是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为______．。

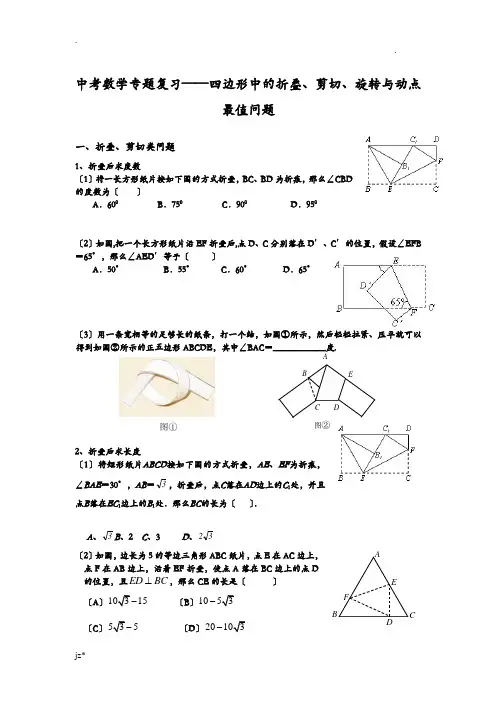
C DEB A 图② 中考数学专题复习——四边形中的折叠、剪切、旋转与动点最值问题一、折叠、剪切类问题1、折叠后求度数〔1〕将一长方形纸片按如下图的方式折叠，BC 、BD 为折痕，那么∠CBD 的度数为〔 〕A ．600B ．750C ．900D ．950〔2〕如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D′、C′的位置，假设∠EFB ＝65°，那么∠AED′等于〔 〕A ．50° B．55° C ．60° D．65°〔3〕用一条宽相等的足够长的纸条，打一个结，如图①所示，然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE ，其中∠BAC ＝____________度.2、折叠后求长度〔1〕将矩形纸片ABCD 按如下图的方式折叠，AE 、EF 为折痕，∠BAE ＝30°，AB ＝3，折叠后，点C 落在AD 边上的C 1处，并且点B 落在EC 1边上的B 1处．那么BC 的长为〔 〕．A 、3B 、2C 、3D 、32〔2〕如图，边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折叠，使点A 落在BC 边上的点D 的位置，且ED BC ⊥，那么CE 的长是〔 〕 〔A 〕10315- 〔B 〕1053-〔C 〕535- 〔D 〕20103-图① ABEF〔3〕如图，将边长为8㎝的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ，那么线段的长是〔 〕 A ．3cmB ．4cmC ．5cmD ．6cm〔4〕如图，将矩形纸ABCD 的四个角向折起，恰好拼成一个无缝隙无重叠的四边形EFGH ，假设EH ＝3厘米，EF ＝4厘米，那么边AD 的长是___________厘米. 〔5〕如图，是一矩形纸片ABCD ，AD =10cm ，假设将纸片沿DE 折叠，使DC 落在DA 上，点C 的对应点为点F ，假设BE =6cm ，那么CD =〔6〕如图〔1〕，把一个长为m 、宽为n 的长方形〔m n >〕沿虚线剪开，拼接成图〔2〕，成为在一角去掉一个小正方形后的一个大正方形，那么去掉的小正方形的边长为〔 〕A ．2m n-B ．m n -C ．2m D ．2n3、折叠后求面积〔1〕如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AE 与BC 交于点F ，那么△CEF 的面积为〔 〕 A ．4 B ．6 C ．8 D ．10〔2〕如图，正方形硬纸片ABCD 的边长是4，点E 、F 分别是AB 、BC 的中点，假设沿左图中的虚线剪开，拼成如下右图的一座“小别墅〞，那么图中阴影局部的面积是〔 〕 NM F E DC B Amn n n〔2〕〔1〕A ．2B ．4C ．8D ．10〔3〕如图a ，ABCD 是一矩形纸片，AB ＝6cm ，AD ＝8cm ，E 是AD 上一点，且AE ＝6cm 。

初中数学动点最值问题19⼤模型+例题详解
动点最值问题是中考最难的压轴类题⽬，很多同学都反应不知道该怎么下⼿。

其实这类题⽬的题型有限，总结归纳有19种，希望同学们对每⼀种都能掌握技巧。

1、对称点模型
2、利⽤三⾓形两边差求最值
3、⼿拉⼿全等取最值
4、⼿拉⼿相似取最值
5、平移构造平⾏四边形求最⼩
6、两点对称勺⼦型连接两端求最⼩
7、两点对称折线连两端求最⼩
8、时钟模型，中点两定边求最⼩值
9、时钟模型，相似两定边求最⼩值
10、转化构造两定边求最值
11、⾯积转化法求最值
12、相似转化法求最值
13、相似系数化⼀法求最值
14、三⾓函数化⼀求最值
15、轨迹最值
16、三动点的垂直三⾓形
17、旋转最值
18、隐圆最值-定⾓动弦
19、隐圆最值-动⾓定弦。

中考压轴题动点形成的最值问题数学因运动而充满活力，数学因变化而精彩纷呈．动态题是近年来中考的的一个热点问题，以运动的观点探究几何图形的变化规律问题，称之为动态几何问题，随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题，就其运动对象而言，有点动、线动、面动三大类，就其运动形式而言，有轴对称（翻折）、平移、旋转（中心对称、滚动）等，就问题类型而言，有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等．解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况．以动态几何问题为基架而精心设计的考题，可谓璀璨夺目、精彩四射． 动态几何形成的最值问题是动态几何中的基本类型，包括单动点形成的最值问题，双（多）动点形成的最值问题，线动形成的最值问题，面动形成的最值问题．本专题原创编写双（多）形成的最值问题模拟题．在中考压轴题中，双（多）形成的最值问题的重点和难点在于应用数形结合的思想准确地进行分类和选择正确的解题方法．原创模拟预测题1．如图，四边形ABCD 中，∠A=90°，AB=33，AD=3，点M ，N 分别为线段BC ，AB 上的动点（含端点，但点M 不与点B 重合），点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为 ．【答案】3． 【解析】试题分析：∵ED=EM ，MF=FN ，∴EF=12DN ，∴DN 最大时，EF 最大，∵N 与B 重合时DN 最大，此时22AD AB ，∴EF 的最大值为3．故答案为：3．考点：三角形中位线定理；勾股定理；动点型．原创模拟预测题2．如图，在四边形ABCD 中，DC ∥AB ，DA ⊥AB ，AD=4cm ，DC=5cm ，AB=8cm ．如果点P 由B 点出发沿BC 方向向点C 匀速运动，同时点Q 由A 点出发沿AB 方向向点B 匀速运动，它们的速度均为1cm/s ，当P 点到达C 点时，两点同时停止运动，连接PQ ，设运动时间为t s ，解答下列问题：（1）当t 为何值时，P ，Q 两点同时停止运动？（2）设△PQB 的面积为S ，当t 为何值时，S 取得最大值，并求出最大值； （3）当△PQB 为等腰三角形时，求t 的值．【答案】（1）5；（2）当t=4时，S 的最大值是325；（3）t=4011秒或t=4811秒或t=4秒．【解析】（2）由题意知，AQ=BP=t ，∴QB=8﹣t ，作PF ⊥QB 于F ，则△BPF ～△BCE ，∴PF BPCE BC =，即45PF t =，∴PF=45t，∴S=12QB•PF=14(8)25t t ⨯-=221655t t -+=2232(4)55t --+（0＜t≤5），∵25-＜0，∴S 有最大值，当t=4时，S 的最大值是325；（3）∵cos ∠B=35BE FB BC BP ==，∴BF=35t ，∴QF=AB ﹣AQ ﹣BF=885t-，∴22QF PF +2284(8)()55t t -+2184455t t -+①当PQ=PB 时，∵PF ⊥QB ，∴BF=QF ，∴BQ=2BF ，即：3825t t-=⨯，解得t=4011； ②当PQ=BQ 时，即218455t t -+﹣t ，即：211480t t -=，解得：10t =（舍去），24811t =；③当QB=BP ，即8﹣t=t ，解得：t=4．综上所述：当t=4011秒或t=4811秒或t=4秒时，△PQB为等腰三角形．考点：四边形综合题；动点型；二次函数的最值；最值问题；分类讨论；压轴题．原创模拟预测题3．如图，在Rt△ABC中，∠ACB＝900，AC=6，BC=8．动点M从点A 出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动．过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒．（1）当t＝秒时，动点M、N相遇；（2）设△PMN的面积为S，求S与t之间的函数关系式；（3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由．【答案】（1）2.5；（2）S=22275156(0 1.4)4860100(1.4 2.5)386010010(2.5)33t ttt ttt tt⎧--≤≤⎪⎪-+⎪<≤⎨⎪⎪-+-<≤⎪⎩；（3）在整个运动过程中，△KAC的面积会发生变化，最小值为1.68，最大值为4．【解析】（3）分两种情况讨论，①当P 在BC 上运动时，如图4，当P 与C 重合时，ΔKACS 最小，当t=0是，M 与A 重合，N 与B 重合，如图5，此时三角形ΔKACS 最大；②当P 在CA 上运动时，如图6，过K 作KE ⊥AC 于E ，过M 作MF ⊥AC 于F ，可以得到ΔKAC S =65t，而101.43t ≤≤，故当 1.4t =时，ΔKAC S 的最小值=6 1.4 1.685⨯=，当103t =时，ΔKAC S 的最大值=610453⨯=．综合①②可得到结论．试题解析：（1）∵∠ACB ＝900，AC=6，BC=8，∴AB=10，当M 、N 相遇时，有310t t +=，∴ 2.5t =；（2）∵N 比M 运动的速度快，∴P 先在BC 上运动，然后在CA 上运动．当P 与C 重合时，∵ΔABC S=12AC •BC=12AB •GC ，∴GC=6×8÷10=4.8，∴226 4.8-，∴BG=10－3.6=6.4，∵AM=t ，BN=3t ，∴MN=10－4t ，MG=GN=12MN=1(104)2t -=52t -，∴52 3.6t t +-=，∴ 1.4t =．①当0 1.4t≤≤时，M在N的左边，P先在BC上向C靠近，如图1，∵AM=t，BN=3t，∴MN=10－4t，MG=GN=12MN=1(104)2t-=52t-，∴GB=GN+NB=523t t-+=5t+，∵tanB=PG ACGB BC=，∴658PGt=+，∴PG=3(5)4t+，∴S=ΔPMNS=12MN•PG= GN•PG=3(52)(5)4t t-⨯+=2751564t t--；②当1.4 2.5t<≤时，M在N的左边，在AC上逐渐远离C，如图2，由①可知，GN=MG=52t-，AM=t，∴AG=MG+AM=5t-，tanA=PG BCAG AC=，∴856PGt=-，∴PG=4(5)3t-，∴S=ΔPMNS=12MN•PG= GN•PG=4(52)(5)3t t-⨯-=28601003t t-+；③当102.53t<≤时，M在N的右边，在AC上逐渐远离C，如图3．MN=NB+AM－AB=310t t+-=410t-，GN=MG=25t-，AM=t，∴AG= AM－MG =(25)t t--=5t-，tanA=PG BCAG AC=，∴856PGt=-，∴PG=4(5)3t-，∴S=ΔPMNS=12MN •PG= GN•PG=4(25)(5)3t t-⨯-=28601003t t-+-；∴S=22275156(0 1.4)4860100(1.4 2.5)386010010(2.5)33t ttt ttt tt⎧--≤≤⎪⎪-+⎪<≤⎨⎪⎪-+-<≤⎪⎩；②当P在CA上运动时，如图6，过K作KE⊥AC于E，过M作MF⊥AC于F，∴EK∥FM，∵K为PM的中点，∴EK=12FM，∵FM⊥AC，CB⊥AC，∴FM∥CB，∴FM AMBC AB=，∴810FM t=，∴FM=45t，∴EK=12FM=25t，∴ΔKACS=12AC•EK=12625t⨯⨯=65t，∵101.43t≤≤，∴当 1.4t=时，ΔKACS的最小值=61.4 1.685⨯=，当103t=时，ΔKACS的最大值=610453⨯=．∴当P在CA上运动时，△KAC面积的最小值为1.68，最大值为4．综合①②可得：在整个运动过程中，△KAC的面积会发生变化，最小值为1.68，最大值为4．考点：三角形综合题；动点型；分类讨论；最值问题；分段函数；压轴题．原创模拟预测题4．如图，二次函数cxaxy++=22的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3）．（1）求该二次函数的表达式；（2）过点A的直线AD∥BC且交抛物线于另一点D，求直线AD的函数表达式；（3）在（2）的条件下，请解答下列问题：①在x轴上是否存在一点P，使得以B、C、P为顶点的三角形与△ABD 相似？若存在，求出点P 的坐标；若不存在，请说明理由； ②动点M 以每秒1个单位的速度沿线段AD 从点A 向点D 运动，同时，动点N以每秒513个单位的速度沿线段DB 从点D 向点B 运动，问：在运动过程中，当运动时间t 为何值时，△DMN 的面积最大，并求出这个最大值．【答案】（1）322++-=x x y ；（2）1y x =--；（3）①P （35，0）或P （﹣4.5，0）；②当225=t 时，MDN S ∆的最大值为25．【解析】②过点B 作BF ⊥AD 于F ，过点N 作NE ⊥AD 于E ，在Rt △AFB 中，∠BAF=45°，于是可求得BF ，BD 的长，进而求得sin ∠ADB ，由于DM=t -25，DN=t513，于是得到NE DM S MDN ⋅=∆21=t t 52)25(21⋅-=，整理配方即可得到结果． 试题解析：（1）由题意知：023a c c =-+⎧⎨=⎩，解得：13a c =-⎧⎨=⎩，∴二次函数的表达式为322++-=x x y ；（2）在322++-=x x y 中，令y=0，则2230x x -++=，解得：11x =-，23x =，∴B （3，0），由已知条件得直线BC 的解析式为3y x =-+，∵AD ∥BC ，∴设直线AD 的解析式为y x b =-+，∴0=1+b ，∴b=﹣1，∴直线AD 的解析式为1y x =--；（3）①∵BC ∥AD ，∴∠DAB=∠CBA ，∴只要当：AB PB AD BC =或AD PBAB BC =时，△PBC ∽△ABD ，解：2231x y y x x ⎧⎨=-+-=-+⎩，得D （4，﹣5），∴AD=25，AB=4，BC=23，设P 的坐标为（x ，0），即432523x -=或253423x -=，解得53=x 或5.4-=x ，∴P （35，0）或P （﹣4.5，0），②过点B 作BF ⊥AD 于F ，过点N 作NE ⊥AD 于E ， 在Rt △AFB 中，∠BAF=45°，∴AB BFBAF =∠sin ，∴BF=22224=⨯，BD=26，∴131322622sin ===∠BD BF ADB ， ∵DM=t -25，DN=t513，又∵DN NE ADB =∠sin ，NE=t 513t5213132=⋅， ∴NE DM S MDN ⋅=∆21=t t 52)25(21⋅-=)25(5125122t t t t --=+-=25)225(512+--=t ，∴当225=t 时，MDN S ∆的最大值为25．考点：二次函数综合题；分类讨论；相似三角形的判定与性质；最值问题；二次函数的最值；动点型；压轴题．原创模拟预测题5．如图，在矩形纸片ABCD 中，AB=4，AD=12，将矩形纸片折叠，使点C 落在AD 边上的点M 处，折痕为PE ，此时PD=3． （1）求MP 的值；（2）在AB 边上有一个动点F ，且不与点A ，B 重合．当AF 等于多少时，△MEF 的周长最小？（3）若点G ，Q 是AB 边上的两个动点，且不与点A ，B 重合，GQ=2．当四边形MEQG 的周长最小时，求最小周长值．（计算结果保留根号）【答案】（1）5；（2）1611；（3）755+．【解析】 试题分析：（1）由折叠的性质和矩形性质以得PD=PH=3，CD=MH=4，∠H=∠D=90°，利用勾股定理可计算出MP 的长；（2）如图1，作点M 关于AB 的对称点M′，连接M′E 交AB 于点F ，利用两点之间线段最短可得点F 即为所求，过点E 作EN ⊥AD ，垂足为N ，则AM=AD ﹣MP ﹣PD=4，所以AM=AM′=4，再证明ME=MP=5，利用勾股定理计算出MN=3，NM′=11，得出△AFM′∽△NEM′，利用相似比即可计算出AF；（3）如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R 交AB于点G，再过点E作EQ∥RG，交AB于点Q，易得QE=GR，而GM=GM′，于是MG+QE=M′R，利用两点之间线段最短可得此时MG+EQ最小，于是四边形MEQG的周长最小，在Rt△M′RN中，利用勾股定理计算出M′R得出，从而得到四边形MEQG的最小周长值．（3）如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R 交AB于点G，再过点E作EQ∥RG，交AB于点Q，∵ER=GQ，ER∥GQ，∴四边形ERGQ 是平行四边形，∴QE=GR，∵G M=GM′，∴MG+QE=GM′+GR=M′R，此时MG+EQ最小，四边形MEQG的周长最小，在Rt△M′RN中，NR=4﹣2=2，M′R=22112+=55，∵ME=5，GQ=2，∴四边形MEQG的最小周长值是755+．考点：几何变换综合题；动点型；最值问题；翻折变换（折叠问题）；综合题；压轴题．原创模拟预测题6．抛物线213242y x x=-+与x轴交于A，B两点（OA＜OB），与y轴交于点C．（1）求点A，B，C的坐标；（2）点P从点O出发，以每秒2个单位长度的速度向点B运动，同时点E也从点O出发，以每秒1个单位长度的速度向点C运动，设点P的运动时间为t秒（0＜t＜2）．①过点E 作x 轴的平行线，与BC 相交于点D （如图所示），当t 为何值时，11OP ED +的值最小，求出这个最小值并写出此时点E ，P 的坐标；②在满足①的条件下，抛物线的对称轴上是否存在点F ，使△EFP 为直角三角形？若存在，请直接写出点F 的坐标；若不存在，请说明理由．【答案】（1） A （2，0），B （4，0），C （0，2）；（2）①t=1时，11OP ED +有最小值1，此时OP=2，OE=1， E （0，1），P （2，0）；②F （3，2），（3，7）．【解析】 试题分析：（1）在抛物线的解析式中，令y=0，令x=0，解方程即可得到结果； （2）①由题意得：OP=2t ，OE=t ，通过△CDE ∽△CBO 得到CE ED CO OB =，即224t DE -=，求得11OP ED +有最小值1，即可求得结果；②存在，求得抛物线的对称方程为x=3，设F （3，m ），当△EFP 为直角三角形时，①当∠EPF=90°时，②当∠EFP=90°时，③当∠PEF=90°时，根据勾股定理列方程即可求得结果．试题解析：（1）在抛物线的解析式中，令y=0，即2132042x x -+=，解得：12x =，24x =，∵OA ＜OB ，∴A （2，0），B （4，0），在抛物线的解析式中，令x=0，得y=2，∴C （0，2）；（2）①由题意得：OP=2t ，OE=t ，∵DE ∥OB ，∴△CDE ∽△CBO ，∴CE ED CO OB =，即224t DE -=，∴DE=4﹣2t ， ∴11OP ED +=11242t t +-=212t t -+=211(1)t --，∵0＜t ＜2，21(1)t --始终为正数，且t=1时，21(1)t --有最大值1，∴t=1时，211(1)t --有最小值1，即t=1时，11OP ED +有最小值1，此时OP=2，OE=1，∴E （0，1），P （2，0）； ②存在，∵抛物线213242y x x =-+的对称轴方程为x=3，设F （3，m ），∴25EP =，2PF =22(32)m -+，2EF =22(1)3m -+，当△EFP 为直角三角形时，①当∠EPF=90°时，222EPPF EF +=，即22225(32)(1)3m m +-+=-+，解得：m=2， ②当∠EFP=90°时，222EF PF EP +=，即2222(1)3(32)5m m -++-+=，解得；m=0或m=1，不合题意舍去，∴当∠EFP=90°时，这种情况不存在，③当∠PEF=90°时，222EF PE PF +=，即2222(1)35(32)m m -++=-+，解得：m=7， 综上所述，F （3，2），（3，7）．考点：二次函数综合题；动点型；最值问题；二次函数的最值；分类讨论；压轴题．原创模拟预测题7．如图，在△ABC 中，AB=5，AC=9，ΔABC 272S =，动点P 从A 点出发，沿射线AB 方向以每秒5个单位的速度运动，动点Q 从C 点出发，以相同的速度在线段AC 上由C 向A 运动，当Q 点运动到A 点时，P 、Q 两点同时停止运动，以PQ 为边作正方形PQEF （P 、Q 、E 、F 按逆时针排序），以CQ 为边在AC 上方作正方形QCGH ．（1）求tanA 的值；（2）设点P 运动时间为t ，正方形PQEF 的面积为S ，请探究S 是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；（3）当t 为何值时，正方形PQEF 的某个顶点（Q 点除外）落在正方形QCGH 的边上，请直接写出t 的值．【答案】（1）34；（2）8110；（3）t 的值为：914或911或1或97．【解析】试题分析：（1）如图1，过点B 作BM ⊥AC 于点M ，利用面积法求得BM 的长度，利用勾股定理得到AM 的长度，最后由锐角三角函数的定义进行解答；（2）如图2，过点P 作PN ⊥AC 于点N ．利用（1）中的结论和勾股定理得到222PN NQ PQ +=，所以由正方形的面积公式得到S 关于t 的二次函数，利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值；（3）需要分类讨论：当点E在边HG上、点F在边HG上、点P边QH（或点E在QC上）、点F边C上时相对应的t的值．（3）分四种情况讨论：①如图3，当点E在边HG上时，t=9 14；②如图4，当点F在边HG上时，t=9 11；③如图5，当点P边QH（或点E在QC上）时，t=1；④如图6，当点F边C上时，t=9 7；综上所述：t的值为：914或911或1或97．考点：四边形综合题；最值问题；二次函数的最值；分类讨论；动点型；存在型；综合题；压轴题．。

重难点几何动点及最值、存在性问题目录题型01将军饮马问题题型02胡不归问题题型03阿氏圆问题题型04隐圆问题题型05费马点问题题型06瓜豆原理模型题型07等腰(边)三角形存在问题题型08直角三角形存在问题题型09平行四边形存在问题题型10矩形、菱形、正方形存在问题题型11全等/相似存在性问题题型12角度存在性问题【命题趋势】动态几何问题是近年来中考的一个重难点问题，以运动的观点探究几何图形或函数与几何图形的变化规律，从而确定某一图形的存在性问题．随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题．【基本原理】1)基本原理(定点到定点)：两点之间，线段最短.2)三角形两边之和>第三边3)基本原理(定点到定线)：垂线段最短.4)平行线的距离处处相等.5)基本原理(定点到定圆)：点圆之间，点心线截距最短(长).6)基本原理(定线到定圆)：线圆之间，心垂线截距最短.7)基本原理(定圆到定圆)：圆圆之间，连心线截距最短(长).【解题思路】1)动态几何问题是以几何图形为背景的，几何图形有直线型和曲线型两种，那么动态几何也有直线型的和曲线型的两类，即全等三角形、相似三角形中的动态几何问题，也有圆中的动态问题．有点动、线动、面动，就其运动形式而言，有平移、旋转、翻折、滚动等．根据其运动的特点，又可分为(1)动点类(点在线段或弧线上运动)也包括一个动点或两个动点；(2)动直线类；(3)动图形问题．2)解决动态几何题，通过观察，对几何图形运动变化规律的探索，发现其中的“变量”和“定量”动中求静，即在运动变化中探索问题中的不变性；动静互化抓住“静”的瞬间，使一般情形转化为特殊问题，从而找到“动与静”的关系；这需要有极敏锐的观察力和多种情况的分析能力，加以想象、结合推理，得出结论．解决这类问题，要善于探索图形的运动特点和规律抓住变化中图形的性质与特征，化动为静，以静制动．解决运动型试题需要用运动与变化的眼光去观察和研究图形，把握图形运动与变化的全过程，抓住其中的等量关系和变量关系，并特别关注--些不变量和不变关系或特殊关系．3)动态几何形成的存在性问题，重点和难点在于应用分类思想和数形结合的思想准确地进行分类，包括等腰(边)三角形存在问题，直角三角形存在问题，平行四边形存在问题，矩形、菱形、正方形存在问题．全等三角形存在问题，相似三角形存在问题等．题型01 将军饮马问题1(2023·辽宁盘锦·中考真题)如图，四边形ABCD 是矩形，AB =10，AD =42，点P 是边AD 上一点(不与点A ，D 重合)，连接PB ，PC ．点M ，N 分别是PB ，PC 的中点，连接MN ，AM ，DN ，点E 在边AD 上，ME ∥DN ，则AM +ME 的最小值是()A.23B.3C.32D.42【答案】C【分析】根据直线三角形斜边中线的性质可得AM =12BP ，DN =12CP ，通过证明四边形MNDE 是平行四边形，可得ME =DN ，则AM +ME =AM +DN =12BP +CP ，作点C 关于直线AD 的对称点M ，则BP +CP =BP +PM ，点B ，P ，M 三点共线时，BP +PM 的值最小，最小值为BM ．【详解】解：∵四边形ABCD 是矩形，∴∠BAP =∠CDP =90°，AD ∥BC ，∵点M ，N 分别是PB ，PC 的中点，∴AM =12BP ，DN =12CP ，MN =12BC ，MN ∥BC ，∵AD ∥BC ，MN ∥BC ，∴MN ∥BC ，又∵ME ∥DN ，∴四边形MNDE 是平行四边形，∴ME =DN ，∴AM +ME =AM +DN =12BP +CP ，如图，作点C 关于直线AD 的对称点M ，连接PM ，BM ，则BP +CP =BP +PM ，当点B ，P ，M 三点共线时，BP +PM 的值最小，最小值为BM ，在Rt △BCM 中，MC =2CD =2AB =210，BC =AD =42，∴BM =BC 2+MC 2=42 2+210 2=62，∴AM +ME 的最小值=12BM =32，故选C ．【点睛】本题考查矩形的性质，直线三角形斜边中线的性质，中位线的性质，平行四边形的判定与性质，轴对称的性质，勾股定理，线段的最值问题等，解题的关键是牢固掌握上述知识点，熟练运用等量代换思想．2(2023·广东广州·中考真题)如图，正方形ABCD 的边长为4，点E 在边BC 上，且BE =1，F 为对角线BD 上一动点，连接CF ，EF ，则CF +EF 的最小值为．【答案】17【分析】连接AE 交BD 于一点F ，连接CF ，根据正方形的对称性得到此时CF +EF =AE 最小，利用勾股定理求出AE 即可．【详解】解：如图，连接AE 交BD 于一点F ，连接CF ，∵四边形ABCD 是正方形，∴点A 与点C 关于BD 对称，∴AF =CF ，∴CF +EF =AF +EF =AE ，此时CF +EF 最小，∵正方形ABCD 的边长为4，∴AD =4,∠ABC =90°，∵点E 在AB 上，且BE =1，∴AE =AB 2+BE 2=42+12=17，即CF +EF 的最小值为17故答案为：17．【点睛】此题考查正方形的性质，熟练运用勾股定理计算是解题的关键．3(2023·四川宜宾·中考真题)如图，在平面直角坐标系xOy 中，等腰直角三角形ABC 的直角顶点C 3，0 ，顶点A 、B 6，m 恰好落在反比例函数y =k x第一象限的图象上．(1)分别求反比例函数的表达式和直线AB 所对应的一次函数的表达式；(2)在x 轴上是否存在一点P ，使△ABP 周长的值最小．若存在，求出最小值；若不存在，请说明理由．【答案】(1)y =6，y =-1x +4(2)在x 轴上存在一点P 5,0 ，使△ABP 周长的值最小,最小值是25+42．【分析】(1)过点A 作AE ⊥x 轴于点E ，过点B 作BD ⊥x 轴于点D ，证明△ACE ≌△CBD AAS ，则CD =AE =3,BD =EC =m ，由OE =3-m 得到点A 的坐标是3-m ,3 ，由A 、B 6，m 恰好落在反比例函数y =k x第一象限的图象上得到33-m =6m ，解得m =1，得到点A 的坐标是2,3 ，点B 的坐标是6,1 ，进一步用待定系数法即可得到答案；(2)延长AE 至点A ，使得EA =AE ，连接A B 交x 轴于点P ，连接AP ，利用轴对称的性质得到AP =A P ，A2,-3 ，则AP +PB =A B ，由AB =25知AB 是定值，此时△ABP 的周长为AP +PB +AB =AB +A B 最小，利用待定系数法求出直线A B 的解析式，求出点P 的坐标，再求出周长最小值即可．【详解】(1)解：过点A 作AE ⊥x 轴于点E ，过点B 作BD ⊥x 轴于点D ，则∠AEC =∠CDB =90°，∵点C 3，0 ，B 6，m ，∴OC =3,OD =6, BD =m ，∴CD =OD -OC =3，∵△ABC 是等腰直角三角形，∴∠ACB =90°,AC =BC ，∵∠ACE +∠BCD =∠CBD +∠BCD =90°，∴∠ACE =∠CBD ，∴△ACE ≌△CBD AAS ，∴CD =AE =3,BD =EC =m ，∴OE =OC -EC =3-m ，∴点A 的坐标是3-m ,3 ，∵A 、B 6，m 恰好落在反比例函数y =k x第一象限的图象上．∴33-m =6m ，解得m =1，∴点A 的坐标是2,3 ，点B 的坐标是6,1 ，∴k =6m =6，∴反比例函数的解析式是y =6x，设直线AB 所对应的一次函数的表达式为y =px +q ，把点A 和点B 的坐标代入得，2p +q =36p +q =1 ，解得p =-12q =4 ,∴直线AB 所对应的一次函数的表达式为y =-12x +4，(2)延长AE 至点A ，使得EA =AE ，连接A B 交x 轴于点P ，连接AP ，∴点A 与点A 关于x 轴对称，∴AP =A P ，A 2,-3，∵AP +PB =A P +PB =A B ，∴AP +PB 的最小值是A B 的长度，∵AB =2-6 2+3-1 2=25，即AB 是定值，∴此时△ABP 的周长为AP +PB +AB =AB +A B 最小，设直线A B 的解析式是y =nx +t ，则2n +t =-3 ，解得n =1t =-5 ，∴直线A B 的解析式是y =x -5，当y =0时，0=x -5，解得x =5，即点P 的坐标是5,0 ，此时AP +PB +AB =AB +A B =25+2-6 2+-3-1 2=25+42，综上可知，在x 轴上存在一点P 5,0 ，使△ABP 周长的值最小，最小值是25+42．【点睛】此题考查了反比例函数和一次函数的图象和性质、用到了待定系数法求函数解析式、勾股定理求两点间距离、轴对称最短路径问题、全等三角形的判定和性质等知识，数形结合和准确计算是解题的关键．题型02 胡不归问题1(2022·内蒙古鄂尔多斯·中考真题)如图，在△ABC 中，AB =AC =4，∠CAB =30°，AD ⊥BC ，垂足为D ，P 为线段AD 上的一动点，连接PB 、PC ．则PA +2PB 的最小值为．【答案】42【分析】在∠BAC 的外部作∠CAE =15°，作BF ⊥AE 于F ，交AD 于P ，此时PA +2PB =212PA +PB=12PF +PB =2BF ，通过解直角三角形ABF ，进一步求得结果．【详解】解：如图，在∠BAC 的外部作∠CAE =15°，作BF ⊥AE 于F ，交AD 于P ，此时PA +2PB 最小，∴∠AFB =90°∵AB =AC ，AD ⊥BC ，∴∠CAD =∠BAD =12∠BAC =12×30°=15°，∴∠EAD =∠CAE +∠CAD =30°，∴PF =12PA ，∴PA +2PB =212PA +PB =12PF +PB =2BF ，在Rt △ABF 中，AB =4，∠BAF =∠BAC +∠CAE =45°，∴BF =AB •sin45°=4×22=22，∴(PA +2PB )最大=2BF =42，故答案为：42．【点睛】本题考查了等腰三角形的性质，解直角直角三角形，解题的关键是作辅助线．2(2023·湖南湘西·中考真题)如图，⊙O 是等边三角形ABC 的外接圆，其半径为4．过点B 作BE ⊥AC 于点E ，点P 为线段BE 上一动点(点P 不与B ，E 重合)，则CP +12BP 的最小值为．【答案】6【分析】过点P 作PD ⊥AB ，连接CO 并延长交AB 于点F ，连接AO ，根据等边三角形的性质和圆内接三角形的性质得到OA =OB =4，CF ⊥AB ，然后利用含30°角直角三角形的性质得到OE =12OA =2，进而求出BE =BO +EO =6，然后利用CP +12BP =CP +PD ≤CF 代入求解即可．【详解】如图所示，过点P 作PD ⊥AB ，连接CO 并延长交AB 于点F ，连接AO∵△ABC 是等边三角形，BE ⊥AC∴∠ABE =∠CBE =12∠ABC =30°∵⊙O 是等边三角形ABC 的外接圆，其半径为4∴OA =OB =4，CF ⊥AB ，∴∠OBA =∠OAB =30°∴∠OAE =∠OAB =12∠BAC =30°∵BE ⊥AC∴OE =12OA =2∴BE =BO +EO =6∵PD ⊥AB ，∠ABE =30°∴PD =12PB ∴CP +12BP =CP +PD ≤CF ∴CP +12BP 的最小值为CF 的长度∵△ABC 是等边三角形，BE ⊥AC ，CF ⊥AB∴CF =BE =6∴CP +12BP 的最小值为6．故答案为：6．【点睛】此题考查了圆内接三角形的性质，等边三角形的性质，含30°角直角三角形的性质等知识，解题的关键是熟练掌握以上知识点．3(2023·辽宁锦州·中考真题)如图，在Rt △ABC 中，∠ACB =90°，∠ABC =30°，AC =4，按下列步骤作图：①在AC 和AB 上分别截取AD 、AE ，使AD =AE ．②分别以点D 和点E 为圆心，以大于12DE 的长为半径作弧，两弧在∠BAC 内交于点M ．③作射线AM 交BC 于点F ．若点P 是线段AF 上的一个动点，连接CP ，则CP +12AP 的最小值是．【答案】23【分析】过点P 作PQ ⊥AB 于点Q ，过点C 作CH ⊥AB 于点H ，先利用角平分线和三角形的内角和定理求出∠BAF =30°，然后利用含30°的直角三角的性质得出PQ =12AP ，则CP +12AP =CP +PQ ≥CH ，当C 、P 、Q 三点共线，且与AB 垂直时，CP +12AP 最小，CP +12AP 最小值为CH ，利用含30°的直角三角的性质和勾股定理求出AB ，BC ，最后利用等面积法求解即可．【详解】解：过点P 作PQ ⊥AB 于点Q ，过点C 作CH ⊥AB 于点H ，由题意知：AF 平分∠BAC ，∵∠ACB =90°，∠ABC =30°，∴∠BAC =60°，∴∠BAF =12∠BAC =30°，∴PQ =12AP ，∴CP +12AP =CP +PQ ≥CH ，∴当C 、P 、Q 三点共线，且与AB 垂直时，CP +12AP 最小，CP +12AP 最小值为CH ，∵∠ACB =90°，∠ABC =30°，AC =4，∴AB =2AC =8，∴BC =AB 2-AC 2=43，∵S △ABC =12AC ⋅BC =12AB ⋅CH ，∴CH =AC ⋅BC AB =4×438=23，即CP +12AP 最小值为23．故答案为：23．【点睛】本题考查了尺规作图-作角平分线，含30°的直角三角形的性质，勾股定理等知识，注意掌握利用等积法求三角形的高或点的线的距离的方法．题型03 阿氏圆问题1(2023·山东烟台·中考真题)如图，抛物线y =ax 2+bx +5与x 轴交于A ,B 两点，与y 轴交于点C ,AB =4．抛物线的对称轴x =3与经过点A 的直线y =kx -1交于点D ，与x 轴交于点E ．(1)求直线AD 及抛物线的表达式；(2)在抛物线上是否存在点M ，使得△ADM 是以AD 为直角边的直角三角形?若存在，求出所有点M 的坐标；若不存在，请说明理由；(3)以点B 为圆心，画半径为2的圆，点P 为⊙B 上一个动点，请求出PC +12PA 的最小值．【答案】(1)直线AD 的解析式为y =x -1；抛物线解析式为y =x 2-6x +5(2)存在，点M 的坐标为4,-3 或0,5 或5,0(3)41【分析】(1)根据对称轴x =3，AB =4，得到点A 及B 的坐标，再利用待定系数法求解析式即可；(2)先求出点D 的坐标，再分两种情况：①当∠DAM =90°时，求出直线AM 的解析式为y =-x +1，解方程组y =-x +1y =x 2-6x +5 ，即可得到点M 的坐标；②当∠ADM =90°时，求出直线DM 的解析式为y =-x +5，解方程组y =-x +5y =x 2-6x +5 ，即可得到点M 的坐标；(3)在AB 上取点F ，使BF =1，连接CF ，证得BF PB =PB AB ，又∠PBF =∠ABP ，得到△PBF ∽△ABP ，推出PF =12PA ，进而得到当点C 、P 、F 三点共线时，PC +12PA 的值最小，即为线段CF 的长，利用勾股定理求出CF 即可．【详解】(1)解：∵抛物线的对称轴x =3，AB =4，∴A 1,0 ,B 5,0 ，将A 1,0 代入直线y =kx -1，得k -1=0，解得k =1，∴直线AD 的解析式为y =x -1；将A 1,0 ,B 5,0 代入y =ax 2+bx +5，得a +b +5=025a +5b +5=0 ，解得a =1b =-6 ，∴抛物线的解析式为y =x 2-6x +5；(2)存在点M ，∵直线AD 的解析式为y =x -1，抛物线对称轴x =3与x 轴交于点E ．∴当x =3时，y =x -1=2，∴D 3,2 ，①当∠DAM =90°时，设直线AM 的解析式为y =-x +c ，将点A 坐标代入，得-1+c =0，解得c =1，∴直线AM 的解析式为y =-x +1，解方程组y =-x +1y =x 2-6x +5 ，得x =1y =0 或x =4y =-3 ，∴点M 的坐标为4,-3 ；②当∠ADM =90°时，设直线DM 的解析式为y =-x +d ，将D 3,2 代入，得-3+d =2，解得d =5，∴直线DM 的解析式为y =-x +5，解方程组y =-x +5y =x 2-6x +5 ，解得x =0y =5 或x =5y =0 ，∴点M 的坐标为0,5 或5,0综上，点M 的坐标为4,-3 或0,5 或5,0 ；(3)如图，在AB 上取点F ，使BF =1，连接CF ，∵PB =2，∴BF PB =12，∵PB AB =24=12，、∴BF PB =PB AB，又∵∠PBF =∠ABP ，∴△PBF ∽△ABP ，∴PF PA =BF PB =12，即PF =12PA ，∴PC +12PA =PC +PF ≥CF ，∴当点C 、P 、F 三点共线时，PC +12PA 的值最小，即为线段CF 的长，∵OC =5,OF =OB -1=5-1=4，∴CF =OC 2+OF 2=52+42=41，∴PC +12PA 的最小值为41．【点睛】此题是一次函数，二次函数及圆的综合题，掌握待定系数法求函数解析式，直角三角形的性质，勾股定理，相似三角形的判定和性质，求两图象的交点坐标，正确掌握各知识点是解题的关键．2(2023·山东济南·一模)抛物线y =-12x 2+a -1 x +2a 与x 轴交于A b ,0 ，B 4,0 两点，与y 轴交于点C 0,c ，点P 是抛物线在第一象限内的一个动点，且在对称轴右侧．(1)求a ，b ，c 的值；(2)如图1，连接BC 、AP ，交点为M ，连接PB ，若S △PMB S △AMB=14，求点P 的坐标；(3)如图2，在(2)的条件下，过点P 作x 轴的垂线交x 轴于点E ，将线段OE 绕点O 逆时针旋转得到OE '，旋转角为α(0°<α<90°)，连接E 'B ，E C ，求E B +34E C 的最小值．【答案】(1)a =2，b =-2，c =4(2)P 3,52(3)3374【分析】(1)利用待定系数法求解即可；(2)过点P 作PD ⊥x 轴，交BC 于点D ，过点A 作y 轴的平行线交BC 的延长线于H ，求得l BC 的解析式，设P m ,-12m 2+m +4 ，则D m ,-m +4 ，利用相似三角形的判定与性质可得答案；(3)在y 轴上取一点F ，使得OF =94，连接BF ，由相似三角形的判定与性质可得FE =34CE ，可得E B +34E C =BE +E F ，即可解答．【详解】(1)解：将B 4,0 代入y =-12x 2+a -1 x +2a ，得-8+4a -1 +2a =0，∴a =2，∴抛物线的解析式为y =-12x 2+x +4，令x =0，则y =4，∴c =4，令y =0，则0=-12x 2+x +4，∴x 1=4，x 2=-2，∴A -2,0 ，即b =-2；∴a =2，b =-2，c =4(2)过点P 作PD ⊥x 轴，交BC 于点D ，过点A 作y 轴的平行线交BC 的延长线于H ，设l BC ：y =kx +b ，将0,4 ，4,0 代入得b =44k +b =0 解得：b =4，k =-1，∴l BC ：y =-x +4，设P m ,-12m 2+m +4 ，则D m ,-m +4 ，PD =y P -y D =-12m 2+m +4--m +4 =-12m 2+2m ，∵PD ∥HA ，∴△AMH ∽△PMD ，∴PM MA =PD HA，将x =-2代入y =-x +4，∴HA =6，∵S △PMB S △AMB =12PM ⋅h 12AM ⋅h =PM AM =14，∴PD HA =PD 6=14，∴PD =32，∴32=-12m 2+2m ，∴m 1=1(舍)，m 2=3，∴P 3,52 ；(3)在y 轴上取一点F ，使得OF =94，连接BF ，根据旋转得性质得出：OE =OE =3，∵OF ⋅OC =94×4=9，∴OE 2=OF ⋅OC ，∴OE OF =OC OE，∵∠COE =∠FOE ，∴△FOE ∽△E OC ，∴FE CE =OE OC =34，∴FE =34CE ，∴E B +34E C =BE +E F ，当B 、E '、F 三点共线时，此时E B +34E C 最小=BF ，最小值为：BF =42+94 2=3374．【点睛】此题考查的是二次函数的综合题意，涉及到相似三角形的判定与性质、二次函数与面积的问题、待定系数法求解析式，旋转的性质等知识．正确的作出辅助线是解此题的关键．题型04 隐圆问题1(2022·山东泰安·中考真题)如图，四边形ABCD 为矩形，AB =3，BC =4．点P 是线段BC 上一动点，点M 为线段AP 上一点．∠ADM =∠BAP ，则BM 的最小值为()A.5B.12C.13-3D.13-2【答案】D【分析】证明∠AMD=90°，得出点M在O点为圆心，以AO为半径的圆上，从而计算出答案．【详解】设AD的中点为O，以O点为圆心，AO为半径画圆∵四边形ABCD为矩形∴∠BAP+∠MAD=90°∵∠ADM=∠BAP∴∠MAD+∠ADM=90°∴∠AMD=90°∴点M在O点为圆心，以AO为半径的圆上连接OB交圆O与点N∵点B为圆O外一点∴当直线BM过圆心O时，BM最短∵BO2=AB2+AO2，AO=12AD=2∴BO2=9+4=13∴BO=13∵BN=BO-AO=13-2故选：D．【点睛】本题考查直角三角形、圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．2(2022·安徽蚌埠·一模)如图，Rt△ABC中，AB⊥BC，AB=8，BC=6，P是△ABC内部的一个动点，满足∠PAB=∠PBC，则线段CP长的最小值为()A.325B.2C.213-6D.213-4【答案】D【分析】结合题意推导得∠APB=90°，取AB的中点O，以点O为圆心，AB为直径作圆，连接OP；根据直角三角形斜边中线的性质，得OP=OA=OB=12AB=4；根据圆的对称性，得点P在以AB为直径的⊙O上，根据两点之间直线段最短的性质，得当点O、点P、点C三点共线时，PC最小；根据勾股定理的性质计算得OC，通过线段和差计算即可得到答案．【详解】∵∠ABC=90°，∴∠ABP+∠PBC=90°，∵∠PAB=∠PBC，∴∠BAP+∠ABP=90°，∴∠APB=90°，取AB的中点O，以点O为圆心，AB为直径作圆，连接OP，∴OP=OA=OB=12AB=4∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，当点O、点P、点C三点共线时，PC最小在Rt△BCO中，∵∠OBC=90°，BC=6，OB=4，∴OC=BO2+BC2=42+62=213，∴PC=OC-OP=213-4∴PC最小值为213-4故选：D．【点睛】本题考查了两点之间直线段最短、圆、勾股定理、直角三角形斜边中线的知识；解题的关键是熟练掌握圆的对称性、两点之间直线段最短、直角三角形斜边中线的性质，从而完成求解．3(20-21九年级上·江苏盐城·期末)如图，⊙M的半径为4，圆心M的坐标为(5,12)，点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为．【答案】18【分析】由RtΔAPB中AB=2OP知要使AB取得最小值，则PO需取得最小值，连接OM，交⊙M于点P'，当点P位于P'位置时，OP'取得最小值，据此求解可得．【详解】解：连接OP，∵PA⊥PB，∴∠APB=90°，∵AO=BO，∴AB=2PO，若要使AB取得最小值，则PO需取得最小值，连接OM，交⊙M于点P'，当点P位于P'位置时，OP'取得最小值，过点M作MQ⊥x轴于点Q，则OQ=5，MQ=12，∴OM=13，又∵MP'=4，∴OP'=9，∴AB=2OP'=18，故答案是：18．【点睛】本题主要考查点与圆的位置关系，解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置．4(2021九年级·全国·专题练习)如图，在平面直角坐标系xOy中，点A与点B的坐标分别是(1，0)，(7，0)．(1)对于坐标平面内的一点P，给出如下定义：如果∠APB=45°，则称点P为线段AB的“等角点”．显然，线段AB的“等角点”有无数个，且A、B、P三点共圆．①设A 、B 、P 三点所在圆的圆心为C ，直接写出点C 的坐标和⊙C 的半径；②y 轴正半轴上是否有线段AB 的“等角点”？如果有，求出“等角点”的坐标；如果没有，请说明理由；(2)当点P 在y 轴正半轴上运动时，∠APB 是否有最大值？如果有，说明此时∠APB 最大的理由，并求出点P 的坐标；如果没有请说明理由．【答案】(1)①(4，3)或(4,-3)，半径为32；②存在，(0，3+2)或(0，3-2)，见解析；(2)有，见解析，(0，7)【分析】(1)①在x 轴的上方，作以AB 为斜边的等腰直角三角形△ACB ，易知A ，B ，P 三点在⊙C 上，圆心C 的坐标为(4,3)，半径为32，根据对称性可知点C (4，-3)也满足条件；②当圆心为C (4，3)时，过点C 作CD ⊥y 轴于D ，则D (0，3)，CD =4，根据⊙C 的半径得⊙C 与y 轴相交，设交点为P 1，P 2，此时P 1，P 2在y 轴的正半轴上，连接CP 1、CP 2、CA ，则CP 1=CP 2=CA =r =32，得DP 2=2，即可得；(2)如果点P 在y 轴的正半轴上，设此时圆心为E ，则E 在第一象限，在y 轴的正半轴上任取一点M (不与点P 重合)，连接MA ，MB ，PA ，PB ，设MB 交于⊙E 于点N ，连接NA ，则∠APB =∠ANB ，∠ANB 是△MAN的外角，∠ANB >∠AMB ，即∠APB >∠AMB ，过点E 作EF ⊥x 轴于F ，连接EA ，EP ，则AF =12AB =3，OF =4，四边形OPEF 是矩形，OP =EF ，PE =OF =4，得EF =7，则OP =7，即可得．【详解】(1)①如图1中，在x 轴的上方，作以AB 为斜边的等腰直角三角形△ACB ，易知A ，B ，P 三点在⊙C 上，圆心C 的坐标为(4,3)，半径为32，根据对称性可知点C (4,-3)也满足条件；②y 轴的正半轴上存在线段AB 的“等角点“。

2023年安徽中考物理总复习专题：最值问题类型一单动点求两线段和的最小值将军饮马问题：两点在一直线同侧时，作一个点的对称点与另一个点连接，所得线段的长即为所求。

典例1如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，点P是边BC上一动点，点D在边AB上，且BD=14AB，则PA+PD的最小值为（ ）A．8B．43C．213D．833【思路】作D关于BC的对称点E，连接AE交BC于P，则PA+PD的值最小，过E作EF⊥AC交AC的延长线于F，过D作DH⊥AC于H，则DH＝EF，DH∥BC，根据勾股定理即可得到结论．解：作D关于BC的对称点E，连接AE交BC于P，则PA+PD的值最小，过E作EF⊥AC 交AC的延长线于F，过D作DH⊥AC于H，则DH＝EF，DH∥BC，∵∠ACB＝90°，∠B＝30°，AB＝8，∴AC=12AB＝4，∠ADH＝∠B＝30°，∵BD=14AB＝2，∴AD＝6，CF=12DE=12BD＝1，∴AF＝5，∴DH=AD2―AH2=33，∴EF＝33，∴AE=AF2+EF2=213，∴PA+PD的最小值为213．【总结】本题考查了轴对称﹣最短路线问题，含30°角的直角三角形的性质，勾股定理，正确的作出辅助线是解题的关键．针对训练1如图，在△ABC中，AB＝AC，AD，BE是△ABC的两条中线，AD＝5，BE＝6，P是AD上的一个动点，连接PE，PC，则PC+PE的最小值是（ ）A．5B．6C．7D．8类型二求一条线段的最小值垂线段最短典例2如图，OP平分∠AOB，PD⊥OA于点D，点E是射线OB上的一个动点，若PD＝3，则PE的最小值是　．【思路】过P作PE⊥OB于E，根据垂线段最短得出此时PE的长最小，根据角平分线的性质得出PE＝PD，再求出答案即可．解：过P作PE⊥OB于E，此时PE的长最小，∵OP平分∠AOB，PD⊥OA，PE⊥OB，∴PE＝PD，∵PD＝3，∴PE＝3，即PE的最小值是3．【总结】本题考查了垂线段最短和角平分线的性质，能找出当PE最小时点E的位置是解此题的关键．针对训练2如图，在△ABC中，∠C＝90°，BD为△ABC的角平分线，过点D作直线l∥AB，点P为直线l上的一个动点，若△BCD的面积为16，BC＝8，则AP最小值为 ．类型三双动点求两线段和的最小值将军饮马问题与垂线段最短的综合典例2如图，在Rt△ABC中，∠ABC＝90°，AB＝6，∠BAC＝30°，∠BAC的平分线交BC 于点D，E，F分别是线段AD和AB上的动点，则BE+EF的最小值是 ．【思路】根据对称性，过点F作FG⊥AC交AD于点Q，连接BG交AD于点E，此时BG＝BE+EF，当BG垂直于AC30°直角三角形的边的性质即可求解．解：方法一：如图1所示：在AC边上截取AB′＝AB，作B′F⊥AB于点F，交AD于点E，∵AD平分∠BAC，∴∠BAE＝∠B′AE，AE＝AE，∴△ABE≌△AB′E（SAS）．∴BE＝B′E，∴B′F＝B′E+EF＝BE+EF，∵垂线段最短，∴此时BE+EF最短．∵AB＝AB′＝6，∠BAC＝30°，∴B′F=12AB′＝3．方法二：如图2所示：在AC边上截取AG＝AF，连接BG交AD于点E，作BH⊥AC于点H，同方法一：得△AEG≌△AFG（SAS）∴EG＝EF，∴BG＝BE+EG＝BE+EF，当BG垂直于AC时最短，即BH的长最短，∵AB＝6，∠BAC＝30°，∴BH＝3．【总结】本题考查了最短路线问题、角分线的性质、含30度角的直角三角形，解决本题的关键是作对称点．针对训练3 已知，等腰△ABC中，AB＝AC，E是高AD上任一点，F是腰AB上任一点，腰AC＝5，BD＝3，AD＝4，那么线段BE+EF的最小值是（ ）A．5B．3C．245D．72针对训练4 在四边形ABCD中，∠ABC＝60°，∠BCD＝45°，BC＝23+2，BD平分∠ABC，若P，Q分别是BD，BC上的动点，则CP+PQ的最小值是（ ）A．23+2B．3+3C．22+2D．2+4类型四一点两线求周长最小值根据轴对称的性质，结合三角形三边关系定理典例4 如图，∠AOB＝30°，∠AOB内有一定点P，且OP＝15，若在OA、OB上分别有动点M、N，则△PMN周长的最小值是（ ）A．5B．15C．20D．30【思路】根据题意画出符合条件的图形，求出OD＝OE＝OP，∠DOE＝60°，得出等边三角形DOE，求出DE＝15，求出△PMN的周长＝DE，即可求出答案．解：作P关于OA的对称点D，作P关于OB的对称点E，连接DE交OA于M，交OB 于N，连接PM，PN，则此时△PMN的周长最小，连接OD，OE，∵P、D关于OA对称，∴OD＝OP，PM＝DM，同理OE＝OP，PN＝EN，∴OD＝OE＝OP＝15，∵P、D关于OA对称，∴OA⊥PD，∵OD＝OP，∴∠DOA＝∠POA，同理∠POB＝∠EOB，∴∠DOE＝2∠AOB＝2×30°＝60°，∵OD＝OE＝15，∴△DOE是等边三角形，∴DE＝15，即△PMN的周长是PM+MN+PN＝DM+MN+EN＝DE＝15．【总结】本题考查了轴对称﹣最短路线问题，关键是画出符合条件的图形，题目具有一定的代表性，是一道比较好的题目．针对训练5 如图，在四边形ABCD中，∠B＝∠D＝90°，∠BAD＝140°，点E，F分别为BC和CD上的动点，连接AE，AF．当△AEF的周长最小时，∠EAF的度数为（ ）A．60°B．90°C．100°D．120°类型五求两条线段差的最大值两点在一直线两侧时，作一个点的对称点，再将对称点与另一点连接所得线段的长。

二次函数最值问题二次函数的最值问题分两类：1 代数类：利润最大问题2 几何类：面积最小问题一利润最大问题某商店将每件进价为8元的某种商品按每件10元出售，一天可销出约100件．该店想通过降低售价、增加销售量的办法来提高利润，经过市场调查，发现这种商品单价每降低0.1元，其销售量可增加10件。

将这种商品的售价降低多少时，能使销售利润最大?在这个问题中，可提出如下问题供学生思考并回答：1．商品的利润与售价、进价以及销售量之间有什么关系?[利润=(售价－进价)×销售量]2．如果不降低售价，该商品每件利润是多少元?一天总的利润是多少元?[10－8=2(元)，(10－8)×100=200(元)]3．若每件商品降价x元，则每件商品的利润是多少元?一天可销售约多少件商品?[(10－8－x)；(100＋100x)]4．x的值是否可以任意取?如果不能任意取，请求出它的范围，[x的值不能任意取，其范围是0≤x≤2]5．若设该商品每天的利润为y元，求y与x的函数关系式。

[y=(10－8－x) (100＋100x)(0≤x≤2)]y=－100x2＋100x＋20D (0≤x≤2)求最大值的两种方法：1》顶点法2》公式法16．某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w＝－2x＋240．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：（1）当x取何值时，y的值最大？（2）如果物价部门规定这种绿茶的销售单价不得高于90元/千克，公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？16解：1 y＝(x－50)∙ w＝(x－50) ∙ (－2x＋240)＝－2x2＋340x－12000，＝－2 (x－85) 2＋2450，∴当x＝85时，y的值最大．2 当y＝2250时，可得方程－2 (x－85 )2 ＋2450＝2250．解这个方程，得x1＝75，x2＝95．根据题意，x2＝95不合题意应舍去．∴当销售单价为75元时，可获得销售利润2250元．练习1 水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克. 经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克. （1）现该商场要保证每天盈利6000元，同时又要顾客得到实惠，那么每千克应涨价多少元？ （2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？2 商场销售一批衬衫，每天可售出 20 件，每件盈利 40 元，为了扩大销售，减少库存，决定采取适当的降价措施，经调查发现，如果一件衬衫每降价 1 元，每天可多售出 2 件。

中考数学典型试题及解析双动点、最值一、动点专练例1如图，已知△ABC是边长为6cm的等边三角形，动点P，Q同时从A、B两点出发，分别沿AB，BC方向匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t(s)，解答下列问题：(1)若△BPQ为直角三角形，求t；(2)设△BPQ的面积为S(cm²)，求S与t的函数关系式；(3)作QR∥BA交AC于点R，连结PR，若△APR∽△PRQ，求t？分析：(1)分两种情况考虑：∠B PQ＝90°，或∠BQP＝90°，由于∠B＝60°，则第三角必为30°，利用30度角所对直角边是斜边的一半，可知BP长是BQ长的两倍或一半，建立方程求解．(2)由于∠B＝60°是特殊角，故不能选PQ为底，过点A作高！可选BP为底，过Q作垂线段QE，则高QE的长也可用含t的代数式表示，S与t的函数关系式也可求；(3)由QR∥BA，可证得△CRQ∽△CAB，△CRQ也为等边三角形，求出QR和PE的长，则QR＝PE，可证四边形EPRQ是矩形，由△APR∽△PRQ，可得出∠QPR＝∠A＝60°，在△PQR中，利用60°，得到PR，QR的比值，列出方程即可求t．解答：例2分析：由翻折知，四边形QPCP′必为筝形，要想使其为菱形，则首先必须是平行四边形，对角线必然互相平分，利用这一点，想到连接PP′，交CQ于点O，则QO＝CO，想办法用含t的代数式表示出CO和QO，问题迎刃而解．解答：二、最值分类(1)垂线段最短型及变式例1：如图，△ABC是以AB为斜边的直角三角形，AC＝4，BC＝3，P为AB上一动点，且PE⊥AC于E，PF⊥BC于F，则线段EF长度的最小值是_______．分析：由PE⊥AC，PF⊥BC，得∠PEC＝∠PFC＝∠C＝90°，可证四边形ECFP 是矩形，想到对角线相等，可连接CP，问题转化为CP的最小值，则CP⊥AB 时，可取最小值．解答：变式：如图，在△ABC中，AB＝3，AC＝4，BC＝5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为________．分析：本题与例1十分类似，先用勾股定理逆定理，证∠BAC＝90°，从而可证四边形AEPF是矩形，M为对角线EF的中点，放在Rt△AEF中，AM长是斜边EF长的一半，连接AP，AP＝EF，则AM也是AP的一半，求出AP 的最小值，AM的最小值就是其一半．解答：(2)将军饮马型及变式例2如图，在矩形ABCD中，AB＝10，BC＝5．若点M、N分别是线段AC，AB上的两个动点，则BM＋MN的最小值为________分析：本题是一个典型的将军饮马问题，属于一定两动型，点B是定点，M，N 是动点，方法大家应该很熟了，作点B关于AC的对称点E，当E，M，N 三点共线，且EN⊥AB时，BM＋MN＝EN最短，而要求这个最小值，则需要利用勾股定理，或者相似解决．解答：作点B关于AC的对称点E，过E作EF⊥AB交于点F，连接BE变式1：分析：显然，这是一个将军饮马问题，但是，P、Q、R三个点均不是定点，不能过定点作对称，那只能选择Q或P作对称．由于原三角形是等边三角形，那么翻折后，可以将等边三角形补成一个菱形，此后思路与例1一致．同时，本题还要求等边三角形的边长，掌握公式就很快！解答：变式2：如图，矩形ABCD中，AB＝2，AD＝1，E为CD中点，P为AB边上一动点(含端点)，F为CP中点，则△CEF的周长最小值为________分析：解答：EDCBACDMNBA练习反馈1. 如图，在△ABC 中，AC=BC=2，∠ACB-90°，D 是BC 边的中点，E 是AB 边 上一动点，则EC+ED 的最小值是 。

中考数学专题复习最值问题（将军饮马）练习一、选择题：1．如图，正方形ABCD的边长是4，点E是DC上一个点，且DE＝1，P点在AC 上移动，则PE＋PD的最小值是（）A．4 B．4.5 C．5.5 D．52．已知线段AB及直线l，在直线l上确定一点P，使PA PB+最小，则下图中哪一种作图方法满足条件（）．A．B．C．D．3．如图1，在菱形ABCD中，AB＝6，∠BAD＝120°，点E是BC边上的一动点，点P是对角线BD上一动点，设PD的长度为x，PE与PC的长度和为y，图2是y 关于x的函数图象，其中H（a，b）是图象上的最低点，则a+b的值为（）A．73B．33C．83D．3 64．如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE＝2，则EM＋CM的最小值为（）A 26B ．3C ．7D ．25．如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8，点F 在边AC 上，并且CF ＝2，点E 为边BC 上的动点，将△CEF 沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是（ ）A ．1.5B ．1.2C ．2.4D ．以上都不对6．如图所示，已知A （1，y 1），B （2，y 2）为反比例函数y 2=x 图象上的两点，动点P （x ，0）在x 轴正半轴上运动，当线段AP 与线段BP 之差达到最大值时，点P 的坐标是（ ）A ．（3，0）B ．（72，0） C ．（53，0） D ．（52，0）7．如图，矩形ABCD 中，46AB BC ==，，点P 是矩形ABCD 内一动点，且12PAB PCD S S ∆∆=，则PC PD +的最小值是（ ）A ．43B ．5C ．213D ．298．如图，⊙M 的半径为2，圆心M 的坐标为（3，4），点P 是⊙M 上的任意一点，PA ⊥PB ，且PA 、PB 与x 轴分别交于A 、B 两点，若点A 、点B 关于原点O 对称，则AB 的最小值为（ ）A ．3B ．4C ．5D ．6二、填空题9．如图所示，在ABC 中，AB AC =，直线EF 是AB 的垂直平分线，D 是BC 的中点，M 是EF 上一个动点，ABC 的面积为12，4BC =，则BDM ∆周长的最小值是_______________．10．如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，6AD=，点F是线段AD上的动点，则BF EF+的最小值为______．11．如图，在矩形ABCD中，AB＝10，BC＝5．若点M、N分别是线段AC，AB上的两个动点，当BM＋MN取最小值时△BMN的周长为______．12．如图，在四边形ABCD中，∠BCD＝50°，∠B＝∠D＝90°，在BC、CD上分别取一点M、N，使△AMN的周长最小，则∠MAN＝_____°．13．如图，在Rt△AOB中，OA＝OB＝2，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线长PQ的最小值为___．14．如图，在直角坐标系中，点A（2，2），C（4，4）是第一象限角平分线上的两点，点B的纵坐标为2，且BA＝CB，在y轴上取一点D，连接AB，BC，AD，CD，使得四边形ABCD的周长最小，则这个周长的最小值为____．15．如图，在Rt ABC中，90AC BC==，点D在BC边上，且1∠=︒，4ACBCD=，点P是AB上一动点，连接PC、PD，则PC PD+的最小值为______．16．如图，P是AOB∠内一定点，点M，N分别在边OA，OB上运动，若30∠=︒，AOBOP=，则PMN的周长的最小值为___________.3三、解答题17．如图，方格图中每个小正方形的边长为1，点A，B，C都是格点．（1）画出△ABC关于直线MN对称的111△．A B CAA的长度．．（2）若B为坐标原点，请写出1A、1B、1C的坐标，并直接写出1（3）如图2，A，C是直线同侧固定的点，D是直线MN上的一个动点，在直线MN 上画出点D，使AD DC+最小．（保留作图痕迹）18．如图，在△ABC中，AB＝AC，AD是△ABC底边BC上的中线，点P为线段AB 上一点．（1）在AD上找一点E，使得PE+EB的值最小；（2）若点P为AB的中点，当∠BPE满足什么条件时，△ABC是等边三角形，并说明理由．19．在平面直角坐标系中，矩形纸片AOBC 按如图方法放置，点A 、B 分别在y 轴和x 轴上，已知OA =2，OB =4，点D 在边AC 上，且AD =1．解答下列问题．（1）点C 的坐标为 _______；（2）在x 轴上有一点E ，使得△CDE 的周长最短，求出点E 的坐标及直线CE 的解析式．（3）在平面直角坐标系内是否存在点P ，使得以C 、D 、P 、E 为顶点的四边形是平行四边形？若存在，求出点P 的坐标；若不存在，说明理由．20．问题提出（1）在图1中作出点B 关于直线AC 的对称点'B问题探究（2）如图2，在ABC 中，6AB AC ==，120BAC ∠=︒，D 为AC 的中点，P 为线段BC 上一点，求AP DP +的最小值.问题解决（3）如图3，四边形ABCD 为小区绿化区，DA DC =，90ADC ∠=︒，663AB =+12BC =，30B ∠=︒，AC 是以D 为圆心，DA 为半径的圆弧.现在规划在AC ，边BC 和边AC 上分别取一点P ，E ，F ，使得DP PE EF PF +++为这一区域小路，求小路长度的最小值.21．如图，在矩形ABCD 中，2AD =，4AB =，AC 为对角线，E 、F 分别为边AB ，CD 上的动点，且EF AC ⊥于点M ，连接AF ，CE ，求AF CE +的最小值．22．如图，正方形ABCD 的边长为4，E 、F 为对角线BD 上的动点，且2EF 连接CE 、CF ，求CEF △周长的最小值．23．如图，在矩形ABCD 中，4AB =，6AD =，点E 、F 分别是AD 、 AB 上的点，且,AE AB =2AF =，若P 、Q 分别是BC 、CD 边上的动点，求四边形EFPQ 周长的最小值．24．在锐角△ABC 中，AB=4，BC=5，∠ACB=45°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数；（2）如图2，连接AA 1，CC 1．若△ABA 1的面积为4，求△CBC 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转过程中，点P 的对应点是点P 1，求线段EP 1长度的最大值与最小值．25．已知Rt△ABC 中∠C ＝Rt ∠，且BC ＝9，∠B ＝30°．（1）如图1、2，若点D 是CB 上一点，且CD ＝3，点E 是AB 上的动点，将△DBE 沿DE 对折，点B 的对应点为B ′（点B ′和点C 在直线AB 的异侧），DB ′与AB 交于点H ．①当∠B ′EA ＝20°时，求∠EDB 的度数．②当△B ′HE 是等腰三角形时，求∠DEB 的度数．（2）如图2，若点D 是CB 上一点，且CD ＝3，M 是线段AC 上的动点，以∠MDN 为直角构造等腰直角△DMN （D ，M ，N 三点顺时针方向排列），在点M 的运动过程中，直接写出CN +NB 的最小值．。