苏教版数学高一-【苏州市高二文科复习参考资料】学案练习7__函数的单调性

高一数学 第2章第7课时 函数的单调性2配套练习 苏教版必修1分层训练1．函数)(x f 在),(b a 和),(d c 都是增函数，若),(),,(21d c x b a x ∈∈，且21x x <那么（ ）A ．)()(21x f x f <B ．)()(21x f x f >C ．)()(21x f x f =D ．无法确定2．已知)(x f 在实数集上是减函数，若0≤+b a ，则下列正确的是 （ ）A ．)]()([)()(b f a f b f a f +-≤+B ． )()()()(b f a f b f a f -+-≤+C ．)]()([)()(b f a f b f a f +-≥+D ．)()()()(b f a f b f a f -+-≥+3．函数y =在区间(,)-∞+∞上是（ ）A ．增函数B ．既不是增函数又不是减函数C ．减函数D ．既是增函数又是减函数考试热点4．如果函数f(x)＝x 2＋2(a －1)x ＋2在区间(,4]-∞上是减函数，那么实数a 的取值范围是（ ）A ．a ≥－3B ．a ≤－3C ．a ≤5D ．a ≥35．函数267([1,7])y x x x =-+∈-的值域 。

6．若函数f(x)=(-k 2+3k+4)x+2是增函数，则k 的范围是7．已知]3,1[,)2()(2-∈-=x x x f ，求函数)1(+x f 得单调递减区间.8．讨论函数)(x f =12-x ax (-1<x <1)的单调性.拓展延伸9．已知函数1)(2+=x x f ，且)]([)(x f f x g =，)()()(x f x g x G λ-=，试问，是否存在实数λ，使得)(x G 在]1,(--∞上为减函数，并且在)0,1(-上为增函数.10．函数)(),(x g x f 在区间],[b a 上都有意义，且在此区间上①)(x f 为增函数，0)(>x f ；②)(x g 为减函数，0)(<x g .判断)()(x g x f 在],[b a 的单调性，并给出证明.本节学习疑点：学生质疑教师释疑。

函 数 的 单 调 性【教学目的】1． 使学生理解增函数、减函数的概念，掌握判断某些函数增减性的方法； 2． 培养学生利用数学概念进行判断推理的能力和数形结合，辩证思维的能力； 【基本知识】1、 定义：对于给定区间上的函数f(x)及属于这个区间上的任意两个自变量x 1、x 2，当x 1＜x 2时，如果有f(x 1)＜f(x 2)，则称f(x)在这个区间上是＿＿＿＿函数，这个区间就叫做函数f(x)的＿＿＿区间；如果有f(x 1)＞f(x 2)，则称f(x)在这个区间上是＿＿＿＿函数，这个区间就叫做函数f(x)的＿＿＿区间； 〖说明〗1。

单调区间是定义域的子集；2。

若函数f(x)在区间D 上是增函数，则图象在D 上的部分从左到右呈＿＿趋势 若函数f(x)在区间D 上是减函数，则图象在D 上的部分从左到右呈＿＿趋势 3。

单调区间一般不能并 2、 判断单调性的方法：①定义； ②导数； ③复合函数单调性：同增则增，异增则减； ④图象 3、 常用结论：①两个增（减）函数的和为___；一个增（减）函数与一个减（增）函数的差是__； ②奇函数在对称的两个区间上有_____的单调性；偶函数在对称的两个区间上有_____的单调性；③互为反函数的两个函数在各自定义域上有______的单调性；【课前预习】1． 下列函数中，在区间(-∞，0)上是增函数的是 ( )A 、84)(2+-=x x x f B 、g(x)=ax+3 (a≥0) C 、2()1h x x =-+ D 、12()log ()s x x =- 2． 函数33y x x=+的单调递增区间是＿＿＿＿＿＿＿ 3． 函数f(x)＝｜log a x ｜（0＜a ＜1）的单调增区间是＿＿＿＿＿＿＿ 4． 函数)23(log )(221-+-=x x x f 的减区间是__________________5． 函数f(x)＝x 3+ax 有三个单调区间，则实数a 的取值范围是＿＿＿＿＿ 【例题讲解】例1：若函数2)1(2)(2+-+=x a x x f 在区间]4,(-∞上是减函数，则实数a 的取值范围是_________.【变式1】3211()(1)132f x x ax a x =-+-+在区间（1,4）内为减函数，在区间（6，＋∞）为增函数，求实数a 的取值范围；【变式2】已知数列{a n }中22(1)2n a n a n =+-+，且n a 随着n 的增大而增大，则实数a 的取值范围是＿＿＿＿＿＿＿例2、判断并证明函数1()1xf x x-=+的单调性【变式1】判断函数)1,0(11log )(≠>+-=a a x xx f a的单调性 【变式2】已知函数1()log (1)1axf x a x-=>+，是否存在实数x ，使关于x 的不等式 2()(1)f x f x <-成立例3、设)(x f 是定义在R 上的函数，对m 、R n ∈恒有)()()(n f m f n m f ⋅=+，且当0>x 时，1)(0<<x f 。

江苏省泰兴中学高一数学教学案(17)必修1_02 函数的单调性（1）班级 姓名目标要求1．理解函数的单调性以及相关概念；2．熟练运用函数单调性的定义判断和证明函数的单调性； 3．学会根据函数单调性的定义和图象求一些简单函数的单调区间．重点难点重点：函数的单调性的证明和判断； 难点：函数单调性的概念及单调性的应用．课前预习1．画出2y x =的图象，观察（1）x ∈[)+∞,0;（2）x ∈(]0,∞-;（3）x ∈（-∞，+∞） 当x 的值增大时，y 值的变化情况。

2．观察实例：课本P34的实例，怎样用数学语言刻画上述时间段内“随着时间的推移气温逐渐升高”这一特征？3．增函数：设函数)(x f y =的定义域为A ，区间A I ⊆，若对于区间I 内的 ，当 时都有 ，称函数)(x f y =在 是单调增函数，I 为 图象示例：4．减函数：设函数)(x f y =的定义域为A ，区间A I ⊆，若对于区间I 内的 ，当 时，都有 ，则称函数)(x f y =在 是单调减函数，I 为 图象示例：5．单调性：函数)(x f y =在 上是 ，则称)(x f y =在 具有单调性6. 单调区间： ．课堂互动例1 画出下列函数的图象，并写出单调区间： （1）221y x x =-++ （2）21-=x y （3）|21|y x =-变题1：作出函数223y x x =--的图象，并写出函数的单调区间．例2 证明：函数xx x f 1)(+=在（０，１）上是单调减函数．例3 变题函数5)2(22+-+=x a x y 在),4(+∞上是增函数，求实数a 的取值范围.变题：函数54)(2+-=mx x x f 在),2[+∞-上是增函数，在]2,(--∞上是减函数，求函数)(x f 的解析表达式．例4 已知)(x f y =在定义域)1,1(-上是减函数，且),13()1(-<-a f a f 求实数 a 的取值范围．例5 求函数6)(2-+=x x x f 的单调区间．课堂练习1、如图,已知函数)(x f y =,)(x g y =的图像,根据图像说出函数)(x f y =,)(x g y =的单调增 区间xy3π32π32π-O()y g x =y1y = f ( x )2、填表：函 数xky =（0≠k ） kx y =（0≠k ）0>k0<k0>k0<k单调区间 （－∞，+∞） 单调性增函数3、二次函数c bx ax y ++=2（0a ≠），的单调性是：当a > 0 时，在区间________上递增，在区间__________上递减；当a < 0 时，在区间__________上递增，在区间_______上递减．学习反思1、利用定义证明或判断函数的单调性的一般步骤：2、求函数单调区间的常用方法：3、求复合函数单调区间的步骤：江苏省泰兴中学高一数学作业(17)班级 姓名 得分1、在区间),0(+∞上是减函数的是________________. (1) 2x y = (2)32-=x y (3) xy 1=(4) x y =2、若函数)(x f 是实数集R 上的增函数，a 是实数，则下面不等式中正确的是______. (1))1()(2->a f a f (2))3()(a f a f < (3))()(22a f a a f >+ (4))()1(22a f a f <-3、已知函数f (x )= x 2－2x ＋2，那么f (1)，f (－1)，f 3之间的大小关系为 .4、函数2212)(a ax x x f +-+-=在区间]2,(-∞上是增函数，在区间),2[+∞上是减函数，则=)2(f ______．5、已知函数f （x ）＝x 2－2ax ＋a 2＋1在区间（－∞，1）上是减函数，则a 的取值范围是 ．6、已知31()2x f x x +=+，指出()f x 的单调区间. ． 7、132+--=x x y 在区间),(a -∞上是增函数，则实数a 的取值范围是__ __ . 8、函数()y f x =的递增区间是()2,3-，则(5)y f x =+的递增区间是 ． 9、画出下列函数的图像，并根据图像说出)(x f y =的单调区间，以及在各单调区间上，函数)(x f y =是增函数还是减函数：（1）2|56|y x x =-+； （2）211x y x -=-（3）21,01,0x x y x x ⎧+≥=⎨--<⎩10、求证： 函数1)(3+--=x x x f 在),(+∞-∞是减函数.11、函数4)25()(22-+--=a x a ax x f 在),2[+∞上是增函数，求实数a 的取值范围.12、已知函数1()2ax f x x +=+在区间()+∞-,2上是增函数，试求a 的取值范围．。

1.函数221y x 单调减区间是_________________．2.若函数2()(1)5f x x a x 在区间1(,1)2上具有单调性，则实数a 的取值范围是______ ．3.已知函数()f x 是定义在[1,1]上的增函数，且(1)(13)f x f x ，则实数x 的取值范围是_________________________．4.已知()f x 在(,)内是减函数，,a b R ，且0a b ，设()()A f a f b ，()()B f a f b ，则A,B 的大小关系是_________________．5.若函数+by ax y x 与在（0，）上都是减函数，则2(0,)y ax bx 在上是______ ．（填“增函数”或“减函数”）6.函数212()log (43)f x x x 的递减区间是________________．7.已知函数log (2)a y ax 在[0，1]上单调递减，则a 的取值范围是_________．8.已知函数(0)()(3)4(0)xa x f x a x a x 满足对任意的12x x ，都有1212()()0f x f x x x 成立，则a 的取值范围是_________．9.已知函数()f x 是定义在(0,)上的减函数，且满足()()()f xy f x f y ，(2)1f ，若()(2)2f x f x ，求x 的取值范围．1.11(,)+22和（，）2.(,2][3,)3.1[0,)24.A B5.减函数6.(1,2]7.(1,2)8.1(0,]49解：()+0020()()()(2)12,(4)2()(2)2[(2)](4)()+5155f x xx xf xy f x f y f xy f f x f x f x x f f x x Q Q 函数定义域是（0，）①由且取得由得又在（0，）上递减，x(2+x)<4-1-②由①②知，x 的取值范围是0<x<-1+。

学案7 函数的单调性一、课前准备： 【自主梳理】1． 函数单调性的定义：（1） 一般地，设函数()y f x =的定义域为A ，区间I A ⊆．如果对于区间I 内的任意两个值1,2x x ，当12x x <时，都有_______________,那么就说()y f x =在区间I 上是单调增函数，I 称为()y f x =的___________________．如果对于区间I 内的任意两个值1,2x x ，当12x x <时，都有_______________,那么就说()y f x =在区间I 上是单调减函数，I 称为()y f x =的___________________．（2） 如果函数()y f x =在区间I 上是单调增函数或单调减函数，那么就说()y f x =在区间I 上具有___________性，单调增区间或单调减区间统称为____________________． 2.复合函数的单调性：对于函数()(),y f u u g x ==和如果当(,)(,),()x a b u m n u g x ∈∈=时，且在区间(,)a b 上和()y f u =在区间(,)m n 上同时具有单调性，则复合函数[()]y f g x =在区间(,)a b 上具有__________，并且具有这样的规律：___________________________． 3.求函数单调区间或证明函数单调性的方法：（1）______________； (2)____________________； (3)__________________ ．【自我检测】1.函数(,)y kx b k b =+是常数在R 上是减函数，则k 的取值范围是___________．2.函数2()1f x x =-在(0,)+∞上是_____函数（填“增”或“减”）． 3.函数12y x=+的单调区间是_____________________． 4.函数()y f x =在定义域R 上是单调减函数，且(1)(2)f a f a +>，则实数a 的取值范围是________________________．5.已知函数()f x 在区间(0,)+∞上是增函数，则23(1)()4f a af -+与的大小关系是_______ ．6.函数()f x =___________________．二、课堂活动： 【例1】填空题：（1） 若函数()f x 的单调增区间是(2,3)-，则(5)y f x =+的递增区间是_________． （2） 函数2y x x =-+的单调减区间是________________． （3） 若1()-+2ax f x x +=∞+在（2，）上是增函数，则a 的取值范围是_____________． （4） 若(31)4,1()log ,1a a x a x f x x x -+≤⎧=⎨>⎩是R 上的减函数，则a 的取值范围是_________． 【例2】求证：函数2()1xf x x=+在区间[1,)+∞上是减函数．【例3】已知函数()f x 对任意的,a b R ∈，都有()()()1f a b f a f b +=+-，且当0x >时，()1f x >．（1） 求证：()f x 是R 上的增函数；（2） 若(4)5f =，解不等式2(32)3f m m --<．课堂小结三、课后作业1.函数221y x =-单调减区间是_________________． 2.若函数2()(1)5f x x a x =--+在区间1(,1)2上具有单调性，则实数a 的取值范围是______ ．3.已知函数()f x 是定义在[1,1]-上的增函数，且(1)(13)f x f x -<-，则实数x 的取值范围是_________________________．4.已知()f x 在(,)-∞+∞内是减函数，,a b R ∈，且0a b +>，设()()A f a f b =+，()()B f a f b =-+-，则A,B 的大小关系是_________________．5.若函数+by ax y x==-∞与在（0，）上都是减函数，则2(0,)y a x b x =++∞在上是______ ．（填“增函数”或“减函数”） 6.函数212()log (43)f x x x =-+-的递减区间是________________．7.已知函数log (2)a y ax =-在[0，1]上单调递减，则a 的取值范围是_________．8.已知函数(0)()(3)4(0)x a x f x a x a x ⎧<=⎨-+≥⎩满足对任意的12x x ≠，都有1212()()0f x f x x x -<-成立，则a 的取值范围是_________．9.确定函数()f x =10.已知函数()f x 是定义在(0,)+∞上的减函数，且满足()()()f xy f x f y =+，(2)1f =，若()(2)2f x f x ++>，求x 的取值范围．学案7 函数的单调性（答案）一、课前准备： 【自主梳理】1.（1）12()()f x f x <，单调增区间，12()()f x f x >，单调减区间，（2）单调，单调区间2.单调性，同则增异则减3.（1）定义法 （2）图象法 （3）导函数法【自我检测】1.(,0)-∞ 2 .增 3. (,0)-∞和(0,)+∞ 4. (1,)+∞ 5. 23(1)()4f a a f -+≥ 6.(,1]-∞ 二、课堂活动： 【例1】（1）(7,2)-- （2）11[,0],[,)22-+∞ （3）1(,)2+∞ (4)11[,)73【例2】证明：设1212,[1,),x x x x ∈+∞<且22121221122222121212122212(1)(1)()()11(1)(1)()(1)(1)(1)x x x x x x f x f x x x x x x x x x x x +-+-=-==++++--=++1212121222121212,[1,),,0,10(1)(1)0()()0,()()x x x x x x x x x x f x f x f x f x ∈+∞<∴-<-<++>∴->>∴且又，即函数在区间上是减函数【例3】（1）证明：12212121211211,0,()1()[()]()()1()()R x x x x f x x f x f x x x f x f x x f x f x <->∴->∴=+-=+-->∴任取则是上的增函数（2）解：2222,(4)2(2)15,(2)3(32)3(32)(2)()432213a b f f f f m m f m m f f x R m m m ===-=∴=∴--<--<∴--<⇒-<<取则不等式即为由（1）知在上递增三、课后作业1.11(,)+22-∞∞和（，）2.(,2][3,)-∞⋃+∞3.1[0,)24.A B <5.减函数6.(1,2]7.(1,2)8. 1(0,]49.解：定义域为1(,)2-∞，任取121,(,)2x x ∈-∞，且12x x <12()()0f x f x -===<12()()1()2f x f x f x ∴<∴∞在（-,）上单调递增10.解：()+0020()()()(2)12,(4)2()(2)2[(2)](4)()+1f x x x x f xy f x f y f x y f f x f x f x x f f x x ∞>⎧∴⇒>⎨+>⎩=+====++>+>∞∴∴<<-函数定义域是（0，）①由且取得由得又在（0，）上递减，x(2+x)<4②由①②知，x 的取值范围是。

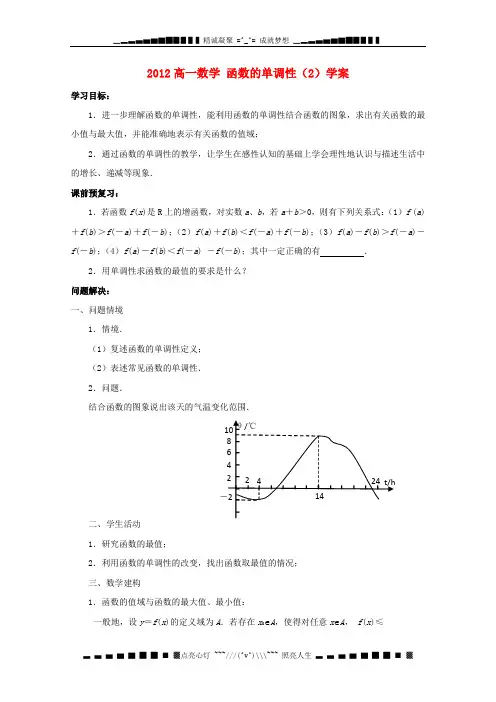
2012高一数学函数的单调性（2）学案学习目标：1．进一步理解函数的单调性，能利用函数的单调性结合函数的图象，求出有关函数的最小值与最大值，并能准确地表示有关函数的值域；2．通过函数的单调性的教学，让学生在感性认知的基础上学会理性地认识与描述生活中的增长、递减等现象．课前预复习：1．若函数f(x)是R上的增函数，对实数a、b，若a＋b＞0，则有下列关系式：（1）f (a)＋f(b)＞f(－a)＋f(－b)；（2）f(a)＋f(b)＜f(－a)＋f(－b)；（3）f(a)－f(b)＞f(－a)－f(－b)；（4）f(a)－f(b)＜f(－a) －f(－b)；其中一定正确的有．2．用单调性求函数的最值的要求是什么？问题解决：一、问题情境1．情境．（1）复述函数的单调性定义；（2）表述常见函数的单调性．2．问题．结合函数的图象说出该天的气温变化范围．二、学生活动1．研究函数的最值；2．利用函数的单调性的改变，找出函数取最值的情况；三、数学建构1．函数的值域与函数的最大值、最小值：一般地，设y＝f(x)的定义域为A．若存在x0∈A，使得对任意x∈A， f(x)≤f (x 0)恒成立，则称f (x 0)为y ＝f (x )的最大值，记为y max ＝f (x 0)．若存在定值x 0∈A ，使得对任意x ∈A ，f (x )≥f (x 0)恒成立，则称f (x 0)为y ＝f (x )的最小值，记为y min ＝ f (x 0)．注：（1）函数的最大值、最小值分别对应函数图象上的最高点和最低点，典型的例子就是二次函数y ＝ax 2＋bx －c (a ≠0)，当a ＞0时，函数有最小值；当a ＜0时，函数有最大值．（2）利用函数的单调性，并结合函数的图象求函数的值域或函数的最值是求函数的值域或函数的最值的常用方法．2．函数的最值与单调性之间的关系：已知函数y ＝f (x )的定义域是[a ，b ]，a ＜c ＜b ．当x ∈[a ，c ]时，f (x )是单调增函数；当x ∈[c ，b ] 时，f (x )是单调减函数．则f (x )在x ＝c 时取得最大值．反之，当x ∈[a ，c ]时，f (x )是单调减函数；当x ∈[c ，b ] 时，f (x )是单调增函数．则f (x )在x ＝c 时取得最小值． 练习反馈：例1、求出下列函数的最小值：（1）y ＝x 2－2x ；（2）y ＝1x，x ∈[1，3]．变式：（1）将y ＝x 2－2x 的定义域变为(0，3]或[1，3]或[－2，3]，再求最值． （2）将y ＝1x的定义域变为(－2，－1]，(0，3]结果如何？跟踪练习：求f (x )＝－x 2＋2x 在[0，10]上的最大值和最小值．例2、求函数f (x )＝x 2－2ax 在[0，4]上的最小值． 课堂小结：利用图形，感知函数的单调性→证明一个函数的单调性→确定一个函数的最值→确定一个函数的值域．课后巩固：1.已知函数y ＝f (x )的定义域为[a ，b ]，a ＜c ＜b ．当x ∈[a ，c ]时，f (x )是单调增函数；当x ∈[c ，b ]时，f (x )是单调减函数．试证明f (x )在x ＝c 时取得最大值．变式：已知函数y＝f(x)的定义域为[a，b]，a＜c＜b．当x∈[a，c]时，f(x)是单调减函数；当x∈[c，b]时，f(x)是单调增函数．试证明f(x)在x＝c时取得最小值．2.如图，已知函数y＝f(x)的定义域为[－4，7]，根据图象，说出它的最大值与最小值．3.求下列函数的值域：（1）yx∈[0，3]；（2） y＝11x-，x∈[2，6]；（3）y（4）y＝11(1)x x--．学习反思：。

＝ （x1x2－a）。
当0<x1<x2< 时，0<x1x2<a，又x1－x2<0，
∴ ，即 ，
∴函数 在（0， ）上是减函数。
当 <x1<x2时，x1x2>a，又x1－x2<0，
∴f（x1）－f（x2）<0，即f（x1）<f（x2），
∴函数f（x）在（ ，＋∞）上是增函数。
例题1若函数f（x）＝ 在（－∞，－1）上是减函数，求实数a的取值范围。
二、解答题
9. 设 是定义在R上的函数，对 、 恒有 ，且当 时， 。
（1）求证： ；
（2）证明： 时恒有 ；
（3）求证： 在R上是减函数；
（4）若 ，求 的取值范围。
1. 2 解析：画出 的图象如下：
由图可知， 的最小值是2。
2.
解析：画出分段函数 的图象如下：
而 ，观察图象可知满足 的解集。
3. （1） ；（2）
，即 ，
∴ 在 上是增函数。
技巧点拨：对于抽象函数（未给出具体解析式的函数）的求值问题，需要根据题目给出的已知条件进行灵活赋值，求出需要求的函数值；抽象函数单调性的证明仍然采用单调性的定义以及结合题目已知来进行。
【综合拓展】
巧用函数单调性解不等式
◆解函数不等式问题的一般步骤：
①确定函数f（x）在给定区间上的单调性；
由图可知： ，∴ 。
7. （1） ；（2）
解析：（1）画出符合题意的 的图象如下图：
由图可知：二次函数 的对称轴直线方程为 ，
∴ ， 。
又∵ ，
∴ 。
（2）
画出 的图象如下图：
∵ ，又∵ ，
∴ ，
解得： 。

函数的单调性【学习要求】函数的基本性质B【学习目标】1．理解函数的单调性 2．能判断或证明函数的单调性【学习重难点】判断或证明函数的单调性【要点梳理】函数单调性的定义：设函数()f x 的定义域为A ，区间I A ⊆，如果对于区间I 上的任意两个值12,x x ，当__________时，都有_____________，称()y f x =在区间I 上是单调增函数，I 称为()y f x =的增区间如果对于区间I 上的任意两个值12,x x ，当__________时，都有_____________，称()y f x =在区间I 上是单调减函数，I 称为()y f x =的减区间【基础自测】1．判断下列说法是否正确：（1）若定义在R 上的函数()f x 满足(2)(1)f f >，则函数()f x 是R 上的单调增函数；（2）若定义在R 上的函数()f x 满足(2)(1)f f >，则函数()f x 在R 上不是单调减函数；（3）若定义在R 上的函数()f x 在区间(,0]-∞上是单调增函数，在区间[0,)+∞上是单调增函数，则函数()f x 在R 上是单调增函数；（4）若定义在R 上的函数()f x 在区间(,0]-∞上是单调增函数，在区间(0,)+∞上是单调增函数，则函数()f x 在R 上是单调增函数。

2．下列函数 （1）2()(1)f x x =- （2）()x f x e = （3）()ln(1)f x x =+ （4） 111y x =-- （5）||y x x =在(,0)x ∈-∞是减函数的序号是_________________4．（1） 函数32()15336f x x x x =--+的单调递增区间为 。

（2） 函数20.7log (32)y x x =-+的单调减区间是____________________5．若2()2f x x ax =-+与1()2ax g x x +=+在区间(2,)-+∞上是减函数，则a 的取值范围是_______________ 【学习过程】一、典例精讲：例1 （1）判断函数()f x =的单调性，并证明你的结论； （2）判断函数1()ln1x f x x-=+的单调性，并证明你的结论。

二．师生互动
三．建构数学
1.增函数与减函数：
2．函数的单调性与单调区间：
四．数学应用
例1.画出下列函数的图像，并写出单调区间。
例2求证：函数f(x)＝－ －1在区间(－∞，0)上是单调增函数．
总结用单调性定义证明的步骤：
【当堂练习】
书本第37页1，2，5，6，7
【课后巩固】
课时训练
【课后反思】Байду номын сангаас
【教学重难点】
1.重点：理解函数的单调性的定义
2.难点：用定义判断或证明函数在某个区间上的单调性
【教学准备】）
多媒体
【教学活动】
1 问题情境
2 师生互动
3 建构数学
4 数学应用
5 课堂练习
【教学反思】
【学生活动】
【学习目标】
1．通过图像直观地认识函数的单调性，并理解函数的单调性的定义。
2．根据图像能够判断单调性，写出单调区间。
3．能够用定义判断或证明函数在某个区间上的单调性。
【课时安排】
1课时
【课前预习】
初中所学的常见函数的图像该如何画？
【课堂探究】
一．问题情境
如图（课本34页图2―1―13），是气温关于时间t的函数，记为＝f(t)，观察这个函数的图象，说出气温在哪些时间段内是逐渐升高的或是下降的？
问题：怎样用数学语言刻画上述时间段内“随时间的增加气温逐渐升高”这一特征？
执笔人：夏文秀审核人：2011年9月日
第二章2.1.3函数的单调性第5课时
【教师活动】
【教学目标】
1．在初中学习一次函数、二次函数的性质的基础上，进一步感知函数的单调性，并能结合图形，认识函数的单调性
2.用图像直观地认识函数的单调性，理解函数单调性的定义。

2019-2020学年苏教版数学精品资料第六课时函数的单调性（2）【学习目标】1．熟练掌握证明函数单调性的方法；2．会证明一些较复杂的函数在某个区间上的单调性； 3．能利用函数的单调性解决一些简单的问题．【重点】证明函数单调性的方法；【难点】利用函数的单调性解决一些简单的问题。

【活动过程】活动一：回顾判断或证明函数单调性的步骤1．复习回顾函数单调性的有关知识与方法：2. 判断函数xxx f 1)(在（０，１）的单调性.．3.求证：函数2()1f x xx 在R 上是单调减函数．活动二：函数的最值设函数)(x f y 的定义域为A ，如果存在A x 0，使得对于，都有，则称)(0x f 则称函数)(x f y的最大值，记为；如果存在A x 0，使得对于，都有，则称)(0x f 则称函数)(x f y的最小值，记为。

例1．下列函数的最小值：（1）x2xy2（2）]3,1[x ,x1y（3）y=kx －2 ( k0),]3,1[x 例2．求函数32)(2x xx f 分别在下列区间上的最值：（1）]3,1[x；（2）]1,2(x；（3）[2,]x a ；（4）]2,[t t x 。

变1：函数32)(2x xx f 在区间]2,[tt 上有最大值3，求t 的取值集合。

变2：求函数232)(2xx xx f 在区间]2,1-[上有最小值。

例3．已知函数)(x f 的定义域是b c a b a ],,[，当],[c a x 时，)(x f 是单调增函数，当],[b c x时，)(x f 是单调减函数，试证明)(x f 在c x时取得最大值。

归纳总结：活动三：已知函数单调性，求参数范围例4、若函数2()45f x xmx m 在[2,)上是增函数，在(,2]上是减函数，则实数m 的值为；变1：若函数2()45f x xmx m 在[2,)上是增函数，则实数m 的取值范围为；变2：若函数2()45f x xmx m 的单调递增区间为[2,)，则实数m 的值为．例5、已知函数()y f x 的定义域为R ，且对任意的正数d ，都有()()f xd f x ，求满足(1)(21)f a f a 的a 的取值范围．变：若函数1)(x axx f 在区间（，1）上是增函数，试求a 的取值范围活动四：求复合函数的单调区间例6、已知函数()f x 是R 上的减函数，2()4g x xx ，求函数()[()]H x f g x 的单调递区间.变1：求函数228)(x x x f 的单调区间。

二．证明函数的单调性：
例2：求证：函数 在 上是单调减函数．
【证明】
设 ，则
，
∵ ，∴ ；
∵ ，∴ ，
同理 ，
∴ ，∴ ，即 ，
∴ 在 上是单调减函数．
例３：(1)若函数 在 上是增函数，在 上是减函数，则实数 的值为；
（2）若函数 在 上是增函数，则实数 的取值范围为；
（3）若函数 的单调递增区间为 ，则实数 的值为．
函数的单调性（2）
一．较复杂函数的单调性证明：
例1：判断函数 的单调性，并用单调性的定义证明你的结论．
【证明】函数 是增函数．证明如下：
设 ，则
，
∵ ，∴ ， ，∴ ，
即 ，∴函数 是增函数．
说明：本题中的函数 可视作函数 和 的和，这两个函数在 内都是增函数， 也是增函数．由此可见：如果两个函数在同一区间上都是增（减）函数，那么它们的和也是增函数。
追踪训练
1．已知函数 和 在 上都是减函数，则 在 上（A）
是增函数
是减函数
既不是增函数也不是减函数
的单调性不能确定
2.若函数 在区间 上是减函数，则实数 的取值范围是 ．
3.若 在 上是增函数，且 ，则 ＞ ．
（注：从 、 、 中选择一个填在横线上）
4.函数 函数单调性的定义证明：函数 在 上是增函数．
证明：设
∴
即
故函数 在 上是增函数．
【师生互动】
学生质疑
教师释疑
3.函数y=|x+1|的单调递减区间为[－1，+∞)单调递减区间(－∞，－1]
已知函数单调性，求参数范围：
例4:已知函数 的定义域为 ，且对任意的正数 ，都有 ，求满足 的 的取值范围．

课题 函数的单调性【考点聚焦】1、理解函数单调性的定义，并学会利用定义去判断或证明函数在给定区间上的单调性2、理解函数的单调性、最大(小)值的几何意义，会用单调性方法求函数的最大(小)值3、能利用函数的单调性解决其他一些综合问题.【考情预测】1、函数单调性仍将会是2016年高考的重点，特别要注意函数单调性的应用.2、常见题型有：（1）求函数的单调区间；（2）用定义判断函数在所给区间上的单调性；（3）单调性的应用的意识，特别是求函数最值，（4）已知函数的单调性求参数的范围等【重点难点】研究函数的单调性的工具选择：图像、定义、导数【教学过程】一、知识要点（1）单调增函数 关键词：任意两个值（2）单调减函数（3）单调性、单调区间（4）几何意义：二、基础训练1、已知函数t x m x f +-=)12()(在区间R 是减函数.则m 的范围2、已知函数14)(2+=mx x x f －在区间).2[∞+-是增函数.则m 的范围3、函数||)3(x x y -=的单调递减区间是______4、函数1212)(+-=x x x f 在R 上为 函数（增减性） 5、已知函数12)(-+=x a x x f 在),1(+∞上是减函数.则a 的范围 6、函数xx y 1ln -=的单调增区间7、已知函数xa x x f +=)(在),1(+∞上是增函数. 则a 的范围 8、已知函数,1()(3)4,1x a x f x a x a x ⎧<=⎨-+≥⎩，若对任意的12x x ≠都有1212()()0f x f x x x -<-成 立，则a 的取值范围为______________9、函数x x x f --+=11)(的最大值M ,最小值m ，则m M = 10、已知函数2()cos f x x x =-，对于]2,2[ππ-上的任意12x x ，，有如下条件：①12x x >； ②2212x x >；③12x x >．其中能使12()()f x f x >恒成立的条件序号是 三、典型例题例1、求82)(2--=x x x f 的单调增区间例2、确定函数x x f 211)(-=在定义域上的单调性 例3、若()f x 对任意的,m n R ∈都有()()()1,f m n f m f n +=+-且0,x >恒有()1f x >.（1）求证：()f x 在R 上是增函数 （2）若(3)4f =，解不等式2(2)2f a a +-< 例4、已知函数11lg )(--=x kx x f (1) 求函数)(x f 的定义域； (2) 若函数)(x f 在[10，＋∞)上单调递增，求k 的取值范围例5、已知(]1,0,12)(2∈-=x xax x f （1）若()x f 在区间]1,0(是增函数，求a 的取值范围（2）求()x f 在区间]1,0(上的最大值小结：（1）利用定义证明函数单调性的步骤：⑴取值 ⑵作差 ⑶作差 ⑷化积与0比较 ⑸结论.（2）判定函数的单调性的工具：（1）图象法；（2）定义法；（3）导数四、课堂检测1、已知函数2)(2+++=m x mx x f 在(－∞，2)上是增函数，则实数m 的范围_______2、函数43()21x f x x -=+的单调减区间为 3、已知函数)(x f 在)1,1(-上是减函数，若)9()3(2a f a f -<-，则a 的范围4、已知函数2)(+-=b x a x f 在),1(+∞上是增函数. 则a 的范围 b 范围5、已知函数()f x 为定义在(2,2)-上的偶函数，且()f x 在(2,0]-上递增，则满足不等式 (1)(2)f a f a ->的a 的取值范围为___________6、已知函数⎩⎨⎧>-≤-=0,)1(0,2)(x x k x k e x f x 是R 上的增函数，则实数k 的取值范围_______7、函数⎩⎨⎧<-≥+=0,)1(0,1)(22x e a x ax x f ax 在R 上单调，则a 的取值范围是_____ 8、若函数2()log ()a f x x ax =-在区间1(,0)2-内递增，则a 的取值范围为_________ 9、讨论函数1)(2-=x ax x f 在)1,1(-上的单调性，并证明 10、已知函数2()21x x m f x +=-为奇函数. (1) 求实数m 的值 (2) 用定义证明函数()f x 在区间(0,)+∞上为增函数(3) 若关于x 的不等式()0f x a +<对区间[]1,3上的任意实数x 都成立，求实数a 的范围11、是否存在实数a ，使函数)(log )(2x ax x f a -=在区间]4,2[上是增函数？如果存在，说明a 可取哪些值；如果不存在，请说明理由12、设函数a ax x e x f x++=2)(其中a 为实数(1) 若)(x f 定义域为R ，求a 的范围 （2）当)(x f 定义域为R 时，求)(x f 的单调减区间。

2012高一数学 函数的单调性（1）学案学习目标：1．在初中学习一次函数、二次函数的性质的基础上，进一步感知函数的单调性，并能结合图形，认识函数的单调性；2．通过函数的单调性的教学，渗透数形结合的数学思想，并对学生进行初步的辩证唯物论的教育；3．通过函数的单调性的教学，让学生学会理性地认识与描述生活中的增长、递减等现象． 课前预复习： （1）函数xx f 3)(=的递减区间是 （2）设函数的范围上否认减函数，则是a R b x a x f +-=)12()( （3）函数单调性的定义是什么？单调区间是什么定义的？ 问题解决：一、问题情境如图（课本34页图2―1―13），是气温θ关于时间t 的函数，记为θ＝f (t )，观察这个函数的图象，说出气温在哪些时间段内是逐渐升高的或是下降的？问题：怎样用数学语言刻画上述时间段内“随时间的增大气温逐渐升高”这一特征？二、学生活动1．结合图2―1―13，说出该市一天气温的变化情况； 2．回忆初中所学的有关函数的性质，并画图予以说明；))3．结合右侧四幅图，解释函数的单调性． 三、数学建构 1．增函数与减函数：一般地，设函数y ＝f (x )的定义域为A ，区间I A ．如果对于区间I 内的任意两个值x 1、x 2，当x 1＜x 2时，都有f (x 1)＜f (x 2)，那么就说y ＝f (x )在区间I 是单调增函数，区间I 称为y ＝f (x )的单调增区间．如果对于区间I 内的任意两个值x 1、x 2，当x 1＜x 2时，都有f (x 1)＞f (x 2)，那么就说y ＝f (x )在区间I 是单调减函数，区间I 称为y ＝f (x )的单调减区间．2．函数的单调性与单调区间：如果函数y ＝f (x )在区间I 是单调增函数或单调减函数，那么就说函数y ＝f (x )在区间I 上具有单调性．单调增区间与单调减区间统称为单调区间．注：一般所说的函数的单调性，就是要指出函数的单调区间，并说明在区间上是单调增函数还是单调减函数． 练习反馈：例1：画出下列函数的图象，结合图象说出函数的单调性．1．y ＝x 2＋2x －12．y ＝2x例2：求证：函数f (x )＝－1x－1在区间(－∞，0)上是单调增函数．例3：说出下列函数的单调性并证明． 1．y ＝－x 2＋2 2．y ＝2x＋1课堂小结：利用图形，感知函数的单调性→给出单调性的严格意义上的定义→证明一个函数的单调性．课后巩固：1．已知函数f(x)＝2x 2＋(2m －1)x ＋3是偶函数，则函数f(x)在区间[－1，2]内的单调性为2．函数y ＝log (x 2－1)的单调递增区间为3．已知函数f(x)＝2x 2＋(3―m)x ―5在（－∞，－1]上单调递减，则实数m 的取值范围为_____________变题：已知函数f(x)＝2x 2＋(3―m)x ―5在[-1,1]上单调函数，则实数m 的取值范围为_____________4．已知偶函数f(x)在（－∞，0]上为减函数，且f(31)＝0，则不等式xf(x)<0的解集为___________。

第七课时 函数的单调性（2）【学习导航】学习要求1．熟练掌握证明函数单调性的方法；2．会证明一些较复杂的函数在某个区间上的单调性；3．能利用函数的单调性解决一些简单的问题．【精典范例】一．较复杂函数的单调性证明：例1：判断函数21()f x x x =-((0,))x ∈+∞的单调性，并用单调性的定义证明你的结论．说明：本题中的函数()f x 可视作函数2y x =和1y x=-的和，这两个函数在(0,)+∞内都是增函数，()f x 也是增函数．由此可见：如果两个函数在同一区间上都是增（减）函数，那么它们的和也是增函数。

二．证明函数的单调性：例2：求证：函数()f x x =在R 上是单调减函数．例３：(1)若函数2()45f x x mx m =-+-在[2,)-+∞上是增函数，在(,2]-∞-上是减函数，则实数m 的值为 ；（2）若函数2()45f x x mx m =-+-在[2,)-+∞上是增函数，则实数m 的取值范围为 ；（3）若函数2()45f x x mx m =-+-的单调递增区间为[2,)-+∞，则实数m 的值为 ．追踪训练一1. 函数()f x 是定义域上单调递减函数，且过点(3,2)-和(1,2)-，则|()|2f x <的自变量x 的取值范围是（ ）听课随笔()A (3,)-+∞ ()B (3,1)-()C (,1]-∞ ()D (,)-∞+∞2. 已知函数f (x )是区间(0，＋∞)上的减函数，那么f (a 2－a ＋1)与3()4f 的大小关系是 ．3. 函数y=|x+1|的单调递减区间为___________ 单调递减区间 _____________________【选修延伸】已知函数单调性，求参数范围：例4: 已知函数()y f x =的定义域为R ，且对任意的正数d ，都有()()f x d f x +<，求满足(1)(21)f a f a -<-的a 的取值范围．点评:注意函数的单调区间是定义域上的区间，也就是说函数的单调区间一定是函数定义域的子集。

导数在研究函数中的应用【学习目标】1了解函数单调性和导数的关系,能利用导数研究函数的单调性,会求函数的单调区间多项式函数一般不超过三次｡2了解函数在某点取得极值的必要条件和充分条件,会用导数求函数的极大值､极小值多项式函数一般不超过三次及最大最小值｡【学习重难点】1．学习重点：了解函数单调性和导数的关系；能利用导数研究函数的单调性，会求函数的单调区间，对多项式函数一般不超过三次；了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值2．学习难点：对多项式函数一般不超过三次；会求闭区间上函数的最大值、最小值，对多项式函数一般不超过三次．【学习过程】一､自主梳理1导数和函数单调性的关系:1对于函数=f,如果在某区间上f′>0,那么f为该区间上的________;如果在某区间上f′2,则函数f=错误!X³-a21在区间0,2上有________个零点｡的导函数f′的图象如图所示,给出以下结论:①函数f在-2,-1和1,2上是单调递增函数;②函数f在-2,0上是单调递增函数,在0,2上是单调递减函数;③函数f在=-1处取得极大值,在=1处取得极小值;④函数f在=0处取得极大值f0｡则正确命题的序号是________｡填上所有正确命题的序号｡=X³m2m61既存在极大值又存在极小值,则实数m的取值范围为________｡二､解答题共42分912分求函数f=错误!的极值｡1014分2021·秦皇岛模拟已知a为实数,且函数f=2-4-a｡1求导函数f′;2若f′-1=0,求函数f在[-2,2]上的最大值､最小值｡1116分已知函数f=X³m2n-2的图象过点-1,-6,且函数g=f′6的图象关于轴对称｡1求m,n的值及函数=f的单调区间;2若a>0,求函数=f在区间a-1,a1内的极值｡答案自主梳理11增函数减函数 2增减 21①f′>0f′0 2②f′=0③f′=0 极大值极小值 31极值2fA,fB自我检测1③ 22,∞ 3[-3,∞ 4充要课堂活动区例1 解题导引 1一般地,涉及到函数尤其是一些非常规函数的单调性问题,往往可以借助导数这一重要工具进行求解｡函数在定义域内存在单调区间,就是不等式f′>0或f′0,即-22e>0, ∵e>0,∴-22>0,解得-错误!错误!错误!错误!∴-2a-2a≥0对∈-1,1都成立,即2-a-2-a≤0对∈-1,1恒成立｡设h=2-a-2-a,只需满足错误!,解得a≥错误!｡3若函数f在R上单调递减,则f′≤0对∈R都成立,即[-2a-2a]e≤0对∈R都成立｡∵e>0,∴2-a-2-a≥0对∈R都成立｡4≤0,这是不可能的｡∴Δ=a-224a≤0,即a2故函数f不可能在R上单调递减｡若函数f在R上单调递增,则f′≥0对∈R都成立,即[-2a-2a]e≥0对∈R都成立｡∵e>0,∴2-a-2-a≤0对∈R都成立｡而2-a-2-a≤0不可能恒成立,故函数f不可能在R上单调递增｡综上可知函数f不可能是R上的单调函数｡变式迁移1 解 1由题意得f′=3221-a-aa2,又错误!,解得b=0,a=-3或a=12由f′=0,得=a,2=-错误!｡1又f在-1,1上不单调,即错误!错误!错误!错误!错误!错误!错误!错误!错误!错误!时,g′0,从而g在区间-错误!,错误!上是增函数｡由前面讨论知,g在区间[1,2]上的最大值与最小值只能在=1,错误!,2时取得, 而g1=错误!,g错误!=错误!,g2=错误!｡因此g在区间[1,2]上的最大值为g错误!=错误!,最小值为g2=错误!｡课后练习区10,1 40,∞0,即a0,∴错误!4,易知f在0,2上为减函数,且f0=1>0,f2=错误!-4a错误!0, ∴m>6或m0,故=-2是函数的极小值点,故f的极小值为f-2=-错误!;当∈-2,1时f′>0,当∈1,∞时f′0,得>2或<0,故f的单调递增区间是-∞,0∪2,∞;由f′<0,得0<<2,故f的单调递减区间是0,2｡2由1得f′=3-2,令f′=0,得=0或=2当变化时,f′､f的变化情况如下表:-∞,00 0,2 2 2,∞f′0 - 0由此可得:当0<a<1时,f在a-1,a1内有极大值f0=-2,无极小值; 当a=1时,f在a-1,a1内无极值;当1<a<3时,f在a-1,a1内有极小值f2=-6,无极大值; 当a≥3时,f在a-1,a1内无极值｡综上得:当0<a<1时,f有极大值-2,无极小值;当1<a<3时,f有极小值-6,无极大值;当a=1或a≥3时,f无极值｡。