材料力学--截面的几何性质答案

截面几何性质 作业专业班级 姓名 学号1. 判断题（1）任意平面图形至少有1对形心主惯性轴，等边三角形有3对形心主惯性轴。

（ × ） （2）平面图形的几何性质中，静矩和惯性矩的值可正、可负、可为零。

（ × ） （3）平面图形中，使静矩为零的轴必为对称轴。

（ × ） 2. 选择题（1）若截面图形有对称轴，则该图形对其对称轴的（ A ）。

A. 静矩为零，惯性矩不为零B. 静矩和惯性矩均不为零C. 静矩和惯性矩均为零D. 静矩不为零，惯性矩为零（2）设图形具有三个以上（含三个）对称轴时，对某一形心轴的惯性矩I 1 ，对某一对正交形心轴的惯性积为I 2。

则当形心轴绕形心旋转时（ A ）。

A. I 1值不变，I 2恒等于零B. I 1 值不变，I 2不恒等于零C. I 1值变化，I 2恒等于零D. I 1值变化，I 2不恒等于零（3）任意图形的面积为A ，x C 轴通过形心C ，x 1轴和x C 轴平行，并相距a ，已知图形对x 1轴的惯性矩是I 1，则对x C 轴的惯性矩为（ A ）。

A. 21xC I I Aa =-B. 0xC I =C. 21xC I I Aa =+D. 1xC I I Aa =+C x 1（4）图示等底等高的矩形和平行四边形，对其形心轴y 的惯性矩I a 和I b 满足（ A ）。

A. I a = I bB. I a > I bC. I a < I bD. 不能确定（a ）（b ）（5）设矩形对其对称轴z 的惯性矩为I ，当其长宽比保持不变，面积增加1倍时，该矩形对其对称轴z 的惯性矩将变为（ A ）。

A. 4IB. 2IC. 8ID. 16I（6）图示任意形状图形，形心轴z 将图形分为两部分，则一定成立的是（ A ）。

A. S z 1 + S z 2 = 0B. I z 1 = I z 2C. A 1 = A 2D. S z 1 = S z 2（7）图形对通过某点的所有轴的惯性矩中，图形对主惯性轴的惯性矩一定（ A ）。

材料力学(金忠谋)第六版答案-附录附录I 截面图形的几何性质I-1 求下列截面图形对z 轴的静矩与形心的位置。

解：（a ）)2)2((2)2(2h t h b t h ht t h bt s z ++=⋅++=hb h t h b h b t h t h b t A s y zc +++=+++==2)2()()2)2((22（b ）322332219211)}2)4()43()41()43(32(])4()43[(2{4442DD D D D D D D D D s z =--⨯-+⨯⨯-=ππDD D D D DAs y z c 1367.0])2()43[(2)44(219211223=-⨯+⨯==π（c ）]22)[(22)(2h t t b t h ht t t t b s z +⋅-=⨯+⨯⨯-=tb)(2)(2t b h h t t b A s y z c -++-==I-2 试求（1）图示工字形截面对形心轴 y 及 z 的惯性矩zI 与I y 。

（2）图示 T 字形截面对形心轴的惯矩zI 与I y 。

解(a)12)2)((12)2)((123333t h t b bh t h t b bh J z ---=---=12))2(2(12))(2(1222333t t h b t t t h tb J y -+=-+=(b) cmy c 643.9)520515(2)515(552522=⨯+⨯-⨯+⨯=(b433423231615121551252010186520)643.91025(12205515)5.2643.9(12515cm J cm J y z =⨯+⨯==⨯⨯--+⨯+⨯⋅-+⨯=I-3 求图示椭圆截面对长轴的惯矩、惯性半径与对形心的极惯矩。

解：θθcos ,sin ⋅=⋅=a z b yθθd b dy cos = ⎰⎰--⋅==∴b bbbz zdyy dA y J 222322223224cos sin 2cos cos sin 2ab d abd b a b J bb z πθθθθθθθππ==⋅=⎰⎰--)(4)(42422333b a ab b a ab J J J b ab ab AJ i y z p zz +=+=+====ππππI-4 试求图示的41的圆面积（半径a ）对于z ，yyy 轴的惯性积zyI 。

（此为平行移轴公式 ）
注意： •式中的a、b代表坐标值，有时可能取负值。
•等号右边各首项为相对于形心轴的量。
9
材料力学Ⅰ电子教案
2.组合截面的惯性矩和惯性积
根据惯性矩和惯性积的定义易得组合截面对于某 轴的惯性矩（或惯性积）等于其各组成部分对于同一 轴的惯性矩（或惯性积）之和：
n
Ix
i1
I
xi
n
Iy
1
材料力学Ⅰ电子教案
二、形心公式：
yc
Sz A
; zc
Sy A
.
三、组合截面的静矩：n个简单图形组成的截面，其静矩为：
n
Sz Ai yci; i 1
n
S y Ai zci; i 1
n
四、组合截面形心公式：
Ai yci
yc
i 1 n
;
Ai
i 1
例5-1 求图示T形截面形心位置。
n
Ai zci
(20010) (5 150) 2 (10 300) 0 20010 2 (10 300)
38.8 mm
由于对称知： xc=0
3
y y1 200
C O
10 150 yC x1
x
目录
材料力学Ⅰ电子教案
求图示半径为r的半圆形对其直径轴x的静矩及其形心坐标yC。
解：过圆心O作与x轴垂直的y轴，在距x任意高度y处取一个与x 轴平行的窄条，
y
d A 2 r2 y2 • d y
dA
dy
yC
所以
Sx
A
yd
A
r
0
y( 2
r2 y2 )d y 2 r3 3
Cr
y

2
267 104 mm4
附录I 截面的几何性质
于是有组合截面对于两主轴x轴和y轴的惯性矩分别为
I x I x1 2 I x2 3690 10 4 mm 4 2 2110 10 4 mm 4 7910 10 4 mm 4 I y I y1 2 I y2 431 10 4 mm 4 2 267 10 4 mm 4 965 10 4 mm 4
附录I 截面的几何性质
解：将原平面图形分成上中下三个矩形。过形心建立参考坐标 系
40 53 5 603 I x 2I x1 I x2 2 40 5 27.52 12 12 y 4 4 393333 mm 39.33cm I y 2 I y1 I y2
I yC 218.415 cm 形心位置如图所示 90 mm×90 mm×12 mm 等边角钢截面
4
A 20.30 cm 2 I xC I yC 149.22 cm 4
形心位置如图所示
附录I 截面的几何性质
组合截面的形心C在对 称轴x上。以两个角钢截面的 形心连线为参考轴,只需求组 合截面形心C以该轴为基准 的横坐标 x ：
a
x
附录I 截面的几何性质
例题
图示组合截面由一个 25c号槽钢截面和两个 90 mm×90 mm×12 mm等边角钢截面组成。 试求此截面分别对于形 心轴x和y的惯性矩Ix 和 Iy 。
附录I 截面的几何性质
解: 1. 求组合截面的形心位置
由型钢规格表查得：25c号槽钢截面 A 44.91cm 2， I xC 3 690.45 cm4
I x1 y1 dA
2 A
x1 x cos y sin y1 x sin y cos

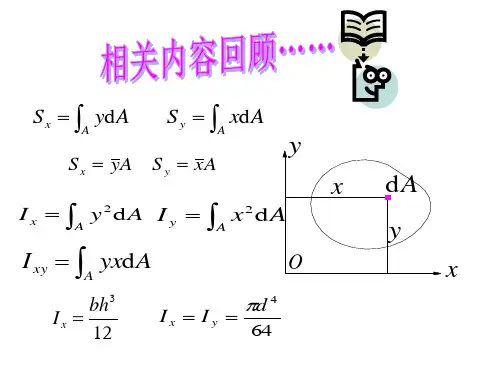
第五节截面图形的几何性质一、静矩与形心对图所示截面静矩的量纲为长度的三次方。

对于由几个简单图形组成的组合截面形心坐标显然，若z轴过形心，y c=0，则有S z=0，反之亦然：若y轴过形心，z c=0，则有S y=0，反之亦然。

【真题解析】5—30（2007年真题）图所示矩形截面，m-m线以上部分和以下部分对形心轴z的两个静矩( )。

(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(c)绝对值不等，正负号相同(D)绝对值不等，正负号不同解：根据静矩定义，图示矩形截面的静矩等于m-m线以上部分和以下部分静矩之和，即，又由于z轴是形心轴，Sz=0，故答案：(B)二、惯性矩、惯性半径、极惯性矩、惯性积对图所示截面，对z轴和y轴的惯性矩为惯性矩总是正值，其量纲为长度的四次方，也可写成i z、i y称为截面对z、y轴的惯性半径，其量纲为长度的一次方。

截面对0点的极惯性矩为因=y2+z2，故有I p=I z+I y，显然I p也恒为正值，其量纲为长度的四次方。

截面对y、z轴的惯性积为I yz可以为正值，也可以为负值，也可以是零，其量纲为长度的四次方。

若y、z两坐标轴中有一个为截面的对称轴，则其惯性积I yz恒等于零。

例6图(a)、(b)所示的两截面，其惯性矩关系应为哪一种？A.(I y)1>(I y)2,(I z)1=(I z)2B. (I y)1=(I y)2, (I z)1>(I z)2C.(I y)1=(I y)2,(I z)1<(I z)2D. (I y)1<(I y)2,(I z)1=(I z)2解：两截面面积相同，但图 (a)截面分布离z轴较远，故I z较大。

对y轴惯性矩相同。

答案：B2016—63真题面积相同的两个如图所示，对各自水平形心轴 z 的惯性矩之间的关系为（）。

提示：图（ a ）与图（ b ）面积相同，面积分布的位置到 z 轴的距离也相同，故惯性矩I za=I zb而图（ c ）虽然面积与（ a ）、（ b ）相同，但是其面积分布的位置到 z 轴的距离小，所以惯性矩I zc也小。

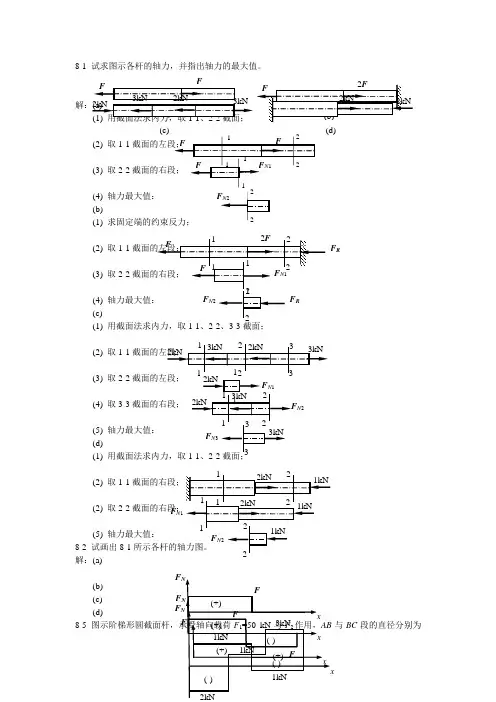
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

《工程力学2习题解答》建筑1001班陈飞力学教研室编著1-2. 试求图示结构mm 和nn 两截面上的内力，并指出AB 和BC 两杆属何种基本变形。

解：（1）求约束反力：取杆AB 为研究对象∑∑∑=⨯-⨯==-+===0233 003 000BCABCAAN M N Y Y X X 解得：kN Y kN N A BC 1 2==（2）求m-m 截面内力：将杆AB 沿截面m-m 截开, 取左半部分kNm Y M kN Y Q A m-m A m m 11 1=⨯===-AB 杆发生弯曲变形。

（3）求n-n 截面内力：取杆BC 为研究对象，截开n-n 截面kN N N BC n n 2==-BC 杆发生拉伸变形1-3. 拉伸试件A 、B 两点的距离l 称为标距，在拉力作用下，用引伸仪量出两点距离的增量为Δl =5×10-2mm 。

若l 的原长为l =10cm ，试求A 、B 两点间的平均应变。

解：平均应变为42105100105Δ--⨯=⨯==l l m ε1-4. 图示三角形薄板因受外力而变形。

角点B 垂直向上的位移为0.03mm ，但AB和BC 仍保持为直线。

试求沿OB 的平均应变，并求AB 、BC 两边在B 点夹角的变化。

解：（1） 求OB 方向的平均线应变n4105.212003.0Δ120-⨯=====l l mmOA OB m ε （2）求AB 与BC 两边的角应变4105.2'22-⨯=-=OB AO arctg πγ2-1. 试求图示各杆1-1、2-2、3-3截面的轴力， 并作轴力图。

解: (a)（1）求约束反力kNR R X 500203040 0==-++-=∑（2）求截面1-1的轴力kNN NR X 500011==+-=∑（3）求截面2-2的轴力kNN NR X 10040 022==++-=∑（4）求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑（5）画轴力图(b)（1）求截面1-1的轴力01=N（2）求截面2-2的轴力 PN4022==（3）求截面3-3的轴力PN P P NX 304 033==-+=∑（4）画轴力图2-2. 作用图示零件上的拉力P=38kN ，试问零件内最大拉应力发生于哪个横截面上？并求其值。

三、平行移轴公式
1、平行移轴公式
右图任意截面，zc、yc 轴为通过截面形心C的一对正交轴，z、y轴为分别与zc、yc 轴平行的轴，
两平行轴之间的距离分别为a和b。
根据定义，图形对zc、yc 轴的惯性矩和惯性积分别为
Izc yc2dA, I yc zc2dA, Izc yc yc zcdA
I zy
i 1
I yzi
Izi， Iyi
,Iyz i
----指第
i个简单截面对
y, z
轴的惯性矩，惯性积。
例题 求T形截面对其形心轴 zC 的惯性矩（单位为mm）。
解：将截面分成两个矩形截面。 截面的形心必在对称轴 y 上。
取过矩形2的形心且平行于底边的轴作为参考轴记作z轴。
A1
20140
2800mm2 ,
Iz c
I1 zc
I2 zc
7.68106
4.43106
12.11106 mm4
20 140
yc
20
1
a1 zc
y1 a2 yc z
2
100
a2A b2A
c
I zy I zc yc abA
上式即为惯性矩和惯性积的平行移轴公式。
y
z yc
b
zc
dA
C
yc
a y zc
O
z
2、组合截面的惯性矩、惯性积
组合截面对某轴的惯性矩、惯性积，等于各简单图形对此轴的惯性矩、惯性积的代数和。
n
Iz Iz i
i 1
n
I y I y
i1 i
n
ycdA a2
dA
A
A
A
A
A
A

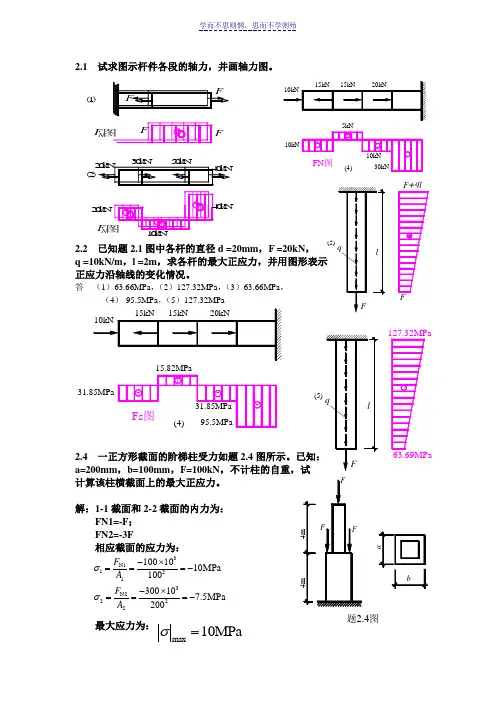
2.1 试求图示杆件各段的轴力，并画轴力图。

2.2 已知题2.1图中各杆的直径d =20mm ，F =20kN ，q =10kN/m ，l =2m ，求各杆的最大正应力，并用图形表示 正应力沿轴线的变化情况。

答 （1）63.66MPa ，（2）127.32MPa ，（3）63.66MPa ，（4）-95.5MPa ，（5）127.32MPa2.4 一正方形截面的阶梯柱受力如题2.4图所示。

已知：a=200mm ，b=100mm ，F=100kN ，不计柱的自重，试 计算该柱横截面上的最大正应力。

解：1-1截面和2-2截面的内力为： FN1=-F ；FN2=-3F相应截面的应力为：最大应力为：15kN15kN20kN10kN(4)10kN5kN10kN 30kN+---FN 图-+++FF FF 20k N 30k N 50k N 40k N 40k N10k N 20k N (2)(1)F N图图NF l(5)q FFF q ll(5)qF+127.32MPa63.69MPa15kN 15kN 20kN 10kN (4)31.85MPa 15.82MPa +---Fs 图31.85MPa95.5MPa 4m4mabF题2.4图FF3N11213N22221001010MPa 100300107.5MPa200F A F A σσ-⨯===--⨯===-max 10MPaσ=2.6 钢杆受轴向外力如图所示，横截面面积为500mm2，试求 ab 斜截面上的应力。

解： FN=20kN2.8 图示钢杆的横截面积 A=1000mm2，材料的弹性模量E=200GPa ，试求：（1）各段的轴向变形；（2）各段的轴向线应变；（3）杆的总伸长。

解：轴力图如图所示2.10 图示结构中，五根杆的抗拉刚度均为EA ，杆AB 长为l ，ABCD 是正方形。

在小变形条件下，试求两种加载情况下，AB 杆的伸长。

解 （a ）受力分析如图，由C 点平衡可知：3020kNob aa b a b p αs αατF N o N N 0cos30==F F p A A ααo 2oN 03cos30cos 302010330MPa 5004F p A σ==⨯=⨯=αα3o o o N020103sin30cos30sin3017.32MPa 5004F p A ⨯===⨯=αατ-+20kN20kN 20kN ⅠⅡⅢ20kN20kN1m 1m 2m12320N 0N 20N N N N F k F k F k ===-41119624333962011020010100010020221020010100010N N F l L m EA L m F l L m EA ----⨯∆===⨯⨯⨯∆=⨯∆===-⨯⨯⨯⨯4411122244333101010210102L m l mL l L ml mεεε----∆===∆==∆-⨯===-41243100210L m L m L m--∆=∆=∆=-⨯I II III 0.1mm 00.2mm 0.1mm l l l l ∆=∆+∆+∆=+-=-F ’AC=F ’CB=0；由D 点平衡可知： F ’AD=F ’BD=0； 再由A 点的平衡：因此（b ）受力分析如图，由C 点平衡可知：再由A 点的平衡：因此2.12 图示结构中，水平刚杆AB 不变形，杆①为钢杆，直径d1=20mm ，弹性模量E1=200GPa ；杆②为铜杆，直径d2=25mm ，弹性模量E2=100GPa 。

附录 I 截面图形的几何性质
附录Ⅰ 截面图形的几何性质
I-1 填空题： I-1(1) 当一个正方形的边长和一个圆形的直径相等时，两图形对 其形心轴的惯性矩之比应为 16 。
3π
I-1(2) 若已知图示平面图形对 A 轴的惯性矩为 27 bh3 ，则图 4
形对 C 轴的惯性矩为 3 bh3 ，对 D 轴的惯性矩为 9 bh3 。
y xC
−α
0
α
= 2 R3 sin α 。 3
x Oα C
R
A = R 2α 。
xC
=
2R3 sin α 3R 2α
=
2 R sinα 3α
。
题 I-4 图
I-5 如图的截面由一个直径为 D 的半圆和一个矩形组成。如果图形的形心位于半圆的水
平直径处，求矩形的高 a。
解：上半圆对形心轴的静矩：
S1
=
12
-1-
B
A
题 I-1(6) 图
工程力学习题解答
I-2 单选题：
I-2(1) 边长为 4a 的正方形，在如图位置挖去一个边长为 a
的小正方形，余下的阴影图形对坐标轴 x、y、x′、y′的静
矩分别为 S x , S y , S x′ , S y′ ，其中只有 C 是对的。
A． S x
=
a3 2
B． S y =
C． I x = I x′ + (a2 + a′2 ) A D． I x = I xC + (a + a′)2 A E． I x = I x′ + 2aa′A + a2 A F． I x = I x′ + 2aSx′ + a2 A
b′ C a′

O1 O 2
O
x
O3
x 1
C
课堂练习
I.
&
任意图形，若对某一对正交坐标轴的惯性积为零， 则这一对坐标轴一定是该图形的（ ）。
B
A. 形心轴； B. 主轴 C. 主形心轴 D. 对称轴 在图示开口薄壁截面图形中，当（ 为一对主轴。
y
）时，y-z轴始终保持
A. y轴不动，x轴平移； B. x轴不动，y轴平移； C. x轴不动，y轴任意移动；
y b C 1x C 2x O a x
æ 1 öæ 2 ö æ 1 öæ h ö = ç bh ÷ç h ÷ + ç ah ÷ç ÷ è 2 øè 3 ø è 2 øè 3 ø
h 2 = (a + 2 b ) 6
形心位置
h
x = 0
h 2 (a + 2 b ) h a + 2 b S x y = = பைடு நூலகம்· = 6 A h 3 a + b (a + b ) 2
主惯性矩:
图形对主轴的惯性矩,称主惯性矩
形心主轴:
过形心的主轴称为形心主轴
形心主矩:
图形对形心主轴的惯性矩称为形心主矩
课堂练习
I.
&
在下列关于平面图形的结论中，（
）是错误的。
A.图形的对称轴必定通过形心； B.图形两个对称轴的交点必为形心； C.图形对对称轴的静矩为零； D.使静矩为零的轴必为对称轴。 在平面图形的几何性质中，（
y
dA y
ü2、惯性矩和极惯矩永远为正，
惯性积可能为正、为负、为零。
x 1
ü3、任何平面图形对于通过其形

5-1. 矩形截面悬臂梁如图所示，已知l =4m ，h/b=2/3，q=10kN/m ，[σ]=10MPa ，试确定此梁横截面的尺寸。

解：（1）画梁的弯矩图由弯矩图知：22max ql M =（2）计算抗弯截面模量96326332h hbh W ===（3）强度计算mmb mm ql h h ql h ql WM 277416][29][12992323232maxmax ≥=≥∴≤⋅===σσσ5-2. 20a 工字钢梁的支承和受力情况如图所示，若[σ]=160MPa ，试求许可载荷。

解：（1）画梁的弯矩图qNo20aql 2x由弯矩图知：32max P M =（2）查表得抗弯截面模量3610237m W -⨯=（3）强度计算kNW P P WW PW M 88.562][3][3232max max =≤∴≤⋅===σσσ 取许可载荷kN P 57][=5-3. 图示圆轴的外伸部分系空心轴。

试作轴弯矩图，并求轴内最大正应力。

解：（1）画梁的弯矩图由弯矩图知：可能危险截面是C 和B 截面 （2）计算危险截面上的最大正应力值x1.34kNmxC 截面：MPa d MW M CC C C C 2.63323max ===πσ B 截面：MPa D d D M W M BB BBB B B 1.62)1(32443max =-==πσ （3）轴内的最大正应力值MPaC 2.63max max ==σσ5-8. 压板的尺寸和载荷如图所示。

材料为45钢，σs =380MPa ，取安全系数n=1.5。

试校核压板的强度。

解：（1）画梁的弯矩图由弯矩图知：危险截面是A 截面，截面弯矩是Nm M A 308=（2）计算抗弯截面模量3633210568.1)1(6m Hh bH W -⨯=-=（3）强度计算许用应力A-AxMPa nS253][==σσ强度校核][196max σσ MPa WM A==压板强度足够。

附录I 截面的几何性质 习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。

（a ）解：)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=（b ）解：)(42250265)6520(3mm y A S c x =⨯⨯=⋅= （c ）解：)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=（d ）解：)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩，并确定其形心的坐标。

解：用两条半径线和两个同心圆截出一微分面积如图所示。

dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的静矩为： θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为：32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=，所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。

（a ） 解：习题I-3(a): 求门形截面的形心位置矩形 Li Bi Ai Yci AiYci Yc 离顶边上 400 20 8000 160 1280000 左 150 20 3000 75 225000 右150 20 3000 75 225000140001730000Ai=Li*Bi Yc=∑AiYci/∑Ai(b)解：(c)解：[习题I-4]试求图示四分之一圆形截面对于x轴和y轴的惯性矩x I、y I和惯性积xy I。

解：用两条半径线和两个同心圆截出一微分面积如图所示。

dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的惯性矩为： θθθθθdxd x dx xd x dx xd y dA y dI x ⋅=⋅⋅=⋅==232222sin sin )(四分之一圆对x 轴的惯性矩为： ⎰⎰⎰-⋅==2/0042/02322cos 1]4[sin ππθθθθd x d dx x I r rx)]2(2cos 21[2142/02/04θθθππd d r ⎰⎰-⋅= }]2[sin 212{82/04πθπ-=r 164r ⋅=π由圆的对称性可知，四分之一圆对y 轴的惯性矩为：164r I I x y ⋅==π微分面积对x 轴、y 轴的惯性积为：xydA dI xy =8)42(21]42[21)(21444042222022r r r x x r dx x r x ydx xdx I r rx r rxy =-=-=-==⎰⎰⎰- [习题I-5] 图示直径为mm d 200=的圆形截面，在其上、下对称地切去两个高为mm 20=δ的弓形，试用积分法求余下阴影部分对其对称轴x 的惯性矩。

(Ai 和xi , yi分别为第i个简单图形的面积及其形心坐标）
5. 组合截面的形心坐标公式
n
将 S y Ai xi i1
n
S x Ai yi i1
代入 S y A x Sx A y
解得组合截面的形心坐标公式为：
n
Ai xi
x
i 1 n
Ai
i 1
n
Ai yi
y
i 1 n
Ai
i 1
（注：被“减去”部分图形的面积应代入负值）
例 试计算图示三角形截面对x轴的静矩。
y
dy
h
b(y)
y
O
b
x
解：取平行于x轴的狭长条，易求 b( y) b (h y)
因此 d A b (h y) d y
ห้องสมุดไป่ตู้
h
所以对x轴的静矩为
h hb
bh2
S x
y d A (h y)y d y
A
0h
6
2
4
I2 xc yc
x
I x1 A y12 d A
y
Ix1
cos2
y2 d A sin2
A
x2 d A
A
2sin cos A xy d A
I x cos2 I y sin2 2I xy sin cos
利用二倍角函数代入上式，得转轴公式 ：
I x1
Ix
2
Iy
Ix
Iy 2
cos2
I xy sin 2
n
Ix
i1
I
xi
n
Iy
i1
I
yi
n
I xy I i1 xyi

yC
Sz A
558000 9000
62
Sz Sz1 Sz2 120 40 20 140 30110 558000
A A1 A2 120 40 140 30 9000
120
I
CI
C
CII
II
y 30
参考轴
z 40
yC
zC 140
注意
① 由两块组成组合图形，其复合图形形心一定位于两个子图的形心连线上。 ② 组合图形形心计算公式也适用于负面积情况， 但要记住面积为负号。
z
I
C1 C
s
C2
II
b
y1 h
y
y2
t
典型例题
例3 已知组合截面尺寸t=20mm，h=140mm，b=100mm。试求截面图
形对形心轴 y 的惯性矩。
t
解： 由平行移轴定理
矩形1对y轴的惯性矩：
I (1) y
I y1
b12 A1
矩形2对y轴的惯性矩：
I (2) y
I y2
b22 A2
整个截面的惯性矩：
Iz
y 2 dA
A
h y2bdy 0
b
y3 3
/
h 0
bh3 3
y
h b
dy y
z
典型例题
例2 试求图示截面对形心轴zC轴的惯性矩。
IzC
y 2 dA
A
h
2 h
y2bdy
2
b
y3 3
h
/
2
h
2
bh3
12
I yC
z 2dA
A
y
yC
hb3 =

北京交通大学材料力学答案 北交《材料力学》在线作业一 一,单选题 1.均匀性假设认为，材料内部各点的是相同的。

A.应力 B.应变 C.位移 D.力学性质 ? 正确答案：D 2.各向同性认为，材料沿各个方向具有相同的。

A.力学性质 B.外力 C.变形 D.位移 ? 正确答案：A 3.材经过冷作硬化以后，基本不变。

A.弹性模量 B.比例极限 C.延伸率 D.断面收缩率 ? 正确答案：A 4.拉杆的应力计算公式σ=N/A的应用条件是：。

A.应力在比例极限内 B.外力的合力作用线必须沿杆件的轴线 ? 正确答案：B 5.外力包括: A.集中力和均布力 B.静载荷和动载荷 C.所有作用在物体外部的力 D.载荷与支反力 ? 正确答案：D 6.在静不定桁架中，温度均匀变化会： A.引起应力，不引起变形 北交《材料力学》在线作业一 一、单选题 1.低碳钢圆截面在拉伸破坏时，标距由100毫米变成130毫米。

直径由10毫米变为7毫米，则Poisson’srtio(泊松比)ε为： .μ=(10-7)/(130-100)= .μ=ε’/ε=-/=-1 .μ=|ε’/ε|=1 .以上答案都错 正确答案： 2.关于铸铁正确的是 .抗剪能力比抗拉能力差 .压缩强度比拉伸强度高 .抗剪能力比抗压能力高 正确答案： 3.根据小变形条件，可以认为 .构件不变形 .构件不破坏 .构件仅发生弹性变形 .构件的变形远小于原始尺寸 正确答案： 4.用截面法求内力时，是对建立平衡方程而求解的。

.截面左段 .截面右段 .左段或右段 .整个杆件 正确答案： 5.材经过冷作硬化以后，基本不变。

.弹性模量 .比例极限 .延伸率 .断面收缩率 正确答案： 6.在静不定桁架中，温度均匀变化会： .引起应力，不引起变形 .引起变形，不引起应力； .同时引起应力和变形 .不引起应力和变形 正确答案： 7.均匀性假设认为，材料内部各点的是相同的。

.应力 .应变 .位移 .力学性质 正确答案： 8.钢材进入屈服阶段后，表面会沿出现滑移线。

附录 截面图形的几何性质一、是非判断题⒈ 图形对某一轴的静矩为零，则该轴必定通过图形的形心。

（ √ ）⒉ 图形在任一点只有一对主惯性轴。

（ × ）⒊ 有一定面积的图形对任一轴的轴惯性矩必不为零。

（ √ ）⒋ 图形对过某一点的主轴的惯性矩为图形对过该点所有轴的惯性矩中的极值。

（ √ ）二、填空题⒈ 组合图形对某一轴的静矩等于 各组成图形对同一轴静矩 的代数和。

⒉ 图形对任意一对正交轴的惯性矩之和，恒等于图形对 两轴交点的极惯性矩 。

⒊ 如果一对正交轴中有一根是图形的对称轴，则这一对轴为图形 主惯性轴 。

⒋ 过图形的形心且 图形对其惯性积等于零 的一对轴为图形的形心主惯性轴。

三、选择题⒈ 图形对于其对称轴的（ A ）A 静矩为零，惯性矩不为零；B 静矩和惯性矩均为零C 静矩不为零，惯性矩为零；D 静矩和惯性矩均不为零⒉ 直径为d 的圆形对其形心主轴的惯性半径=（ C ）。

i A d/2 B d/3 C d/4 D d/8⒊ 图示截面图形中阴影部分对形心主轴的惯性矩=（ C ）。

z Z I A B123234dD D -π63234dD D -π C D 126434dD D -π66434dD D -πz四、计算题1、求图示平面图形中阴影部分对z 轴的静矩。

232.0)2.06.0(4.0bh h h h b S Z =+⋅⋅=()8842422222bh h H B h h b h H h h H B S Z +-=⋅⋅+⎪⎭⎫ ⎝⎛-+⋅-⋅=2、求图示平面图形对z 、y 轴的惯性矩。

4523231023.251040121040251040123010mm I I I II I Z ⨯=⋅⋅+⋅+⋅⋅+⋅=+=由于图形对称，451023.2mm I I Z Y ⨯===3、试求图示平面图形的形心主惯性轴的位置，并求形心主惯性矩。

mm y C 7.5610020201401010020902010=⋅+⋅⋅⋅+⋅⋅=4723231021.17.46200.1012201003.33201401214020mm I I I II I Z ⨯=⋅⋅+⋅+⋅⋅+⋅=+=46331076.112100201220140mm I Y ⨯=⋅+⋅=z zz。