二年级奥数.计算.数阵图 (2)

1. 瞭解數陣圖的種類2. 學會一些解決數陣圖的解題方法3. 能夠解決和數論相關的數陣圖問題.一、數陣圖定義及分類：1. 定義：把一些數字按照一定的要求，排成各種各樣的圖形，這類問題叫數陣圖.2. 數陣是一種由幻方演變而來的數字圖.數陣圖的種類繁多，這裏只向大家介紹三種數陣圖：即封閉型數陣圖、輻射型數陣圖和複合型數陣圖.3.二、解題方法：解決數陣類問題可以採取從局部到整體再到局部的方法入手： 第一步：區分數陣圖中的普通點(或方格)和關鍵點(或方格)；第二步：在數陣圖的少數關鍵點(一般是交叉點)上設置未知數，計算這些關鍵點與相關點的數量關係，得到關鍵點上所填數的範圍；第三步：運用已經得到的資訊進行嘗試．這個步驟並不是對所有數陣題都適用，很多數陣題更需要對數學方法的綜合運用．複合型數陣圖【例 1】 由數字1、2、3組成的不同的兩位數共有9個，老師將這9個數寫在一個九宮格上，讓同學選數，每個同學可以從中選5個數來求和．小剛選的5個數的和是120，小明選的5個數的和是111．如果兩人選的數中只有一個是相同的，那麼這個數是_____________．例題精講知識點撥教學目標5-1-3-2.數陣圖313233212223131211【考點】複合型數陣圖 【難度】3星 【題型】填空 【關鍵字】迎春杯，中年級，決賽，3題【分析】 這9個數的和：111213212223313233++++++++10203031233198=++⨯+++⨯=（）（）由小剛和小明選的數中只有一個是相同的，可知他們正好把這9個數全部都取到了，且有一個數取了兩遍．所以他們取的數的總和比這9個數的和多出來的部分就是所求的數．那麼，這個數是12011119833+-=．【答案】33【例 2】 如圖1，圓圈內分別填有1，2，……，7這7個數。

如果6個三角形的頂點處圓圈內的數字的和是64，那麼，中間圓圈內填入的數是 。

【考點】複合型數陣圖 【難度】3星 【題型】填空 【關鍵字】希望杯，五年級，復賽，第5題，5分【解析】 2【答案】2【例 3】 如下圖（1）所示，在每個小圓圈內填上一個數，使得每一條直線上的三個數的和都等於大圓圈上三個數的和.（1）17894【考點】複合型數陣圖 【難度】3星 【題型】填空【解析】 為敘述方便，先在每個圓圈內標上字母，如圖（2），（2）a cb49817則有a+4+9=a+b+c （1）b+8+9=a+b+c （2）c+17+9=a+b+c （3）（1）+（2）+（3）：（a+b+c ）+56=3（a+b+c ），a+b+c=28，則 a=28－（4+9）=15，b=28－（8+9）=11，c=28-（17+9）=2解：見圖.1789411215【答案】1789411215【例 4】 請你將數字1、2、3、4、5、6、7填在下面圖（1）所示的圓圈內，使得每個圓圈上的三個數之和與每條直線上的三個數之和相等.應怎樣填？【考點】複合型數陣圖 【難度】3星 【題型】填空【解析】 為了敘述方便，將各圓圈內先填上字母，如圖（2）所示.設A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k （A+B+C ）+（A+F+G ）+（A+D+E ）+（B+D+F ）+（C+E+G ）=5k ，3A+2B+2C+2D+2E+2F+2G=5k ，2（A+B+C+D+E+F+G ）+A=5k ，2（1+2+3+4+5+6+7）+A=5k ，56+A=5k.，因為56+A 為5的倍數，得A=4，進而推出k=12，因為在1、2、3、5、6、7中，1+5+6=7+3+2=12，不妨設B=1，F=5，D=6，則C=12-（4+1）=7，G=12-（4+5）=3，E=12-（4+6）=2.，解：得到一個基本解為：（見圖）7654321【答案】7654321【例 5】 在左下圖的每個圓圈中填上一個數，各數互不相等，每個圓圈有3個相鄰(即有線段相連的圓圈)的圓圈。

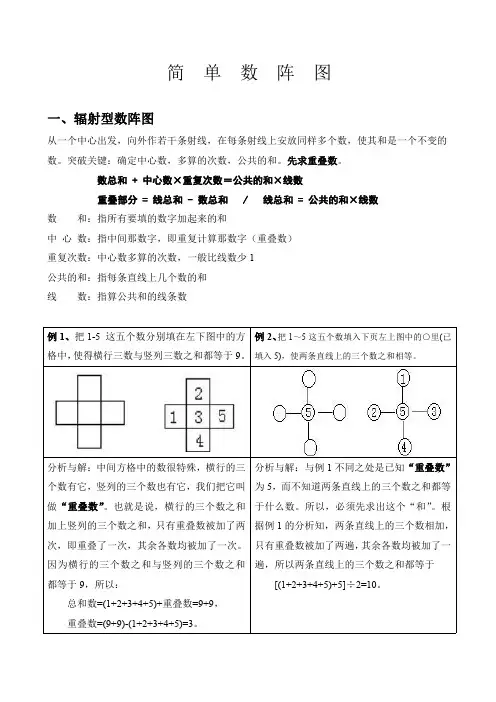
简单数阵图一、辐射型数阵图从一个中心出发，向外作若干条射线，在每条射线上安放同样多个数，使其和是一个不变的数。

突破关键：确定中心数，多算的次数，公共的和。

先求重叠数。

数总和+中心数×重复次数＝公共的和×线数重叠部分=线总和-数总和/线总和=公共的和×线数数和：指所有要填的数字加起来的和中心数：指中间那数字，即重复计算那数字（重叠数）重复次数：中心数多算的次数，一般比线数少1公共的和：指每条直线上几个数的和线数：指算公共和的线条数例1、把1-5这五个数分别填在左下图中的方格中，使得横行三数与竖列三数之和都等于9。

例2、把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。

分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于9，所以：总和数=(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。

分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。

所以，必须先求出这个“和”。

根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。

例3、把1~5这五个数填入右图中的○里，使每条直线上的三个数之和相等例4、将1~7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于10。

分析与解：例1是知道每条直线上的三数之和，不知道重叠数；例2是知道重叠数，不知道两条直线上的三个数之和；本例是这两样什么都不知道。

但由例1、例2的分析知道，(1+2+3+4+5)+重叠数=每条直线三数之和×2，每条直线上三数之和=(15+重叠数)÷2。

数阵图
小朋友们，你喜欢填数字游戏吗？要想准确的填出图中的每一个数，可不是一
件容易的事，这就要我们小朋友们认真去观察图，观察数字的排列规律，这样才能
找到填图的方法.下面我们就一起来学习吧！
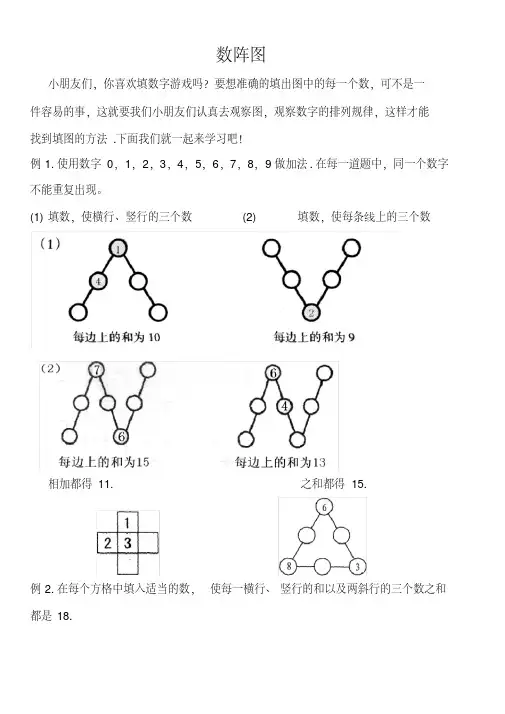
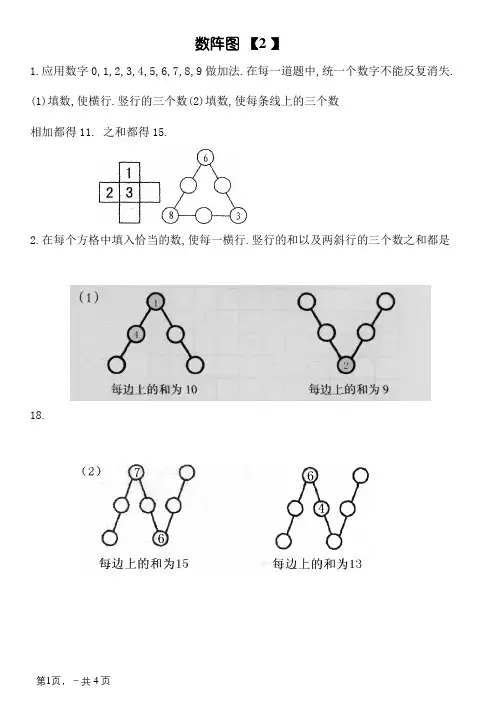
例1.使用数字0，1，2，3，4，5，6，7，8，9做加法.在每一道题中，同一个数字不能重复出现。

(1)填数，使横行、竖行的三个数 (2)填数，使每条线上的三个数
相加都得11. 之和都得15.
例2.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.
在空格中填入适当的数，使横行和竖行或每条对角线上的三个数相加都等于15。

例3.把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数之
和都等于14。

拓展练习
（1）把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等
于12。

（2）把1，2，3，4，5，7分别填入○里，使每一个大椭圆上的四个数之和等于13.
例4.把1，2，3，4，5，6，7这七个数分别填入○里，使每条直线上的三个数相加的和都为12。

把1，3，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为17。

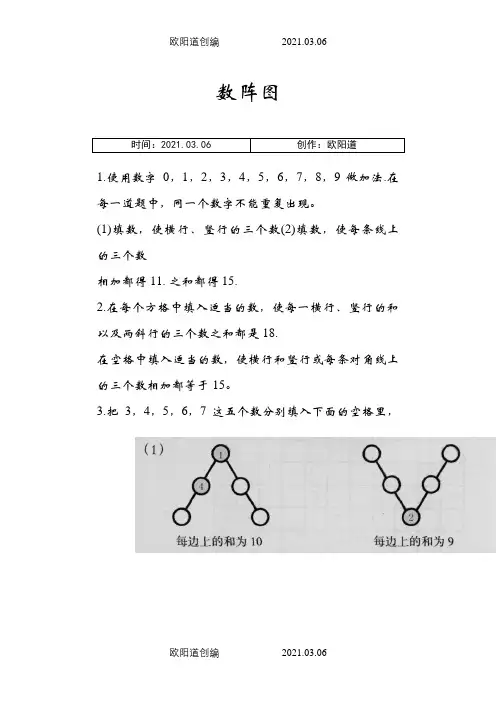
数阵图时间：2021.03.06 创作：欧阳道1.使用数字0，1，2，3，4，5，6，7，8，9做加法.在每一道题中，同一个数字不能重复出现。

(1)填数，使横行、竖行的三个数(2)填数，使每条线上的三个数相加都得11. 之和都得15.2.在每个方格中填入适当的数，使每一横行、竖行的和以及两斜行的三个数之和都是18.在空格中填入适当的数，使横行和竖行或每条对角线上的三个数相加都等于15。

3.把3，4，5，6，7这五个数分别填入下面的空格里，使横行、竖行的三个数之和都等于14。

拓展练习（1）把2，3，4，5，6这五个数分别填入圆圈中，使每条线上三个数相加的和都等于12。

（2）把1，2，3，4，5，6分别填入○里，使每一个大椭圆上的四个数之和等于13.例 4.把1，3，5，7，9，11，13这七个数分别填入○里，使每条直线上的三个数相加的和都为17。

简单数阵图例1、把1—5 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。

例2、把1—7这七个数分别填入图中的各○内，使每条线段上三个○内数的和等于10。

例3、在下图圆圈内分别填入数字1~9，使两条直线上五个数的和相等，和是多少？例4、把1～6这六个数分别填在下图中三角形三条边的六个○内，使每条边上三个○内数的和等于9。

例5、将2—9这八个数分别填入右图的○里，使每条边上的三个数之和都等于18。

例6、将1、2、3、4、5、6、7、8、9九个数字分别填入图中的小圆圈中，使三角形每边上四个数的和是17。

1、把2—6 这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于13。

2、在图中填入2—9，使每边3个数的和等于15。

3、将数字1—9分别填在图中的○内使每条线上五个○内数的和等于27。

4、把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条线上三个数的和等于30。

第四讲有趣的数阵图经典精讲:数阵图: 将一些数按照一定的要求排列成各种各样的图形。

数阵图是一种趣味性很强的填数游戏, 它的形式多样, 绚丽奇妙。

这里给同学们介绍三种形式的数阵图, 即封闭型数阵图、辐射型数阵图和复合型数阵图。

（一）辐射型数阵图（像雪花）从一个中心出发, 向外作若干条射线, 在每条射线上安放同样多个数, 使其和是一个不变的数。

突破关键：确定中间数, 多算的次数, 公共的和线数x公共的和=数和+中心数x重复次数【例1】把1—5 这五个数分别填在左下图中的方格中, 使得横行三数之和与竖列三数之和都等于9。

【例2】把1—7这七个数分别填入图1中的各○内, 使每条线段上三个○内数的和相等。

【课堂练习】将1～11这11个数分别填入图11中的方格内, 每个数只许用一次, 使相邻两个或三个方格内数的和都相等。

（二）封闭型数阵图（像围墙）多边形的每条边放同样多的数, 使它们的和都等于一个不变的数。

突破关键：确定顶点上的数字, 公共的和边数x公和=数和+重叠数和【例3】把1～6这六个数分别填在下图中三角形三条边的六个○内, 使每条边上三个○内数的和相等。

（本题有24种填法, 你能想出几种？）【例4】将2—9这八个数分别填入右图的○里, 使每条边上的三个数之和都等于18。

【课堂练习】1.1—10这十个数, 分别填在图9中五边形五条边上的十个○内, 并使五条边上的三个○内数的和相等。

2.把1—8这8个数, 填入图13中的八个○内, 使每条线段上的四个数的和, 与每个四边形四个顶点上的四个数的和都相等。

（三）复合型数阵图既有辐射型数阵图的特点, 又有封闭型数阵图的特点。

突破点: 找出关键位置重复次数。

【例5】将1～7这七个数分别填入下图的○里, 使得每条直线上三个数之和与每个圆圈上的三个数之和都相等。

【课堂练习】1.将1.2.3.4.5.6六个数字填入图中的小圆圈内, 使每个大圆上四个数字的和是16。

2. 将1—8这八个数, 分别填入图10中两个圆圈的八个○内, 使每个圆圈上五个○内数的和分别为20、21.22。

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手： 第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个，老师将这9个数写在一个九宫格上，让同学选数，每个同学可以从中选5个数来求和．小刚选的5个数的和是120，小明选的5个数的和是111．如果两人选的数中只有一个是相同的，那么这个数是_____________．313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯，中年级，决赛，3题 【分析】 这9个数的和：111213212223313233++++++++10203031233198=++⨯+++⨯=（）（）由小刚和小明选的数中只有一个是相同的，可知他们正好把这9个数全部都取到了，且有一个数取了两遍．所以他们取的数的总和比这9个数的和多出来的部分就是所求的数．那么，这个数是12011119833+-=．【答案】33【例 2】 如图1，圆圈内分别填有1，2，……，7这7个数。

如果6个三角形的顶点处圆圈内的数字的和是64，那么，中间圆圈内填入的数是 。

例题精讲知识点拨教学目标5-1-3-2.数阵图【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】希望杯，五年级，复赛，第5题，5分 【解析】 2 【答案】2【例 3】 如下图（1）所示，在每个小圆圈内填上一个数，使得每一条直线上的三个数的和都等于大圆圈上三个数的和.（1）17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便，先在每个圆圈内标上字母，如图（2），（2）a cb49817则有a+4+9=a+b+c （1）b+8+9=a+b+c （2）c+17+9=a+b+c （3） （1）+（2）+（3）：（a+b+c ）+56=3（a+b+c ），a+b+c=28，则 a=28－（4+9）=15，b=28－（8+9）=11，c=28-（17+9）=2解：见图.1789411215【答案】1789411215【例 4】 请你将数字1、2、3、4、5、6、7填在下面图（1）所示的圆圈内，使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填？【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为了叙述方便，将各圆圈内先填上字母，如图（2）所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k（A+B+C ）+（A+F+G ）+（A+D+E ）+（B+D+F ）+（C+E+G ）=5k ，3A+2B+2C+2D+2E+2F+2G=5k ，2（A+B+C+D+E+F+G）+A=5k，2（1+2+3+4+5+6+7）+A=5k，56+A=5k.，因为56+A为5的倍数，得A=4，进而推出k=12，因为在1、2、3、5、6、7中，1+5+6=7+3+2=12，不妨设B=1，F=5，D=6，则C=12-（4+1）=7，G=12-（4+5）=3，E=12-（4+6）=2.，解：得到一个基本解为：（见图）7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数，各数互不相等，每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。

小学奥数之数阵图解题方法1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手： 第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．模块一、封闭型数阵图【例 1】 把1～8的数填到下图中，使每个四边形中顶点的数字和相等。

【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯，3年级，第6题 【解析】5-1-3-1.数阵图教学目标知识点拨例题精讲【答案】【例 2】 将1～8这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于14，且数字1出现在四边形的一个顶点上.应如何填？【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便，先在各圆圈内填上字母，如下图（2）.由条件得出以下四个算式：a+b+c=14（1） c+d+e=14 （2） e+f+g=14 （3）a+h+g=14 （4）由（1）+（3），得：a+b+c+e+f+g=28，（a+b+c+d+e+f+g+h ）-（d+h ）=28，d+h=（1+2+3+4+5+6+7+8）-28=8，由（2）+（4），同样可得b+f=8， 又1，2，3，4，5，6，7，8中有1+7=2+6=3+5=8.又1要出现在顶点上，d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性，不妨设b=2，f=6，d=3，h=5. a ，c ，e ，g 可取到1，4，7，8若a=1，则c=14-（1+2）=11，不在1，4，7，8中，不行.若c=1，则a=14-（1+2）=11，不行. 若e=1，则c=14-（1+3）=10，不行. 若g=1，则a=8，c=4，e=7. 说明：例题为封闭型数阵，由它的分析思考过程可以看出，确定各边顶点所应填的数为封闭型数8765432187654321（）（2）h gf ed c ba阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数，使得三条边上的三个数的和都是12，若A 、B 、C 的和为18，则三个顶点上的三个数的和是 。

第二讲：数字游戏—填图与拆数【有话要说】 填数是一种既有趣， 又能锻炼头脑、 发展智力的趣味活动。

它不仅可以提高你的运算能力， 而且能促使你积极地去思考问题，解决问题。

填数这类题目的题型比较多，解答时除了口算要熟练外，更重要的是要会分析、推理。

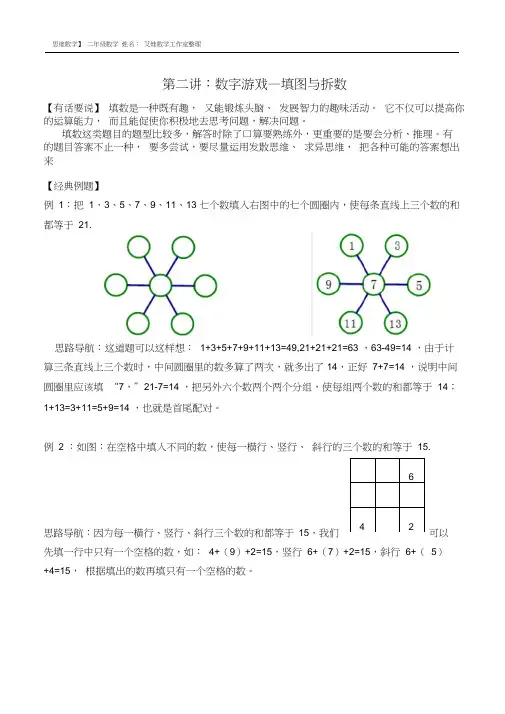
有 的题目答案不止一种， 要多尝试，要尽量运用发散思维、 求异思维， 把各种可能的答案想出来【经典例题】例 1：把 1、3、5、7、9、11、13 七个数填入右图中的七个圆圈内，使每条直线上三个数的和 都等于 21.思路导航：这道题可以这样想： 1+3+5+7+9+11+13=49,21+21+21=63 ，63-49=14 ，由于计 算三条直线上三个数时，中间圆圈里的数多算了两次，就多出了 14，正好 7+7=14 ，说明中间 圆圈里应该填 “7，”21-7=14 ，把另外六个数两个两个分组，使每组两个数的和都等于 14；1+13=3+11=5+9=14 ，也就是首尾配对。

例 2 ：如图：在空格中填入不同的数，使每一横行、竖行、 斜行的三个数的和等于 15.思路导航：因为每一横行、竖行、斜行三个数的和都等于 15，我们可以先填一行中只有一个空格的数，如： 4+（9）+2=15，竖行 6+（7）+2=15，斜行 6+（ 5）+4=15， 根据填出的数再填只有一个空格的数。

64281 6 35 7 492例 3：把 1、2、3、4、5、6 这六个数填入右图的圆内，使每个大圆的四个数的和都等于 13思路导航：先确定图形中央的两个数分别填几， 可以这样想， 先求六个数的和与两个大圆上八 个数的和：1+2+3+4+5+6=21,13+13=26,26-21=，5这个 5 就是中央两个圆的数的和，1+4=5,2+3=5，就是说中央两个小圆里可以填 1 和 4，也可以填 2 和 3，中央填 1 和 4,13-5=8，左边填 3 和5， 右边填 2和6，中央填 2和3行不行呢？剩下的数有 1、4、5、6任意两个数的和都不是 8，所 以无法填出，因此，中央只能填 1和 4.解：例 4 ：由图中三个圆圈两两相交形成七个部分，分别填上自然数 3、5、7 三个数已填好，请填上其余各数，使每个圆圈中四个数的和都是 15.解：1～7 七个自然数，在一些部分中，思路导航：图中空着四个部分要填入四个数：1、2、4、6，可以看出中心部分属三个圆圈公共部分，关键 要确定中心填哪个数，我们用拆数的方法来确定。

数阵图【2 】1.应用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,统一个数字不能反复消失.(1)填数,使横行.竖行的三个数(2)填数,使每条线上的三个数相加都得11. 之和都得15.2.在每个方格中填入恰当的数,使每一横行.竖行的和以及两斜行的三个数之和都是18.在空格中填入恰当的数,使横行和竖行或每条对角线上的三个数相加都等于15.3.把3,4,5,6,7这五个数分离填入下面的空格里,使横行.竖行的三个数之和都等于14.拓展演习（1）把2,3,4,5,6这五个数分离填入圆圈中,使每条线上三个数相加的和都等于12.（2）把1,2,3,4,5,6分离填入○里,使每一个大椭圆上的四个数之和等于13.例4.把1,3,5,7,9,11,13这七个数分离填入○里,使每条直线上的三个数相加的和都为17.简略数阵图例1.把1—5 这五个数分离填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9.例2.把1—7这七个数分离填入图中的各○内,使每条线段上三个○内数的和等于10.例 3.鄙人图圆圈内分离填入数字1~9,使两条直线上五个数的和相等,和是若干？例4.把1～6这六个数分离填鄙人图中三角形三条边的六个○内,使每条边上三个○内数的和等于9.例5.将2—9这八个数分离填入右图的○里,使每条边上的三个数之和都等于18.例6.将1.2.3.4.5.6.7.8.9九个数字分离填入图中的小圆圈中,使三角形每边上四个数的和是17.1.把2—6 这五个数分离填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于13.2.在图中填入2—9,使每边3个数的和等于15.3.将数字1—9分离填在图中的○内使每条线上五个○内数的和等于27.4.把1.4.7.10.13.16.19七个数填入图中7朵花里,使每条线上三个数的和等于30.。

第十七周数阵图把一些数字按照一定的要求，排列成各种各样的图形，叫做数阵图。

数阵是由幻方演化出来的另一种数字图。

幻方一般均为正方形。

图中纵、横、对角线数字和相等。

数阵则不仅有正方形、长方形，还有三角形、圆、多边形、星形、花瓣形、十字形，甚至多种图形的组合。

变幻多姿，奇趣迷人。

一般按数字的组合形式，将其分为三类，即辐射型数阵、封闭型数阵、复合型数阵。

【解题技巧】数阵的分类：封闭型：封闭型数阵图的解题突破口，是确定各边顶点所应填的数。

为确定这些数，采用的方法是建立有关的等式，通过以最小值到最大值的讨论，来确定每条边上的几个数之和，再将和数进行拆分以找到顶点应填入的数，其余的数再利用和与顶点的数就容易被填出。

（1—6）辐射型：辐射型数阵图，解法的关键是确定中心数。

具体方法是：通过所给条件建立有关等式，通过整除性的讨论，确定出中心数的取值，然后求出各边上数的和，最后将和自然数分拆成中心数的若干个自然数之和，确定边上其他的数。

复合型：复合型数阵图，解题的关键是要以中心数和顶点数为突破口。

数阵的特点：每一条直线段或由若干线段组成的封闭线上的数字和相等。

它的表达形式多为给出一定数量的数字，要求填入指定的图中，使其具备数阵的特点。

解数阵问题的一般思路是：1.求出条件中若干已知数字的和。

2.根据“和相等”，列出关系式，找出关键数——重复使用的数。

3.确定重复用数后，对照“和相等”的条件，用尝试的方法，求出其他各数。

有时，因数字存在不同的组合方法，答案往往不是唯一的。

【铜牌例题】将2、3、4、5、6、7、8、9、10填入下图中的9个方格中，使每行、每列及对角线之和相等，小明已经填了5个数，请将其余4个数填入。

【答案】【解析】先根据最左边一列求出幻和，然后根据这个和和给出的数字逐步推算。

3+8+7=18；第二行中间的数是：18-8-4=6；第三行中间的数是：18-7-9=2；第一行第一个数是：18-4-9=5；第一行中间的数是：18-3-5=10；【举一反三1】（第十届走美杯初赛）小华需要构造一个3×3的乘积魔方，使得每行、每列、每条对角线上三个正整数的乘积都相等；现在他已经填入了2，3，6三个数，那当小华的乘积魔方构造完毕后，x等于______。

在神奇的数学王国里，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷．它就是数阵图．到底什么是数阵图呢？我们先观察下面两个图：数阵图就是将一些数按照一定要求排列而成的某种图形．它一般分为辐射型(图1)和封闭型(2)两种．要把一些数字按一定的规则填入图形中，并不是一件容易的事，这需要我们多观察，找关系，仔细推理才能完成．下面我们就一起来找一找数阵图的秘密吧！如图，在空格中填入2、3、4、5，使横行和竖行三个数的和都等于8。

【解答】如图，在空格中填入1、2、4、5，使横行和竖行三个数的和都等于9。

【解答】知识分类一：基础数阵图113325341245如图：在空格中填入不同的数，使每一横行、竖行、斜行的三个数的和等于15。

【解答】将2，4，6，7，8，10分别填入图中空格，使每一个横行、竖行、斜行的三个数的和等于18。

【解答】81 8 7935 7 26 104把1、3、5、7、9、11、13七个数填入下图中的七个圆圈内，使每条直线上三个数的和都等于21。

【解答】这道题可以这样想：1+3+5+7+9+11+13=49,21+21+21=63，63-49=14，由于计算三条直线上三个数时，中间圆圈里的数多算了两次，就多出了14，正好7+7=14，说明中间圆圈里应该填“7”，21-7=14，把另外六个数两个两个分组，使每组两个数的和都等于14；1+13=3+11=5+9=14，也就是首尾配对。

把1、2、3、7、8、9这六个数分别填在下面图中的○里，使每条直线上三个数的和都相等。

【答案】把1、2、3、4、5、6这六个数填入下图的圆内，使每个大圆的四个数的和都等于13。

【答案】58219753知识分类二：数阵图进阶213645把10、20、30、40、50、60、70、80这八个数填入下图的圆圈里，使每个大圆上的五个数的和都是200.【答案】在圆圈内填上1～8这八个数字，使长方形每条边上三个数的和为12.【答案】703080401020605024675381将1、2、3、4、5、6这六个数填在下面的圆圈里，使每条线上三个数的和等于9.【答案】由图中三个圆圈两两相交形成七个部分，分别填上1～7七个自然数，在一些部分中，自然数3、5、7三个数已填好，请填上其余各数，使每个圆圈中四个数的和都是15.【答案】34256137521 3754 6将10、14、6填入下图，使每个圆圈中四个数的和都是30.【答案】412288126210144。

二年级奥数：数阵图渣渣兔摆棋子，它想让每行每列的三个数相加都等于 15。

现在摆了 4 个，剩下的应该摆哪几个数呢？数阵图——把数按照一定的规律要求排起来方法：找准要求和填数的突破口庆祝渣渣兔的生日，微微老师给它做了一个蛋糕。

现在往蛋糕上插上数字蜡烛，希望每条线上的三个数相加和都等于 12。

你来帮帮我！辐射型数阵图关键点：重叠数如果所填的数是连续数，可以尝试重叠数为最大的、最小的、中间数其余的：大手拉小手请把 1、2、3、4、5、6、7 这七个数分别填入圆圈里，使每条直线上的三个数相加的和都是 12。

请把 1~9 这九个数字分别填入圆圈内，使每条横线、竖线、斜线上的三个数相加的和都是12。

请你把 1、2、3、5、7、9、11 这 7 个数分别填入圆圈里，使每条直线上的三个数相加的和都是 14。

辐射型数阵图（一个重叠点）如果所填的数不是连续数，用拆数法，将总数拆成几个数相加的形式。

请你把 1、2、3、4、5、7 分别填入圆圈里，使每一个大椭圆上的四个数之和等于 13。

封闭型数阵图（多个重叠数）方法：有序的拆数（重复的数就是数阵图中的重叠数）数阵图，关键点是找出重叠数1、辐射型——连续的数：尝试法：头、尾、中间数；其余大手拉小手不连续的数：拆数法2、封闭型——拆数法【练习 1】在圆圈内填上适当的数，使每条线上的三个数之和都为 12。

你能做到吗？【练习 2】把 4~8 这 5 个数填入圆圈中（左下图），使两条直线上三个数之和等于 18。

【练习 3】将 1-7 这 7 个数填入右上图中，使每条线上的数之和都未 14。

【练习 4】请将 3、4、5、6、7、8、9 填入下面的圆圈里，并使每条直线上三个数字之和都相等。

（同一图片中不能出现相同的数；不同图片中数字可以重复使用。

）【练习 5】请你把 1、2、3、4、5、6 分别填入圆圈里，使每一个大椭圆上的四个数之和等于 14。

二年级奥数：数阵图渣渣兔摆棋子，它想让每行每列的三个数相加都等于 15.现在摆了 4 个，剩下的应该摆哪几个数呢？数阵图——把数按照一定的规律要求排起来方法：找准要求和填数的突破口庆祝渣渣兔的生日，微微老师给它做了一个蛋糕.现在往蛋糕上插上数字蜡烛，希望每条线上的三个数相加和都等于 12.你来帮帮我！辐射型数阵图关键点：重叠数如果所填的数是连续数，可以尝试重叠数为最大的、最小的、中间数其余的：大手拉小手请把 1、2、3、4、5、6、7 这七个数分别填入圆圈里，使每条直线上的三个数相加的和都是 12.请把 1~9 这九个数字分别填入圆圈内，使每条横线、竖线、斜线上的三个数相加的和都是12.请你把 1、2、3、5、7、9、11 这 7 个数分别填入圆圈里，使每条直线上的三个数相加的和都是 14.辐射型数阵图（一个重叠点）如果所填的数不是连续数，用拆数法，将总数拆成几个数相加的形式.请你把 1、2、3、4、5、7 分别填入圆圈里，使每一个大椭圆上的四个数之和等于 13.封闭型数阵图（多个重叠数）方法：有序的拆数（重复的数就是数阵图中的重叠数）数阵图，关键点是找出重叠数1、辐射型——连续的数：尝试法：头、尾、中间数；其余大手拉小手不连续的数：拆数法2、封闭型——拆数法【练习 1】在圆圈内填上适当的数，使每条线上的三个数之和都为 12.你能做到吗？【练习 2】把 4~8 这 5 个数填入圆圈中（左下图），使两条直线上三个数之和等于 18.【练习 3】将 1-7 这 7 个数填入右上图中，使每条线上的数之和都未 14.【练习 4】请将 3、4、5、6、7、8、9 填入下面的圆圈里，并使每条直线上三个数字之和都相等.（同一图片中不能出现相同的数；不同图片中数字可以重复使用.）【练习 5】请你把 1、2、3、4、5、6 分别填入圆圈里，使每一个大椭圆上的四个数之和等于 14.。

简单数阵图一、辐射型数阵图从一个中心出发，向外作若干条射线，在每条射线上安放同样多个数，使其和是一个不变的数。

突破关键：确定中心数，多算的次数，公共的和。

先求重叠数。

数总和+中心数×重复次数＝公共的和×线数重叠部分=线总和-数总和/线总和=公共的和×线数数和：指所有要填的数字加起来的和中心数：指中间那数字，即重复计算那数字（重叠数）重复次数：中心数多算的次数，一般比线数少1公共的和：指每条直线上几个数的和线数：指算公共和的线条数例1、把1-5这五个数分别填在左下图中的方格中，使得横行三数与竖列三数之和都等于9。

例2、把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。

分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于9，所以：总和数=(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。

分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。

所以，必须先求出这个“和”。

根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。

例3、把1~5这五个数填入右图中的○里，使例4、将1~7这七个自然数填入左下图的每条直线上的三个数之和相等七个○内，使得每条边上的三个数之和都等于10。

分析与解：例1是知道每条直线上的三数之和，不知道重叠数；例2是知道重叠数，不知道两条直线上的三个数之和；本例是这两样什么都不知道。

但由例1、例2的分析知道，(1+2+3+4+5)+重叠数=每条直线三数之和×2，每条直线上三数之和=(15+重叠数)÷2。

简 单 数 阵 图一、辐射型数阵图从一个中心出发，向外作若干条射线，在每条射线上安放同样多个数，使其和是一个不变的数。

突破关键：确定中心数，多算的次数，公共的和。

先求重叠数。

数总和 + 中心数×重复次数＝公共的和×线数重叠部分 = 线总和 - 数总和 / 线总和 = 公共的和×线数数 和：指所有要填的数字加起来的和中 心 数：指中间那数字，即重复计算那数字（重叠数）重复次数：中心数多算的次数，一般比线数少1公共的和：指每条直线上几个数的和线 数：指算公共和的线条数例1、把1-5 这五个数分别填在左下图中的方格中，使得横行三数与竖列三数之和都等于9。

例2、把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。

分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于9，所以：总和数=(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。

分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。

所以，必须先求出这个“和”。

根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于 [(1+2+3+4+5)+5]÷2=10。

例3、把1~5这五个数填入右图中的○里，使每条直线上的三个数之和相等 例4、将1~7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于10。

分析与解：例1是知道每条直线上的三数之和，不知道重叠数；例2是知道重叠数，不知道两条直线上的三个数之和；本例是这两样什么都不知道。

但由例1、例2的分析知道， (1+2+3+4+5)+重叠数=每条直线三数之和×2， 每条直线上三数之和=(15+重叠数)÷2。

数阵图数阵图：就是将一些数按照一定要求排列而成的某种图形。

分为：封闭型、辐射型、复合型。

例如：特点：直线上的数字和相等。

名词：边和，重叠数(阵眼)(★★)将1~7这七个数字，分别填入图中各个○内，使每条线段上的三个○内数的和都等于14。

(★★★)把1～9这9个数分别填入下图的圆圈中，使得每条直线上的3个数的和都相等。

(★★★)将1~8这8个数分别填入下图中，使两个大圆上4个数的和都相等，那么这个和最大＝______。

(★★★)请将1、2、4、6这四个数填入到下图中各空白区域内，使得每个圆圈里的四个数字和都等于15。

【铺垫】(★★)把1至8分别填入图的八个方格内，使得各列上两个数之和都相等，各行四个数之和也相等。

(★★★★★)请将数字1、2、3、4、5、6、7填在下图，使得每个圆圈上的三个数字之和与每条直线上的三个数之和相等。

【超常大挑战】(★★★★★)有一个长方形的城堡，四周有10个掩体。

守城的士兵有10件武器，各种武器的威力如下表。

为了使城堡四边上的武器威力总数都相同，并且尽量大，应如何在十个掩体中配备武器？【知识大总结】数阵图1．特点，新名词。

2．口诀1：数边和，看重叠，列等式，整除关系推一推等式：边和×次数＝数字和＋重叠数×(次数－1)本质：找边和与数字和、重叠数三者关系难点：重叠数有几个，各自用了多少次。

3．口诀2：掐头、去尾、取中间，首尾配对组相等。

适用：等差数列填入到放射型数阵图中。

4．复合型数阵图，先满足部分，保证不破坏已有边和前提下，微调，满足全部。

【今日讲题】例2，例3，例5【讲题心得】___________________________________________________________________________________________ ___________________________________________________________________________________________ __________________________________________________________________________________________。