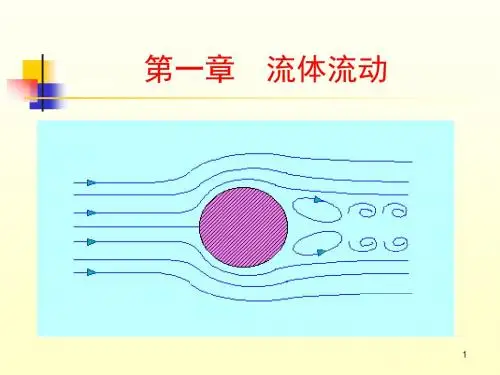
第一章流体与流体中的传递现象特征流体 (Fluid) 与流体流动 (Flow) 的基本概念在航空、航天、航海，石油、化工、能源、环境、材料、医学和生命科学等领域，尤其是化工、石油、制药、生物、食品、轻工、材料等许多生产领域以及环境保护和市政工程等，涉及的对象多为流体。
“流程工业”在流动之中对流体进行化学或物理加工 加工流体的机器与设备过程装备物质的三种常规聚集状态：固体、液体和气体物质外在宏观性质由物质内部微观结构和分子间力所决定物质的三种形态分子的随机热运动和相互碰撞给分子以动能使之趋于飞散分子间相互作用力的约束以势能的作用使之趋于团聚两种力的竞争结果决定了物质的外在宏观性质。
而这两种力的大小与分子间距有很大关系。
约为1×10-8 cm （分子尺度的量级），分子间相互作用势能出现一个极值称为“势阱”，即分子的结合能，其值远远大于分子平均动能。
分子力占主导地位，分子呈固定排列分子热运动仅呈现为平衡位置附近的振荡。
有一定形状且不易变形。
分子间距液体：分子热运动动能与分子间相互作用势能的竞争势均力敌。
分子间距比固体稍大1/3左右。
不可压缩、易流动。
气体：分子间距约为3.3×10-7cm （为分子尺度的10倍）。
分子平均动能远远大于分子间相互作用势能，分子近似作自由的无规则运动。
有易流动、可压缩的宏观性质。
超临界流体、等离子体 流体固体连续介质假定(Continuum hypotheses)Vm V V ∆∆=∆→∆lim 0ρ∆V 0：流体质点或微团。
尺度远小于液体所在空间的特征尺度，而又远大于分子平均自由程连续介质假定：流体微团连续布满整个流体空间，从而流体的物理性质和运动参数成为空间连续函数流体是由离散的分子构成的，对其物理性质和运动参数的表征是基于大量分子统计平均的宏观物理量平均质量 注：该假定对绝大多数流体都适用。
但是当流动体系的特征尺度与分子平均自由程相当时，例如高真空稀薄气体的流动，连续介质假定受到限制。
场力或体积力（质量力）：非接触力，大小与流体的质量成正比，例如：重力，离心力，电磁力等表面力：接触力，大小与和流体相接触的物体（包括流体本身）的表面（或假想表面）积成正比，例如：压强和应力 a a F V m ρ==处于重力场中的流体， 无论运动与否都受到力的作用。
连续介质的受力服从牛顿定律。
重力场——重力加速度离心力场——离心加速度压强被视为外部作用力（包括流体柱自身的重力）在流体中的传播，其方向始终与作用面相垂直；无论流体运动与否，压强始终存在，静止流体中的压强称为静压强。
在流体空间的任一点处，静压强数值相等地作用在各个方向。
⎩⎨⎧-+=真空度表压大气压强真实压强正应力：与压缩（或扩张）形变相对应的应力，方向与作用面相垂直。
剪应力：与剪切形变相对应的应力，方向与作用面相平行。
表面张力：存在于不同流体的相邻界面，使液体表面具有收缩的趋势。
其大小用表面张力系数 σ 来表示，其单位为N/m 。
其大小对于流体的分散和多相流动与传热传质有重要影响。
用压力计（manometer ）测定压强当真实压强大于大气压强时称为表压、当真实压强小于大气压强时称为真空度。
流体受力会产生形变单组分与多组分 （single and multicomponent ） 单相流与多相流 （ single and multiphase ）单组分体系只含有一种物质，组成均匀且无化学反应 。
例：纯水、氧气、氮气等，空气有时也被视作单组分体系。
多组分体系中各物质有浓度变化及由此引起的体系性质改变。
单相流体系：体系所含的物质只有一种相态，其主要特征是体系内部不存在相界面及相间传递，体系的各种性质在空间连续分布。
多相流体系：体系内含两种或两种以上相态的物质，其主要特征是体系内存在气(汽)-液、气-固或液-固、液-液相界面，且界面上的传递速率对体系的性质具有重要影响。
三维、二维与一维体系非稳态与稳态（Steady and unsteady ）按流动参数随空间坐标变化的特征来区分流动体系。
严格说流体流动都是在三维空间中进行，因此流动参数（浓度、密度、温度、速度、压力、……）都是三维空间座标的连续函数。
T = f(x,y,z) 三维 (three-dimensional ，3D) 可根据体系的流动特征将其简化为T = f(x,y) 二维 (two-dimensional ，2D)T = f(x) 一维 (one-dimensional)非稳态流动：流动参数随时间而变化， T = f(x,y,z,t)； 稳态流动：流动参数不随时间变化， T = f(x,y,z) 。
层流与湍流(Laminar and Turbulent Flow) 雷诺实验层流：流体质点很有秩序地分层顺着轴线平行流动，不产生流体质点的宏观混合。
湍流：流体质点沿管轴线方向流动的同时还有任意方向上的湍动，因此空间任意点上的速度都是不稳定的，大小和方向不断改变。
层流与湍流(Laminar and Turbulent Flow)u ut 湍流流体的流速波形反映了湍动的强弱与频率，同时也说明宏观上仍然有一个稳定的时间平均值。
其它参数如温度、压强等也有类似性质。
湍流的特点对直管内的流动而言：μρdu Re =雷诺准数的定义流型判别的依据——雷诺准数(Reynolds number)流型的判别黏性力动力==duuμρ2Re < 2000 稳定的层流区2000 < Re < 4000 由层流向湍流过渡区Re > 4000 湍流区流体流动受固体壁面影响（能感受到固体壁面存在）的区域 流动边界层 (Boundary Layer)内摩擦：一流体层由于粘性的作用使与其相邻的流体层减速 边界层：受内摩擦影响而产生速度梯度的区域（δ）u =0.99u 0 边界层发展：边界层厚度δ 随流动距离增加而增加 流动充分发展：边界层不再改变，管内流动状态也维持不变 充分发展的管内流型属层流还是湍流取决于汇合点处边界层内的流动属层流还是湍流 X o u o δδδd进口段圆管入口处的流动边界层发展平板上的流动边界层发展流动边界层的发展注意：层流边界层和层流内层的区别层流边界层 湍流边界层层流内层边界层界限u 0 u 0 u 0 x y层流边界层：边界层内的流动类型为层流 湍流边界层：边界层内的流动类型为湍流 层流内层：边界层内近壁面处一薄层，无论边界层内的流型为层流或湍流，其流动类型均为层流倒流分离点u0DAC’CBxAB：流道缩小，顺压强梯度，加速减压BC：流道增加，逆压强梯度，减速增压CC’以上：分离的边界层CC’以下：在逆压强梯度的推动下形成倒流，产生大量旋涡热力学第二定律指出，所有系统由非平衡态向平衡态转化是熵增大的自发过程，例如： 热流从高温处流向低温处 水流从高位处流向低位处 电流由高电位流向低电位现象方程（Phenomenological equation ）：［扩散通量］＝－［扩散系数］·［扩散推动力］ 传输阻力传输推动力传输速率=lU A I d d d d γ-=扩散现象与扩散定律Diffusion phenomena and diffusion lawsd I /d A —— 电流通量，微分时间内垂直通过微元面积的电流量 d U /d l —— 电位梯度，微元长度上电流流动的推动力 γ —— 电导率，电阻率的倒数动量扩散与牛顿粘性定律Momentum diffusion and Newtonian viscous law单组分气体、一维、等温层流流动体系中的动量扩散现象 层流流体中由速度梯度推动的扩散称为分子动量扩散u m 动量 y u x d d 速度梯度 )(y u x 速度分布动量为一矢量，其方向就是流速的方向，一维流动情况下可定为 x 轴的正向。
而动量扩散的方向，则由速度梯度决定、并且指向速度降低的方向。
y u x , T, ρA λλ u x (y), T(y), ρA (y) ou nMu xr x =ρ宏观上，分子数密度为 n 、分子量为 M r 的气体的动量浓度(即单位体积流体具有的动量)为根据分子动理学原理 在气体密度均匀的条件下，动量浓度 ρ u x 仅取决于流体所在位置处的宏观流速 u x (y )流动气体分子的运动流体的宏观运动，u x 迭加在宏观运动上的分子微观热运动，其均方根速度为 v λ微观上，分子无规热运动引起气体分子之间的碰撞和动量交换，力图使动量浓度趋于均匀，由此而导致了流速不同的流体层与层之间在 y 方向上的动量传递。
厚度均不超过分子平均自由程 λ（即保证 y 方向上气体分子的每一次迁移运动都会在两层流体之间产生动量交换）yu x , T, ρAλλu x (y), T(y), ρA (y)oy考察任意 y 位置处相邻的两层气体在该微小尺度范围内流体宏观流速分布函数可视为线性，即两层流体的流速分别为 u x 和 u x + λ（d u x / d y ）u x +λ(d u x / d y )u x3n vλ33ρνλλ=r nM v 分子数通量 质量通量取位于上层的单位微元体积的流体为体系，从统计平均的观点，与相邻的下层流体在 y 方向上通过单位微元底面积在单位时间内交换的通量为由于分子无规热运动在三维空间各向同性并且气体密度维持均匀，因此 y 方向上的分子无规热运动具有等分子数、反方向交换的特征。
动量扩散通量⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-y u u u v x x x d d 3λρλ()y u yu y u u u v x x x x x yx d d 31d d 31d d 31ρλνλρνλρτλλλ-=-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=根据牛顿第二定律，运动体系的动量变化率等于作用在该体系上的力，动量变化率的方向与力的方向相同运动粘度 Kinematic viscosity 3λνλv =剪应力（shear stress ） τyx ：表示平行作用于单位面积上的切向力，下标 x 代表剪应力或者动量的方向，y 代表力的作用面的法线方向或者动量传递的方向。
()yu x d d ρ动量浓度梯度()yu x yxd d ρντ-=动量扩散系数 动量扩散通量的推动力yu xyxd d μτ-= 1 10 100 1000 100001010.10.010.001甘油水空气剪切速率/ s -1剪应力τ/ N .m -2—— 牛顿粘性定律对实际气体和液体，动量扩散的机理更复杂，但一般能满足满足牛顿粘性定律的流体称为牛顿流体（Newtonian fluid ）μ =ρν 动力粘度（viscosity ）牛顿粘性定律与牛顿流体（Newtonian fluid ）⎪⎪⎭⎫ ⎝⎛==y u f y u d d /d d τμ高分子熔体和溶液、表面活性剂溶液、石油、食品以及含微细颗粒较多的悬浮体、分散体、乳浊液等流体在层流时并不服从牛顿粘性定律，统称为非牛顿流体非牛顿流体的粘度 μ 不再为一常数而与 d u x / d y 有关牛顿型流体塑型流体涨塑流体假塑型流体d u/d yττy宾汉塑性流体（Bingham plastics ）yuK y d d +=τττy —— 屈服应力（threshold shear stress ）K —— 宾汉粘度yuy u yuK an d d d d d d 1μτ-=-=-n —— 流变指数（flow behavior index ）K —— 稠度系数（flow consistency index ） μa —— 表观粘度幂律（power law ）流体n<1 —— 假塑性流体（Pseudoplastic fluid ） n=1 —— 牛顿流体（Newtonian fluid ） n>1 —— 涨塑性流体（Dilatant fluid ）—— 傅立叶热传导定律Tc T c nM p p r ρ=()y T c y T c y T T T c nM q pp p r d d 31d d 31d d 31ρλνλρνλνλλλ-=-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-=yT k q d d -=c k pαρ=导热系数（Thermal conductivity ）热量扩散与傅立叶热传导定律 (Heat diffusion and Fourier’s law)热量浓度()yT c q p d d ρα-=热量扩散通量的推动力()yT c p d d ρ3λαλv =热量扩散系数 热量浓度梯度—— 费克第一扩散定律扩散系数()y w y w y w w w nM j A A A A A r ABd d 31d d 31d d 31ρλνλρνλνλλλ-=-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-=3AB λνανλ===D ()yw D j A ABABd d ρ-=()()y w nM y w r A A A ==ρρ质量扩散与费克定律 (Mass diffusion and Fick’s law) 质量浓度质量浓度梯度 质量互扩散系数 3AB λλv D =()yw d d A ρ质量扩散通量的推动力流体运动的描述方法拉格郎日（Lagrange, J. 1736-1813）法：把流体的运动看作是无数个质点运动的总和，以个别质点为观察对象加以描述，整个流动为各质点运动的汇总。
