1化工原理流体流动解析

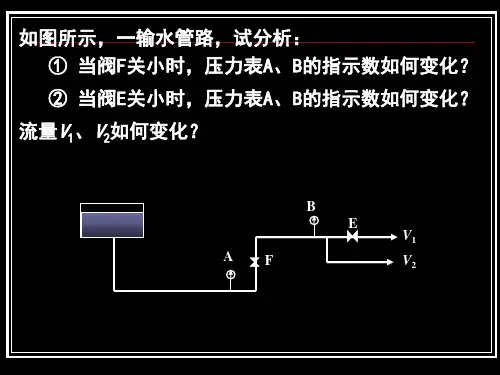
一、单选题1．单位体积流体所具有的（）称为流体的密度。

AA 质量；B 粘度；C 位能；D 动能。

2．单位体积流体所具有的质量称为流体的（）。

AA 密度；B 粘度；C 位能；D 动能。

3．层流与湍流的本质区别是（）。

DA 湍流流速＞层流流速；B 流道截面大的为湍流，截面小的为层流；C 层流的雷诺数＜湍流的雷诺数；D 层流无径向脉动，而湍流有径向脉动。

4．气体是（）的流体。

BA 可移动；B 可压缩；C 可流动；D 可测量。

5．在静止的流体内，单位面积上所受的压力称为流体的（）。

CA 绝对压力；B 表压力；C 静压力；D 真空度。

6．以绝对零压作起点计算的压力，称为（）。

AA 绝对压力；B 表压力；C 静压力；D 真空度。

7．当被测流体的（）大于外界大气压力时，所用的测压仪表称为压力表。

DA 真空度；B 表压力；C 相对压力；D 绝对压力。

8．当被测流体的绝对压力（）外界大气压力时，所用的测压仪表称为压力表。

AA 大于；B 小于；C 等于；D 近似于。

9．（）上的读数表示被测流体的绝对压力比大气压力高出的数值，称为表压力。

AA 压力表；B 真空表；C 高度表；D 速度表。

10．被测流体的（）小于外界大气压力时，所用测压仪表称为真空表。

DA 大气压；B 表压力；C 相对压力；D 绝对压力。

11. 流体在园管内流动时，管中心流速最大，若为湍流时，平均流速与管中心的最大流速的关系为（）。

BA. Um＝1/2Umax；B. Um＝0.8Umax；C. Um＝3/2Umax。

12. 从流体静力学基本方程了解到U型管压力计测量其压强差是( )。

AA. 与指示液密度、液面高度有关，与U形管粗细无关；B. 与指示液密度、液面高度无关，与U形管粗细有关；C. 与指示液密度、液面高度无关，与U形管粗细无关。

13.层流底层越薄( )。

CA. 近壁面速度梯度越小；B. 流动阻力越小；C. 流动阻力越大；D. 流体湍动程度越小。

化工原理流体流动知识点总结化工原理中的流体流动是指在化工过程中物质（气体、液体或固体颗粒）在管道、设备或反应器中的运动过程。

了解流体流动的知识对于化工工程师来说至关重要。

下面是关于流体流动的一些重要知识点的总结。

1.流体的物理性质：-流体可以是气体、液体或固体颗粒。

气体和液体的主要区别在于分子之间的相互作用力和分子间距。

-流体的物理性质包括密度、黏度、表面张力、压力和流速等。

2.流体的运动方式：- 流体的运动可以是层流（Laminar flow）或紊流（Turbulent flow）。

-在层流中，流体以平行且有序的方式流动，分子之间的相互作用力主导着流动。

-在紊流中，流体以非线性和混乱的方式运动，分子之间的相互作用力相对较小，惯性和湍流运动主导着流动。

3.流体的流动方程：-流体流动可以通过连续性方程、动量方程和能量方程来描述。

-连续性方程（质量守恒方程）描述了流体在空间和时间上的质量守恒关系。

-动量方程描述了流体中的力平衡关系，包括压力梯度、黏度和惯性力等因素。

-能量方程描述了流体中的能量守恒关系，包括热传导、辐射和机械能转化等因素。

4.管道流动：-管道中的流体流动可以是单相（单一组分）或多相（多个组分）。

-管道流动的主要参数包括流速、压力损失和摩阻系数等。

- 常用的管道流动方程包括Bernoulli方程、Navier-Stokes方程和Darcy-Weisbach方程等。

5.流体输送：-流体输送是指将流体从一个地点输送到另一个地点的过程。

-在流体输送中，常用的设备和装置包括泵、压缩机、阀门、流量计和管道系统等。

-输送过程中要考虑流体的性质、流速、压力损失以及设备的选型和操作条件等因素。

6.流体混合与分离：-流体混合和分离是化工过程中常见的操作。

-混合可以通过搅拌、喷淋、气体分散等方法实现。

-分离可以通过过滤、沉淀、蒸馏、萃取和膜分离等方法实现。

7.流体力学实验：-流体力学实验是研究流体流动和相应现象的方法之一-常用的流体力学实验包括流速测量、压力测量、流动可视化和摩擦系数测定等。

化工原理流体流动化工原理是化学工程领域的基础，其中包括了化工原理流体流动。

通过深入理解和掌握流体流动的原理，我们可以更好地设计、优化和控制化工流程的运行。

本文将介绍流体流动的基本概念、流体的运动方式、流场的描述和流体运动的控制等内容。

一、流体流动的基本概念流体是指能够流动的物质，包括了气体和液体。

流体流动是指流体在空间或管道中的运动过程。

在流体流动中，流体分子与周围分子不断碰撞，产生微小的能量转移和动量转移，从而引起流体的整体运动。

流体流动可分为定常流、非定常流和稳定流等几种类型。

其中，定常流指的是流动过程中各种物理量（如质量、能量、动量等）随时间不变的情况；非定常流则与定常流相反，各种物理量会随时间或空间变化；稳定流是指虽然物理量会随时间变化，但整个流动过程仍然是稳定的，即不出现突然的萎缩或涌流等现象。

流体流动过程中会出现速度、压力、密度等物理量的变化，这些变化可用流体力学方程式来描述和计算。

其中，质量守恒定律、动量守恒定律和能量守恒定律是描述流体流动的基本方程式。

二、流体的运动方式流体的运动方式包括了分子运动、分子间相互作用和运动量转移等几种。

在分子运动方面，气体分子之间距离较大，运动自由度高；而液体分子之间距离较近，分子运动更加有限。

流体的运动始终与分子相互作用有关。

在空气中，分子间间隔很大，因此分子之间的相互作用不太重要。

但在液体中，分子之间的相互作用较为紧密，从而导致液体的可压缩性低于气体。

在运动量转移方面，流体运动时会发生质量、能量和动量的转移。

其中，质量转移是指流体中的物质在空间中的传递过程，能量转移则是指流体在不同地点和不同形态之间转移热能，而动量转移则是指流体分子的运动量在不同地点之间的转移。

三、流场的描述流场是指流体的物理状态和运动状态。

在流动过程中，流体分子会产生不同的物理量变化，因此需要对流场进行描述。

在描述流场时，可使用不同的数学工具和方法。

其中，流线、等势线、流函数、速度势和压力势是比较常用的方法。

课后解析化工原理学院：环境与化学工程学院班级：化学工程与工艺1201班学号：姓名：日期： 2014年6月20日第一章流体流动2．在本题附图所示的储油罐中盛有密度为 960 ㎏/㎥的油品，油面高于罐底 6.9 m，油面上方为常压。

在罐侧壁的下部有一直径为 760 mm 的圆孔，其中心距罐底 800 mm，孔盖用14mm的钢制螺钉紧固。

若螺钉材料的工作应力取为39.23×106 Pa ，问至少需要几个螺钉？分析：罐底产生的压力不能超过螺钉的工作应力即P油≤σ螺解：P螺 = ρgh×A = 960×9.81×(9.6-0.8) ×3.14×0.762150.307×103 Nσ螺 = 39.03×103×3.14×0.0142×nP油≤σ螺得 n ≥ 6.23取 n min= 7至少需要7个螺钉3．某流化床反应器上装有两个U 型管压差计，如本题附图所示。

测得R1 = 400 mm ， R2 = 50 mm，指示液为水银。

为防止水银蒸汽向空气中扩散，于右侧的U 型管与大气连通的玻璃管内灌入一段水，其高度R3= 50 mm。

试求A﹑B两处的表压强。

分析：根据静力学基本原则，对于右边的Ｕ管压差计，a–a′为等压面，对于左边的压差计，b–b′为另一等压面，分别列出两个等压面处的静力学基本方程求解。

解：设空气的密度为ρg，其他数据如图所示a–a′处 P A + ρg gh1 = ρ水gR3 + ρ水银ɡR2由于空气的密度相对于水和水银来说很小可以忽略不记即：P A = 1.0 ×103×9.81×0.05 + 13.6×103×9.81×0.05= 7.16×103 Pab-b′处 P B + ρg gh3 = P A + ρg gh2 + ρ水银gR1P B = 13.6×103×9.81×0.4 + 7.16×103=6.05×103Pa4. 本题附图为远距离测量控制装置，用以测定分相槽内煤油和水的两相界面位置。

第一章流体流动一、流体静力学：压强，密度，静力学方程二、流体基本方程：流速流量，连续性方程，伯努利方程三、流体流动现象：牛顿粘性定律，雷诺数，速度分布四、摩擦阻力损失：直管，局部，总阻力，当量直径五、流量的测定：测速管，孔板流量计，文丘里流量计六、离心泵：概述，特性曲线，气蚀现象和安装高度8■绝对压力：以绝对真空为基准测得的压力。

■表压/真空度 ：以大气压为基准测得的压力。

表 压 = 绝对压力 － 大气压力真空度 = 大气压力 － 绝对压力1.1流体静力学1.流体压力/压强表示方法绝对压力绝对压力绝对真空表压真空度1p 2p 大气压标准大气压：1atm = 1.013×105Pa =760mmHg =10.33m H 2O112.流体的密度Vm =ρ①单组分密度),(T p f =ρ■液体：密度仅随温度变化（极高压力除外），其变化关系可从手册中查得。

■气体：当压力不太高、温度不太低时，可按理想气体状态方程计算注意：手册中查得的气体密度均为一定压力与温度下之值，若条件不同，则需进行换算。

②混合物的密度■ 混合气体：各组分在混合前后质量不变，则有nn 2111m φρφρφρρ+++= RTpM m m=ρnn 2211m y M y M y M M +++= ■混合液体：假设各组分在混合前后体积不变，则有nmn12121w w w ρρρρ=+++①表达式—重力场中对液柱进行受力分析：液柱处于静止时，上述三力的合力为零:■下端面所受总压力 A p P 22=方向向上■上端面所受总压力 A p P 11=方向向下■液柱的重力)(21z z gA G -=ρ方向向下p 0p 2p 1z 1z 2G3.流体静力学基本方程式g z p g z p 2211+=+ρρ能量形式)(2112z z g p p -+=ρ压力形式②讨论：■适用范围：适用于重力场中静止、连续的同种不可压缩性流体；■物理意义：在同一静止流体中，处在不同位置流体的位能和静压能各不相同，但二者可以转换，其总和保持不变。

第一章: 流体流动流体流动是化工厂中最基本的现象。

在化工厂内，不论是待加工的原料或是已制成的产品，常以液态或气态存在。

各种工艺生产过程中，往往需要将液体或气体输送至设备内进行物理处理或化学反应，这就涉及到选用什么型式、多大功率的输送机械，如何确定管道直径及如何控制物料的流量、压强、温度等参数以保证操作或反应能正常进行，这些问题都与流体流动密切相关。

流体是液体和气体的统称。

流体具有流动性，其形状随容器的形状而变化。

液体有一定的液面，气体则否。

液体几乎不具压缩性，受热时体积膨胀的不显著，所以一般将液体视为不可压缩的流体。

与此相反，气体的压缩民很强，受热时体积膨胀很大，所以气体是可压缩的流体。

如果在操作过程中，气体的温度和压强改变很小，气体也可近似地按不可压缩流体来处理。

流体是由大量的不断作不规则运动的分子组成，各个分子之以及分子内部的原子之间均保留着一定的空隙，所以流体内部是不连续而存在空隙的，要从单个分子运动出发来研究整个流体平衡或运动的规律，是很困难而不现实。

所以在流体力学中，不研究个别分子的运动，只研究由大量分子组成的分子集团，设想整个流体由无数个分子集团组成，每个分子集团称为“质点”。

质点的大小与它所处的空间在、相比是微不足道的，但比分子自由程要大得多。

这样可以设想在流体的内部各个质点相互紧挨着，它们之间没有任何空隙而成为连续体。

用这种处理方法就可以不研究分子间的相互作用以及复杂的分子运动，主要研究流体的宏观运动规律，而把流体模化为连续介质，但不是所有情况都是如此的，高真空度下的气体就不能视为连续介质了。

液体和气体统称为流体。

流体的特征是具有流动性，即其抗剪和抗张的能力很小；无固定形状，随容器的状而变化；在外力作用下其内部发生相对运动。

化工生产的原料及产品大多数是流体。

在化工生产中，有以下几个主要方面经常要应用流体流动的基本原理及其流动规律：(1) 管内适宜流速、管径及输送设备的选定；(2) 压强、流速和流量的测量；(3) 传热、传质等过程中适宜的流动条件的确定及设备的强化。

化工原理–流体流动概述引言流体流动是化工领域中常见的一个研究领域，它在很多工艺过程中起着至关重要的作用。

流体流动的研究可以帮助我们了解流体在管道、设备和反应器中的行为，从而优化工艺过程，提高生产效率。

本文将从基本理论、流体流动模型和流动参数分析等方面对流体流动进行概述。

基本理论流体流动的基本理论是流体力学的一部分。

它研究流体在管道、设备和反应器中的运动规律。

在流体流动中，有两个重要的参数：流速和压力。

流速描述了流体在单位时间内通过某一截面的体积，通常以米/秒来表示。

压力则是单位面积上的力，通常以帕斯卡（Pa）来表示。

根据流速和压力的变化，可以描绘出流体的流动状态，理解流体在设备中的传输行为。

流体流动模型在化工过程中，流体流动的行为非常复杂，通常使用一些流体流动模型来描述。

常见的流体流动模型有层流流动和湍流流动。

层流流动层流流动是指流体在管道或设备中呈稳定的层流状态，流体在截面中的各个部分以均匀的速度运动。

在层流流动中，不同层之间的流速差很小，流体分子之间的相对位置一直保持不变。

层流流动通常发生在流速较低的条件下，管道的直径较小，并且流体的黏性较高。

层流流动可以用泊肃叶定律进行描述。

湍流流动湍流流动是指流体在管道或设备中呈不稳定的湍流状态，流体在截面中的各个部分以复杂而无规律的方式运动。

在湍流流动中，不同层之间的流速差很大，流体分子之间的相对位置不断变化。

湍流流动通常发生在流速较高的条件下，管道的直径较大，并且流体的黏性较低。

湍流流动的模型较为复杂，常用的描述方法有雷诺平均法和雷诺应力传递方程。

流动参数分析在对流体流动进行研究时，需要对一些流动参数进行分析。

这些参数可以帮助我们了解流体的流动特性和传输行为。

流量流量指的是单位时间内通过管道或设备截面的流体体积。

通常以单位时间内液体或气体通过单位面积的体积来表示，单位为立方米/秒。

流量是一个非常重要的参数，可以用来确定设备的尺寸和流程的设计。

压降压降指的是流体在通过管道或设备时由于阻力而导致的压力降低。

化工原理第一章流体流动第一章 流体流动一、流体流动的数学描述在化工生产中，经常遇到流体通过管道流动这一最基本的流体流动现象。

当流体在管内作稳定流动时，遵循两个基本衡算关系式，即质量衡算方程式和机械能衡算方程式。

质量衡算方程式在稳定的流动系统中，对某一划定体积而言，进入该体积的流体的质量流量等于流出该体积的质量流量。

如图1—1所示，若取截面1—1′、2—2′及两截面间管壁所围成的体积为划定体积，则ρρρuA A u A u ==222111 (1-1a)对不可压缩、均质流体(密度ρ＝常数)的圆管内流动，上式简化为2221211ud d u d u == (1-1b)机械能衡算方程式在没有外加功的情况下，流动系统中的流体总是从机械能较高处流向机械能较低处，两处机械能之差为流体克服流动阻力做功而消耗的机械能，以下简称为阻力损失。

如图1—1所示，截面1—1′与2—2′间单位质量流体的机械能衡算式为f 21w Et Et += (1-2)式中 221111u p gz Et ++=ρ，截面1—1′处单位质量流体的机械能，J ／kg ；222222u p gz Et ++=ρ，截面2—2′处单位质量流体的机械能，J ／kg ；∑⎥⎦⎤⎢⎣⎡∑+∑=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∑+=2)(222f u d l l u d l w e λζλ，单位质量流体在划定体积内流动时的总阻力损失，J ／kg 。

其中，λ为雷诺数Re 和相对粗糙度ε / d 的函数，即⎪⎪⎭⎫ ⎝⎛=d du εμρφλ,。

上述方程式中，若将Et 1、Et 2、w f 、λ视为中间变量，则有z 1、z 2、p 1、p 2、u 1、u 2、d 1、d 2、d 、u 、l 、∑ζ(或∑l e )、ε、ρ、μ等15个变量，而独立方程仅有式(1-1)(含两个独立方程)、式(1-2)三个。

因此，当被输送流体的物性(ρ，μ)已知时，为使方程组有唯一解，还需确定另外的10个变量，其余3个变量才能确定。