三角函数值表及记忆方法

30、 45、 60角的正弦值、余弦值、正切值的记忆法
1.口诀法：可用“一二三、三二一、三九二十七”来帮助记忆，如下表：
2.数形定义法：如右图，在含 30角的直角三角形中，三边的比为1︰3︰2，即 30角的对边（或 60角的邻边）为“1”，
60角的对边（或 30角的邻边）为“3”，斜边为“2”；再利用锐角三角函数的定义得到,213030sin ==斜边角的对边 ,233030cos ==斜边角的邻边
30tan =角的邻边角的对边 3030=33，同样可得 60角的三角函数值。

在等腰直角三角形中，三边的比为1︰1︰2，即 45角的对边或邻边都是“1”， 斜边是“
2”； 再由锐角三角函数的定义得,222
14545sin ===斜边角的对边 ,22214545cos ===斜边角的邻边 1454545tan ==角的邻边角的邻边 。

60 ︒
45 ︒ 45 ︒ 30 ︒ 2
1 1
2
3 1。

初中三角函数值口诀
在初中数学学习中，三角函数是一个重要的知识点，掌握
好三角函数的值可以帮助我们解决许多数学问题。

为了方便记忆，我们可以通过口诀的方式来记住三角函数的特定角度对应的值。

下面就给大家总结了一些常用的初中三角函数值口诀。

正弦函数值口诀
1.0°时正弦为0，小孩又又画零。

2.30°时是1，树仨三角肩。

3.45°里头比树唐，路上斜方根二，树根斜树根，两边
就是一。

4.60度栽草成。

余弦函数值口诀
1.0度余弦不动，短久饭店开，两个开。

2.30度开树三两只猴，树叶三十开开，斜树根。

3.45度是树的根，斜树根两边为一，从根连起。

4.60度是斜的石。

正切函数值口诀
1.0切相，零，十个开。

2.30度开，开，根。

3.45度斜，根，一，二。

4.60斜，开，根。

以上就是初中三角函数值口诀的内容，希望这些口诀可以
帮助大家记忆三角函数的值，更好地应用于数学问题的解答中。

愿大家在学习中取得更多的进步！。

常用三角函数公式及口诀三角函数是数学中非常重要的一部分，它经常在几何、物理、工程等各个领域中被广泛应用。

掌握常用的三角函数公式和口诀，将有助于我们更好地理解和应用它们。

下面是一些常用的三角函数公式及口诀：一、三角函数的定义：在一个直角三角形中，正弦(sin)定义为对边与斜边的比值，余弦(cos)定义为邻边与斜边的比值，正切(tan)定义为对边与邻边的比值。

即：sin(θ) = 对边 / 斜边cos(θ) = 邻边 / 斜边tan(θ) = 对边 / 邻边二、特殊角的三角函数值：1.30°角特殊值：sin(30°) = 1/2cos(30°) = √3/2tan(30°) = 1/√32.45°角特殊值：sin(45°) = √2/2cos(45°) = √2/2tan(45°) = 13.60°角特殊值：sin(60°) = √3/2cos(60°) = 1/2tan(60°) = √3三、基本三角函数的性质：1.正弦、余弦的周期性：sin(θ) = sin(θ + 2π)cos(θ) = cos(θ + 2π)2.正弦、余弦的对称性：sin(-θ) = -sin(θ)cos(-θ) = cos(θ)3.正弦、余弦的平方和为1：sin^2(θ) + cos^2(θ) = 14.正切的周期性：tan(θ) = tan(θ + π)四、和差角公式：1.正弦和差角公式：sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B) 2.余弦和差角公式：cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B)3.正切和差角公式：tan(A ± B) = (tan(A) ± tan(B)) / (1 ∓ tan(A)tan(B))五、倍角公式：1.正弦倍角公式：sin(2A) = 2sin(A)cos(A)2.余弦倍角公式：cos(2A) = cos^2(A) - sin^2(A) = 2cos^2(A) - 1 = 1 - 2sin^2(A) 3.正切倍角公式：tan(2A) = 2tan(A) / (1 - tan^2(A))六、半角公式：1.正弦半角公式：sin(A/2) = ±√[(1 - cos(A)) / 2]2.余弦半角公式：cos(A/2) = ±√[(1 + cos(A)) / 2]3.正切半角公式：tan(A/2) = ±√[(1 - cos(A)) / (1 + cos(A))]七、和差化积公式：1.正弦和差化积公式：sin(A) + sin(B) = 2sin[(A+B)/2]cos[(A-B)/2]sin(A) - sin(B) = 2cos[(A+B)/2]sin[(A-B)/2] 2.余弦和差化积公式：cos(A) + cos(B) = 2cos[(A+B)/2]cos[(A-B)/2]cos(A) - cos(B) = -2sin[(A+B)/2]sin[(A-B)/2]。

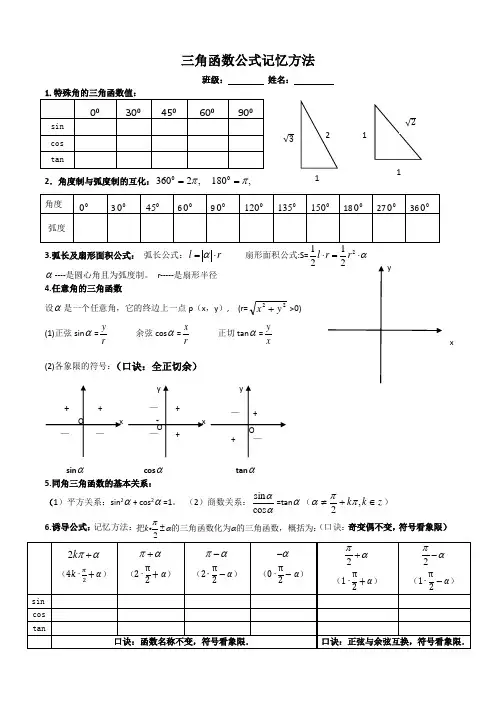
三角函数值怎么记忆口诀三角函数在数学中扮演着重要的角色，它们常常出现在各种数学问题中。

其中，正弦函数、余弦函数和正切函数是最常见的三角函数。

那么，我们如何记忆这些三角函数的数值呢？接下来，我们将介绍一些简单易记的口诀，帮助你轻松记忆三角函数的数值。

正弦函数Sin的数值正弦函数Sin的数值可以用“先生东”这个口诀来记忆。

具体来说，分别是：•Sin(0°) = 0•Sin(30°) = 1/2•Sin(45°) = 1/√2•Sin(60°) = √3/2•Sin(90°) = 1这里的口诀“先生东”可以帮助我们记忆正弦函数在经典角度下的数值。

余弦函数Cos的数值余弦函数Cos的数值可以用“酸奶泡”这个口诀来记忆。

具体来说，分别是：•Cos(0°) = 1•Cos(30°) = √3/2•Cos(45°) = 1/√2•Cos(60°) = 1/2•Cos(90°) = 0口诀“酸奶泡”可以帮助我们快速记忆余弦函数在经典角度下的数值。

正切函数Tan的数值正切函数Tan的数值可以用“斜起三分”口诀来记忆。

具体是：•Tan(0°) = 0•Tan(30°) = 1/√3•Tan(45°) = 1•Tan(60°) = √3•Tan(90°) = 无穷大口诀“斜起三分”可以帮助我们简单记住正切函数在常见角度下的数值。

通过以上口诀的记忆，我们可以轻松快速地记住正弦函数、余弦函数和正切函数在经典角度下的数值。

当然，在实际问题中，我们也可以通过计算器或者相关公式来求解三角函数的数值，但是通过口诀的记忆，可以在一些需要快速计算的场合发挥作用。

希望以上内容能帮助你更好地理解和记忆三角函数的数值。

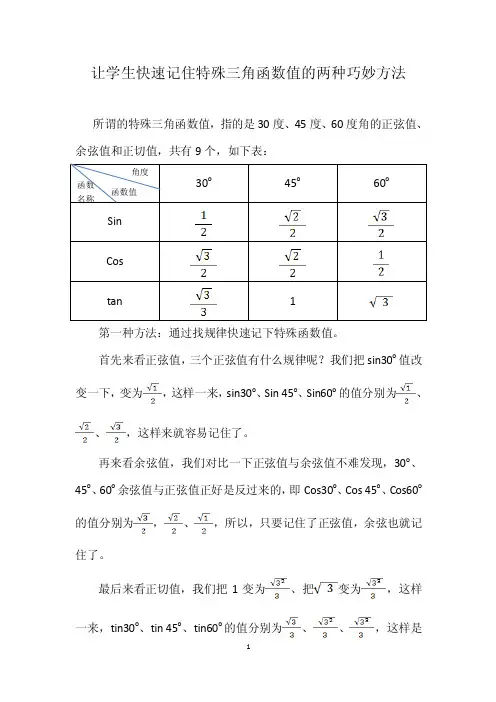
让学生快速记住特殊三角函数值的两种巧妙方法所谓的特殊三角函数值，指的是30度、45度、60度角的正弦值、余弦值和正切值，共有9个，如下表：第一种方法：通过找规律快速记下特殊函数值。

首先来看正弦值，三个正弦值有什么规律呢？我们把sin30o 值改变一下，变为，这样一来，sin30o 、Sin 45o 、Sin60o 的值分别为、、，这样来就容易记住了。

再来看余弦值，我们对比一下正弦值与余弦值不难发现，30o 、45o 、60o 余弦值与正弦值正好是反过来的，即Cos30o 、Cos 45o 、Cos60o 的值分别为，、，所以，只要记住了正弦值，余弦也就记住了。

最后来看正切值，我们把1变为、把变为，这样一来，tin30o 、tin 45o 、tin60o 的值分别为、、，这样是不是好记了？第二种方法：通过画图快速求出特殊三角函数值 首先画出第一幅图：有一个锐角为30度 的直角三角形ABC 。

如图：在Rt △ABC 中，∠A=30o ，∠C=90o 。

由已知条件得∠B=60o ，我们假设BC=1，根据“在直角三角形，30度角所对的直角边是斜边的一半”，所以得AB=2，在根据勾股定理求出AC=，所以sinA ＝sin30o ＝＝； sinB ＝sin60o ＝＝； cosA ＝cos30o ＝＝；cosB ＝cos60o ＝＝； tinA ＝tin30o ＝＝＝；tinB ＝tin60o ＝＝＝我们画出了第一幅图就把6个特殊函数值求了出来，接下来我在画第二幅图：有一个锐角为45度的直角三角形ABC 。

如图：在Rt △ABC 中，∠A=45o ，∠C=90o 。

由已知条件得∠B=45o ，我们假设BC=1，ABC BCA所以AC＝1，根据勾股定理得AB＝。

所以sinA＝sin45o＝＝；cosA＝cos45o＝＝；tinA＝tin45o＝＝＝1。

这样一来我们通过画两幅图就可以轻而易举的把9个特殊的三角函数值求出来了。

《三角函数》公式记忆表一、诱导公式：第一组：ααπsin )2sin(=+k ααπc o s )2c o s (=+k ααπt a n )2t a n (=+k 第二组：ααπsin )sin(-=+ ααπc o s )c o s (-=+ ααπt a n )t a n (=+ 第三组：ααπsin )sin(=- ααπc o s )c o s (-=- ααπt a n )t a n (-=- 第四组：ααsin )sin(-=- ααc o s )c o s (=- ααtan )tan(-=- 第五组：ααπsin )2sin(-=- ααπc o s )2c o s (=- ααπt a n )2t a n (-=- 二、同角三角函数的基本关系式：1、平方关系：1cos sin 22=+αα αα22s e c t a n 1=+ αα22c s c c o t 1=+2、商数关系：αααcos sin tan = 3、倒数关系：1csc sin =⋅αα 1s e c c o s =⋅αα 1c o t t a n =⋅αα三、互余公式： 第一组：ααπcos )2sin(=- ααπs i n )2c o s (=- ααπc o t )2t a n (=-第二组：ααπcos )2sin(=+ ααπs i n )2c o s (-=+ ααπc o t )2t a n (-=+ 第三组：ααπcos )23sin(-=- ααπs i n )23c o s (-=- ααπc o t )23t a n (=-第四组：ααπcos )23sin(-=+ ααπs i n )23c o s (=+ ααπc o t )23t a n (-=+四、两角和与差的三角函数：第一组：βαβαβαsin sin cos cos )cos(-=+ βαβαβαs i n c o s c o s s i n )s i n (+=+βαβαβαsin sin cos cos )cos(+=- βαβαβαs i n c o s c o s s i n )s i n (-=- 第二组：βαβαβαtan tan 1tan tan )tan(-+=+ βαβαβαt a n t a n 1t a n t a n )t a n (+-=-五、倍角公式αααcos sin 22sin = ααα2t a n 1t a n 22t a n-= 1cos 2sin 21sin cos 2cos 2222-=-=-=ααααα六、降次公式：22cos 1sin 2αα-=22cos 1cos 2αα+=七、半角公式：*2cos 12sinαα-±= 2cos 12cos αα+±= αααααααsin cos 1cos 1sin cos 1cos 12tan-=+=+-±=八、万能公式：*2tan 12tan2sin 2ααα+=2t a n12t a n 1c o s 22ααα+-=2tan 12tan2tan 2ααα-=九、和差化积公式：*2cos2sin2sin sin βαβαβα-+=+ 2s i n2c o s2s i n s i n βαβαβα-+=-2cos 2cos 2cos cos βαβαβα-+=+ 2s i n2s i n 2c o s c o s βαβαβα-+-=- 十、积化和差公式：*))sin()(sin(21cos sin βαβαβα-++=))sin()(sin(21sin cos βαβαβα--+= ))cos()(cos(21cos cos βαβαβα-++= ))cos()(cos(21sin sin βαβαβα--+-=十一、其它：1、与α角终边相同的角β的集合：}{z k k ∈+=,2απββ2、弧长公式与弧度公式：r l α= , rl=α l (是弧长，r 是半径) 3、0n 化为弧度等于180πn 弧度，α弧度等于0)180(πα。

三角函数值快速记忆方法
记忆三角函数值的方法有很多种，以下是几种常见的方法：
1. 利用特殊角的数值：记住0度、30度、45度、60度和90度的正弦、余弦和正切值。

例如，0度时，正弦值为0，余弦值为1，正切值为0，可以记为（0,1,0）；30度时，正弦值为1/2，余弦值为√3/2，正切值为√3/3，可以记为（1/2,√3/2,√3/3）。

2. 利用单位圆：将单位圆上各个角度对应的三角函数值进行记忆。

例如，单位圆上30度对应的点为（√3/2, 1/2），则可记住正弦值为1/2，余弦值为√3/2。

3. 利用三角函数的周期性：正弦函数和余弦函数的周期均为2π，可以利用周期性来记忆。

例如，sin(π/2)的值为1，那么sin(π/2+2π)的值也为1，sin(π/2+4π)的值也为1，以此类推。

4. 利用三角函数的性质：例如，正弦函数的值范围在-1到1之间，且在第一、二象限为正值，在第三、四象限为负值，可以利用这些性质来记忆三角函数值的正负情况。

无论采用哪种方法，都需要多加练习和记忆，通过不断的练习和复习，可以更加熟练地记忆三角函数值。

三角函数公式大全
一、定义
直
二、函数关系
倒数关系：；；
商数关系：；．
平方关系：；；
三、诱导公式
口诀：奇变偶不变，符号看象限
公式一：设为任意角，终边相同的角的同一三角函数的值相等：
公式二：设为任意角，与的三角函数值之间的关系：
公式三：任意角与的三角函数值之间的关系：
公式四：与的三角函数值之间的关系：
公式五：与的三角函数值之间的关系：
公式六：及与的三角函数值之间的关系：
四、基本公式
1.和差角公式
口诀：正余同余正，余余反正正
；
；
；
2.和差化积
口诀：正加正，正在前。

正减正，余在前。

余加余，余并肩。

余减余，余不见，负号很讨厌。

；
；
3.积化和差
4.倍角公式
sin4A=-4*(cosA*sinA*（2*sinA^2-1））
cos4A=1+(-8*cosA^2+8*cosA^4）
tan4A=（4*tanA-4*tanA^3）/（1-6*tanA^2+tanA^4）
5.半角公式
五、万能公式
六、辅助角公式
七、三角形定理
1.正弦定理
在任意△ABC中，角A、B、C所对的边长分别为a、b、c，三角形外接圆的半径为R．则有
正弦定理变形可得：
2.余弦定理
在如图所示的在△ABC中，有
或。