高一立体几何试卷及答案

高中数学立体几何测试试卷学校：___姓名：___班级：___考号：__一．单选题1．一个圆锥的侧面展开图的圆心角为90°，它的表面积为a，则它的底面积为（）A．B．C．D．2．设α为平面，m，n为直线（）A．若m，n与α所成角相等，则m∥nB．若m∥α，n∥α，则m∥nC．若m，n与α所成角互余，则m⊥nD．若m∥α，n⊥α，则m⊥n3．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（）A．75°B．60°C．45°D．30°4．设α是空间中的一个平面，l，m，n是三条不同的直线，①若m⊂α，n⊂α，l⊥m，l⊥n，则l⊥α；②若l∥m，m∥n，l⊥α，则n⊥α；③若l∥m，m⊥α，n⊥α，则l∥n；④若m⊂α，n⊥α，l⊥n，则l∥m；则上述命题中正确的是（）A．①②B．②③C．②④D．③④5．已知一个铜质的五棱柱的底面积为16cm2，高为4cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（）A．2cm B．C．4cm D．8cm6、在正方体ABCD-A l B1C1D1中，P是正方体的底面A l B1C1D1（包括边界）内的一动点（不与A1重合），Q是底面ABCD内一动点，线段A1C与线段PQ相交且互相平分，则使得四边形A1QCP面积最大的点P有（）A．1个B．2个C．3个D．无数个7．如图所示几个空间图形中，虚线、实线使用不正确的有（）A．②③B．①③C．③④D．④二．填空题8、如图，在四棱锥S-ABCD中，SB⊥底面ABCD．底面ABCD为梯形，AB⊥AD，AB∥CD，AB=1，AD=3，CD=2．若点E是线段AD上的动点，则满足∠SEC=90°的点E的个数是______．9、一个正方体的六个面上分别标有字母A、B、C、D、E、F，如图是此正方体的两种不同放置，则与D面相对的面上的字母是______．10．设α、β为互不重合的平面，m、n为互不重合的直线，下列四个命题中所有正确命题的序号是______．①若m⊥α，n⊂α，则m⊥n；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β．③若m∥α，n∥α，则m∥n．④若α⊥β，α∩β=m，n⊂α，n⊥m，则n⊥β．三．简答题11、在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，S D=，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F．（1）求证：四边形EFCD为直角梯形；（2）设SB的中点为M，当的值是多少时，能使△DMC为直角三角形？请给出证明．12、正三棱台的高为3，上、下底面边长分别为2和4，求这个棱台的侧棱长和斜高．13、已知三棱椎D-ABC，AB=AC=1，AD=2，∠BAD=∠CAD=∠BAC=90°，点E，F分别是BC，DE的中点，如图所示，（1）求证AF⊥BC（2）求线段AF的长．参考答案一．单选题1．一个圆锥的侧面展开图的圆心角为90°，它的表面积为a，则它的底面积为（）A．B．C．D．答案：A解析：解：设圆锥的母线为l，所以圆锥的底面周长为：，底面半径为：=，底面面积为：．圆锥的侧面积为：，所以圆锥的表面积为：+=a，底面面积为：=．故选A．2．设α为平面，m，n为直线（）A．若m，n与α所成角相等，则m∥nB．若m∥α，n∥α，则m∥nC．若m，n与α所成角互余，则m⊥nD．若m∥α，n⊥α，则m⊥n答案：D解析：解：对于选项A，若m，n与α所成角相等，m，n也可能相交、平行、异面；故A错误；对于选项B，若m∥α，n∥α，直线m，n也可能平行，也可能相交，还有可能异面；故B 错误；对于选项C，若m，n与α所成角互余，如与α所成角分别为30°和60°，直线m，n所成的角有可能为30°；故C错误；对于选项D，根据线面垂直的性质，容易得到m⊥n；故D正确；故选D．3．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（）A．75°B．60°C．45°D．30°答案：C解析：解析：如图，四棱锥P-ABCD中，过P作PO⊥平面ABCD于O，连接AO则AO是AP在底面ABCD上的射影．∴∠PAO即为所求线面角，∵AO=，PA=1，∴cos∠PAO==．∴∠PAO=45°，即所求线面角为45°．故选C．4．设α是空间中的一个平面，l，m，n是三条不同的直线，①若m⊂α，n⊂α，l⊥m，l⊥n，则l⊥α；②若l∥m，m∥n，l⊥α，则n⊥α；③若l∥m，m⊥α，n⊥α，则l∥n；④若m⊂α，n⊥α，l⊥n，则l∥m；则上述命题中正确的是（）A．①②B．②③C．②④D．③④答案：B解析：解：①根据线面垂直的判定，当m，n相交时，结论成立，故①不正确；②根据平行线的传递性，可得l∥n，故l⊥α时，一定有n⊥α，故②正确；③由垂直于同一平面的两直线平行得m∥n，再根据平行线的传递性，即可得l∥n，故③正确．④m⊂α，n⊥α，则n⊥m，∵l⊥n，∴可以选用正方体模型，可得l，m平行、相交、异面都有可能，如图所示，故④不正确故正确的命题是②③故选B．5．已知一个铜质的五棱柱的底面积为16cm2，高为4cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（）A．2cm B．C．4cm D．8cm答案：C解析：解：∵铜质的五棱柱的底面积为16cm2，高为4cm，∴铜质的五棱柱的体积V=16×4=64cm3，设熔化后铸成一个正方体的铜块的棱长为acm，则a3=64解得a=4cm故选C6、在正方体ABCD-A l B1C1D1中，P是正方体的底面A l B1C1D1（包括边界）内的一动点（不与A1重合），Q是底面ABCD内一动点，线段A1C与线段PQ相交且互相平分，则使得四边形A1QCP面积最大的点P有（）A．1个B．2个C．3个D．无数个答案：C解：∵线段A1C与线段PQ相交且互相平分，∴四边形A1QCP是平行四边形，因A l C的长为定值，为了使得四边形A1QCP面积最大，只须P到A l C的距离为最大即可，由正方体的特征可知，当点P位于B1、C1、D1时，平行四边形A1QCP面积相等，且最大．则使得四边形A1QCP面积最大的点P有3个．故选C．7．如图所示几个空间图形中，虚线、实线使用不正确的有（）A．②③B．①③C．③④D．④答案：D解析：解：根据棱柱的放置和“看见的棱用实线、看不见的棱用虚线”，则①②③正确，④错误，故选D．二．填空题8、如图，在四棱锥S-ABCD中，SB⊥底面ABCD．底面ABCD为梯形，AB⊥AD，AB∥CD，AB=1，AD=3，CD=2．若点E是线段AD上的动点，则满足∠SEC=90°的点E的个数是______．答案：2解：连接BE，则∵SB⊥底面ABCD，∠SEC=90°，∴BE⊥CE．故问题转化为在梯形ABCD中，点E是线段AD上的动点，求满足BE⊥CE的点E的个数．设AE=x，则DE=3-x，∵AB⊥AD，AB∥CD，AB=1，AD=3，CD=2，∴10=1+x2+4+（3-x）2，∴x2-3x+2=0，∴x=1或2，∴满足BE⊥CE的点E的个数为2，∴满足∠SEC=90°的点E的个数是2．故答案为：2．9、一个正方体的六个面上分别标有字母A、B、C、D、E、F，如图是此正方体的两种不同放置，则与D面相对的面上的字母是______．答案：B解析：解：由此正方体的两种不同放置可知：与C相对的是F，因此D与B相对．故答案为：B．10．设α、β为互不重合的平面，m、n为互不重合的直线，下列四个命题中所有正确命题的序号是______．①若m⊥α，n⊂α，则m⊥n；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β．③若m∥α，n∥α，则m∥n．④若α⊥β，α∩β=m，n⊂α，n⊥m，则n⊥β．答案：①④解析：解：①若m⊥α，n⊂α，利用线面垂直的性质，可得m⊥n，正确；②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；两条相交直线才行，不正确．③m∥α，n∥α，则m与n可能平行、相交、异面，不正确．④若α⊥β，α∩β=m，n⊂α，n⊥m，则由面面垂直的性质定理我们易得到n⊥β，正确．故答案为：①④．三．简答题11、在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，S D=，在线段SA上取一点E（不含端点）使EC=AC，截面CDE与SB交于点F．（1）求证：四边形EFCD为直角梯形；（2）设SB的中点为M，当的值是多少时，能使△DMC为直角三角形？请给出证明．答案：解：（1）∵CD∥AB，AB⊂平面SAB，∴CD∥平面SAB面EFCD∩面SAB=EF，∴CD∥EF．∵∠D=90°，∴CD⊥AD，又SD⊥面ABCD，∴SD⊥CD，∴CD⊥平面SAD，∴CD⊥ED又EF＜AB＜CD，∴EFCD为直角梯形．（2）当=2时，能使DM⊥MC．∵AB=a，∴，∴，∴SD⊥平面ABCD，∴SD⊥BC，∴BC⊥平面SBD．在△SBD中，SD=DB，M为SB中点，∴MD⊥SB．∴MD⊥平面SBC，MC⊂平面SBC，∴MD⊥MC，∴△DMC为直角三角形．12、正三棱台的高为3，上、下底面边长分别为2和4，求这个棱台的侧棱长和斜高．答案：解：如图所示，正三棱台ABC-A1B1C1中，高OO1=3，底面边长为A1B1=2，AB=4，∴OA=×AB=，O1A1=×A1B1=，∴棱台的侧棱长为AA1==；又OE=×AB=，O1E1=×A1B1=，∴该棱台的斜高为EE1==．13、已知三棱椎D-ABC，AB=AC=1，AD=2，∠BAD=∠CAD=∠BAC=90°，点E，F分别是BC，DE的中点，如图所示，（1）求证AF⊥BC（2）求线段AF的长．答案：解：（1）分别以AB、AC和AD为x、y、z轴，建立空间直角坐标系O-xyz，如图所示：记A（0，0，0），B（1，0，0），C（0，1，0），D（0，0，2），∴E（，，0），F（，，1）；∴（，，1），=（-1，1，0），∴•=×（-1）+×1+1×0=0，∴⊥，即AF⊥BC；（2）∵=（，，1），∴||===，即线段AB=．。

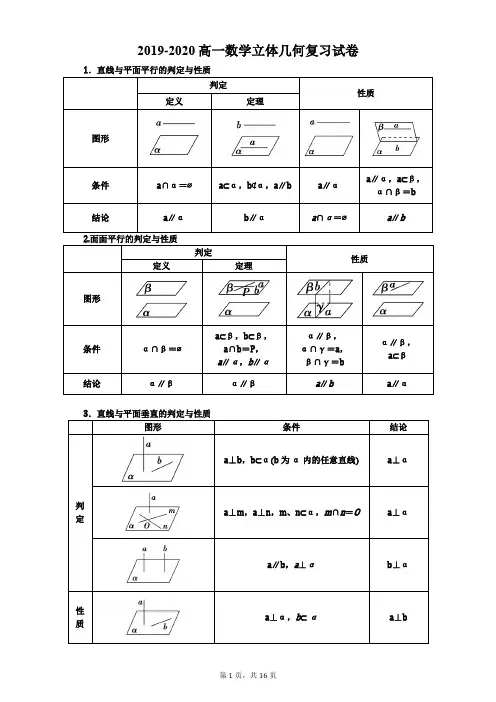
2019-2020高一数学立体几何复习试卷定义定理图形(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条斜线和这个平面所成的角．(2)线面角θ的范围：θ∈]2,0[π.6．二面角的有关概念(1)二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．(2)二面角的平面角：过二面角棱上的一点，在两个半平面内分别作与棱垂直的射线，则两射线所成的角叫做二面角的平面角.（二）考点剖析题型一：定理与性质的判断1. 设α，β，γ为两两不重合的平面，l ，m ，n 为两两不重合的直线，给出下列四个命题：①若α⊥γ，β⊥γ，则α//β；②若m ⊂α，n ⊂α，m//β，n//β，则α//β； ③若α//β，l ⊂α，则l//β；④若α∩β=l ，β∩γ=m ，γ∩α=n ，l//γ，则m//n ． 其中真命题的个数是( ) A. 1 B. 2 C. 3 D. 4 2. 下列命题错误的是( )A. 不在同一直线上的三点确定一个平面B. 两两相交且不共点的三条直线确定一个平面C. 如果两个平面垂直，那么其中一个平面内的直线一定垂直于另一个平面D. 如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面3.设m、n是两条不同的直线，α、β为两个不同的平面，则下列四个命题中不正确的是()A. m⊥α，n⊥β且α⊥β，则m⊥nB. m⊥α，n//β且α//β，则m⊥nC. m//α，n⊥β且α⊥β，则m//nD. m⊥α，n⊥β且α//β，则m//n4.设l为直线，α,β是两个不同的平面，下列命题中正确的是()A.若l//α，l//β，则α//βB. 若l⊥α，l⊥β，则α//βC. 若l⊥α，l//β，则α//βD. 若α⊥β，l//α，则l⊥β题型二：异面直线5.如图所示，在正方体ABCD−A1B1C1D1中，O是底面正方形ABCD的中心，M是D1D的中点，N是A1B1的中点，则直线NO，AM的位置关系是()A. 平行B. 相交C. 异面且垂直D. 异面不垂直6.如图，三棱柱ABC−A 1B1C1中，侧棱AA1⊥底面A1B1C1，△A1B1C1是正三角形，E是BC中点，则下列叙述正确的是()A. CC1与B1E是异面直线B. AE，B1C1为异面直线，且AE⊥B1C1C. AC⊥平面ABB1A1D. A1C1//平面AB1E7.如图所示，在正方体ABCD—A 1B1C1D1中，E，F分别是AB1，BC1的中点，则异面直线EF与C1D所成的角为()A.30°B. 45°C. 60°D. 90°题型三：表面积与体积8.某简单几何体的三视图(俯视图为等边三角形)如图所示(单位：cm)，则该几何体的体积(单位：cm3)为()A. 18B. 6√3C. 3√3D. 2√39.某三棱锥的三视图如图所示(单位：cm)，则该三棱锥的表面积(单位：cm2)是()A.16B. 32C. 44D. 6410.如图，在圆锥SO中，O是底面圆的圆心，AB为一条直径，且AB=4，SA=4，C为SB的中点，则在圆锥SO的侧面上，从点A到点C 的最短路径为()A. 2√2B. 4C. 2√5D. 2√6题型四：线面、面面平行的判定及性质11.如图，在四棱锥P−ABCD中，PA⊥平面ABCD，底面ABCD是菱形，∠BAD=π，3 AB=2，PC=2√7，E，F分别是棱PC，AB的中点．(1)证明：EF//平面PAD；(2)求三棱锥C−AEF的体积．12.如图，在四棱锥P−ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．求证：(1)PA//平面EDB；(2)DE⊥平面PBC．13.如图所示，在三棱柱ABC−A1B1C1中H是A1C1的中点，D1，D分别为B1C1，BC的中点，，求证：(1)求证：HD//平面A1B1BA.(见图1)(2求证：平面A 1BD1//平面AC1D.(图2)14.如图，在多面体ABCDEF中，四边形ABCD是正方形，BF⊥平面ABCD，DE⊥平面ABCD，BF=DE，M为棱AE的中点．(1)求证：平面BDM//平面EFC;(2)若AB=1，BF=2，求三棱锥A−CEF的体积．15.如图，在长方体ABCD−A1B1C1D1中，E,F,G分别是AD,AB,C1D1的中点，求证：(1)平面D1EF//平面BDG；(2)若AB=BB1=1，BC=2，P为BC的中点，求异面直线BC1与FP所成角的余弦值．题型五：线面、面面垂直的判定与性质16.如图，在四棱锥P−ABCD中，底面ABCD是矩形，PA⊥平面ABCD，且PA=AD=2，AB=3，点E为线段PD的中点．(1)求证：AE⊥PC；(2)求三棱锥P−ACE的体积．17.如图所示，在四棱锥P−ABCD中，AD⊥AB，AD//BC，△PDA，△PAB都是边长为1的正三角形．(1)证明：平面PDB⊥平面ABCD；(2)求点C到平面PAD的距离．18.如图，三棱锥P−ABC中，点D，E分别为AB，BC的中点，且平面PDE⊥平面ABC．(1)求证：AC//平面PDE；(2)若PD=AC=2，PE=√3，求证：平面PBC⊥平面ABC．题型六：线面夹角与二面角19.如图，在四棱锥P−ABCD中PA⊥底面ABCD，∠DAB为直角，AB//CD，AD=CD=2AB=2PA=2，E,F分别为PC,CD的中点．(1)试证：CD⊥平面BEF；(2)求BC与平面BEF所成角的大小；(3)求三棱锥P−DBE的体积．20.如图，在四棱锥P−ABCD中，PD⊥平面ABCD，PD=2，DC=BC=1，AB=2，AB//DC，∠BCD=90°．(1)求证：AD⊥PB；(2)求平面DAP与平面BPC所成锐二面角的余弦值．21.如图，直三棱柱ABC−A1B1C1中，AB⊥AC,AB=1,AC=2,AA1=2,D,E分别为BC,A1C1的中点．(1)证明：C 1D//平面ABE;(2)求CC1与平面ABE所成角的正弦值．22.如图，在五边形ABCDE中，AB⊥BC，AE//BC//FD，F为AB的中点，AB=FD=2BC=2AE.现把此五边形ABCDE沿FD折成一个60∘的二面角．(1)求证：直线CE//平面ABF；(2)求二面角E−CD−F的平面角的余弦值．2019-2020高一数学立体几何复习试卷答案1.【答案】B【解答】解：①中α⊥γ，β⊥γ，则α与β相交或α//β，故①不正确； ②不正确，α与β有可能相交； ③正确；④中利用线面平行的性质定理可知其正确．2.解：由公理3可得，不在同一直线上的三点确定一个平面，故A 正确；由公理3和公理1可得，两两相交且不共点的三条直线确定一个平面，故B 正确； 由面面垂直的性质定理可得，如果两个平面垂直，那么其中一个平面内的直线若与交线垂直，则垂直于另一个平面，故C 错误；由面面平行的性质可得，如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面，故D 正确． 故选：C ．3.解：A ，分别垂直于两个垂直的平面的两条直线一定垂直，故该命题正确； B ，由m ⊥α，α//β可得出m ⊥β，再由n//β可得出m ⊥n ，故该命题正确；C ，m//α，n ⊥β且α⊥β成立时，m ，n 两直线的关系可能是相交、平行、异面，故该命题错误；D ，n ⊥β且α//β，可得出n ⊥α，再由m ⊥α，可得出m//n ，故该命题正确． 故选C ．4.解：对于A 项，在长方体中，任何一条棱都有和它相对的两个平面平行，但这两个平面相交，所以A 不对；对于B 项，若l ⊥α，l ⊥β，由线面垂直的性质可得α//β ，故B 正确；对于C 项，l ⊥α，l//β，由线面平行的性质可得β内存在一直线m ，使得l//m ，再由线面垂直的判定定理得m ⊥α，从而由面面垂直的判定定理得α⊥β，所以C 不对； 对于D 项，在长方体中，令下底面为β，左边侧面为α，此时α⊥β，在右边侧面中取一条对角线l ，则l//α，但l 与β不垂直，故D 不对； 故选B ． 5.【答案】C【解答】解：建立如图所示的空间直角坐标系，连接BD ， 设正方体的棱长为2，则A(2,0，0)，M(0,0，1)，O(1,1，0)，N(2,1，2)，则NO ⃗⃗⃗⃗⃗⃗ =(−1,0，−2)，AM ⃗⃗⃗⃗⃗⃗ =(−2,0，1)，NO ⃗⃗⃗⃗⃗⃗ ⋅AM ⃗⃗⃗⃗⃗⃗ =0， 易知直线NO ，AM 不相交，所以直线NO ，AM 的位置关系是异面且垂直， 故选C ．6.【答案】B解：由三棱柱ABCA 1B 1C 1中，侧棱AA 1垂直底面A 1B 1C 1， 底面三角形A 1B 1C 1是正三角形，E 是BC 中点，知：在A 中，因为CC 1与B 1E 在同一个侧面中，故CC 1与B 1E 不是异面直线，故A 错误；在B 中，因为AE ，B 1C 1为在两个平行平面中且不平行的两条直线，故它们是异面直线，又底面三角形A 1B 1C 1是正三角形，E 是BC 中点，故AE ⊥B 1C 1，故B 正确；在C 中，由题意知，上底面ABC 是一个正三角形，故不可能存在AC ⊥平面ABB 1A 1，故C 错误；在D 中，因为A 1C 1所在的平面与平面AB 1E 相交，且A 1C 1与交线有公共点，故A 1C 1//平面AB 1E 不正确，故D 错误．故选B ．7.【答案】C解：如下图：连接A1C1，A1D．取A1B1、B1C1的中点分别为G、H，连接EG、GH、HF，则GH//A1C1．因为E，F分别是AB1，BC1的中点，所以GE=//12A1A，HF=//12B1B，而ABCD−A1B1C1D1是正方体，因此GE=//HF，即四边形GEFH是平行四边形，所以EF//GH，因此EF//A1C1，所以异面直线EF与C1D所成的角就是直线A1C1与C1D所成的角(或补角)，即∠A1C1D．又因为ABCD−A1B1C1D1是正方体，所以ΔA1C1D是正三角形，因此∠A1C1D=60°，即异面直线EF与C1D所成的角为60°．故选C．8.【答案】C解：由题意可知几何体是底面为正三角形的三棱柱，底面边长为2，高为3，所以几何体的体积为：√34×22×3=3√3．故选C．9.【答案】B解：根据三视图知：该几何体是三棱锥，底面是直角三角形，PA⊥平面ABCD，BC⊂平面ABCD，∴PA⊥BC，又AC⊥BC，PA，AC⊂平面PAC，PA∩AC=A，∴BC⊥平面PAC，又PC⊂平面PAC，∴BC⊥PC，∴该几何体的表面积为S=12×(3×4+5×4+3×4+4×5)=32，故选B．10.【答案】C解：由题得圆锥底面圆半径为2，将圆锥的侧面展开得到一个扇形，连接AC，则AC即A到C的最短路径．扇形中弧AB的长为2π，∠ASB=2π4=π2，则AC=√SA2+SC2=√42+22=2√5．故选C．11.【答案】(1)证明：如图，取PD中点为G，连结EG，AG，则EG//CD，EG=12CD，AF//CD，AF=12CD，所以EG与AF平行并且相等，所以四边形AGEF是平行四边形，所以EF//AG，AG⊂平面PAD，EF⊄平面PAD.所以EF//平面PAD．(2)连结AC，BD交于点O，连结EO，因为E为PC的中点，所以EO为△PAC的中位线，又因为PA⊥平面ABCD，所以EO⊥平面ABCD，即EO为三棱锥E−AFC的高．在菱形ABCD中可求得AC=2√3，在Rt△PAC中，PC=2√7，所以PA=√PC2−AC2=4，EO=2，所以S▵ACF=12S▵ABC=12×12×AB×BCsin∠ABC=√32，所以V C−AEF=V E−ACF=13S▵ACF×EO=13×√32×2=√33．12.【答案】证明：(1)连接AC交BD于O，连接OE.∵E是PC的中点，O是AC的中点，∴PA//EO，又PA⊄平面BED，EO⊂平面BED，∴PA//平面BED.(2)∵侧棱PD⊥底面ABCD，BC⊂底面ABCD，∴PD⊥BC，∵底面ABCD是矩形，∴DC⊥BC，∵PD∩DC=D，PD⊂平面PDC，DC⊂平面PDC，∴BC⊥平面PDC，又DE⊂平面PDC，∴BC⊥DE，∵PD=DC，E是PC的中点．∴DE⊥PC，∵BC∩PC=C，BC⊂平面PBC，PC⊂平面PBC，∴DE⊥平面PBC．13.【答案】证明：(1)如图所示，连接HD，A1B，∵D为BC1的中点，H为A1C1的中点，∴HD//A1B.又HD⊄平面A1B1BA，A1B⊂平面A1B1BA，∴HD//平面A1B1BA．(2)如图所示，连接A1C交AC1于点M，∵四边形A1ACC1是平行四边形，∴M是A1C的中点，连接MD，∵D为BC的中点，∴A1B//DM．∵A1B⊂平面A1BD1，DM⊄平面A1BD1，∴DM//平面A1BD1，又由三棱柱的性质知，D1C1綊BD，∴四边形BDC1D1为平行四边形，∴DC1//BD1．又DC1⊄平面A1BD1，BD1⊂平面A1BD1，∴DC1//平面A1BD1．又∵DC1∩DM=D，DC1，DM⊂平面AC1D，∴平面A1BD1//平面AC1D.14.【答案】(1)证明：如图，设AC与BD交于点N，则N为AC的中点，连结MN，又M为棱AE的中点，∴MN//EC．∵MN⊄平面EFC，EC⊂平面EFC，∴MN//平面EFC．∵BF⊥平面ABCD，DE⊥平面ABCD，且BF=DE，∴BF//DE且BF=DE，∴四边形BDEF为平行四边形，∴BD//EF．∵BD⊄平面EFC，EF⊂平面EFC，∴BD//平面EFC．又MN∩BD=N，MN，BD⊂平面BDM，∴平面BDM//平面EFC．(2)连结EN，FN．在正方形ABCD中，AC⊥BD，又BF⊥平面ABCD，∴BF⊥AC．又BF∩BD=B，BF，BD⊂平面BDEF，∴AC⊥平面BDEF，又N是AC的中点，∴V三棱锥A−NEF =V三棱锥C−NEF，∴V三棱锥A−CEF =2V三棱锥A−NEF=2×13×AN×S△NEF=2×13×√22×12×√2×2=23，∴三棱锥A−CEF的体积为23．15.【答案】(1)证明：∵E，F分别是DA，AB的中点，∴EF//BD，又EF不在平面BDG内，∴EF//平面BDG，∵D1G//FB，且D1G=FB，∴四边形D1GBF是平行四边形，则D1F//GB，又D1F不在平面BDG内，GB⊂平面BDG，∴D1F//平面BDG，∴EF∩D1F=F，∴平面D1EF//平面BDG;(2)解：连接AC，AD1，∵F，P分别是AB，BC的中点，∴AC//FP，∵D 1C 1//DC ，DC//AB ，∴D 1C 1//AB ，∵D 1C 1=DC ，DC =AB ，∴D 1C 1=AB ，∴AD 1C 1B 是平行四边形，∴AD 1//BC 1，∠D 1AC(或其补角)为所求角， ∴AC =√5， AD =√5，CD 1=√2．16.【答案】解：(1)证明：∵PA ⊥平面ABCD ，∴PA ⊥CD ，又在矩形ABCD 中，CD ⊥AD ，∴CD ⊥平面PAD ，∵AE ⊂平面PAD ，∴CD ⊥AE ，又∵PA =AD ，E 为PD 中点，∴AE ⊥PD ，∴AE ⊥平面PCD ，∴AE ⊥PC ；(2)∵点E 为线段PD 的中点．∴V P−ACE =V E−PAC =12V P−ACD =12×13×2×12×2×3=1．17.【答案】解析：(1)证明：∵△PAB ，△PAD 都是正三角形， ∴AD =AB =PD =PB =1．设O 为BD 的中点，连接AO ，PO ，如图，∴PO ⊥BD ，AO ⊥BD ．在Rt △ADB 中，AD =AB =1，∴BD =√2．∵O 为BD 的中点，∴OA =12BD =√22． 在等腰△PDB 中，PD =PB =1，BD =√2，∴PO =√22． 在△POA 中，PO =√22，OA =√22，PA =1， ∴PO 2+OA 2=PA 2，∴PO ⊥OA ．又∵BD ∩OA =O ，BD ，OA ⊂平面ABCD ，∴PO ⊥平面ABCD ．又∵PO ⊂平面PDB ，∴平面PDB ⊥平面ABCD ．(2)由(1)知PO ⊥平面ABCD ，且PO =√22．设点C到平面PAD的距离为d，则V C−PAD=V P−ACD，即13SΔPAD⋅d=13SΔCAD⋅PO，所以√34⋅d=12×1×1×√22，解得d=√63，∴点C到平面PAD的距离为√63．18.【答案】证明：(1)因为点D，E分别为AB，BC的中点，所以DE为△ABC的中位线，所以DE//AC．因为AC⊄平面PDE，DE⊂平面PDE，所以AC//平面PDE．(2)因为点D，E分别为AB，BC的中点，所以DE=12AC．又因为AC=2，所以DE=1，因为PD=2，PE=√3，所以PD2=PE2+DE2，因此在△PDE中，PE⊥DE．又平面PDE⊥平面ABC，且平面PDE∩平面ABC=DE，PE⊂平面PDE，所以PE⊥平面ABC，又因为PE⊂平面PBC，所以平面PBC⊥平面ABC．19.【答案】(1)证明：∵AB//CD，CD=2AB，F为CD的中点，∴四边形ABFD为平行四边形，又∠DAB为直角，∴四边形ABFD为矩形，∴DC⊥BF，DC⊥AD，又PA⊥底面ABCD，CD⊂平面ABCD，∴DC⊥PA，∵PA⊂平面PAD，AD⊂平面PAD，且PA∩AD=A，∴DC⊥平面PAD，又PD⊂平面PAD，∴DC⊥PD，在△PCD内，E、F分别是PC、CD的中点，∴EF//PD，∴DC⊥EF，又EF∩BF=F，EF，BF⊂平面BEF由此得CD⊥平面BEF．(2)解：由(1)知，DC⊥平面BEF，则∠CBF 为BC 与平面BEF 所成角，在Rt △BFC 中，BF =AD =2，CF =12CD =1， ∴tan∠CBF =12， 则BC 与平面BEF 所成角的大小为． (3)由(1)知，CD ⊥平面PAD ，则平面PDC ⊥平面PAD ， 在Rt △PAD 中，设A 到PD 的距离为h ，即A 到平面PCD 的距离为h ， 则PA ·AD =PD ·ℎ，得ℎ=PA⋅ADPD =2√5=2√55， ∴A 到平面PDC 的距离为2√55， ∵AB//CD ，，∴AB//平面PCD ，即A 、B 到平面PCD 的距离相等，∴B 到平面PDC 的距离为2√55， ∵E 是PC 的中点，∴S △PDE =12S △PDC =12×√5×22=√52， ∴V P−DBE =V B−PDE =13×√52×2√55=13． 20.【答案】解：(1)在四边形ABCD 中，连接BD ，由DC =BC =1，AB =2，，在△ABD 中，BD =AD =√2，又AB =2，因此AD ⊥BD ，又PD ⊥面ABCD ，AD ⊂面ABCD ，∴PD ⊥AD ，PD ∩BD =D,PD,BD ⊂面PBD ，从而AD ⊥面PBD ． 而PB ⊂面PBD ∴AD ⊥PB ．(2)延长BC 和AD 交于点E ，连接PE ，又AB 平行于CD ，则CE =BC =1，DE =AD =√2．过C 点作CM ⊥PE 交于PE 上一点M ，过C 作CH ⊥面PDE 于点H ， 则∠CMH 为二面角C −PE −D 的平面角α．在直角三角形PCE 中，CM =1×√5√6． 又V C−PDE =V P−DCE ，12×(12×1×1)=CH ·(12×2×√2)，CH =√22． sinα=CH CM =√155,cosα=√105, 所求二面角的余弦值为√105． 21.【答案】证明：(1)取AB 中点H ，连接EH,HD ，在直三棱柱ABC −A 1B 1C 1中，EC 1//__12AC ．∵D 为BC 中点，H 为AB 中点，∴HD //̲̲̲12AC, HD //̲̲̲EC 1，∴四边形DHEC 1为平行四边形，∴DC 1//HE.∵EH ⊂平面ABE ，C 1D ⊈平面ABE ，∴C 1D//平面ABE ．(2)直三棱柱ABC −A 1B 1C 1中，AA 1⊥平面ABC ，∴AA 1⊥AB ． 又∵AB ⊥AC ，且AC ∩AA 1=A ，∴AB ⊥平面ACC 1A 1．过A 1作A 1F ⊥AE 于F.∵A 1F ⊂平面ACC 1A 1，∴AB ⊥A 1F ．又AB ∩AE =A, ∴A 1F ⊥平面ABE ．又CC 1//AA 1, ∴∠A 1AE 即为CC 1与平面ABE 所成的角．∵AA 1=2, A 1E =1, ∴AE =√5, ∴sin∠A 1AE =1√5=√55． 22.【答案】解：(Ⅰ)证明：∵AE//DF ，BC//FD ，∴AE//BC ， 又∵BC =AE ，∴四边形ABCE 为平行四边形，∴CE//AB ．又因为CE ⊄平面ABF ，AB ⊂平面ABF ，所以直线CE//平面ABF ；(Ⅱ)解：如图，取FD 得中点G ，连接EG 、CG ，在△CEG 中，作EH ⊥CG ，垂足为H ，在平面BCDF 中，作HI ⊥CD ，垂足为I ，连接EI ．∵AE =FG =BC ，AE//FG//BC ，∴AF//EG ，BF//CG ．又因为DF ⊥AF ，DF ⊥BF ，故DF ⊥平面ABF ，所以DF ⊥平面ECG ， ∵EH ⊥CG ，DF ⊥EH ，∴EH ⊥平面CGD ，∴EH ⊥CD ，又∵HI ⊥CD ，∴CD ⊥平面EHI ，所以CD ⊥EI ，从而∠EIH 为二面角E −CD −F 的平面角．设BC =AE =1，则FG =GD =CG =GE =1，由于∠EGC 为二面角C −FD −E 的平面角，即∠EGC =60°，所以在△CEG 中，HG =CH =12，EH =√32，HI =CHsin45°=√24， 所以EI =√144，所以cos∠EIH =√77．。

高一数学（必修二）立体几何初步单元测试卷及答案一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.如图所示，己知正方形O A B C ''''的边长为1，它是水平放置的一个平面图形的直观图，则其原图形的周长为( )A.8B.22C.4D.223+2.下列说法正确的是( ) A.三点确定一个平面B.圆心和圆上两个点确定一个平面C.如果两个平面相交有一个交点，则必有无数个公共点D.如果两条直线没有交点，则这两条直线平行3.正方体1111ABCD A B C D -中，P ，Q ，R 分别是AB ，AD ，11B C 的中点，那么正方体中过P ，Q ，R 的截面图形是( ) A.三角形B.四边形C.五边形D.六边形4.某圆柱的高为2，其正视图如图所示，圆柱上下底面圆周及侧面上的点A ，B ，D ，F ，C 在正视图中分别对应点A ，B ，E ，F ，C ，且3AE EF =，2BF BC =，异面直线AB ，CD 所成角的正弦值为45，则该圆柱的外接球的表面积为( )A.20πB.16πC.12πD.10π5.在《九章算术·商功》中将正四面形棱台体（棱台的上、下底面均为正方形）称为方亭.在方亭1111ABCD A B C D -中，1124AB A B ==，四个侧面均为全等的等腰梯形且面积之和为122( ) 282B.283142D.1436.异面直线是指( ) A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线7.如图，在正方体1111ABCD A B C D -中，E ，F 分别是11A D ，11B C 的中点，则与直线CF 互为异面直线的是( )A.1CCB.11B CC.DED.AE8.下列说法中正确的是( ) A.三点确定一个平面 B.四边形一定是平面图形 C.梯形一定是平面图形D.两个不同平面α和β有不在同一条直线上的三个公共点二、多选题（本题共4小题，每小题5分，共20分。

1、一个正方体的六个面分别写着1至6这六个数字，现将其任意投掷，出现的数字恰好为偶数的概率是？A、1/6B、1/3C、1/2D、2/3（答案：C。

解析：正方体有6个面，分别写着1至6，其中偶数有2、4、6，共3个面，所以出现偶数的概率为3/6=1/2。

）2、若一个长方体的长、宽、高分别为3cm、4cm、5cm，则其体积为？A、30cm³B、40cm³C、50cm³D、60cm³（答案：D。

解析：长方体的体积计算公式为长×宽×高，所以体积为3cm×4cm×5cm=60cm³。

）3、下列图形中，一定为平面图形的是？A、三角形B、平行四边形C、梯形D、圆（答案：A。

解析：三角形三个点共面，所以一定是平面图形。

平行四边形、梯形、圆在三维空间中可能不共面，因此不一定是平面图形。

）4、一个圆锥的底面半径为3cm，高为4cm，则其侧面积为？A、12π cm²B、15π cm²C、18π cm²D、20π cm²（答案：B。

解析：圆锥侧面积公式为πrl，其中r为底面半径，l为母线长。

母线长l可通过勾股定理求得，l=√(r²+h²)=√(3²+4²)=5cm，所以侧面积为π×3cm×5cm=15π cm²。

）5、一个球体的半径为R，则其表面积与体积的比值为？A、2/RB、3/RC、4/RD、6/R（答案：B。

解析：球的表面积公式为4πR²，体积公式为(4/3)πR³，所以表面积与体积的比值为(4πR²)/((4/3)πR³)=3/R。

）6、一个正方体的内切球半径为r，则该正方体的棱长为？A、rB、2rC、3rD、4r（答案：B。

解析：正方体的内切球半径等于正方体棱长的一半，所以棱长为2r。

立体几何试题一．选择题（每题 4 分，共 40 分）1. 已知 AB3003001500空间，下列命题正确的个数为（）（1）有两组对边相等的四边形是平行四边形, （2）四边相等的四边形是菱形（4）有两边及其夹角对应相等的两个三角（3）平行于同一条直线的两条直线平行 ;形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行，那么这条直线与另一个平面的位置关系是（）A平行B相交C在平面内D平行或在平面内4. 已知直线 m过平面外一点，作与平行的平面，则这样的平面可作（）A 1 个或 2 个B 0个或1个C1个 D 0个6.如图 , 如果 MC 菱形 ABCD 所在平面 , 那么 MA与 BD的位置关系是 ( )A平行B垂直相交C异面D相交但不垂直7. 经过平面外一点和平面内一点与平面垂直的平面有（）A 0 个B 1个C无数个 D 1个或无数个8.下列条件中 , 能判断两个平面平行的是 ( )B一个平面内的两条直线平行于另一个平面C一个平面内有无数条直线平行于另一个平面D一个平面内任何一条直线都平行于另一个平面9. 对于直线m ,n 和平面,, 使成立的一个条件是 ( )A m // n, n, mB m // n, n,mC m n,I m, nD m n, m //, n //)10 . 已知四棱锥 , 则中 , 直角三角形最多可以有 (A 1个B2个 C 3个D4个二．填空题（每题 4 分，共16 分）11. 已知ABC的两边 AC,BC分别交平面于点M,N，设直线AB与平面交于点O，则点 O与直线 MN的位置关系为 _________12.过直线外一点与该直线平行的平面有 ___________个，过平面外一点与该平面平行的直线有_____________条13. 一块西瓜切 3 刀最多能切 _________块14.将边长是 a 的正方形 ABCD沿对角线 AC 折起 , 使得折起后 BD得长为 a, 则三棱锥D-ABC的体积为 ___________三、解答题15（10 分）如图，已知 E,F 分别是正方形ABCD A1B1C1 D1的棱 AA1和棱 CC1上的点，且 AE C1 F 。

高一数学立体几何初步试题答案及解析1.以下命题正确的是A．两个平面可以只有一个交点B．一条直线与一个平面最多有一个公共点C．两个平面有一个公共点，它们可能相交D．两个平面有三个公共点，它们一定重合【答案】C【解析】两个平面只要有一个公共点，就有一条通过该点的公共直线，故A错一条直线若在平面内，其上的所有点都在平面内，故B错两个平面有一个公共点，它们可能相交也可能是同一个平面，故C对，选C。

【考点】本题主要考查平面的基本性质及推论。

点评：基础题，分析选项利用“排除法”。

2.如图所示，点S在平面ABC外，SB⊥AC，SB＝AC＝2， E、F分别是SC和AB的中点，则EF的长是（）A．1B．C．D．【答案】B【解析】取BC的中点D，连接ED与FD∵E、F分别是SC和AB的中点，点D为BC的中点∴ED∥SB，FD∥AC而SB⊥AC，SB=AC=2则三角形EDF为等腰直角三角形则ED=FD=1即EF=，故选B。

【考点】本题主要考查点、线、面间的距离计算。

点评：本题主要考查了中位线定理，以及异面直线所成角的应用，同时考查了转化与化归的思想，属于基础题。

3.已知ABCD是空间四边形形，E、F、G、H分别是AB、BC、CD、DA的中点，如果对角线AC＝4，BD＝2，那么EG2＋HF2的值等于A．10 B．15 C．20 D．25【答案】A【解析】因为，所以是平行四边形，，，又因为两式相加得，故选A。

【考点】本题主要考查空间四边形的性质、余弦定理的应用。

点评：利用空间四边形的性质，可以得到若干平行关系，利用余弦定理得出EG2，HF2，两式相加“消去”了未知量。

4.说出下列三视图表示的几何体是A．正六棱柱B．正六棱锥C．正六棱台D．正六边形【答案】A【解析】结合简单几何体的特征，对照选项知A。

【考点】本题主要考查简单几何体的特征及三视图。

点评：简单题，理解好三视图的意义。

5.平行投影与中心投影之间的区别是_____________；【答案】平行投影的投影线互相平行,而中心投影的投影线相交于一点；【解析】平行投影与中心投影之间的区别是平行投影的投影线互相平行,而中心投影的投影线相交于一点。

一．选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的) 1、下列命题为真命题的是（ ）A. 平行于同一平面的两条直线平行；B.与某一平面成等角的两条直线平行；C. 垂直于同一平面的两条直线平行；D.垂直于同一直线的两条直线平行。

2、下列命题中错误的是：（ ）A. 如果α⊥β，那么α内一定存在直线平行于平面β；B. 如果α⊥β，那么α内所有直线都垂直于平面β；C. 如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；D. 如果α⊥γ，β⊥γ，α∩β＝l,那么l ⊥γ.3、右图的正方体ABCD-A ’B ’C ’D ’中,异面直线AA ’与BC 所成的角是（ ） A. 300 B.450 C. 600 D. 900 4、右图的正方体ABCD- A ’B ’C ’D ’中，二面角D ’-AB-D 的大小是（ ）A. 300B.450C. 600D. 900 5.在空间中，下列命题正确的是A.若三条直线两两相交，则这三条直线确定一个平面B.若直线m 与平面α内的一条直线平行，则α//mC.若平面βα⊥，且l =βα ，则过α内一点P 与l 垂直的直线垂直于平面βD.若直线a 与直线b 平行，且直线a l ⊥，则b l ⊥6．设平面α∥平面β，A ，C ∈α，B ，D ∈β，直线AB 与CD 交于点S ，且点S 位于平面α，β之间，AS ＝8，BS ＝6，CS ＝12，则SD ＝（ ）A ．3B ．9C ．18D ．10 7．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )A ．9πB ．10πC ．11πD ．12πA B DA ’B ’D ’ C C ’ABD CE F8. 正方体的内切球和外接球的半径之比为（ ）A. 3:1B. 3:2C. 3:3D. 2:39．已知△ABC 是边长为a 2的正三角形，那么它的斜二侧所画直观图A B C 的面积为( )A.32a 2 B.34a 2 C.64a 2 D.6a 210．若正方体的棱长为2，则以该正方体各个面的中心为顶点的多面体的体积为( )A.26B.23C.33D.2311. 在空间四边形ABCD 中，AD=BC=2，E 、F 分别是AB 、CD 的中点，EF=2，求AD 与BC 所成角的大小．( )A. 30B. 45C.60οD. 90 12.如图，在多面体ABCDEF 中，已知平面ABCD 是边长为3的正方形，//EF AB ,32EF =,且EF 与平面ABCD 的距离为2，则该多面体的体积为（ ） A92B 5C 6D 152二、填空题（共4小题，每小题5分，共20分，把答案填在题中的横线上）13． Rt ABC ∆中，3,4,5AB BC AC ===，将三角形绕直角边AB 旋转一周所成的几何体的体积为.14．一个圆台的母线长为5 cm ，两底面面积分别为4πcm 2 和25π cm 2.则圆台的体积 ________． 15. 三棱锥S-ABC 中SA平面ABC ，AB 丄BC,SA= 2,AB =B C=1，则三棱锥S-ABC 的外接球的表面积等于______.16．如图，在直角梯形ABCD 中，,,BC DC AE DC ⊥⊥M 、N 分别是AD 、BE 的中点，将三角形ADE 沿AE 折起。

高一数学立体几何试题答案及解析1.设三棱柱的体积为，分别是侧棱上的点，且，则四棱锥的体积为（）A．B．C．D．【答案】C【解析】假设重合，重合,则【考点】棱柱棱锥的体积2.如图，四棱锥中，，四边形是边长为的正方形，若分别是线段的中点．（1）求证：∥底面；（2）若点为线段的中点，求三角形的面积。

【答案】（1）见解析；（2）【解析】要想证明线面平行，只需证明出该线段与面内的任意一条线段平行即可，在本题中，需要连接辅助线进行解答，在解此问题时主要运用了三角形内中位线平行于底边的性质；首先需要掌握知识，三角形的中位线的长度为底边的一半，先求出所需边的长度，再运用余弦定理，求出角的度数，在运用三角形面积公式即可得到结果。

试题解析：（1）解：连接，由题意知，为中点，为的中位线，平面平面平面（2）连接由（1）知：，同理可得：，，【考点】空间几何的运算3.如图，在四棱台中，底面，四边形为正方形，，，平面．（1）证明：为的中点；（2）求点到平面的距离．【答案】（1）详见解析；（2）【解析】（1）根据线面平行的性质定理，线面平行则，线线平行，所以可证,可证四边形是平行四边形，即证明是中点；（2）根据等体积转化,可证是直角三角形，写出体积公式，求解距离．试题解析：解（1）连接AD1，则D1C1∥DC∥AB，∴A、E、C1、D1四点共面，∵C1E∥平面ADD1A1，则C1E∥AD1，∴AEC1D1为平行四边形，∴AE＝D1C1＝1，∴E为AB的中点．（6分）（2），∵AD⊥DC，AD⊥DD1，∴AD⊥平面DCC1D1，AD⊥DC1．设点E到平面ADC1的距离为h，则，解得．【考点】1．线面平行的性质定理；2．等体积转化．4.设长方体的长、宽、高分别为2，1, 1，其顶点都在同一个球面上，则该球的体积为_______．【答案】【解析】球直径为长方体的体对角线，故半径为【考点】球内接长方体的性质，球体积的计算5.（本小题12分）如图所示，三棱柱ABC－A1B1C1中，．（1）证明：；（2）若，求三棱柱ABC－A1B1C1的体积．【答案】（1）见解析；（2）3【解析】（1）取AB的中点O，连接OC，OA1，A1B，证得，，则根据线面垂直的判定定理可得，进而得出；（2）先证明，进而证出，再求出，最后利用柱体的体积公式求出体积；试题解析：（1）取AB 的中点O ，连接．因为，所以．由于，故△AA 1B 为等边三角形，所以．因为，所以．又，故．（2）由题设知△ABC 与△AA 1B 都是边长为2的等边三角形，所以． 又，则，故．因为所以，为三棱柱的高．又△ABC 的面积，故三棱柱的体积．【考点】1．线面垂直的判定定理；2．线线垂直的证明方法；3．柱体的体积公式；6. 如图，ABCD －A 1B 1C 1D 1为正方体，下面结论错误的是（ ）．A ．BD ∥平面CB 1D 1 B ．AC 1⊥BDC ．AC 1⊥平面CB 1D 1D ．异面直线AD 与CB 1角为60°【答案】D【解析】因为易证∥，由线面平行的判定定理可证得∥面，所以A 选项结论正确； 由正方体可得面，可证得，由为正方体得，因为，所以面，从而可证得．同理可证明，根据线面垂直的判定定理可证得面，所以B ，C 选项结论都正确； 因为∥，所以为异面直线与所成的角，由正方体可得，所以D 选项的内容不正确． 故选D 。

高一立体几何试卷及答案The document was prepared on January 2, 2021立体几何试题一．选择题每题4分,共40分1.已知AB 0300300150空间,下列命题正确的个数为1有两组对边相等的四边形是平行四边形,2四边相等的四边形是菱形3平行于同一条直线的两条直线平行 ;4有两边及其夹角对应相等的两个三角形全等A 1B 2C 3D 43.如果一条直线与两个平行平面中的一个平行,那么这条直线与另一个平面的位置关系是A 平行B 相交C 在平面内D 平行或在平面内4.已知直线m αα过平面α外一点,作与α平行的平面,则这样的平面可作A 1个 或2个B 0个或1个C 1个D 0个6.如图,如果MC ⊥菱形ABCD 所在平面,那么MA 与BD 的位置关系是A 平行B 垂直相交C 异面D 相交但不垂直7.经过平面α外一点和平面α内一点与平面α垂直的平面有A 0个B 1个C 无数个D 1个或无数个8.下列条件中,能判断两个平面平行的是A 一个平面内的一条直线平行于另一个平面;B 一个平面内的两条直线平行于另一个平面C 一个平面内有无数条直线平行于另一个平面D 一个平面内任何一条直线都平行于另一个平面9.对于直线m ,n 和平面,αβ,使αβ⊥成立的一个条件是A //,,m n n m βα⊥⊂B //,,m n n m βα⊥⊥C ,,m n m n αβα⊥=⊂D ,//,//m n m n αβ⊥10 .已知四棱锥,则中,直角三角形最多可以有A 1个B 2个C 3个D 4个二．填空题每题4分,共16分11.已知∆ABC 的两边AC,BC 分别交平面α于点M,N,设直线AB 与平面α交于点O,则点O 与直线MN 的位置关系为_________12.过直线外一点与该直线平行的平面有___________个,过平面外一点与该平面平行的直线有_____________条13.一块西瓜切3刀最多能切_________块14.将边长是a 的正方形ABCD 沿对角线AC 折起,使得折起后BD 得长为a,则三棱锥D-ABC 的体积为___________三、 解答题1510分如图,已知E,F 分别是正方形1111ABCD A B C D -的棱1AA 和棱1CC 上的点,且1AE C F =.求证：四边形1EBFD 是平行四边形1610分如图,P 为ABC ∆所在平面外一点,AP=AC,BP=BC,D 为PC 的中点, 证明：直线PC 与平面ABD 垂直CB1712分如图,正三棱锥A-BCD,底面边长为a,则侧棱长为2a,E,F分别为AC,AD 上的动点,求截面BEF∆周长的最小值和这时E,F的位置.DC1812分如图,长方形的三个面的对角线长分别是a,b,c,求长方体对角线AC'的长C1bC BA答案1三点共线2无数 无数3a 1证明: 1AE C F = 11AB C D =11EAB FC D ∠=∠∴ 11EAB FC D ∆≅∆1EB FD ∴=过1A 作11//A G D F又由1A E ∥BG 且1A E =BG可知1//EB AG 1//EB D F ∴∴四边形1EBFD 是平行四边形2 ∵AP AC =D 为PC 的中点∴AD PC ⊥∵BP BC =D 为PC 的中点∴BD PC ⊥∴PC ⊥平面ABD∴AB PC ⊥3 提示:沿AB 线剪开 ,则BB '为周长最小值.易求得EF 的值为34a ,则周长最小值为114a . 4解:()()()222AC AC CC ''=+ ()()222()AB BC CC '=++222a b c =++。

高一立体几何测试题A ．圆锥B ．四棱锥C ．三棱锥D ．三棱台 2、下列几种说法正确的个数是（ B ） ①三点可以确定一个平面②用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台 ③垂直于同一直线的两个平面互相平行。

④空间中如果两个角的两边分别对应平行，那么这两个角相等。

⑤斜二测画法作直观图时，平行的线段在直观图中对应的线段仍然平行 A ．1 B ．2 C ．3 D ．43、正方体ABCD- A 1B 1C 1D 1中，二面角D 1-AB-D 的大小是（ ） A. 300 B.450 C. 600 D. 9004、已知直线a 、b 与平面α、β、γ，下列条件中能推出α∥β的是（ A ） A ．a ⊥α且a ⊥β B ．α⊥γ且β⊥γ C ．a ⊂α，b ⊂β，a ∥b D ．a ⊂α，b ⊂α，a ∥β，b ∥β5、已知正方体外接球的体积是π332，那么正方体的棱长等于（ D ）A.22B.332 C.324 D.334 解：正方体外接球的体积是323π，则外接球的半径R=2，正方体的对角线的长为4，棱长等于3，选. 6、右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ） A ．9π B ．10πC ．11πD ．12π7、正方体ABCD-A 1B 1C 1D 1中，AB 的中点为M ， DD 1的中点为N ，异面直线俯视图 正视图 侧视图B 1M 与CN 所成的角的余弦值是（ ）A ．21B ．0 C．2D．8、如图，在侧棱和底面垂直的四棱柱ABCD-A 1B 1C 1D 1中，当底面ABCD 满足 ？条件时，有1A C B D。

不正确的条件是（ ）A ．四边形ABCD 是菱形B ．四边形ABCD 是正方形C ．四边形ABCD 是对角线互相垂直的四边形D ．四边形ABCD 是矩形9、某空间几何体的正视图与俯视图如下图，则它的侧视图为（ C ）俯视图正视图AB10、在酒泉卫星发射场某试验区，用四根垂直于地面的立柱支撑着一个平行四边形的太阳能电池板，可测得其中三 根立柱1AA 、1BB 、1CC 的长度分别为m 10、m 15、m 30，则立柱1DD 的长度是（B ） A ．m 30 B ．m 25 C ．m 20 D ． m 1511、已知ABCD 是空间四边形形，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，如果对角线AC ＝4，BD ＝2，那么EG 2＋HF 2的值等于 （ A ） A ．10B ．15C ．20D ．25C12、如图，三角形ABC 中，AB ⊥BC ，30CAB ∠=︒，PA ⊥平面ABC ，DA=AC=2a ，则三棱锥A-BCD 的高为（ ）ABC．7 D．2113．已知m 、l 是直线, αβ、是平面, 给出下列命题: ①若l 垂直于α内的两条相交直线, 则l ⊥α； ②若l 平行于α, 则l 平行α内所有直线； ③若m l l m ⊂⊂⊥⊥αβαβ,,，且则； ④若l l ⊂⊥⊥βααβ,且，则；⑤若,,m l m l αβαβ⊂⊂，且∥则∥；⑥m n αα⊥⊥且，则m ∥n其中正确的命题的序号是①④⑥ (注: 把你认为正确的命题的序号都填上)．14、长方体ABCD —A 1B 1C 1D 1中，AB=2，BC=3，AA 1=5，则一只小虫从A 点沿长方体的表面爬到C 1点的最短距离是 ．14．52．15、半径为4的球O 内有一内接矩形ABCD ，AB=6，BC=则四棱锥O-ABCD 的体积为： 。

高中几何体试题及答案解析试题一：立体几何基础题题目：已知一个长方体的长、宽、高分别为a、b、c，求该长方体的体积。

解析：长方体的体积可以通过其三个维度的乘积来计算，即体积V = a × b × c。

答案：V = abc。

试题二：空间向量在立体几何中的应用题目：在空间直角坐标系中，点A(1, 0, 0)，点B(0, 1, 0)，点C(0, 0, 1)，求三角形ABC的面积。

解析：空间直角坐标系中，三角形的面积可以通过向量叉乘来求解。

设向量AB = (-1, 1, 0)，向量AC = (-1, 0, 1)，向量AB与向量AC 的叉乘结果为向量AB × AC = (1, -1, 1)。

该向量的模即为三角形ABC的面积的两倍。

答案：三角形ABC的面积为√3。

试题三：圆锥体的体积计算题目：已知圆锥的底面半径为r，高为h，求圆锥的体积。

解析：圆锥的体积可以通过公式V = (1/3)πr²h来计算。

答案：V = (1/3)πr²h。

试题四：球体的表面积与体积题目：已知球体的半径为R，求球体的表面积和体积。

解析：球体的表面积可以通过公式A = 4πR²来计算，球体的体积可以通过公式V = (4/3)πR³来计算。

答案：球体的表面积A = 4πR²，球体的体积V = (4/3)πR³。

试题五：旋转体的体积题目：已知圆柱的底面半径为r，高为h，求圆柱的体积。

解析：圆柱的体积可以通过公式V = πr²h来计算。

答案：V = πr²h。

结束语：通过上述试题及答案解析，我们可以看到高中几何体的计算涉及体积、面积和表面积等概念，这些计算在数学和物理等多个领域都有广泛的应用。

掌握这些基础知识对于解决更复杂的几何问题至关重要。

希望这些试题和解析能够帮助学生加深对立体几何概念的理解，并在解题过程中培养空间想象能力。

高一立体几何试题及答案一、选择题（每题4分，共40分）1. 若一个长方体的长、宽、高分别为a、b、c，则该长方体的体积为（）A. abcB. ab+bc+acC. a^2b^2c^2D. a^2+b^2+c^2答案：A2. 一个正方体的棱长为a，则其表面积为（）A. 6a^2B. 8a^2C. 10a^2D. 12a^23. 一个圆柱的底面半径为r，高为h，则其体积为（）A. πr^2hB. 2πr^2hC. πr^3D. 2πr^3答案：A4. 一个圆锥的底面半径为r，高为h，则其体积为（）A. 1/3πr^2hB. 1/2πr^2hC. πr^2hD. 2πr^2h答案：A5. 一个球的半径为r，则其体积为（）B. 2/3πr^3C. 1/3πr^3D. 3/4πr^3答案：A6. 若一个三棱锥的四个顶点分别为A、B、C、D，且AB=AC=AD=BC=BD=CD=a，则该三棱锥为（）A. 正四面体B. 正三棱锥C. 正六棱锥D. 正八棱锥答案：A7. 若一个三棱柱的底面为等边三角形，且侧棱与底面垂直，则该三棱柱为（）B. 斜三棱柱C. 直三棱柱D. 正六棱柱答案：A8. 若一个四棱锥的底面为正方形，且侧棱与底面垂直，则该四棱锥为（）A. 正四棱锥B. 斜四棱锥C. 直四棱锥D. 正八棱锥答案：A9. 若一个五棱锥的底面为正五边形，且侧棱与底面垂直，则该五棱锥为（）B. 斜五棱锥C. 直五棱锥D. 正十棱锥答案：A10. 若一个六棱锥的底面为正六边形，且侧棱与底面垂直，则该六棱锥为（）A. 正六棱锥B. 斜六棱锥C. 直六棱锥D. 正十二棱锥答案：A二、填空题（每题4分，共20分）11. 一个长方体的长、宽、高分别为a、b、c，则该长方体的表面积为______。

答案：2(ab+bc+ac)12. 一个正方体的棱长为a，则其体积为______。

答案：a^313. 一个圆柱的底面半径为r，高为h，则其侧面积为______。

高一数学立体几何练习题及答案一、选择题1. 下列哪个图形不是立体图形？A. 立方体B. 圆锥C. 圆柱D. 正方形答案：D2. 已知一个立方体的边长为5cm，求它的表面积和体积分别是多少？A. 表面积：150cm²，体积：125cm³B. 表面积：100cm²，体积：125cm³C. 表面积：150cm²，体积：100cm³D. 表面积：100cm²，体积：100cm³答案：A3. 以下哪个选项可以形成一个正方体？A. 六个相等的长方体B. 一个正方形和一个长方体C. 六个相等的正方形D. 一个正方形和一个正方体答案：C4. 以下哪个图形可以形成一个圆柱？A. 一个正方形和一个长方体B. 一个圆和一个长方体C. 一个长方形和一个长方体D. 一个正方形和一个正方体答案：C5. 以下哪个选项可以形成一个圆锥？A. 一个圆和一个长方体B. 一个圆和一个正方体C. 一个正方形和一个长方体D. 一个正方形和一个正方体答案：B二、填空题1. 已知一个正方体的表面积为96cm²，求它的边长是多少？答案：4cm2. 已知一个圆柱的半径为3cm，高为10cm，求它的表面积和体积分别是多少？答案：表面积：198cm²，体积：90π cm³3. 以下哪个选项可以形成一个长方体？A. 六个相等的正方形B. 一个圆和一个长方形C. 六个相等的长方形D. 一个正方形和一个正方体答案：C三、解答题1. 某长方体的长、宽、高分别为3cm、4cm、5cm，请回答以下问题：（1）它的表面积是多少？（2）它的体积是多少？答案：（1）表面积 = 2(长×宽 + 长×高 + 宽×高)= 2(3×4 + 3×5 + 4×5)= 2(12 + 15 + 20)= 2(47)= 94cm²（2）体积 = 长×宽×高= 3×4×5= 60cm³2. 某圆锥的半径是5cm，高是12cm，请回答以下问题：（1）它的表面积是多少？（2）它的体积是多少？答案：（1）斜面积= π×半径×斜高= π×5×13≈ 204.2cm²（2）体积= (1/3)π×半径²×高= (1/3)π×5²×12≈ 314.2cm³四、解析题某正方体的表面积是96cm²，它的边长是多少？解答：设正方体的边长为x，由表面积的计算公式可得：表面积 = 6x²96 = 6x²16 = x²x = 4所以，该正方体的边长为4cm。

高一数学立体几何综合试题答案及解析1.等腰梯形，上底，腰，下底，以下底所在直线为x轴，则由斜二测画法画出的直观图的面积为_______．【答案】【解析】如上图，，，，因为，所以，所以，在直观图中，【考点】斜二测画法2.在四边形中，∥，，将沿折起，使平面平面，构成三棱锥，则在三棱锥中，下列命题正确的是（）A．平面平面B．平面平面C．平面平面D．平面平面【答案】D【解析】∵在四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD，且平面ABD∩平面BCD=BD.故CD⊥平面ABD，则CD⊥AB，又AD⊥AB,故AB⊥平面ADC，所以平面ABC⊥平面ADC．故选D．【考点】折叠问题，垂直关系。

点评：中档题，对于折叠问题，要特别注意“变”与“不变”的几何元素，及几何元素之间的关系。

3.已知、是不同的平面，、是不同的直线，则下列命题不正确的（）A．若∥则B．若∥,则∥C．若∥，，则D．若则∥【答案】B【解析】A项中∥；B项中直线，可能平行可能异面；C项依据线面垂直的判定定理可知成立；D项依据垂直于同一直线的两平面平行可知结论正确【考点】空间线面间平行垂直的判定点评：本题用到了判定定理有：一个平面经过另一平面的一条垂线则两面垂直，两条平行直线中的一条垂直于平面则另一条也垂直于平面，垂直于同一直线的两平面平行4.①分别与两条异面直线都相交的两条直线一定是异面直线；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中为真命题的是（）A．①和②B．②和④C．③和④D．②和③【答案】B【解析】解：因为①分别与两条异面直线都相交的两条直线一定是异面直线；可能平行，因此错误。

②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；成立③垂直于同一直线的两条直线相互平行；可能相交，错误④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．成立故选B5.如图，正四棱锥中，侧棱与底面所成角的正切值为．（1）求侧面与底面所成二面角的大小；（2）若E是PB中点，求异面直线PD与AE所成角的正切值．【答案】（1）连结AC，BD交于点O，连结PO，则PO⊥面ABCD，∴∠PAO就是PA与底面ABCD所成的角，∴ tan∠PAO=．设AB=1，则PO=AOtan∠PAO =．设F为AD中点，连FO、PF，易知OF⊥AD，PF⊥AD，所以∠PAO就是侧面PAD与底面ABCD所成二面角的平面角．在Rt中，，∴，即侧面PAD与底面ABCD所成二面角的大小为；（2）连结EO，由于O为BD中点，E为PD中点，所以．∴就是异面直线PD与AE所成的角．在Rt中，．∴．由，可知面．所以，在Rt中，，即异面直线PD与AE所成角的正切值为．【解析】略6.（本小题满分16分）如图，多面体中,两两垂直，平面平面，平面平面，.(1)证明四边形是正方形；(2)判断点是否四点共面，并说明为什么？(3)连结，求证：平面.【答案】证明：（1）…………..2分同理，……..3分则四边形是平行四边形.又四边形是正方形. ……..4分(2) 取中点，连接.在梯形中，且.又且,且.……………………..5分四边形为平行四边形, ……………………..6分. ……………………..7分在梯形中,, ……………………..9分四点共面. …………………….10分（3）同（1）中证明方法知四边形BFGC为平行四边形.且有，从而,. ……………………..12分又故，而,故四边形BFGC为菱形， . ……………………..14分又由知.正方形中，，故.. ……………………..16分【解析】略7.（本小题満分12分）如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点．（Ⅰ）证明AD⊥D1F;（Ⅱ）求AE与D1F所成的角;（Ⅲ）证明面AED⊥面A1FD1;【答案】（Ⅰ）∴AD⊥D1F（Ⅱ）∴AE⊥D1FAE与D1F所成的角为900（Ⅲ）由以上可知D1F⊥平面AED∴面AED⊥面A1FD1;【解析】略8.（本小题满分12分）如图，在三棱柱中，面，，，分别为，的中点．（1）求证：∥平面；（2）求证：平面；（3）直线与平面所成的角的正弦值．【答案】（1）证明：连结，与交于点，连结．因为，分别为和的中点，所以∥．又平面，平面，所以∥平面．（2）证明：在直三棱柱中，平面，又平面，所以．因为，为中点，所以．又，所以平面．又平面，所以．因为四边形为正方形，，分别为，的中点，所以△≌△，．所以．所以．又，所以平面．（3）设CE与C1D交于点M，连AM由（2）知点C在面AC1D上的射影为M，故∠CAM为直线AC与面AC1D所成的角，又A1C1//AC所以∠CAM亦为直线A1C1与面AC1D所成的角。

高一数学立体几何综合试题1.如图是一个正方体的展开图，如果将它还原为正方体，那么AB，CD，EF，GH这四条线段所在的直线是异面直线的有（）A．1对B．2对C．3对D．4对【答案】C【解析】如图所示：把展开图再还原成正方体，由经过平面外一点和平面内一点的直线和平面内不进过该点的直线是异面直线可得，AB，CD，EF，GH这四条线段所在直线是异面直线的有：AB和 CD，AB 和 HG，EF 和 HC，共三对，故选 C．【考点】展开图还原几何体，异面直线.2.如图，三棱柱的三视图，主视图和侧视图是全等的矩形，俯视图是等腰直角三角形，点M是A1B1的中点。

（I）求证：B1C//平面AC1M；（II）求证：平面AC1M⊥平面AA1B1B．【答案】（1）证明见解析；（2）证明见解析.【解析】（1）由三视图还原为空间几何体的实际形状时，要从三视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线.在还原空间几何体的实际形状时，一般以正视图和俯视图为主，结合侧视图进行综合考虑；（2）证明线面平行常用方法：一是利用线面平行的判定定理，二是利用面面平行的性质定理，三是利用面面平行的性质；（3）证明两个平面垂直，首先考虑直线与平面垂直，也可以简单记为“证面面垂直，找线面垂直”，是化归思想的体现，这种思想方法与空间中的平行关系的证明类似，掌握化归与转化思想方法是解决这类题的关键.试题解析：证明：（I）由三视图可知三棱柱为直三棱柱，底面是等腰直角三角形且，连结A1C，设。

连结MO，由题意可知A1O=CO，A1M=B1M，所以 MO//B1C．又平面;平面，所以平面 6分（II），又为的中点，平面，平面又平面所以平面AC1M⊥平面AA1B1B 12分【考点】(1)直线与平面平行的判定；（2）平面与平面垂直的判定.3.如图所示，直观图四边形是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( )A．B．C．D．【答案】A【解析】由题可得A¢D¢=A¢B¢=1,B¢C¢=1+,所以原平面图形中AD=1，AB=2，BC=1+,根据梯形的面积计算公式可得【考点】斜二测画法.4.在空间直角坐标系中，以点为顶点的是以为底边的等腰三角形，则实数x的值为（）A．-2B．2C．6D．2或6【答案】D【解析】因为在空间直角坐标系中，以点为顶点的是以为底边的等腰三角形.所以可得.有空间两点间的距离公式可得，解得.故选D.【考点】1.空间中的两点的距离公式.2.解二次方程的能力.5.如图，空间四边形的对棱、成的角，且，平行于与的截面分别交、、、于、、、．（１）求证：四边形为平行四边形；（２）在的何处时截面的面积最大？最大面积是多少？【答案】（１）利用线面平行的性质得到线线平行，然后再利用平行四边形的定义即可证明．（２）当E为AB的中点时，截面面积最大，，【解析】（１）平面，平面，平面平面，．同理，，同理，四边形为平行四边形．（２）与成角，或，当E为AB的中点时，截面面积最大，，【考点】本题考查了线面平行的性质及平行四边形的概念、面积点评：证明两直线平行的方法有：①依定义采用反证法；②利用公理4；③线面平行的性质定理；④面面平行的性质定理6.如图：是⊙的直径，垂直于⊙所在的平面，PA="AC," 是圆周上不同于的任意一点，(1) 求证：平面。

高一数学立体几何综合试题答案及解析1.在空间直角坐标系中，以点为顶点的是以为底边的等腰三角形，则实数x的值为（）A．-2B．2C．6D．2或6【答案】D【解析】因为在空间直角坐标系中，以点为顶点的是以为底边的等腰三角形.所以可得.有空间两点间的距离公式可得，解得.故选D.【考点】1.空间中的两点的距离公式.2.解二次方程的能力.2.如图：是⊙的直径，垂直于⊙所在的平面，PA="AC," 是圆周上不同于的任意一点，(1) 求证：平面。

(2) 求二面角 P-BC-A 的大小。

【答案】（1）利用线面垂直的性质可得线线垂直，再利用线面垂直的判定定理，可得结论；（2）∠PCA=450【解析】试题分析（1）利用线面垂直的性质可得线线垂直，再利用线面垂直的判定定理，可得结论；（2）利用二面角的求解。

因为因为PA⊥平面ABC，且BC⊂平面ABC，所以PA⊥BC．又△ABC中，AB是圆O的直径，所以BC⊥AC．、又PA∩AC=A，所以BC⊥平面PAC．（2）在第一问的基础上，由于是⊙的直径，垂直于⊙所在的平面，PA="AC," 是圆周上不同于的任意一点，那么可知二面角 P-BC-A 的大小450【考点】空间图形的位置关系点评：本题考查直线与平面垂直的判定定理，平面与平面垂直的判定定理，考查空间图形的位置关系，属于中档题．3.已知正方体中，面中心为．（1）求证：面；（2）求异面直线与所成角．【答案】（1）对于线面平行的证明一般要利用其判定定理来求证。

（2）【解析】（1）证明：连结，设，连结，则四边形为平行四边形，∴又∵，∴面． 6分（2）解：由（1）可知，为异面直线与所成角（或其补角），设正方体的边长2，则在中，，，，∴为直角三角形，∴． 6分【考点】异面直线的角，线面平行点评：解决的关键是熟练的根据几何中的性质定理和判定定理来求解，属于基础题。

4.、经过空间一点作与直线成角的直线共有（）条A．0B．1C．2D．无数【答案】D【解析】若点P在直线l上，可以做无数条直线与直线l成角,这些线成一个圆锥形状.若点P不在直线l上，可以过点P作一条直线与l平行，然后以为一个圆锥的高，P为圆锥的顶点，其中母线与轴角，所以能做无数条.5.已知a、b是两条异面直线，c∥a，那么c与b的位置关系（）A．一定是异面B．一定是相交C．不可能相交D．不可能平行【答案】D【解析】解：6.已知两直线m、n，两平面α、β，且．下面有四个命题( )(1)若； (2)；(3； (4)．其中正确命题的个数是A．０B．１C．2D．3【答案】C【解析】，所以，则存在有。

高一数学立体几何初步试题答案及解析试题一：求证：直线AB与平面P垂直。

已知：直线AB在平面P内，点C在平面P外，且BC垂直于平面P。

求证：直线AB与平面P垂直。

答案：证明：过点C作CD垂直于平面P，交平面P于点D。

因为BC垂直于平面P，所以CD与BC平行。

由平行线性质，∠BCD为直角，因此∠ACD也为直角。

因为AB在平面P内，所以∠ADB为直角。

由于∠ACD和∠ADB都是直角，所以直线AB与平面P垂直。

解析：本题主要考查直线与平面的位置关系。

通过过点C作垂线CD，利用平行线性质和直角三角形的性质，证明了直线AB与平面P垂直。

试题二：已知正方体ABCD-A1B1C1D1的棱长为a，求点B1到平面ABCD的距离。

答案：解：点B1到平面ABCD的距离即为线段B1B的长度。

因为B1B是正方体的高，所以B1B = a。

所以，点B1到平面ABCD的距离为a。

解析：本题考查了正方体的性质。

正方体的高即为从一个顶点到与之相对的面的距离，因此直接利用正方体的性质得到答案。

试题三：已知平面ABC与平面P相交于直线L，点D在直线L上，且AD垂直于平面P，BD = CD，求证：平面BCD垂直于平面P。

答案：证明：因为AD垂直于平面P，所以AD垂直于直线L。

因为BD = CD，所以三角形BCD是等腰三角形，且BC垂直于CD。

因此，平面BCD包含直线CD，且CD垂直于平面P。

由平面垂直的判定定理，平面BCD垂直于平面P。

解析：本题考查了平面与平面垂直的判定定理。

通过证明直线CD垂直于平面P，利用等腰三角形的性质和垂直的判定定理，证明了平面BCD垂直于平面P。

试题四：已知圆柱的底面半径为r，高为h，求圆柱的表面积。

答案：解：圆柱的表面积由底面积和侧面积组成。

底面积S1 = πr^2。

侧面积S2 = 2πrh。

所以，圆柱的表面积S = 2S1 + S2 = 2πr^2 + 2πrh。

解析：本题考查了圆柱的表面积计算。

圆柱的表面积由两个底面和一个侧面组成，通过计算底面积和侧面积，并加总得到圆柱的总表面积。

高一数学立体几何初步试题答案及解析1.点B是点A（1，2，3）在坐标平面内的射影，则OB等于（）A．B．C．D．【答案】B【解析】点A（1，2，3）在坐标平面内的射影为B（0,2,3），所以|OB|=，故选B。

【考点】本题主要考查空间直角坐标系的概念及两点间距离公式的应用。

点评：理解好射影的概念，用熟两点间距离公式。

2.两等角的一组对应边平行，则（）A．另一组对应边平行B．另一组对应边不平行C．另一组对应边也不可能垂直D．以上都不对【答案】D【解析】两等角的一组对应边平行，另一组对应边由多种情况，如平行、相交、异面等，关系D。

【考点】本题主要考查直线的位置关系。

点评：视野要开阔，考虑多种可能情况。

3.经过平面外两点与这个平面平行的平面（）A．只有一个B．至少有一个C．可能没有D．有无数个【答案】C【解析】经过平面外两点与这个平面平行的平面可能没有，如两点所在直线与平面相交时，关系C。

【考点】本题主要考查点线面的关系—--平行关系。

点评：考虑点与平面的多种可能情况思考，结合实物模型探究。

4.如图所示，平面M、N互相垂直，棱l上有两点A、B，AC M，BD N，且AC⊥l，AB＝8cm，AC＝6 cm，BD＝24 cm，则CD＝_________．【答案】26 cm；【解析】连接AD，∵平面M、N互相垂直，AC⊥l，∴AC⊥平面N∴AC⊥CD；∵AB=8cm，AC=6cm，∴BC=10cm，又∵BD=24cm，∴CD=26cm。

【考点】本题主要考查点、线、面间的距离计算、面面垂直。

点评：考查的知识点是空间点到点之间的距离，其中根据面面垂直及线面垂直的性质得到△ABC，△ACD均为直角三角形，是解答本题的关键。

5.下面的图形可以构成正方体的是（）【答案】C【解析】从选项出发，还原成正方体的只有C。

【考点】本题主要考查正方体的展开图。

点评：从选项出发，看能否还原成正方体。

6.下列命题中正确的是（）A．由五个平面围成的多面体只能是四棱锥B．棱锥的高线可能在几何体之外C．仅有一组对面平行的六面体是棱台D．有一个面是多边形，其余各面是三角形的几何体是棱锥【答案】B【解析】由五个平面围成的多面体除四棱锥外，还可以是三棱台；棱锥的高线应是其顶点向底面所作垂线段，斜棱锥的高即在几何体外，故选B。

高一立体几何初步测试题及答案1.在空间四点中，无三点共线是四点共面的（充分不必要条件）。

2.若a∥b，b∩c=A，则a,c的位置关系是（相交直线或异面直线）。

3.圆锥的侧面展开图是直径为a的半圆面，那么此圆锥的轴截面是（等腰直角三角形）。

4.已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为4的等腰三角形，左视图是一个底边长为6、高为4的等腰三角形，则该几何体的体积为（64）。

5.长方体的一个顶点上三条棱长分别是3,4,5，且它的8个顶点都在同一球面上，则这个球的表面积是（50π）。

6.已知正方体外接球的体积是π，那么正方体的棱长等于（3）。

7.若l、m、n是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是（若α⊥β,l∈α,n∈β，则l⊥n）。

8.如图，在正方体ABCD-A' B' C' D'中，E，F，G，H分别为AA'，AB，BB'，B'C'的中点，则异面直线EF与GH所成的角等于（90°）。

9.已知两个平面垂直，其中正确的命题数量是（2）。

10.平面α与平面β平行的条件可以是（直线a//α,a//β）。

三、简答题（本大题共4小题，每小题10分，共40分）1.如何确定一个圆锥的侧面展开图？答：将圆锥展开，使其侧面展开为一段扇形，然后将扇形展开成一个直角三角形，即可得到圆锥的侧面展开图。

2.如何确定一个几何体的三视图？答：俯视图是从正上方看几何体，可以看到几何体的顶面和底面；正视图是从正前方看几何体，可以看到几何体的前面和后面；左视图是从正左方看几何体，可以看到几何体的左面和右面。

通过这三个视图，可以确定一个几何体的形状和尺寸。

3.如何判断两个平面是否平行？答：如果两个平面的法向量平行，则这两个平面平行。

也可以通过判断它们的交线是否平行来确定两个平面是否平行。

4.如何判断两条直线是否相交？答：如果两条直线的方向向量不平行，则它们相交；如果两条直线的方向向量平行但不重合，则它们异面直线；如果两条直线的方向向量重合，则它们可能重合也可能平行。

高一数学立体几何试题答案及解析1.如图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为（）A．B．C．D．【答案】A【解析】略2.在正方体ABCD–A1B1C1D1中，已知E是棱C1D1的中点，则异面直线B1D1与CE所成角的余弦值的大小是（）A．B．C．D．【答案】Ｄ【解析】略3.如图1，正方体中，、是的三等分点，、是的三等分点，、分别是、的中点，则四棱锥的侧视图为（）【答案】C【解析】侧视图从左向右投影，对应，对应，对应，对应，因此侧视图为C项【考点】三视图4.已知直线，平面，下列命题正确的是（）A．B．C．D．【答案】D【解析】根据两个平面平行的判定定理:一个平面内的两条相交直线和另一个平面平行，则这两个平面平行，符号表示为：；【考点】空间中两个平面平行的判定定理；5.（本小题满分13分）如图，在棱长均为的直三棱柱中，是的中点．（1）求证：平面；（2）求直线与面所成角的正弦值．【答案】（1）见解析；（2）．【解析】（1）直三棱柱的侧棱和底面垂直，从而可得到AD⊥BB1，并且AD⊥BC，从而由线面垂直的判定定理可得到AD⊥平面BCC1B1；（2）连接C1D，从而可得到∠AC1D为直线AC1和平面BCC1B1所成角，在Rt△AC1D中，容易求出AD，AC1，从而sin∠AC1D=．试题解析：（1）直三棱柱中，，又，D是BC的中点，，平面；（2）连接，由（1）平面，则即为直线与面所成角，在直角中，，，，．即直线与面所成角的正弦值为．【考点】直线与平面所成的角；直线与平面垂直的判定．6.正方体的表面积为24，则该正方体的内切球的体积为____________．【答案】【解析】正方形边长设为，内切球的直径为2，所以体积为【考点】正方体与球的基本知识7.在正方体ABCD－A1B1C1D1中，二面角C1－AB－C的平面角等于（）A．30°B．45°C．60°D．90°【答案】B【解析】根据二面角的定义，是所求二面角的平面角，易得：．【考点】二面角8.已知是直线，是平面，下列命题中：①若垂直于内两条直线，则；②若平行于，则内可有无数条直线与平行；③若m⊥n，n⊥l则m∥l；④若，则；正确的命题个数为（）A．1B．2C．3D．4【答案】A【解析】①改为垂直于平面内的两条相交直线；②正确；③改为或相交或异面；④改为或异面．故选A．【考点】线与线，面与面，线与面位置关系9.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图，则这个平面图形的面积是________【答案】【解析】直观图中等腰直角三角形斜边长为2，所以两条直角边为，面积为1，因为直观图和平面图面积比为，所以平面图形的面积为【考点】平面直观图10.如图，是一个平面图形的水平放置的斜二测直观图，则这个平面图形的面积等于．【答案】【解析】水平放置的斜二测直观图还原成平面图形如上图，由斜二测画法的定义：平行于轴的线段仍平行于轴，长度不变，平行于轴的线段仍平行于轴，但长度减半，所以，，，所以．【考点】斜二测画法.11.如图，是正方体的棱的中点，给出下列命题①过点有且只有一条直线与直线，都相交；②过点有且只有一条直线与直线，都垂直；③过点有且只有一个平面与直线，都相交；④过点有且只有一个平面与直线，都平行．其中真命题是：A．①②③B．①②④C．①③④D．②③④【答案】B【解析】直线与是两条互相垂直的异面直线，点不在这两异面直线中的任何一条上，如图所示：取的中点，则，且，设与交于，则点共面，直线必与直线相交于某点．所以，过点有且只有一条直线与直线都相交；故①正确；过点有且只有一条直线与直线都垂直，此垂线就是棱，故②正确；过点有无数个平面与直线都相交，故③不正确；过点有且只有一个平面与直线都平行，此平面就是过点与正方体的上下底都平行的平面，故④正确．综上，①②④正确，③不正确，故选B．【考点】1．直线与平面平行的性质；2．平面与平面垂直的性质．【思路点睛】本题考查立体几何图形中直线和平面的相交、平行、垂直的性质，体现了数形结合的数学思想，①需要构造一个过点M且与直线AB、B1C1都相交的平面，就可判断；②利用过空间一点有且只有一条直线与已知平面平行判断；③可举反例，即找到两个或两个以上过点m且与直线AB、B1C1都相交的平面，即可判断．④利用线面平行的性质来判断即可．12.若圆锥的表面积是15π，侧面展开图的圆心角是60°，求圆锥的体积________________．【答案】【解析】因为设圆锥的底面半径为，母线为，利用圆锥的底面周长就是圆锥的侧面展开图的弧长，推出底面半径与母线的关系，通过圆锥的表面积求出底面半径，，得，圆锥的高，即圆锥的高为，即圆锥的体积．【考点】锥体的侧面积公式．【思路点睛】设圆锥的底面半径为，母线为，利用圆锥的底面周长就是圆锥的侧面展开图的弧长，推出底面半径与母线的关系，通过圆锥的表面积求出底面半径，求出圆锥的高，然后再根据圆锥的体积公式，即可求出圆锥的体积．13.正六棱柱的底面边长为，侧棱长为1，则动点从沿表面移到点时的最短的路程是．【答案】【解析】如下图所示，作出正六棱柱的展开图，如果动点从经侧面通过移到点时，则路程为；如果动点从经经沿上底面移到点时，根据题目条件，，则路程为；而，所以最短的路程是.【考点】1、棱锥的展开图；2、最值问题．14.若底面为正三角形的几何体的三视图如图所示，则几何体的侧面积为（）A．B．C．D．【答案】D【解析】由三视图可知该几何体为底面为正三角形的直三棱柱，底面三角形的高为，棱柱高为4，设底面边长为x，则解得，故几何体的侧面积为故选：D．【考点】三视图，几何体的侧面积15.如下图所示，观察四个几何体，其中判断正确的是（）A．①是棱台B．②是圆台C．③不是棱锥D．④是棱柱【答案】D【解析】图①不是由棱锥截来的，所以①不是棱台；图②上、下两个面不平行，所以②不是圆台；图④前、后两个面平行，其他面是平行四边形，且每相邻两个四边形的公共边平行，所以④是棱柱；很明显③是棱锥，选D．【考点】空间几何体的结构特征．16.在空间直角坐标系中，给定点，若点与点关于平面对称，点与点关于轴对称，则（）A．2B．4C．D．【答案】A【解析】由题意知：，，则，故选A．【考点】空间两点间的距离公式．17.某几何体的三视图如图所示（单位：），则该几何体的体积是（）A．B．C．D．【答案】C【解析】由三视图可知该几何体的形状是棱长为的正方体上有一个高为的正四棱锥，其体积为．【考点】1、三视图；2、空间几何体的体积．18.（2015秋•大连校级期末）如图，三棱锥P﹣ABC中，平面PAC⊥平面ABC，∠ABC=，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF∥面PBC．（1）证明：EF∥BC．（2）证明：AB⊥平面PFE．（3）若四棱锥P﹣DFBC的体积为7，求线段BC的长．【答案】（1）、（2）见解析；（3）BC=3或BC=．【解析】（1）由EF∥面PBC可得出EF∥BC；（2）由PC=PD=CD=4可知△PDC是等边三角形，故PE⊥AC，由平面PAC⊥平面ABC可得PE⊥平面ABC，故PE⊥AB，由EF∥BC，BC⊥AB可得AB⊥EF，从而AB⊥平面PEF；（3）设BC=x，用x表示出四边形DFBC的面积，根据体积列出方程解出x．解：（1）证明：∵EF∥面PBC．EF⊂面ABC，面PBC∩面ABC=BC，∴EF∥BC．（2）∵由CD=DE+EC=4，PD=PC=4，∴△PDC是等边三角形，∴PE⊥AC，又∵平面PAC⊥平面ABC，平面PAC∩面ABC=AC，PE⊂平面PAC，∴PE⊥平面ABC，∵AB⊂平面ABC，∴PE⊥AB，∵∠ABC=，EF∥BC．∴AB⊥EF，又∵PE⊂平面PEF，EF⊂平面PEF，PE∩EF=E，∴AB⊥平面PEF．（3）设BC=x，则AB=，∴=，∵EF∥BC，∴△AFE∽△ABC，∴．∵AD=AE，，∴S=，四边形DFBC由（2）可知PE⊥平面ABC，且PE=，∴V=，解得x=3或者，∴BC=3或BC=．【考点】直线与平面垂直的判定；棱柱、棱锥、棱台的体积．19.（2015秋•鞍山校级期末）如图，四面体ABCD中，O是BD的中点，△ABD和△BCD均为等边三角形，AB=2，AC=．（Ⅰ）求证：AO⊥平面BCD；（Ⅱ）求O点到平面ACD的距离．【答案】（Ⅰ）见解析；（Ⅱ）．【解析】（1）连结OC，推导出AO⊥BD，AO⊥OC，由此能证明AO⊥平面BCD．（Ⅱ）设点O到平面ACD的距离为h，由V﹣ACD=V A﹣OCD，能求出点O到平面ACD的距离．O证明：（1）连结OC，∵△ABD为等边三角形，O为BD的中点，∴AO⊥BD．∵△ABD和△CBD为等边三角形，O为BD的中点，，∴．在△AOC中，∵AO2+CO2=AC2，∴∠AOC=90°，即AO⊥OC．∵BD∩OC=0，∴AO⊥平面BCD．解：（Ⅱ）设点O到平面ACD的距离为h．∵V﹣ACD=V A﹣OCD，∴．O在△ACD中，AD=CD=2，．而，，∴．∴点O到平面ACD的距离为．【考点】点、线、面间的距离计算；直线与平面垂直的判定．20.平面截球的球面所得圆的半径为1，球心到平面的距离为，则此球的体积为（）A．B．C．D．【答案】B【解析】利用截面圆的性质先求得球的半径长．如图，设截面圆的圆心为，为∴，即球的半径为，∴，故选B.【考点】1、球体的体积；2、球体的性质.【思路点晴】本题考察的是球体的性质，属于中档题目；用平面截球面，得到一个圆，球心到圆心的连线垂直于圆所在的平面，从而得到直角三角形，利用勾股定理即可求出球的半径，再将球的半径代入球的体积公式中，即可求出球的体积．21.某几何体的三视图如图所示，则该几何体的体积为________．【答案】24【解析】由俯视图可以判断该几何体的底面为直角三角形，由正视图和左视图可以判断该几何体是由直三棱柱（侧棱与底面垂直的棱柱）截取得到的．在长方体中分析还原，如图（1）所示，故该几何体的直观图如图（2）所示．在图（1）中，，．故几何体的体积为．【考点】1、三视图；2、组合体的体积.【技巧点晴】本题考查的是空间几何体的体积的求法、三视图问题，属于中档题目；要先从三视图的俯视图入手，如果俯视图是圆，几何体为圆锥或三圆柱，如果俯视图是三角形，几何体为三棱柱或三棱锥；根据三视图得出该几何体为三棱柱截去三棱锥后的几何体，用两个体积相减即可.22.如图所示，在四边形ABCD中，AB=AD=CD=1，BD=，BD CD，将四边形ABCD沿对角线BD折成四面体，使平面平面BCD，则下列结论正确的是 .（1）；（2）；（3）与平面所成的角为；（4）四面体的体积为.【答案】（2）（4）【解析】由BD CD，使平面平面BCD，知平面，所以，又由，得，即，所以平面，即．因此是错误的，是正确的，由上面证明知是与平面所成的角，由知，．故选（2）（4）正确．【考点】命题的真假判断．【名师】折叠问题是考查学生空间想象能力的较好载体．如本题，不仅要求学生象解常规立几综合题一样懂得线线，线面和面面位置关系的判定方法及相互转化，角的作法，还要正确识别出平面图象折叠后的空间图形，更要识得折前折后有关线线、线面位置的变化情况以及有关量（边长与角）的变化情况，否则无法正确解题．这正是折叠问题的价值所在．23.如图，矩形ABCD中，BC=2，AB=1，PA⊥平面ABCD，BE∥PA，BE=PA，F为PA的中点.（1）求证：PC∥平面BDF.（2）记四棱锥C-PABE的体积为V1，三棱锥P-ACD的体积为V2，求的值.【答案】（1）证明见解析；（2）．【解析】（1）要证线面平行，就是要证线线平行，这条平行线就是过的平面与平面的交线，从图中看，设与的交点为，就是要找的平行线，由中位线定理可证得平行；（2）题中四棱锥与三棱锥的体积没有直接的关系，我们可以通过体积公式进行转化，首先，而三棱锥与四棱锥的高相等（同），因此只要求得其底面积之比即可．试题解析：（1）证：连接EF，连接BD交AC与点O，连OF，依题得O为AC中点，又F为PA的中点，所以OF为中位线，所以OF//PC因为所以PC∥平面BDF。