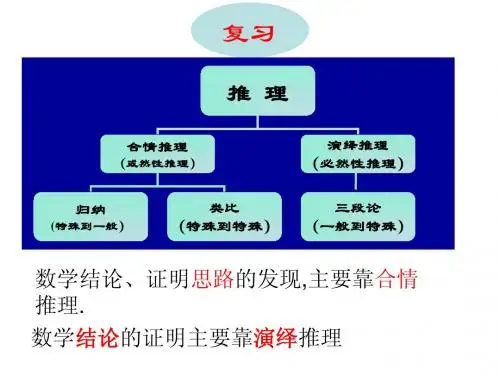
2. 2 .1 综合法和分析法

2.2.1综合法和分析法
1
1.综合法:(顺推证法)(由因导果法)
例:已知a, b 0, 求证:a(b2 c 2 ) b(c 2 a 2 ) 4abc
知识点提示： 基本不等式：a b 2 ab (a 0, b 0) a 2 b 2 2ab
1.综合法:(顺推证法)(由因导果法)
因为log19360<log19361=2， 所以
1 2 3 2 log 5 19 log 3 19 log 2 19
思考题：
已知a, b是正数, 且a b 1, 1 1 求证： 4. a b
当堂训练： 课本P42，练习T1.
课后作业： 课本P44，A组，T1。
例:已知a, b 0, 求证:a(b2 c 2 ) b(c 2 a 2 ) 4abc
2 证明 : : bb 2 c 222bcaa 0 c2 bc, , 0 证明 2 2 证明 : b c 2bc, a 0 aabb 2 c ) ) 22abc. ( ( 2 c 2 2 abc. 2 a (b 2 c 2 ) 2abc. 同理, bbcc 2 a ) ) 22abc. ( ( 2 a 2 2 abc. 同理, 同理, b(c a 2 ) 2abc. aabb 2 c ) ) bcc 2 a ) ) 44abc. ( ( 2 c 2 2 b( ( 2 a 2 2 abc. 2 a (b c 2 ) b(c 2 a 2 ) 4abc.
P Q1
Q1 Q2
Q 2 Q3
Qn Q
综合法是由一个个推理组成的
例1:如图,△ABC在平面α外, AB P, BC Q, AC R. 求证:P,Q,R三点共线.

2
充分条件
思考6：上述证明方法叫做分析法. 一般 地，分析法的基本含义是什么？ 从所证结论出发，逐步寻求使它成立的 充分条件，直到归结为判定一个显然成 立的条件（已知条件、定义、公理、定 理、性质、法则等）为止.
分析法又叫“逆推证法”或“执果索因法”, 其基本思想是：由未知探需知，逐步推向 已知.
2
2
2
2
4abc
其左右两边的结构有什么特点？ 右边是3个数a，b，c的乘积的4倍，左边 为两项之和，其中每一项都是一个数与 另两个数的平方和之积.
思考2：利用哪个知识点可以沟通两个数 的平方和与这两个数的积的不等关系？
基本不等式 x + y
2 2
2xy
思考3：若已知a＞0，b＞0，如何利用不 等式性质证明
证明过程中我们要善于观察变形，合理利用已 知条件、定理、公式，把文字语言转化为符号 语言或者图形语言，由因导果！
探究（二）：分析法
回顾基本不等式： a + b 2 (a>0,b>0)的证明.
ab 证明 : 要证 2 ab ,
ab
只需证
a b 2 ab
只需证
只需证
a+b-2 ab 0
例1.已知 a, b, c 是不全相等的正数 bc a c a b a b c 求证： 3 a b c
(综合法)
R ∵a，b，c ，
符号语言
b a c a c b 与 ， 与 ， 与 均为正实数且不能同时相等， a b a c b c b a c a c b 2， ＋ 2 ， ＋ 2 ， 由重要不等式得： ＋ a b a c b c
2.2直接证明与间接证明
2.2.1 综合法和分析法(1)

§2.2.1 综合法和分析法（3）学习目标1. 能结合已经学过的数学示例,了解综合法和分析法的思考过程和特点;2. 学会用综合法和分析法证明实际问题,并理解分析法和综合法之间的内在联系;3. 养成勤于观察、认真思考的数学品质. 学习过程一、课前准备5051 复习1：综合法是由 导 ; 复习2：分析法是由 索 .二、新课导学 ※ 学习探究探究任务一：综合法和分析法的综合运用 问题：已知,()2k k Z παβπ≠+∈,且2sin cos 2sin ,sin cos sin ,θθαθθβ+=∙=求证:22221tan 1tan 1tan 2(1tan )αβαβ--=++.新知：用P 表示已知条件、定义、定理、公理等，用Q 表示要证明的结论，则上述过程可用框图表示为：试试：已知tan sin ,tan sin a b αααα+=-=，求证：222()16a b ab -=.反思：在解决一些复杂、技巧性强的题目时，我们可以把综合法和分析法结合使用.※ 典型例题例1 已知,A B 都是锐角，且2A B π+≠，(1tan )(1tan )2A B ++=，求证：45A B +=︒变式：已知1tan 12tan αα-=+，求证：3sin 24cos 2αα=-.小结：牢固掌握基础知识是灵活应用两种方法证明问题的前提，本例中，三角公式发挥着重要作用.例2 在四面体P ABC -中，PD ABC ⊥∆，AC BC =，D 是AB 的中点，求证：AB PC ⊥.变式：如果,0a b >，则lg lg lg 22a b a b++≥.小结：本题可以单独使用综合法或分析法进行证明. ※ 动手试试练 1. 设实数,,a b c 成等比数列，非零实数,x y 分别为a 与b ，b 与c 的等差中项，求证2a c x y +=.练2. 已知54A B π+=，且,()2A B k k Z ππ≠+∈，求证：(1tan )(1tan )2A B ++=.三、总结提升 ※ 学习小结1. 直接证明包括综合法和分析法.2. 比较好的证法是：用分析法去思考，寻找证题途径，用综合法进行书写；或者联合使用分析法与综合法，即从“欲知”想“需知”(分析)，从“已知”推“可知”（综合），双管齐下，两面夹击，逐步缩小条件与结论之间的距离，找到沟通已知条件和结论的途径.※ 知识拓展综合法是“由因导果”，而分析法是“执果索因”，它们是截然相反的两种证明方法，分析法便于我们去寻找思路，而综合法便于过程的叙述，两种方法各有所长，在解决问题的问题中，综合运用，效果会更好，综合法与分析法因其在解决问题中的作用巨大而受命题者的青睐，在历年的高考中均有体现，成为高考的重点和热点之一.※ 自我评价 你完成本节导学案的情况为（ ）. A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测（时量：5分钟 满分：10分）计分： 1. 给出下列函数①3y x x =-，②sin cos ,y x x x =+③sin cos ,y x x =④22,x x y -=+其中是偶函数的有（ ）.A ．1个B ．2个C ．3 个D ．4个2. m 、n 是不同的直线，,,αβγ是不同的平面，有以下四个命题（ ）. ①//////αββγαγ⎧⇒⎨⎩ ；②//m m αββα⊥⎧⇒⊥⎨⎩ ③//m m ααββ⊥⎧⇒⊥⎨⎩ ；④////m nm n αα⎧⇒⎨⊂⎩其中为真命题的是 （ ）A ．①④ B. ①③ C ．②③ D ．②④3. 下列结论中，错用基本不等式做依据的是（ ）. A ．a ，b 均为负数，则2a b ba+≥B 22≥C ．lg log 102x x +≥D ．1,(1)(1)4a R a a+∈++≥4. 设α、β、r 是互不重合的平面，m ，n 是互不重合的直线，给出四个命题：①若m⊥α，m⊥β，则α∥β ②若α⊥r，β⊥r，则α∥β③若m⊥α，m∥β，则α⊥β ④若m∥α，n⊥α，则m⊥n5. 已知:23)0p <, 则p 是q 的 条件.1. 已知,,a b c R +∈，,,a b c 互不相等且1abc =.111a b c<++.2. 已知,,,a b c d 都是实数，且22221,1a b c d +=+=，求证：||1ac bc +≤.。

§2.2 直接证明与间接证明 2．2.1 综合法和分析法(一)课时目标 1.了解直接证明的两种基本方法——分析法和综合法.2.理解分析法和综合法的思考过程、特点，会用分析法和综合法证明数学问题．综合法分析法定义利用__________和某些数学______、______、______等，经过一系列的____________，最后推导出所要证明的结论成立，这种证明方法叫做综合法从要证明的______，逐步寻求使它成立的____________，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、______、______、______等)，这种证明方法叫做分析法框图表示 P ⇒Q 1→Q 1⇒Q 2→Q 2⇒Q 3→…→Q n ⇒Q (P 表示________、已 有的______、______、 ______等，Q 表示 ________________) Q ⇐P 1→P 1⇐P 2→ P 2⇐P 3→…→ 得到一个明显成立的条件特点顺推证法或由因导果法逆推证法或执果索因法一、选择题1．已知x ≥52，则f (x )＝x 2－4x ＋52x －4有( )A ．最大值54B ．最小值54C ．最大值1D ．最小值12．命题“对于任意角θ，cos 4θ－sin 4θ＝cos 2θ”的证明：“cos 4θ－sin 4θ＝(cos 2θ－sin 2θ)(cos 2θ＋sin 2θ)＝cos 2θ－sin 2θ＝cos 2θ”过程应用了( )A ．分析法B ．综合法C ．综合法、分析法综合使用D ．间接证法3．如果x >0，y >0，x ＋y ＋xy ＝2，则x ＋y 的最小值是( )A ．32B ．23－2C ．1＋ 3D ．2－ 34．要证明a ＋a ＋7<a ＋3＋a ＋4 (a ≥0)可选择的方法有多种，其中最合理的是( )A ．综合法B ．类比法C ．分析法D ．归纳法5．已知实数a ，b ，c 满足a ＋b ＋c ＝0，abc >0，则1a ＋1b ＋1c的值( )A ．一定是正数B ．一定是负数C ．可能是零D ．正、负不能确定二、填空题6．设a ＝3＋22，b ＝2＋7，则a 、b 的大小关系为________．7．已知a 、b 、u ∈R *，且1a ＋9b＝1，则使得a ＋b ≥u 恒成立的u 的取值范围是__________．8．设a ＝2，b ＝7－3，c ＝6－2，则a ，b ，c 的大小关系为__________．三、解答题9．已知a >0，b >0，求证：b 2a ＋a 2b≥a ＋b .10．已知a ，b ，c ，d ∈R ，求证：ac ＋bd ≤(a 2＋b 2)(c 2＋d 2).能力提升11．a >b >c ，n ∈N *，且1a －b ＋1b －c ≥na －c恒成立，则n 的最大值为________．12．已知a >0，b >0，用两种方法证明：a b ＋ba≥a ＋b .1．运用综合法解题时，要保证前提条件正确，推理要合乎逻辑规律，只有这样才能保证结论的正确性．2．在分析法证明中，从结论出发的每一个步骤所得到的判断都是使结论成立的充分条件．最后一步归结到已被证明了的事实．因此，从最后一步可以倒推回去，直到结论，但这个倒推过程可以省略．§2.2 直接证明与间接证明 2．2.1 综合法和分析法(一)答案综合法 分析法定利用已知条件和某些数学定义、定理、从要证明的结论，逐步寻求使它成立的充分条1．D [f (x )＝x －22＋12(x －2)∵x －2≥12，∴f (x )≥2·x －22×12(x －2)＝1.当x ＝3时，f (x )min ＝1.]2．B [从证明的过程来看是从已知条件入手经过推导得到结论，符合综合法．] 3．B [由x >0，y >0，x ＋y ＋xy ＝2，则2－(x ＋y )＝xy ≤⎝⎛⎭⎫x ＋y 22， ∴(x ＋y )2＋4(x ＋y )－8≥0，∴x ＋y ≥23－2或x ＋y ≤－2－2 3.∵x >0，y >0，∴x ＋y 的最小值为23－2.] 4．C [要证a ＋a ＋7<a ＋3＋a ＋4， 只要证a ＋a ＋7＋2a (a ＋7) <a ＋3＋a ＋4＋2(a ＋3)(a ＋4)， 只要证a 2＋7a <a 2＋7a ＋12， 只要证a 2＋7a <a 2＋7a ＋12， 只要证0<12.由此可知，最合理的是分析法．]5．B [∵a ＋b ＋c ＝0，∴(a ＋b ＋c )2＝0， ∴a 2＋b 2＋c 2＋2(ab ＋bc ＋ac )＝0，∴ab ＋bc ＋ac ＝－12(a 2＋b 2＋c 2)<0.又abc >0，∴1a ＋1b ＋1c ＝ab ＋bc ＋acabc<0.]6．a <b解析 a ＝3＋22，b ＝2＋7两式的两边分别平方，可得a 2＝11＋46，b 2＝11＋47，明显6<7，故a <b .7．(－∞，16]解析 ∵a ＋b ＝(a ＋b )⎝⎛⎭⎫1a ＋9b＝10＋b a ＋9a b ≥10＋2b a ×9a b ＝16，当且仅当b a ＝9ab即3a ＝b 时取等号，若a ＋b ≥u 恒成立，则u ≤16. 8．a >c >b解析 b ＝47＋3，c ＝46＋2，显然b <c . 而a 2＝2，c 2＝8－212＝8－48 <8－36＝2＝a 2， ∴a >c .9．证明 ∵b 2a ＋a 2b ＝a 3＋b3ab＝(a ＋b )(a 2－ab ＋b 2)ab，又∵a >0，b >0，∴a 2－ab ＋b 2－ab ＝(a －b )2≥0，∴a 2－ab ＋b 2≥ab ，∴a 2－ab ＋b 2ab≥1，∴(a ＋b )·a 2－ab ＋b 2ab≥a ＋b .∴b 2a ＋a 2b≥a ＋b . 10．证明 ①当ac ＋bd ≤0时，显然成立． ②当ac ＋bd >0时，欲证原不等式成立， 只需证(ac ＋bd )2≤(a 2＋b 2)(c 2＋d 2)．即证a 2c 2＋2abcd ＋b 2d 2≤a 2c 2＋a 2d 2＋b 2c 2＋b 2d 2. 即证2abcd ≤b 2c 2＋a 2d 2. 即证0≤(bc －ad )2.因为a ，b ，c ，d ∈R ，所以上式恒成立． 故原不等式成立，综合①、②知，命题得证． 11．4解析 ∵a >b >c ，∴a －b >0，b －c >0，a －c >0.若1a －b ＋1b －c ≥n a －c 恒成立， 即a －c a －b ＋a －c b －c≥n 恒成立． a －c a －b ＋a －c b －c ＝a －b ＋b －c a －b ＋a －b ＋b －cb －c ＝2＋b －c a －b ＋a －b b －c ≥2＋2b －c a －b ·a －b b －c ＝4.∴当且仅当a －b ＝b －c 时取等号． ∴n 的最大值为4.12．证明 方法一 (综合法)： 因为a >0，b >0，所以a b ＋ba －a －b＝⎝⎛⎭⎫a b －b ＋⎝⎛⎭⎫ba －a ＝a －b b ＋b －aa＝(a －b )⎝⎛⎭⎫1b －1a＝(a －b )2(a ＋b )ab ≥0，所以a b ＋ba≥a ＋b .方法二(分析法)：要证ab＋ba≥a＋b，只需证a a＋b b≥a b＋b a，即证(a－b)(a－b)≥0，因为a>0，b>0，a－b与a－b同号，所以(a－b)(a－b)≥0成立，所以ab＋ba≥a＋b成立．。

栏目 导引
第二章 推理与证明
2.要证明 3＋ 7<2 5可选择的方法有以下几
种，其中最合理的是( )
A．综合法
B．分析法
C．类比法
D．归纳法
解析：选B.从数据来看，宜用分析法．
栏目 导引
第二章 推理与证明
典题例证技法归纳
题型探究 题型一 综合法的应用
例1 已知 x＋y＋z＝m.求证：x2＋y2＋z2≥m32.
栏目 导引
第二章 推理与证明
即证 a2＋b2≥12(a2＋b2＋2ab)， 即证 a2＋b2≥2ab.6 分 ∵a2＋b2≥2ab 对一切实数恒成立.7 分 ∴ a2＋b2≥ 22(a＋b)成立.8 分师微博 平时练习时，这一步你想到、做到了吗？ 【名师点评】 应用分析法证明问题的模式 (若p则q形式)如下： 为了证明命题q为真， 只需证命题p1为真，从而有…… 只需证命题p2为真，从而有…… …… 只需证明命题p为真，而已知p为真，故q必为 真．
栏目 导引
第二章 推理与证明
即 （x－1）（x－4）< （x－3）（x－2）， 只需证[ （x－1）（x－4）]2<[ （x－3）（x－2）]2， 即证 x2－5x＋4<x2－5x＋6，即 4<6， 这显然成立． ∴当 x≥4 时， x－1－ x－2< x－3－ x－4.
栏目 导引
第二章 推理与证明
这种证明方法叫做综合法 __定__义___、__公__理___等)，这
种证明方法叫做分析法
栏目 导引
综合法
P⇒Q1 →
Q1⇒Q2 →
框
Q2⇒Q3 →…→ Qn⇒Q
图
表 (P表示_已__知__条__件____、已有
示 的__定__义___、__公__理___、 __定__理____等，Q表示

2.2直接证明
1
2.2.1 综合法和分析法
2
教学目标
结合已经学过的数学实例，了解直接证明的两 种基本方法：分析法和综合法；了解分析法和 综合法的思考过程、特点. 教学重点：会用综合法分析法证明问题；了解 综合法分析法的思考过程. 教学难点：根据问题的特点，结合综合法和分 析法的思考过程、特点，选择适当的证明方法
练习1:已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc 证明: 因为b2+c2 ≥2bc,a>0
所以a(b2+c2)≥2abc.
又因为c2+a2
≥2ac,b>0
所以b(c2+a2)≥ 2abc. 因此a(b2+c2)+b(c2+a2)≥4abc. 练习2:课本P9
【思维总结 】 2．综合法证明不等式所依赖的主要是不等式的基本性
因为;( a b ) 2 0 成立
a+b 所以 2
a+b ab 成立 所以 2 ab成立
如图所示，已知BE，CF分别为△ABC的边AC， AB上的高，G为EF的中点，H为BC的中点。 A 求证：HG⊥EF 证明：考虑待证的结论 F G E “HG⊥EF” 根据命题的条件：G是EF的中点， 连接EH,FH, 只要证明△EHF为等腰三角形，即 B C H EH=HF 根据条件CF⊥AB，且H是BC的中点，可知Rt△BCF斜 边上的中线
1 所以 BM AC 2 1 同理 DM AC 2
变式1
这样就证明了△BMD为等腰三角形
所以 MN ⊥ BD
引例2
a 3 b 3 a 2b ab 2 已知a, b R , 且a b, 求证 :

2.2.1(二)
2.2.1
【学习要求】
本 课 时 栏 目 开 关
综合法和分析法(二)
加深对综合法、分析法的理解，应用两种方法证明数学问 题． 【学法指导】 通过本节课的学习，比较两种证明方法的优点，进而灵活 选择证明方法，规范证明步骤，养成言之有理、论之有据 的好习惯，提高思维能力.
试一试· 双基题目、基础更牢固
也就是证明 2 a＋2 b＋2 c<2bc＋2ac＋2ab. 因为 a、b、c 为互不相等的正数且 abc＝1， 所以 bc ＋ ac>2 abc2 ＝ 2 c ； ac ＋ ab>2 a2bc ＝ 2 a ； ab ＋ bc>2 ab2c＝2 b；
相加得 2 a＋2 b＋2 c<2bc＋2ac＋2ab. 所以，原不等式成立．
2.2.1(二)
跟踪训练 3 如图，正方形 ABCD 和四边形 ACEF 所在的平面互相垂直，EF∥AC，AB＝ 2，CE＝EF＝1. (1)求证：AF∥平面 BDE；
本 课 时 栏 目 开 关
(2)求证：CF⊥平面 BDE.
证明 (1)如图，设 AC 与 BD 交于点 G. 1 因为 EF∥AG，且 EF＝1，AG＝ AC＝1， 2 所以四边形 AGEF 为平行四边形．
研一研· 题型解法、解题更高效
2.2.1(二)
题型二 例2
选择恰当的方法证明等式
已知△ABC 的三个内角 A，B，C 成等差数列，对应 1 1 3 的三边为 a，b，c，求证： ＋ ＝ . a＋b b＋c a＋b＋c
本 课 时 栏 目 开 关
a＋b＋c a＋b＋c 证明 要证原式，只需证 ＋ ＝3， a＋b b＋c c a 即证 ＋ ＝1， a＋b b＋c bc＋c2＋a2＋ab 即只需证 ＝1， 2 ab＋b ＋ac＋bc

证法1:对于正数a,b, 有
（ a
2 b ） ≥0
证法2:要证 ab ≤ a b 2 只要证 2 ab ≤ a b 只要证 0 ≤ a 2 ab b
2 0 ≤ ( a b ) 只要证
a b 2 ab ≥ 0 a b ≥ 2 ab ab ≥ 2 ab
只需证a
而
a b b b a a b 0
a ( a b ) b( a b ) ( a b )( a b ) 2 0
a b b 2 a ， a 2 b 所以 b a
当且仅当a=b时取等号
当且仅当 a=b 成立 所以
a b a b成立 b a
(a+b)(a2 ab b2 ) ab(a b)
即 a3 b3 a2b ab2 ， 所以命题得证.
（变式练习）
1 1. 若a 0, b 0, 求证：a b 2 2. ab
ab 2. 若 a 1, b 1, 求证： 1. 1 ab
直接证明
1 概念 直接从原命题的条件逐步推得命题成立 2 直接证明的一般形式：
本题条件 已知定义 本题结论 已知公理 已知定理
引例一:证明不等式: x2 2 2 x( x R) 证法1:由 x2 2 2 x ( x 1)2 1 1 0 x2 2 2 x 2 ( x 1) 0 ( x 1)2 1 1 0 证法2:由
分析：由A，B，C成等差数列可得什么？
由a，b，C成等比数列可得什么？
怎样把边，角联系起来？ 点评：解决数学问题
文字语言
时，学会语言转换； 还要细致，找出隐含 条件。
图形语言

分析法 又叫逆推证法或执果索 . , 因法
用Q表示要证明的结论 则分析法可用框图表示 : , 为
Q P1
P1 P2
P2 P3

得到一个明显 成立的条件
例 2 如图 2.2 1 所示 , SA 平面ABC, AB BC, 过A作SB 的垂线, 垂足为E , 过E作SC的 垂线, 垂足为F.求证 AF SC.
a,b, c成等比数列转化为符号语言就是 ac. , b 此时,如果能把角和边统一起 ,那么就可以进一 来 步寻找角和边之间的关 , 进而判断三角形的形 系 状, 余弦定理正好满足要求 .于是,可以用余弦定理 为工具进行证明 .
2
证明 由A,B, C成等差数列有2B A C. , 因为A,B, C为ΔABC的内角 所以A B C π. , π 由 ① ②, 得B . 3 2 由a,b, c成等比数列有b ac. ,


1 即证 cos α sin α cos2 β sin2 β , 2 1 2 即证1 2 sin α 1 2 sin2 β , 2 即证4 sin2 α 2 sin2 β 1.
2 2




由于上式与③ 相同,于是问题得证.
用P表示已知条件定义、定 理、公理 等 , 用Q 表示要证明的结论 则上述过 , 程可用框图表示为:
π 例3 已知α, β kπ k Z , 且 2 sin θ cos θ 2 sin α , ① sin θ cos θ sin β ,
2 2 2
②
1 tan α 1 tan β 求证 : . 2 2 1 tan α 2 1 tan β

-16-
2.2.1 综合法与分析法
探究一
探究二
探究三
课前篇自主预习 课课堂堂篇篇探探究究学学习习 规范解答 当堂检测
综合法与分析法的综合应用 例3已知a、b、c是不全相等的正数,且0<x<1.
求证:logx������+2������+logx������+2 ������+logx������+2 ������<logxa+logxb+logxc. 分析:解答本题的关键是利用对数运算法则和对数函数性质将题 目转化成整式不等式证明.
①综合法的特点是从“已知”看“未知”,其逐步推理实际上是寻找
已知条件的必要条件.
②综合法从命题的条件出发,利用定义、公理、定理和运算法则,
通过演绎推理,一步一步完成命题的证明.
-3-
2.2.1 综合法与分析法
课前篇自主预习 课堂篇探究学习
【做一做 1】 命题“求证:tan θ+ta1n������ = sin22������”的证明过程“tan
-17-
2.2.1 综合法与分析法
课前篇自主预习 课课堂堂篇篇探探究究学学习习
探究一
探究二
探究三
规范解答 当堂检测
解:要证明 logx������+2������+logx������+2 ������+logx������+2 ������<logxa+logxb+logxc,
只需要证明 logx
①分析法的特点是从“未知”看“需知”,逐步靠拢“已知”,其逐步推
理实际上是寻找使结论成立的充分条件.
②分析法从命题的结论入手,寻求结论成立的条件,直至归结为

1、 求 证 ： cos sin cos 2 2、 已 知 tan sin a , tan sin b 求 证： （a b ) 16ab
2 2 2
4
4
3、 已 知a , b, c R , a b c 1 1 1 1 求 证（ ： 1)( 1)( 1) 8 a b c
3 7 2 5成立
反思
在本例中，如果我们从“21<25”出发， 逐步倒推回去，就可以用综合法证出结论.但 由于我们很难想到从“21<25”入手，所以 用综合法比较困难.
• [点评] • (1)分析法证明不等式的依据是不等式的基本性质、 已知的重要不等式和逻辑推理的基本理论； • 2）分析法证明思路为：从求证的结论出发，逐步 寻求使结论成立的充分条件，直至把证明的结论 归结为一个明显成立的条件即可。 • (3) 用分析法证明数学命题时，一定要恰当地用好 “要证”、“只需证”、“即证”等关联词语．
a+b 练习：证明不等式： 2
ab
(a>0,b>0).
综合法
证法1:
因为;( a b ) 0
2
a+b 证法2:要证; ab 2 只需证;a + b 2 ab
分析法
所以 a + b 2 ab 0 所以 a + b 2 ab
a+b ab 成立 所以 2
只需证;a + b 2 ab 0

课堂小结
1.在数学证明中，综合法最常用的数学方法，若从已 知入手能找到证明的途径，则用综合法.
2.综合法的每步推理都是寻找必要条件，在解题表述 中要注意语言的规范性和逻辑性.

2．2直接证明与间接证明2．2.1综合法和分析法1．结合已经学习过的数学实例，了解直接证明的两种最基本的方法：综合法和分析法．2．了解用综合法和分析法解决问题的思考特点和过程，会用综合法和分析法证明具体的问题．通过实例充分认识这两种证明方法的特点，认识证明的重要性．基础梳理1．综合法．(1)定义：一般地，利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明的结论成立，这种证明方法叫做综合法．其一般表示形式是由因导果．(2)用P表示已知条件、已有的定义、定理、公理等，Q表示所要证明的结论，则综合法用框图表示为：P⇒Q1→Q1⇒Q2→Q2⇒Q3→…→Q n⇒Q2．分析法．(1)定义：一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直到最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)．这种证明的方法叫做分析法. 其一般表示形式是执果索因．(2)用Q表示要证明的结论，则分析法可用框图表示为：Q⇐P1→P1⇐P2→P2⇐P3→…→得到一个明显成立的条件3．分析综合法．(1)定义：根据条件的结构特点去转化结论，得到中间结论Q′；根据结论的结构特点去转化条件，得到中间结论P′.若由P′可以推出Q′成立，就可以证明结论成立．这种证明方法称为分析综合法．(2)用P表示已知条件、定义、定理、公理等，用Q表示要证明的结论，则分析综合法可用框图表示为：P⇒P1→P1⇒P2→…→P n⇒P′⇓Q m⇐Q′←…←Q1⇐Q2←Q⇐Q1基础自测1．设x，y∈R＋，且x＋y＝6，则lg x＋lg y的取值范围是(B)A．(－∞，lg 6]B．(－∞，2lg 3]C．[lg 6，＋∞) D．[2lg 3，＋∞)解析：∵x，y∈R＋，x＋y＝6，∴2xy≤6，即0＜xy≤9，∴lg xy ≤lg 9，即lg x＋lg y≤2lg 3.故选B.2．分析法又称执果索因法，若用分析法证明：“设a＞b＞c，且a＋b＋c＝0，求证：b2－ac＜3a”索的因应是(C)A．a－b＞0B．a－c＞0C．(a－b)(a－c)＞0D．(a－b)(a－c)＜0解析：b2－ac＜3a⇐b2－ac＜3a2⇐3a2＋ac－(a＋c)2＞0⇐(2a＋c)(a－c)＞0⇐(a－b)(a－c)＞0.故选C.3．已知f(x)＝x2，则f′(3)的值为__________________．解析：∵f(x)＝x2，∴f′(x)＝2x，∴f′(3)＝2×3＝6.答案：64．当a∈________时，函数f(x)＝x2－2(a－1)x＋3在[5，＋∞)上是增函数．解析：f(x)＝x2－2(a－1)x＋3在[5，＋∞)上是增函数⇐a－1≤5⇐a≤6.答案：(－∞，6]（一）综合法证题的基本步骤(1)分析题目的条件和结论，寻找已知与结论之间的有关数学公式、公理、定理、定义等，确定解决的初步思路；(2)整合所得信息进行推理论证，得出结论．（二）分析法证题的步骤以及格式欲证Q成立，只需证P1，即证P2，只需证P3，…，即证P，因为P成立，所以Q成立或运用逆向推理符号“⇐”，需要注意的是推理符号的方向，不可用反、用错．（三）分析综合法的综合应用在解决问题时，经常把综合法和分析法结合起来使用：用分析法找思路，用综合法写步骤．分析法与综合法相互转换、相互渗透、互为前提，充分利用这一辩证关系，注意它们的联合运用，可以增加解题思路，开阔视野．1．当所证结论与所给条件之间的关系不明确时，常采用分析法证明，但更多的时候是综合法与分析法结合起来使用，即先看条件能够提供什么，再看结论成立需要什么，从两头向中间靠拢，逐步接通逻辑思路．2．用分析法证题是寻求使结论成立的充分条件，不是必要条件，因此各步的寻求用“⇐”，有些步骤也可用“⇔”，但不能用“⇒”，因为是寻求充分条件，不必每步都是“⇔”，证完之后也不能说每步都可逆，只有证明充要条件时，才可以说每步都可逆，或全部都用“⇔”表达．3．综合法和分析法是直接证明中最基本的两种证明方法，也是解决数学问题时常用的思维方式．如果从解题的切入点的角度细分，直接证明方法可具体分为：比较法、代换法、放缩法、判别式法、构造函数法等．这些方法是综合法和分析法的延续与补充．1．“对于任意角θ，cos 4θ－sin 4θ＝cos 2θ ”的证明过程：“cos 4θ－sin 4θ＝(cos 2θ－sin 2θ)(cos 2θ＋sin 2θ)＝cos 2θ－sin 2θ＝cos 2θ”应用了(B )A ．分析法B ．综合法C ．综合法与分析法结合使用D ．演绎法 解析：这是由已知条件入手利用有关的公式证得等式，应用了综合法，故选B.2．要证明3＋5＜4，可选择的方法有以下几种，其中最合理的为(B )A ．综合法B ．分析法C ．比较法D ．归纳法解析：要证明3＋5<4，只需证明(3＋5)2<16，即8＋215<16，即证明15<4，亦即只需证明15<16，而15<16显然成立，故原不等式成立．因此利用分析法证明较为合理，故选B.3．已知a ＞0，b ＞0，m ＝lg a ＋b 2，n ＝lg a ＋b2，则m 与n的大小关系为________．解析：因为⎝ ⎛⎭⎪⎫a ＋b 22＝a ＋b ＋2ab 4＞⎝⎛⎭⎪⎫a ＋b 22， 所以a ＋b 2＞a ＋b 2.又因为y ＝lg x 为增函数，所以有m ＞n .答案：m ＞n4．如图，长方形ABCD-A1B1C1D1中，AB＝AA1＝1，AD＝2，E是BC的中点．(1)求证：直线BB1∥平面D1DE；(2)求证：平面A1AE⊥平面D1DE；(1)证明：在长方体ABCD-A1B1C1D1中，BB1∥DD1，又∵BB1⊄平面D1DE，DD1⊂平面D1DE，∴直线BB1∥平面D1DE.(2)证明：在长方形ABCD中，∵AB＝AA1＝1，AD＝2，∴AE＝DE＝ 2.∴AE2＋DE2＝4＝AD2，故AE⊥DE.∵在长方体ABCD-A1B1C1D1中，DD1⊥平面ABCD，AE⊂平面ACBD，∴DD1⊥AE.又∵DD1∩DE＝D，∴直线AE⊥平面D1DE.而AE⊂平面A1AE，所以平面A1AE⊥平面D1DE.1．设S n为等差数列{a n}的前n项和，若a1＝1，公差d＝2，S k＋－S k＝24，则k＝(D)2A．8 B．7 C．6 D．52．在三角形中，a为最大边，要想得到三角形为锐角三角形的结论，三边a，b，c应满足说明条件(A)A．a2＜b2＋c2B．a2＝b2＋c2C．a2＞b2＋c2D．a2≤b2＋c2解析：若三角形为锐角三角形，即∠A为锐角，由余弦定理知cos A＝b2＋c2－a22bc＞0，∴b2＋c2－a2＞0.3．设数列{a n}为等差数列，且a2＝－6，a8＝6，S n是{a n}的前n 项和，则(B)A．S4＜S5B．S4＝S5C．S6＞S5D．S6＝S5解析：∵a2＋a8＝－6＋6＝0，∴a5＝0，又公差d>0，∴S5＝S4.4．要使3a－3b＜3a－b成立，则a，b应满足的条件是(D)A．ab＜0且a＞bB．ab＞0且a＞bC．ab＜0且a＜bD．ab＜0且a＜b或ab>0且a>b解析：思路不明确，用分析法寻求使不等式成立的条件．3a－3b＜3a－b⇔a－b＋33ab2－33a2b＜a－b⇔3ab2＜3a2b，∴当ab＞0时，有3b＜3a，即b＜a；当ab＜0时，由3b＞3a，即b＞a.所以选D.5．已知a，b，c是三条互不重合的直线，α，β是两个不重合的平面，给出四个命题：①a∥b，b∥α，则a∥α；②a，b⊂α，a∥β，b∥β，则α∥β；③a⊥α，a∥β，则α⊥β；④a⊥α，b∥α，则a⊥b.其中正确命题的个数是(B)A．1 B．2 C．3 D．4解析：①因为a∥b，b∥α⇒a∥α或a⊂α，所以①不正确．②因为a，b⊂α，a∥β，b∥β，当a与b相交时，才能α∥β，所以②不正确．③α∥β，过a作一平面γ，设γ∩β＝c，则c∥a，又a⊥α⇒c ⊥α⇒α⊥β，所以③正确．④a ⊥α，b ∥α⇒a ⊥b ，所以④正确． 综上知③，④正确．6．a ＞0，b ＞0，则下列不等式中不成立的是(D )A ．A ＋B ＋1ab≥2 2 B ．(a ＋b )⎝ ⎛⎭⎪⎫1a ＋1b ≥4C.a 2＋b 2ab≥a ＋b D.2ab a ＋b ≥ab解析：特殊法，取a ＝1，b ＝4，则D 不成立．7．函数f (x )＝In 1－x1＋x，若f (a )＝b ，则f (－a )＝________．解析：因为f (－x )＝In 1＋x 1－x ＝In ⎝ ⎛⎭⎪⎫1－x 1＋x －1＝In 1－x 1＋x ＝－f (x )，所以f (－a )＝－f (a )＝－b .答案：－b8．设a ＝3＋7，b ＝2＋6，则a 、b 的大小关系为________．解析：由12＋3＞16＋7，化简得2－3＞7－ 6.从而2＋6＞3＋7，即a ＜b 答案：a ＜b9．p ＝ab ＋cd ，q ＝ma ＋nc ·b m ＋dn，(m ，n ，a ，b ，c ，d 均为正数)，则p 与q 的大小关系为________．解析：p 2＝ab ＋cd ＋2abcd ，q 2＝(ma ＋nc )⎝ ⎛⎭⎪⎫b m ＋d n＝ab ＋nbc m ＋madn＋cd≥ab ＋cd ＋2abcd ∴q 2≥p 2，∴p ≤q . 答案：p ≤q10．当x ∈(1，2)时，不等式x 2＋mx ＋4＜0恒成立，则m 的取值范围是________．解析：x 2＋mx ＋4＜0⇔m ＜－x －4x，∵y ＝－⎝ ⎛⎭⎪⎫x ＋4x 在(1，2)上单调递增，∴－⎝ ⎛⎭⎪⎫x ＋4x ∈(－5，－4)． ∴m ≤5.答案：(－∞，－5]11．在△ABC 中，三个内角A ，B ，C 对应的边分别为a ，b ，c ，且A ，B ，C 成等差数列，a ，b ，c 也成等差数列．求证：△ABC 为等边三角形．证明：由A ，B ，C 成等差数列知，B ＝π3，由余弦定理知b 2＝a 2＋c 2－ac ，又a ，b ，c 也成等差数列，∴b ＝a ＋c2.代入上式得（a ＋c ）24＝a 2＋c 2－ac ，整理得3(a －c )2＝0，∴a ＝c ，从而A ＝C ，而B ＝π3，则A ＝B ＝C ＝π3，从而△ABC 为等边三角形．12．如下图，在直三棱柱ABC -A 1B 1C 1中，E 、F 分别是A 1B ，A 1C 的中点，点D 在B 1C 1上，A 1D ⊥B 1C .求证：(1)EF ∥平面ABC ； (2)平面A 1FD ⊥平面BB 1C 1C .证明：(1)由E ，F 分别是A 1B ，A 1C 的中点知，EF ∥BC ， ∵EF ⊄平面ABC 而BC ⊂平面ABC . ∴EF ∥平面ABC . (2)由三棱锥ABC -A 1B 1C 1为直三棱柱知，CC 1⊥平面A 1B 1C 1，又A 1D ⊂平面A 1B 1C 1，∴A1D⊥CC1，又A1D⊥B1C.CC1∩B1C＝C，又CC1，B1C⊂平面BB1C1C，∴A1D⊥平面BB1C1C.又A1D⊂平面A1FD，∴平面A1FD⊥平面BB1C1C.►品味高考1．(2014·安徽高考)设a＝log3 7，b＝21.1，c＝0.83.1，则(B)A．b＜a＜c B．c＜a＜bC．c＜b＜a D．a＜c＜b解析：∵a＝log3 7，∴1＜a＜2.∵b＝21.1，∴b＞2.∵c＝0.83.1，∴0＜c＜1.故c＜a＜b，选B.π，c＝π－2，则(C) 2．(2014·天津高考)设a＝log2π，b＝log12A．a＞b＞c B．b＞a＞cC．a＞c＞b D．c＞b＞a解析：因为π＞2，所以a＝log2π＞1.因为π＞1，所以b＝log12π＜0.因为π＞1，所以0＜π－2＜1，即0＜c＜1.所以a＞c＞b.3．如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD.E和F分别是CD和PC的中点．求证：(1)PA⊥底面ABCD；(2)BE∥平面PAD；(3)平面BEF⊥平面PCD.证明：(1)∵平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，∴PA⊥底面ABCD.(2)∵AB∥CD，CD＝2AB，E为CD的中点，∴AB∥DE，且AB＝DE.∴ABDE为平行四边形．∴BE∥AD.又∵BE⊄平面PAD.∴BE∥平面PAD.(3)∵AB⊥AD，而且ABED为平行四边形，∴BE⊥CD，AD⊥CD.由(1)知PA⊥底面ABCD.∴PA⊥CD.又AD∩PA＝A，∴CD⊥平面PAD.∴CD⊥PD.∵E和F分别是CD和PC的中点，∴PD∥EF.∴CD⊥EF.∴CD⊥平面BEF.∴平面BEF⊥平面PCD.。

sin( 2 ) cos( 2 ) cos( 2 ) sin( 2 )

3.
即 tan( 2 ) cot( 2 ) 3.
说明
综合法证题步骤： P0 （已知） P P2 Pn 1 （结论） .
综合法 直接证明
A D C B
求证：当一个圆与一个正方形的周长 相等时，这个圆的面积比正方形的面积大
3．小结： 分析法和综合法是思维方向相反的两种 思考方法。在数学解题中，分析法是从数 学题的待证结论或需求问题出发，一步一 步地探索下去，最后达到题设的已知条件。 综合法则是从数学题的已知条件出发，经 过逐步的逻辑推理，最后达到待证结论或 需求问题。对于解答证明来说，分析法表 现为执果索因，综合法表现为由因导果， 它们是寻求解题思路的两种基本思考方法， 应用十分广泛。
证明: 要证 只需证
a -5 - a -3 < a -2 - a a -5 a < a -2 + a -3
a(a - 5) < (a - 2)(a - 3)
只需证 只需证
因为 所以
a(a - 5)<(a - 2)(a - 3)
0<6
成立. 成立.
a -5 - a -3 < a -2 - a
小结
c.
abc 2 +
ab 2c = a + b + 1 1 1 ∴ a + b + c < + + 成立. a b c a 2 bc +
课堂 练习
1. 已知 8 cos( 2 ) 5 cos 0 ， 求证 tan( ) tan 13 3 .

§2.2.1 综合法和分析法(二) 学习目标.2. 根据问题的特点，结合分析法的思考过程、特点，选择适当的证明方法. 学习过程一、课前准备4850复习1：综合法是由 导 ;复习2：基本不等式:二、新课导学※ 学习探究探究任务一：分析法问题：如何证明基本不等式(0,0)2a b ab a b +≥>>新知：从要证明的结论出发，逐步寻找使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止.反思：框图表示要点：逆推证法；执果索因※ 典型例题例13526变式：求证3725小结：证明含有根式的不等式时,用综合法比较困难,所以我们常用分析法探索证明的途径.例2 在四面体S ABC -中,,SA ABC AB BC ⊥⊥面,过A 作SB 的垂线,垂足为E ,过E 作SC 的垂线,垂足为F ,求证AF SC ⊥.变式：设,,a b c 为一个三角形的三边,1()2s a b c =++,且22s ab =,试证2s a <.小结：用题设不易切入,要注意用分析法来解决问题.※动手试试练1. 求证:当一个圆和一个正方形的周长相等时,圆的面积比正方形的面积大.练2. 设a, b, c是的△ABC三边，S是三角形的面积，求证：2224--+≥c a b ab三、总结提升※学习小结,P P⋅⋅⋅，直到所有的分析法由要证明的结论Q思考，一步步探求得到Q所需要的已知12,已知P都成立.※知识拓展证明过程中分析法和综合法的区别:在综合法中,每个推理都必须是正确的,每个推论都应是前面一个论断的必然结果,因此语气必须是肯定的.分析法中,首先结论成立,依据假定寻找结论成立的条件，这样从结论一直到已知条件.※ 自我评价 你完成本节导学案的情况为（ ）.A. 很好B. 较好C. 一般D. 较差※ 当堂检测（时量：5分钟 满分：10分）计分：1. ,其中最合理的是A.综合法B.分析法C.反证法D. 归纳法2.不等式①233x x +>;②2b a a b+≥,其中恒成立的是 A.① B.② C.①② D.都不正确3.已知0y x >>,且1x y +=,那么A.22x y x y xy +<<<B.22x y xy x y +<<< C.22x y x xy y +<<< D.22x y x xy y +<<< 4.若,,a b c R ∈,则222a b c ++ ab bc ac ++.5.将a 千克的白糖加水配制成b 千克的糖水(0)b a >>,则其浓度为 ;若再加入m 千克的白糖(0)m >,糖水更甜了,根据这一生活常识提炼出一个常见的不等式: .1. 已知0a b >>,求证:22()()828a b a b a b a b-+-<.2. 设,a b R +∈,且a b ≠,求证:3322a b a b ab +>+。

数学：2.2.1《综合法和分析法》教案教学目标：<一）知识与技能：结合已经学过的数学实例，了解直接证明的两种基本方法：分析法和综合法；了解分析法和综合法的思考过程、特点。

<二）过程与方法:培养学生的辨析能力和分析问题和解决问题的能力；<三）情感、态度与价值观：通过学生的参与，激发学生学习数学的兴趣。

第一课时 2.2.1 综合法和分析法<一）教学要求：结合已经学过的数学实例，了解直接证明的两种基本方法：分析法和综合法；了解分析法和综合法的思考过程、特点.tFAx82mkCG教学重点：会用综合法证明问题；了解综合法的思考过程.教学难点：根据问题的特点，结合综合法的思考过程、特点，选择适当的证明方法.教学过程：一、复习准备：1. 已知“若，且，则”，试请此结论推广猜想.<答案：若，且，则）2. 已知，，求证：.先完成证明→ 讨论：证明过程有什么特点？二、讲授新课：1. 教学例题：① 出示例1：已知a, b, c是不全相等的正数，求证：a(b2 + c2> + b(c2 + a2> + c(a2 + b2> > 6abc.tFAx82mkCG分析：运用什么知识来解决？<基本不等式）→ 板演证明过程<注意等号的处理）→ 讨论：证明形式的特点② 提出综合法：利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明的结论成立.tFAx82mkCG框图表示：要点：顺推证法；由因导果.③ 练习：已知a，b，c是全不相等的正实数，求证.④ 出示例2：在△ABC中，三个内角A、B、C的对边分别为a、b、c，且A、B、C成等差数列，a、b、c成等比数列. 求证：为△ABC 等边三角形.tFAx82mkCG分析：从哪些已知，可以得到什么结论？如何转化三角形中边角关系？→ 板演证明过程→ 讨论：证明过程的特点.→ 小结：文字语言转化为符号语言；边角关系的转化；挖掘题中的隐含条件<内角和）2. 练习：①为锐角，且，求证：. <提示：算）② 已知求证：3. 小结：综合法是从已知的P出发，得到一系列的结论，直到最后的结论是Q. 运用综合法可以解决不等式、数列、三角、几何、数论等相关证明问题.tFAx82mkCG三、巩固练习：1. 求证：对于任意角θ，. <教材P100 练习 1题）<两人板演→ 订正→ 小结：运用三角公式进行三角变换、思维过程）2. 的三个内角成等差数列，求证：.3. 作业：教材P102 A组 2、3题.第二课时 2.2.1 综合法和分析法<二）教学要求：结合已经学过的数学实例，了解直接证明的两种基本方法：分析法和综合法；了解分析法和综合法的思考过程、特点.tFAx82mkCG教学重点：会用分析法证明问题；了解分析法的思考过程.教学难点：根据问题的特点，选择适当的证明方法.教学过程：一、复习准备：1. 提问：基本不等式的形式？2. 讨论：如何证明基本不等式.<讨论→ 板演→ 分析思维特点：从结论出发，一步步探求结论成立的充分条件）二、讲授新课：1. 教学例题：① 出示例1：求证.讨论：能用综合法证明吗？→ 如何从结论出发，寻找结论成立的充分条件？→ 板演证明过程 <注意格式）→ 再讨论：能用综合法证明吗？→ 比较：两种证法② 提出分析法：从要证明的结论出发，逐步寻找使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件<已知条件、定理、定义、公理等）为止.tFAx82mkCG框图表示：要点：逆推证法；执果索因.③ 练习：设x > 0，y > 0，证明不等式：.先讨论方法→ 分别运用分析法、综合法证明.④ 出示例2：见教材P97. 讨论：如何寻找证明思路？<从结论出发，逐步反推）⑤ 出示例3：见教材P99. 讨论：如何寻找证明思路？<从结论与已知出发，逐步探求）2. 练习：证明：通过水管放水，当流速相等时，如果水管截面<指横截面）的周长相等，那么截面的圆的水管比截面是正方形的水管流量大.tFAx82mkCG提示：设截面周长为l，则周长为l的圆的半径为，截面积为，周长为l的正方形边长为，截面积为，问题只需证：> .tFAx82mkCG3. 小结：分析法由要证明的结论Q思考，一步步探求得到Q所需要的已知，直到所有的已知P都成立；比较好的证法是：用分析法去思考，寻找证题途径，用综合法进行书写；或者联合使用分析法与综合法，即从“欲知”想“需知”(分析>，从“已知”推“可知”<综合），双管齐下，两面夹击，逐步缩小条件与结论之间的距离，找到沟通已知条件和结论的途径. <框图示意）tFAx82mkCG三、巩固练习：1. 设a, b, c是的△ABC三边，S是三角形的面积，求证：.略证：正弦、余弦定理代入得：，即证：，即：，即证：<成立）.2. 作业：教材P100 练习 2、3题.第三课时 2.2.2 反证法教学要求：结合已经学过的数学实例，了解间接证明的一种基本方法——反证法；了解反证法的思考过程、特点.教学重点：会用反证法证明问题；了解反证法的思考过程.教学难点：根据问题的特点，选择适当的证明方法.教学过程：一、复习准备：1. 讨论：三枚正面朝上的硬币，每次翻转2枚，你能使三枚反面都朝上吗？<原因：偶次）2. 提出问题：平面几何中，我们知道这样一个命题：“过在同一直线上的三点A、B、C不能作圆”. 讨论如何证明这个命题？tFAx82mkCG3. 给出证法：先假设可以作一个⊙O过A、B、C三点，则O在AB的中垂线l上，O又在BC的中垂线m上，即O是l与m的交点。