热学玻尔兹曼分布.ppt

Physical Chemistry(下册）物理化学（下册）第七章电化学第九章化学动力学第八章界面现象第十章胶体化学第十一章统计热力学物理化学（下）绪论第十一章统计热力学Chapter 11 Statistical thermodynamics§11-！本章基本要求§11-1统计热力学基本概念及术语§11-2能级分布的微态数及系统的总微态数§11-3最可几分布、平衡分布、玻尔兹曼分布及配分函数定义§11-4粒子配分函数的计算§11-5系统内能热容与配分函数的关系§11-6系统熵与配分函数的关系§11-7其它热力学函数与配分函数的关系§11-8理想气体反应标准平衡常数与配分函数的关系§11-$本章小结与学习指导一、概率二、等概率定理三、最概然分布四、最概然分布与平衡分布五、最概然分布推导六、粒子配分函数定义七、玻尔兹曼分布§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义1.概率若一个事件有多种可能则称为复合事件，各种可能出现的事件称为可能事件，或偶然事件。

复合事件重演m 次偶然事件A 出现n 次，当m趋于无穷大时，n/m 为定值，定义为事件A 出现的概率或称概然率，用PA表示。

一、概率§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义一、概率§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义在统计热力学中，系统的粒子数量级一般为1024左右，且粒子在不停的运动，碰撞频率极高，使系统微态不断变化。

在很短的时间内粒子经历的微态已足以反映出各种微态出现几率的稳定性。

即出现各微态的可能性与数学几率相符。

等概率定理：在（N、U、V）确定情况下，系统各微态出现的概率相等。

P=1/二、等概率定理§11-3最概然分布、平衡分布、玻尔兹曼分布及配分函数定义1.分布概率在（N、U、V）确定时粒子的各种分布D的微态数ωD不同，所以各种分布出现的几率不同。

玻尔兹曼分布玻尔兹曼分布律是一种覆盖系统各种状态的概率分布、概率测量或者频率分布。

当有保守外力（如重力场、电场等）作用时，气体分子的空间位置就不再均匀分布了，不同位置处分子数密度不同。

玻尔兹曼分布律是描述理想气体在受保守外力作用、或保守外力场的作用不可忽略时，处于热平衡态下的气体分子按能量的分布规律玻尔兹曼(L.E.Boltzmann)将麦克斯韦分布律推广到有外力场作用的情况。

在等宽的区间内，若E1>E2，则能量大的粒子数dN1小于能量小的粒子数dN2，状态即粒子优先占据能量小的，这是玻尔兹曼分布律的一个重要结果。

经过将近一个世纪的传播，物理学界、化学界渐渐接受了道尔顿的“原子—分子模型”，但原子、分子的确凿证据迟迟没有找到。

恰恰此时，一股更强大的科学成就——热力学第一、第二定律出现了。

热力学原则上解决了一切化学平衡的问题。

1892年，物理化学家奥斯特瓦尔德试图在此基础上证明，将物理学和化学问题还原为原子或分子之间的力学关系是多余的。

他试图将“能量”赋以实物一样的地位，甚至要把物质还原为能量。

他提出“世界上的一切现象仅仅是由于处于空间和时间中的能量变化构成的”。

在统计学中，麦克斯韦- 玻尔兹曼分布是一种特殊的概率分布，以詹姆斯·克拉克·麦克斯韦和路德维希·玻尔兹曼的名字命名。

它一开始在物理中定义并使用是为了描述（特别是统计力学中描述理想气体）在理想气体中粒子自由移动的在一个固定容器内与其它粒子无相互作用的粒子速度，除了它们相互或与它们的热环境交换能量与动量所产生的非常短暂的碰撞。

在这种情况下粒子指的是气态粒子（原子或分子），并且粒子系统被假定达到热力学平衡。

在这种分布最初从麦斯威尔1960年的启发性的基础上衍生出来时，玻尔兹曼之后对这种分布的物理起源进行了大量重要调查粒子速度概率分布指出哪一种速度更具有可能性：粒子将具有从分布中随机选择的速度，并且比其它选择方法更可能在速度范围内。

玻尔兹曼分布定律是覆盖系统各种状态的概率分布，概率测量或频率分布。

当存在保守的外力（例如重力场，电场等）时，气体分子的空间位置不再均匀分布，并且在不同位置分子数密度也不同。

玻尔兹曼分布定律描述了在保守外力或保守外力场的作用下处于热平衡状态的理想气体分子的能量分布。

L. E. Boltzmann将麦克斯韦分布定律扩展到外力场的情况。

在相同的宽度范围内，如果E1> E2，则能量DN1大的粒子的数量少于能量DN2小的粒子的数量，并且状态是粒子优先占据较小的能量，这是玻尔兹曼的重要结果分配法。

经过近一个世纪的传播，物理和化学界逐渐接受道尔顿的“原子分子模型”，但是原子和分子的确凿证据尚未得到发现。

这时，出现了更强大的科学成就，即热力学的第一定律和第二定律。

热力学原则上解决了化学平衡的所有问题。

1892年，物理化学家奥斯特瓦尔德（Ostwald）试图证明没有必要将物理和化学问题减少到原子或分子之间的机械关系。

他试图赋予“能量”与物质对象相同的状态，甚至使物质恢复能量。

他提出“世界上所有现象都仅由时空的能量变化构成”。

在统计中，麦克斯韦·玻尔兹曼分布是一种特殊的概率分布，以詹姆斯·克拉克·麦克斯韦和路德维希·玻尔兹曼的名字命名。

它首先被定义并在物理学中用于描述（特别是在统计力学中）粒子在理想气体中自由移动而不与固定容器中的其他粒子相互作用的速度，除了粒子与其热环境之间的非常短时间的碰撞之外通过交换能量和动力。

在这种情况下，粒子是指气态粒子（原子或分子），并且假定粒子系统达到了热力学平衡。

当这种分布最初是从1960年的麦克斯韦启蒙运动中获得的时，玻尔兹曼对这种分布的物理起源进行了许多重要的研究。

粒子速度的概率分布表明哪个速度更有可能：粒子具有从分布中随机选择的速度，并且比其他选择方法更有可能处于速度范围内。

分布取决于系统温度和颗粒质量。

Maxwell Boltzmann分布适用于经典理想气体，这是理想的真实气体。

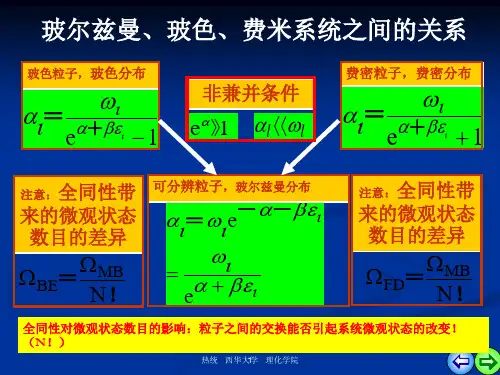
热辐射的研究可追溯至19世纪初，当时物理学家试图解释物体发出的热能。

其中，玻尔兹曼分布和玻色爱因斯坦模型在描述热辐射的能量分布和粒子行为方面发挥了重要作用。

1. 玻尔兹曼分布玻尔兹曼分布是描述理想气体中粒子速度分布的统计分布。

该分布表明，在平衡状态下，粒子的速度在不同方向上呈现高度的随机性和均匀性，这一主题在统计物理学和热力学中一直备受关注。

2. 玻色爱因斯坦模型玻色爱因斯坦模型则是描述玻色子（一类基本粒子）的行为模型，特别是在低温下的行为。

根据玻色爱因斯坦的统计推导，玻色子在低温下将呈现出玻色-爱因斯坦凝聚，形成所谓的Bose-Einstein凝聚态。

在探究这些概念的过程中，我们必须深入理解热辐射的性质和行为。

热辐射是指由物体散发的热量和光辐射，其性质由物体的温度和材料决定。

在低温下，热辐射的性质更倾向于玻色爱因斯坦模型所描述的玻色子行为，在高温下，将更符合玻尔兹曼分布的特性。

通过深入研究热辐射的性质和粒子行为，我们可以更好地理解热辐射的能量分布、粒子属性和统计规律。

这不仅有助于我们在物理学和热力学领域的研究，还对光子学、能源理论和材料科学等领域具有潜在的应用和发展前景。

在总结本文时，我们可以得出结论：热辐射是一个复杂而丰富的研究领域，涉及到物体的能量释放、粒子行为的统计规律等多个方面。

玻尔兹曼分布和玻色爱因斯坦模型为我们提供了对热辐射行为的重要理论支持，促使我们更深入地理解热辐射的本质和规律。

在个人观点方面，我认为热辐射的研究不仅有助于我们更好地理解自然界的现象，也为技术和应用的发展提供了重要的理论基础。

通过探索玻尔兹曼分布和玻色爱因斯坦模型，我们可以不断拓展对热辐射的认识，并在实践中应用这些理论，推动科学和技术的进步，创造更多的创新和发展机遇。

通过本文的阐述，我们深入探讨了热辐射、玻尔兹曼分布和玻色爱因斯坦模型等相关内容，希望能为您对这些主题的理解提供一定的启发和帮助。

在现代物理学领域，热辐射的研究一直是一个备受关注的话题。

在统计力学和数学中，玻尔兹曼分布（或吉布斯分布）是处于各种可能的微观量子状态下的粒子的概率分布，概率测度或频率分布。

具有以下形式，其中，量子态能量（随各个量子态而变化）和（对于玻尔兹曼分布是常数）是玻尔兹曼常数与热力学温度的乘积。

概率分布可以表示为，其中，量子态I的概率，量子态I的能量，玻尔兹曼常数，系统温度以及系统具有的量子态数。

对于两个状态的玻尔兹曼分布的比率，获得了玻尔兹曼因子。

可以看出，这仅与量子态之间的能量差有关。

玻尔兹曼分布取材于路德维希·博尔兹曼，他在1868年研究热平衡气体的统计力学时首次提出了这种分布。

然后在1902年，约西亚·威拉德·吉布斯提出了更为一般化的玻尔兹曼分布形式。

应特别注意Boltzmann分布与Maxwell-Boltzmann分布之间的差异。

前者给出了每个量子态中粒子的分布概率，而后者则用来描述理想气体中粒子的速度分布。

该表达在光谱学中具有重要的应用。

光谱中光谱线的位置表示粒子的量子态转移能量。

为了使谱线强度足够，必须有足够的处于高量子态的粒子。

因此，可以通过上述表达式确定颗粒分布与系统温度和能级差之间的关系，并且可以获得适当的系统参数。

统计力学的应用：玻尔兹曼分布可以应用于具有热平衡的隔离（或近似隔离）系统。

最常见的情况是常规合奏的概率分布，但在某些特殊情况下（源自常规合奏）也有相关应用。

数学的应用：在数学上，玻尔兹曼函数的广义形式是吉布斯测度。

在统计和机器学习中也称为对数线性模型。