奥林匹克训练题库·分割(word版)

杂题(二)训练 A卷班级______ 姓名______ 得分______1．计算:275×35+88×360+53×275+365×88=( )2．计算:44444×55555÷11111＝( )3．计算:999999×999999+1999999=( )4．全班42人排成一列横队。

从左面数起，小华是第24个，从右面数起，小明是第24个，小华和小明之间有( )人。

5．如果被乘数增加15，乘数不变、积就增加180。

如果被乘数不变，乘数增加4，那么积就增加12020来两个数相乘的积是( )。

6．有一个数自身相加、相减，相乘、相除，所得的结果的总和是81，这个数是( )。

7．把432个同样大小的正方形拼成一个长方形，一共有( )种不同的拼法。

8．把一个竹竿垂直插到一个蓄水池的池底，浸湿的部分是1.2米，掉过头把另一端垂直插到池底，这样没有浸湿的部分比全长的一半还少0.4米。

这根竹竿没有浸湿的部分长( )米。

9．小明在做减法时，把被减数十位上的8错看成3，把被减数个位上的5错看成6，这样算出来的差是108，正确的得数是( )。

10．有4个互不相等的自然数，最大数与最小数的差等于4，最小数与最大数的积是一个奇数，而这四个数的和是最小的两位奇数。

这四个数的积是多少？11．如果把一根长36厘米的铁丝围成长和宽都是整厘米数的长方形，一共有多少种围法？12．从1～9这九个数字中，每次取两个不同的数字组成一个两位数，而十位与个位上数字的和都必须比10大，这样的两位数一共有几个？13．有一块正方形木板，在它的第一边截去2分米，在相邻的第二边截去1分米，这样剩下部分的面积就比原来的少25平方分米，剩下的面积是多少平方分米？14．数一数下图中一共有( )个长方形(包括正方形)。

15．小明的妈妈买来一袋苹果和梨，已知苹果的只数是梨的2倍。

他们每天吃去5只苹果、4只梨。

质数、合数及质因数分解1可以分解为三个质数之积的最小的三位数是几？2用2，3，5，7四个数进行四则运算，每个数只能用一次，能够得到的最大质数是几？3“任何不小于4的偶数都可以表示为两个质数之和”，这就是著名的哥德巴赫猜想。

例如8=3+5，但是8只有这一种表示形式，而22却有3+19和5+17两种表示成两个不同质数之和的形式。

那么，能有两种表示成不同质数之和形式的最小自然数是几？4两个质数的和是39，求这两个质数的积。

5有两个质数，它们的和与差也都是质数，求这两个质数。

6A，B，C为三个质数，A+B=16，B+C=24，且A＜B＜C，求这三个质数。

7A，B，C为三个小于20的质数，A+B+C=30，且A＜B＜C，求这三个质数。

8除以9余2，并且与4和6的差都是质数的两位自然数有哪几个？9两个大于10的合数的和是31，求这两个数。

10将八个不同的合数填入下式的□中，如果要求相加的两个合数互质，那么A最小是几？A=□+□=□+□=□+□=□+□。

11将四个不同的合数分成两组，要求每组的两个合数之和都相等，而且每组的两个合数互质。

这四个合数之和最小可以是多少？12☆写出10个连续的自然数，它们个个都是合数。

13☆求不能用三个不相等的合数之和来表示的最大奇数。

14有一类多位数，各个数位上的数字都不相同，且相邻两个数位上的数字之和都是质数。

这类多位数中最大的是几？15有一类多位数，各个数位上的数字都不相同，且相邻两个数位上的数字之和都是合数。

这类多位数中最大的是几？16°两个连续奇数的乘积是111555，这两个奇数之和是多少？17°三个自然数的乘积为84，其中两个数的和等于另一个数。

求这三个数。

18°有7张卡片，上面分别写着1～7七个数字。

明明、芳芳和亮亮每人拿了2张。

明明说：“我的两张数字之和是7。

”芳芳说：“我的两张数字之差是1。

”亮亮说：“我的两张数字之积是12。

”那么，剩下的一张上面写的数字是几？19有1，2，3，4，5，6，7，8，9九张牌，甲、乙、丙各拿了三张。

奥林匹克训练题库第四章图形问题四立体图形体积与表面积1 将一个表面积为30cm2的正方体等分成两个长方体，再将这两个长方体拼成一个大长方体，求大长方体的表面积。

2 有30个边长为1m的正方体，在地面上摆成如右图所示的形式，然后把露出的表面涂成红色。

问：被涂成红色的表面积是多少？3 一个木盒从外面量，长、宽、高分别为10cm，8cm，5cm，木板厚1cm。

问：（1）做这个木盒至少需要1cm厚的木板多少平方厘米？（2）这个木盒的容积是多少？4 有大、中、小三个正方形水池，它们的内边长分别为4m，3m，2m，把两堆碎石分别沉没在中、小水池的水中，两个水池的水面分别升高了4cm和11cm，如果将这两堆碎石都沉没在大水池中，那么大水池水面将升高多少厘米？5 将表面积为54 cm2， 96 cm2， 150cm2的三个铁质正方体熔铸成一个大正方体（不计损耗）。

求这个大正方体的体积。

6 有一个棱长4cm的正方体，从它的右上方截去一个棱长分别为 4cm， 2cm，1cm的长方体（如左下图），求剩下部分的表面积。

7 求右上图所示（单位：cm）的机器零件的体积。

8 一个长方体，如果长增加2 cm，则体积增加 40cm3；如果宽增加 3 cm，则体积增加 90 cm3；如果高增加 4cm，则体积增加 96cm3。

求原长方体的表面积。

9 一个正方体被切成24个小长方体（见下图），这些小长方体的表面积总和为162cm2。

求这个正方体的体积。

10 把棱长分别为1cm，2cm，3cm的三个正方体的面胶合在一起（两个正方体胶合时，较小正方体的一个面必须全部胶合在较大正方体的面上），所得立体图形的表面积最大是多少？11 在棱长为3cm的正方体木块的每个面的中心上打一个直穿木块的洞，洞口呈边长为1cm的正方形（见右图）。

求挖洞后木块的体积及表面积。

12 左下图是由若干个小正方体组成的，阴影部分是空缺的通道。

问：这个立体图形由多少个小正方体组成？13 有一个棱长为 5 cm的正方体木块，从它的每个面看都有一个穿透的完全相同的孔（右上图），求这个立体图形的内、外表面的总面积。

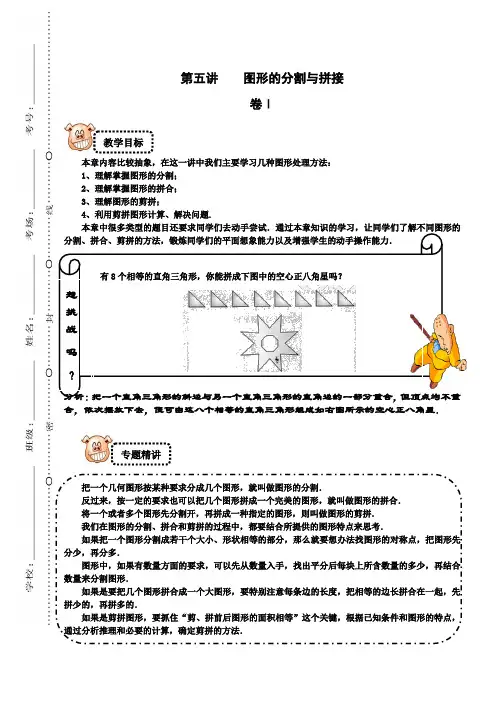
第五讲图形的分割与拼接卷Ⅰ教学目标本章内容比较抽象，在这一讲中我们主要学习几种图形处理方法：1、理解掌握图形的分割；2、理解掌握图形的拼合；3、理解图形的剪拼；4、利用剪拼图形计算、解决问题.本章中很多类型的题目还要求同学们去动手尝试．通过本章知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．有8个相等的直角三角形，你能拼成下图中的空心正八角星吗？想挑战吗？分析：把一个直角三角形的斜边与另一个直角三角形的直角边的一部分重合，但顶点均不重合，依次摆放下去，便可由这八个相等的直角三角形组成如右图所示的空心正八角星．专题精讲把一个几何图形按某种要求分成几个图形，就叫做图形的分割．反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．（一）图形的分割【例1】（★★★）把如右图这样由五个正方形组成的图形，分成四块大小、形状都相同的图形→→分析：从面积考虑，把整个图形的面积分成四份，分割后的每一部分占一份.正方形，则可把每个正方形分成四个面积相等的小正方形，每块图形应有五个这样的小正方形，如右上图所示.[前铺]如右图所示是由三个正方形组成的图形，请把它分成大小、形状都相同的四个图形？→→分析：要求把原来三个正方形分成四个大小、形状都相同的四个图形，先不考虑形状，大小相同也就是面积相等，也就是把整个图形的面积分成四份，分割后的每一部分占一份，可以考虑把每一个正方形的面积分成四份，再把三个正方形中的每一个小正方形合成要求的图形，如右上图所示.[巩固]右图是由五个正方形组成的图形．把它分成形状、大小都相同的四个图形，应怎样分?分析：如果不考虑分成的四个图形的形状，只考虑它们的面积，这就要求把原来五个正方形分成四个面积相等的图形，每个图形的面积应是1个多正方形．我们把每个正方形各分成四个面积相等的小正方形，分成的每块图形应有五个这样的小正方形．根据图形的对称性，我们很快就能得到如右上图的分法.【例2】（★★★★）怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.→分析：（1）分成8块的方法是：先取各边的中点并把它们连接起来，得到4个大小、形状相同的三角形，然后再把每一个三角形分成一半，得到如左上图所示的图形.（2）分成9块的方法是：先把每边三等分，然后再把分点彼此连接起来，得到加上右上图所示的符合条件的图形.[前铺]把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法．分析：根据等底等高的三角形面积相等这一结论，只要把原三角形分成4个等底等高的小三角形，它们的面积必定相等．而要得到这4个等底等高的小三角形，只需把原三角形的某条边四等分，再将各分点与这边相对的顶点连接起来就行了.根据上面的分析，可得如左上图所示的三种分法．又因为4＝l×4＝2×2，所以，如果我们把每一个小三角形的面积看做1，那么1×4就可以视为把三角形的面积直接分成4等份，即分成4个面积为1的小三角形；而2×2可以视为先把原三角形分成两等份，再把每一份分别分成两等份．根据前面的分析，在每次等分时，都要想办法找等底等高的三角形．根据上面的分析，又可以得到如右上图的另两种分法．【例3】（★★★★）如下图所示，请将这个正方形分切成两块，使得两块的形状、大小都相同，并且每一块都含有学而思奥数五个字.→图1 图2分析：图中有相同汉字挨在一起的情况，肯定要从它们之间切开（图1），因此，首先要在它们之间划出切分线.因为要将这个正方形切开成两块形状和大小都一样的图形，所以其中一块绕中心点旋转180°必定与另一块重合.要是把切分线也绕中心点旋转180°就可得到一些新的切分线（图2）.这就为我们解决问题提供了线索，本题的两种解法如上图所示.[拓展] 如右图所示的正方形是由36个小正方格组成的.如图那样放着4颗黑子，4颗白子，现在要把它切割成形状、大小都相同的四块，并使每一块中都有一颗黑子和一颗白子.试问如何切割？分析：首先在相同颜色的棋子之间划出切分线，以中心旋转90°、180°、270°之后，得一些新的切分线，同时考虑到每块包含有一颗黑子和一颗白子的要求，以及每一块面积应该是36÷4=9，即含有9个小正方格，先找到符合要求的一块后，让它绕中心旋转90°、180°、270°便得到其他三块，如右上图.【例4】如图，甲、乙是两个大小一样的正方形.要求把每一个正方形分成四块，两个正方形共分为八块，使每块的大小和形状都相同，而且都带一个○.分析：一个正方形分成大小和形状都相同的四块，一定是从中心点分开的，只要能找出其中符合题目要求的一块，然后再将这块绕着正方形的中心点分别旋转90°、180°、270°就可以得到另外三块.又因为这个正方形面积为36平方单位，所以分成的每一块的面积都是9平方单位.即每一块都由9个小正方格组成.另外，由于两个正方形要切分成一样大小的四块，因此可将两个正方形重叠在一起考虑.①将两个正方形重叠在一起，如右图所示，为便于区别，将其中一组的“○”改写成“×”.按要求将这重叠的正方形切分成大小、形状都相同的四块，并且每块都有一个“○”和“×”.②图中有相同符号的“○”挨在一起的从中间把它们切开，在它们中间划上截线.并将这些截线绕中心点旋转90°、180°、270°得到另外三段截线.如右图.利用它们设想出划分线.③设想分块从中心位置开始，逐步向外扩散，在里层方格中，先指定某一方格已分入到某小块中，并作上记号（斜线阴影），然后将它绕中心旋转180°后得到另一方格分入到另一小块中，也作上记号（横线阴影），如右图.对于中间一层方格和最外一层方格，设想分块时一定要紧扣条件：每一块中都要有一个“○”和一个“×”.每一块都有9个方格组成，不能断开.下图是分解了的分块过程示意图.④注意到斜线阴影部分已经有了一个“○”和一个“×”.那么左下角包含“○”的方格就不能再分到斜线阴影部分去了，而只能将右下角的方格分到斜线阴影部分.于是左上角的方格就应该分给横线阴影部分.空白部分是另外两块.右图就是最后分得的结果.（二）图形的拼合【例5】（★★★★）用6个完全一样的等腰直角三角形拼图，要求边与边完全重合．你能拼出几种图形?把它们画出来．分析：建议用等腰直角三角板，把不同的边进行重合，不要漏掉旋转重合，或者准备一些等腰直角三角形的纸片，由学生拼接后贴到黑板上，见下图[前铺]用3个等腰直角三角形拼图，要求边与边完全重合，能拼出几种图形?分析： 这种类型的题需要学生亲自操作，建议教师准备材料与学生互动。

最大与最小12在五位数 22576的某一位数码后面再插入一个该数码，能得到的六位数中最大的是几？13在六位数865473的某一位数码后面再插入一个该数码，能得到的七位数中最小的是几？14用1～8这八个数码组成两个四位数，要使这两个数的差尽量小，这个差是几？15要砌一个面积是72米2的长方形猪圈，长方形的边长都是自然数(单位∶米)，这个猪圈的围墙总长是多少米？16三个质数的和是100，这三个质数的积最大是几？17有一类自然数，它的各个数位上的数字之和为8888，这类自然数中最小的是几？18在下面的一排数字之间添上五个加号，组成一个连加算式，求这个连加算式的结果的最小值。

1 2 3 4 5 6 7 8 919把16拆成若干个自然数的和，要求这些自然数的乘积尽量大，应如何拆？202050拆成若干个自然数的和，要求这些自然数的乘积尽量大，应如何拆？21将30拆成若干个互不相同的自然数之和，要求这些自然数的乘积尽量大，应怎样拆？22将546分解成四个不同自然数的乘积，这四个自然数的和最大是多少？23三个两位的连续偶数，它们的个位数字的和能被7整除，这三个数的和最少等于多少？24有两个三位数，构成它们的六个数码互不相同。

已知这两个三位数之和等于1771，求这两个三位数之积的最大可能值。

25用1，3，5，7，9五个数码组成一个两位数和一个三位数，这两个数的乘积记为A；用0，2，4，6，8五个数码也组成一个两位数和一个三位数，这两个数的乘积记为B。

问:(1)(A－B)最大是多少？(2)(B - A)最大是多少？26有一类自然数，从第三个数字开始，每个数字都恰好是它前面两个数字之和，如246，1347等等，这类数中最大的自然数是几？27在下面的数表中，上、下两行都是等差数列。

上、下对应的两个数字中，大数减小数的差最小是几？28一个三位数的各位数字都不是0，这个三位数与组成它的各位数字之积的比是M(如三位数432，M=432÷(4×3×2)=18)，求 M的最大值。

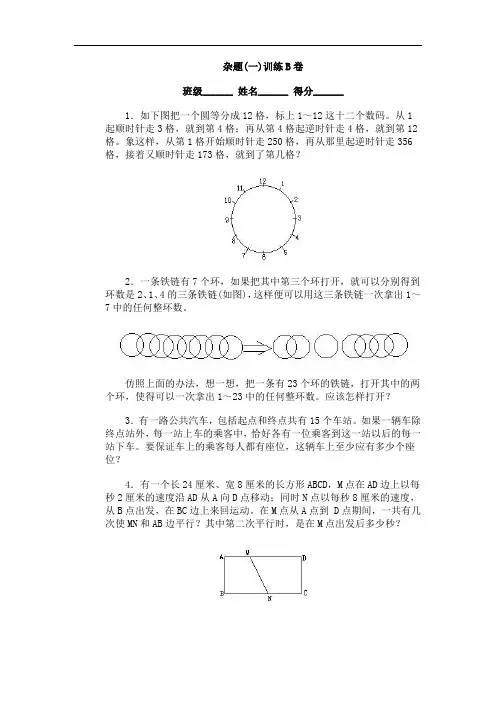
杂题(一)训练B卷班级______ 姓名______ 得分______1．如下图把一个圆等分成12格，标上1～12这十二个数码。

从1起顺时针走3格，就到第4格；再从第4格起逆时针走4格，就到第12格。

象这样，从第1格开始顺时针走250格，再从那里起逆时针走356格，接着又顺时针走173格，就到了第几格？2．一条铁链有7个环，如果把其中第三个环打开，就可以分别得到环数是2、1、4的三条铁链(如图)，这样便可以用这三条铁链一次拿出1～7中的任何整环数。

仿照上面的办法，想一想，把一条有23个环的铁链，打开其中的两个环，使得可以一次拿出1～23中的任何整环数。

应该怎样打开？3．有一路公共汽车，包括起点和终点共有15个车站。

如果一辆车除终点站外，每一站上车的乘客中，恰好各有一位乘客到这一站以后的每一站下车。

要保证车上的乘客每人都有座位，这辆车上至少应有多少个座位？4．有一个长24厘米、宽8厘米的长方形ABCD，M点在AD边上以每秒2厘米的速度沿AD从A向D点移动；同时N点以每秒8厘米的速度，从B点出发，在BC边上来回运动。

在M点从A点到 D点期间，一共有几次使MN和AB边平行？其中第二次平行时，是在M点出发后多少秒？5．甲乙两人在圆形跑道上从同一点A出发，按相反方向运动，他们的速度分别是每秒2米和每秒6米。

如果他们同时出发并当他们在A点第一次再相遇时为止，从出发到结束他们共相遇了几次？6．时针和分针在12点正重合，以后当他们第一次再重合时大约是什么时刻？7．工程师每天在同一时刻到达某站，然后乘上工厂定时来接的汽车按时到工厂。

有一天工程师提前55分钟到某站，因汽车未到就步行向工厂走去，在路上遇见来接他的汽车后乘车比平时提前10分钟到达工厂。

已知汽车每小时行50千米，工程师步行每小时行多少千米？8．小明放学后沿某路公共汽车路线以每小时4千米的速度回家，途中每隔9分钟有一辆公共汽车超过他；每隔6分钟遇见迎面开来的一辆公共汽车。

本讲主要学习三大图形处理方法： 1．理解掌握图形的分割； 2．理解掌握图形的拼合； 3．理解图形的剪拼．本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．把一个几何图形按某种要求分成几个图形，就叫做图形的分割．反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合． 将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼． 我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．板块一 图形的分割【例 1】 用一条线段把一个长方形平均分割成两块，一共有多少种不同的分割法？BAO【巩固】画一条直线，将六边形分成大小相等、形状相同的两部分，这样的直线有 条．【例 2】 把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法． 例题精讲图形的分割与拼接【巩固】把任意一个三角形分成面积相等的2个小三角形，有许多种分法．请你画出3种不同的分法．【例 3】 怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形．【例 4】 下图是一个直角梯形，请你画一条线段，把它分成两个形状相同并且面积相等的四边形．321DCBA【例 5】 在一块长方形的地里有一正方形的水池(如下图)．试画一条直线把除开水池外的这块地平分成两块．【例 6】 把下图四等分，要求剪成的每个小图形形状、大小都一样．除了剪正方形外，你还有别的方法吗？20604020【例 7】 下图是一个34 的方格纸，请用四种不同的方法将它分割成完全相同的两部分，但要保持每个小方格的完整．【巩固】右图是一个44的方格纸，请用六种不同的方法将它分割成完全相同的两部分，但要保持每个小方格的完整．【例8】下图是一个被挖去了为总面积四分之一小正方形的大正方形，请你将它分成大小形状完全一样的四部分．【巩固】下图是一个被挖去了为总面积四分之一小正方形的大正方形，请你将它分成大小形状完全一样的两部分．如果分三部分呢？【巩固】图中是由三个正三角形组成的梯形．你能把它分割成4个形状相同、面积相等的梯形吗？【例9】下图是由五个正方形组成的图形．把它分成形状、大小都相同的四个图形，应怎样分？【例10】已知左下图是由同样大小的5个正方形组成的．试将图形分割成4块形状、大小都一样的图形．【巩固】把右图剪成形状、大小相等的8个小图形，怎么剪？作出分出的小图形．【例 11】 下图是由18个小正方形组成的图形，请你把它分成6个完全相同的图形．【例 12】 一个正三角形形状的土地上有四棵大树(如下图所示)，现要把这块正三角形的土地分成和它形状相同的四小块，并且要求每块地中都要有一棵大树．应怎样分？【例 13】 将下图分割成大小、形状相同的三块，使每一小块中都含有一个○．【例 14】 请把下面这个长方形沿方格线剪成形状、大小都相同的4块，使每一块内都含有“奥数读本”这四个字中的一个，该怎么剪？本读数奥【例 15】 (2008年第八届“春蕾杯”小学数学邀请赛初赛)请把下面的图形分成形状、大小都相同的4块，使每一块里面都有“春蕾杯赛”4个字．春春蕾杯赛春春蕾蕾蕾杯杯杯赛赛赛第13题【例 16】 学习与思考对小学生的发展是很重要的，学习改变命运，思考成就未来，请你将下图分成形状和大小都相同的四个图形，并且使其中每个图形都含有“学习思考”这四个字．应怎样分？学习思考学习思考学习思考考思习学【例 17】 如下图所示，请将这个正方形分切成两块，使得两块的形状、大小都相同，并且每一块都含有学而思奥数五个字．学而思奥数数奥思而学【巩固】如下图所示的正方形是由36个小正方格组成的．如图那样放着4颗黑子，4颗白子，现在要把它切割成形状、大小都相同的四块，并使每一块中都有一颗黑子和一颗白子．试问如何切割？【例 18】 如图，甲、乙是两个大小一样的正方形．要求把每一个正方形分成四块，两个正方形共分为八块，使每块的大小和形状都相同，而且都带一个○．甲 乙【例 19】 正三角形ABC 的面积是1平方米，将三条边分别向两端各延长一倍，连结六个端点得到一个六边形(如右图)，求六边形的面积．CBA【巩固】正方形ABCD 的面积是1平方米，将四条边分别向两端各延长一倍，连结八个端点得到一个正方形(如图)，求大正方形的面积．DCB A【巩固】正六边形ABCDEF 的面积是1平方米，将六条边分别向两端各延长一倍，交于六个点，组成如下图的图形，求这个图形的面积．【例 20】 (第九届“中环杯”小学生思维能力训练活动初赛)如图，它是由15个边长为1厘米的小正方形组成的．⑴ 请在原图中沿正方形的边线，把它划分为5个大小形状完全相同的图形，分割线用笔描粗． ⑵ 分割后每个小图形的周长是 厘米．⑶ 分割后5个小图形的周长总和与原来大图形的周长相差 厘米．第3题【例 21】 如何把下图中的三个图形分割成两个相同的部分(除了沿正方形的边进行分割外，还可沿正方形的对角线进行分割)．【例 22】 (2003年《小学生数学报》数学邀请赛)如图，将一个等边三角形分割成互相不重叠的23个较小的等边三角形(这些较小的等边三角形的大小不一定都相同)，请在图中画出分割的结果．【例23】(2005年《小学生数学报》数学邀请赛)如图，将一个正方形分割成互相不重叠的21个小正方形，这些小正方形的大小不一定相同，请画图表示．板块二图形的拼合【例24】用两块大小一样的等腰直角三角形能拼成几种常见的图形？【巩固】用3个等腰直角三角形拼图，要求边与边完全重合，能拼出几种图形？【巩固】用同样大小的四块等腰直角三角板，能否拼出一个三角形、一个正方形、一个长方形、一个梯形、一个平行四边形五种图形？若能，画出示意图．【例25】下面哪些图形自身用4次就能拼成一个正方形？【例26】用下面的3个图形，拼成右边的大正方形．【巩固】用“四连块”拼成一个正方形，按编号画入右边图中．④③②①【例 27】 有6个完全相同的，你能将它们拼成下面的形状吗？【例 28】 (保良局亚洲区城市小学数学邀请赛)三种塑料板的型号如图：(A ) (B ) (C )已有A 型板30块，要购买B 、C 两种型号板若干，拼成55 正方形10个，B 型板每块价格5元，C 型板每块价格为4元．请你考虑要各买多少块，使所花的总钱数尽可能少，那么购买B 、C 两种板要花多少元？【例 29】 试用图a 中的8个相等的直角三角形，拼成图b 中的空心正八边形和图c 中的空心正八角星．板块三图形的剪拼【例30】试将一个正方形分成相同的四块，然后用这四块分别拼成三角形、平行四边形和梯形．【例31】把两个小正方形剪开以后拼成一个大正方形．【例32】将下图分成4个形状、大小都相同的图形，然后拼成一个正方形．【例33】试将一个49的长方形分割成两个大小相等、形状相同的图形，然后拼成一个正方形．【巩固】长方形的长和宽各是9厘米和4厘米，要把它剪成大小、形状都相同的两块，并使它们拼成一个正方形．【例34】将下图分成两块，然后拼成一个正方形．【例35】将图1分成4个形状、大小都相同的图形，然后拼成一个正方形．图1图2图3【例36】小龙的妈妈在街上卖边角布料的地摊上，买回了一块形状是等腰直角三角形的绸布，想用它来做长方形的窗帘，为了不把布剪的太碎，裁剪的块数就要尽可能的少，请问小龙的妈妈应该怎样剪拼呢？【例37】试将任意一个三角形分成三块，然后拼成一个长方形．【巩固】试将任意一个矩形分成两块，然后拼成一个三角形．【巩固】试将任意一个矩形分成三块，然后拼成一个三角形．【例38】把一个正方形分成8块，再把它们拼成一个正方形和一个长方形，使这个正方形和长方形的面积相等．【例39】有一块长8米、宽3米的长方形地毯，现在要把它移到长6米、宽4米的新房间里．请找出一种剪裁方法，使剪后的各块拼合后正好能铺满房间的地面，为了使剪后的地毯尽量完整，就要使剪裁的块数尽可能地少，应怎样剪拼？【例40】如何把一个长20厘米、宽12厘米的长方形切成两块，拼成一个长16厘米、宽15厘米的新长方形．【例41】长方形长24厘米，宽15厘米．把它剪成两块，使它们拼成一个长20厘米，宽18厘米的长方形．【例42】如下图长方形的长、宽分别为120厘米、90厘米，正中央开有小长方形孔，长为80厘米，宽为10厘米，要拼成面积为100平方厘米的正方形．问如何切分，能使划分的块数最少．【例43】把下图中两个图形中的某一个分成三块，最后都拼在一起，使它们成为一个正方形．【例 44】如下图两个正方形的边长分别是a和b(a b)，将边长为a的正方形切成四块大小、形状都相同的图形，与另一个正方形拼在一起组成一个正方形．ab ba【例45】如下图所示，这是一张十字形纸片，它是由五个全等正方形组成，试沿一直线将它剪成两片，然后再沿另一直线将其中一片剪成两片，使得最后得到的三片拼成两个并列的正方形．第一讲观察法在解答数学题时，第一步是观察。

三角形的切割（一）同学们大家好！三角形的面积的计算方法大家已经知道了，今日我再告诉大家一个规律：等底等高的三角形面积相等。

这是一个特别重要的规律，在解决多边形面积的很多问题中都要用到它。

今日，我们就一同来研究应用这一规律能够解决哪些问题。

【典型例题】.阅读思虑：例1.有一个三角形花坛，想把它均匀分红两个相等的三角形，能够如何分？剖析与解答：由于“等底等高的三角形面积相等”，所以要把这个三角形花坛均匀分成两个相等的三角形，就是把这个三角形花坛分红两个等底等高的三角形就能够了。

而三角形的每条边都能够作三角形的底，所以我们只需把这三条边分别二平分，再把中点与这条边相对的极点连结起来就能够了。

例2. 将任一三角形分红面积相等的六个三角形，应怎么分？剖析与解：依据等底等高的三角形面积相等这一结论，只需把原三角形分红六个等底等高的小三角形，它们的面积就必定相等。

而要找这六个等底等高的小三角形，只需把三角形的某一边六平分，再将各分点与这边相对的极点连结起来即可。

如图（1）图（1）又由于6163223，所以，假如我们把每一个小三角形的面积当作1，即16而32能够当作是先把原三角形平分两份，再把每一份分别平分红三份。

专心爱心专心1A A AB C B C B C图（2）同理，2 3能够当作是先把原三角形平分红三份，而后再把每一份平分红两份。

即A A AB C B C B C图（3）近似于这样的分法，我们还能够画出很多，这里就不一一列举了。

这两道例题有一个共同的思路，就是想方法找出等底等高的三角形，而找这类三角形，就要几平分某一条线段。

假如两个三角形的底相等，高不相等，它们的面积有什么关系呢？假如两个三角形底的长度相等，高的长度不相等，那么它们的面积之比正好等于这两个三角形高的长度比。

相同的道理，我们还能够推出，假如两个三角形高的长度相等，底的长度不相等，那么这两个三角形的面积之比正好等于它们的底的长度比，所以我们有下边的结论：假如甲、乙两个三角形的底（高）的长度相等，那么甲、乙两个三角形的面积之比等于它们的高（底）的长度之比。

四包含与排除1 二年级一班共42名同学，其中少先队员33人。

这个班男生20人，女生中有4人不是少先队员，男生中有多少人是少先队员？2 十一中学图书馆有中外文科技和文艺书共6000 册，其中中文书4560册，文艺书3060 册，外文科技书840 册。

问：一共有多少本外文书？有多少本中文文艺书？347名学生参加了数学和语文考试，其中语文得100分的12人，数学得100分的17人，两门都没得100分的有26人。

问：两门都得100 分的有多少人？4全班有46 名同学，仅会打乒乓球的有18 人，既会打乒乓球又会打羽毛球的有7 人，既不会打乒乓球又不会打羽毛球的有6人。

问：仅会打羽毛球的有多少人？5电视台向100人调查昨天收看电视的情况，有62 人看过2 频道，34人看过8频道，11 人两个频道都看过。

问：两个频道都没看过的有多少人？6一次数学小测验只有两道题，结果全班有10人全对，第一题有25 人做对，第二题有18人做错。

问：两题都做错的有多少人？7 全班50人，不会骑自行车的有23 人，不会滑旱冰的有35人，两样都会的有4 人。

两样都不会的有多少人？8五一小学举行各年级学生画展，其中18幅不是六年级的，20幅不是五年级的。

现在知道五、六年级共展出22幅画，问：其它年级共展出多少幅画？9100 个学生只有一人没学过外语，学过英语的有39人，学过法语的有49 人，学过俄语的有41 人，学过英语也学过法语的有14 人，学过英语也学过俄语的有13 人，学过法语也学过俄语的有9 人。

问：三种语言都学过的有多少人？10某班有42人，其中26人爱打篮球，17人爱打排球，19人爱踢足球，9人既爱打篮球又爱踢足球，4人既爱打排球又爱踢足球。

没有一个人三种球都爱好，也没有一个人三种球都不爱好。

问：既爱打篮球又爱打排球的有几人？11 64个小学生都订了报纸，其中订A报的28人，订B报的41人, 订C报的20人，同时订A, B报的10人，同时订A, C报的12人，同时订B, C报的也是12人。

小学奥数几何专题--图形剪拼（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）【题文】用一条线段把一个长方形平均分割成两块，一共有多少种不同的分割法？【答案】无穷多【解析】怎样把一个图形按照规定的要求分割成若干部分呢？这就是图形的分割问题．按照规定的要求合理分割图形，是很讲究技巧的，多做这种有趣的训练，可以培养学生的创造性思维，发展空间观念，丰富想象，提高观察能力．这道题要求把长方形平均分割成两块，过长方形中心的任意一条直线都可以把长方形平均分割成两块，根据这点给出如下分法(如右图)：⑴ 做长方形的两条对角线，设交点为⑵ 过点任作一条直线，直线将长方形平均分割成两块．可见用线段平分长方形的分法是无穷多的．【题文】把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法．【答案】【解析】根据等底等高的三角形面积相等这一结论，只要把原三角形分成4个等底等高的小三角形，它们的面积必定相等．而要得到这4个等底等高的小三角形，只需把原三角形的某条边四等分，再将各分点与这边相对的顶点连接起来就行了．根据上面的分析，可得如左下图所示的三种分法．又因为，所以，如果我们把每一个小三角形的面积看做1，那么就可以视为把三角形的面积直接分成4等份，即分成4个面积为1的小三角形；而可以视为先把原三角形分成两等份，再把每一份分别分成两等份．根据前面的分析，在每次等分时，都要想办法找等底等高的三角形．根据上面的分析，又可以得到如右评卷人得分下图的另两种分法．【题文】把任意一个三角形分成面积相等的2个小三角形，有许多种分法．请你画出3种不同的分法．【答案】【解析】根据等底等高的三角形面积相等这一结论，只要把原三角形分成2个等底等高的小三角形，它们的面积必定相等．而要得到这2个等底等高的小三角形，只需找出原三角形的某条边的中点与这边相对的顶点连接起来就行了．【题文】怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形．【答案】→【解析】⑴分成8块的方法是：先取各边的中点并把它们连接起来，得到4个大小、形状相同的三角形，然后再把每一个三角形分成两部分，得到如左上图所示的图形．⑵分成9块的方法是：先把每边三等分，然后再把分点彼此连接起来，得到加上右上图所示的符合条件的图形．【题文】下图是一个直角梯形，请你画一条线段，把它分成两个形状相同并且面积相等的四边形．【答案】【解析】直角梯形的上底为1，下底为2，要分成两个相同的四边形，需要一条边可以分成1和2，边长正好为3，所以边分成两段，找到的三等分点，现在，，，，所以还要找到的中点，连接，就把梯形分成完全相同的两部分．如右上图．【题文】在一块长方形的地里有一正方形的水池(如下图)．试画一条直线把除开水池外的这块地平分成两块．【答案】 【解析】用连对角线的办法找出这块长方形地的中心O和正方形水池的中心A．过O、A画一条直线，这条直线正好能把除开水池外的这块地平分为两块(如右上图)．【题文】把下图四等分，要求剪成的每个小图形形状、大小都一样．除了剪正方形外，你还有别的方法吗？【答案】【解析】先把图形分成相等的两块，每一块中再分成相等的两份，这样就不难分成四块了，如右上图．【题文】下图是一个的方格纸，请用四种不同的方法将它分割成完全相同的两部分，但要保持每个小方格的完整．【答案】【解析】分成的两块每块有(个)小格，并且这两块要关于中心点对称，大小和形状完全一样，我们从对称线入手，介绍一种分割技巧——染色法，先选中一个小格，找它关于中心点或中心线的对称位置，标上相应的符号．当找它关于中心线的对称位置时是一种情况，关于中心点的对称位置是另一种情况。

第五讲图形的分割与拼接卷Ⅰ教学目标本章内容比较抽象，在这一讲中我们主要学习几种图形处理方法：1、理解掌握图形的分割；2、理解掌握图形的拼合；3、理解图形的剪拼；4、利用剪拼图形计算、解决问题.本章中很多类型的题目还要求同学们去动手尝试．通过本章知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．有8个相等的直角三角形，你能拼成下图中的空心正八角星吗？想挑战吗分析：把一个直角三角形的斜边与另一个直角三角形的直角边的一部分重合，但顶点均不重合，依次摆放下去，便可由这八个相等的直角三角形组成如右图所示的空心正八角星．专题精讲把一个几何图形按某种要求分成几个图形，就叫做图形的分割．反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．（一）图形的分割【例1】（★★★）把如右图这样由五个正方形组成的图形，分成四块大小、形状都相同的图形→→分析：从面积考虑，把整个图形的面积分成四份，分割后的每一部分占一份.正方形，则可把每个正方形分成四个面积相等的小正方形，每块图形应有五个这样的小正方形，如右上图所示.[前铺]如右图所示是由三个正方形组成的图形，请把它分成大小、形状都相同的四个图形？→→分析：要求把原来三个正方形分成四个大小、形状都相同的四个图形，先不考虑形状，大小相同也就是面积相等，也就是把整个图形的面积分成四份，分割后的每一部分占一份，可以考虑把每一个正方形的面积分成四份，再把三个正方形中的每一个小正方形合成要求的图形，如右上图所示.[巩固]右图是由五个正方形组成的图形．把它分成形状、大小都相同的四个图形，应怎样分?分析：如果不考虑分成的四个图形的形状，只考虑它们的面积，这就要求把原来五个正方形分成四个面积相等的图形，每个图形的面积应是1个多正方形．我们把每个正方形各分成四个面积相等的小正方形，分成的每块图形应有五个这样的小正方形．根据图形的对称性，我们很快就能得到如右上图的分法.【例2】（★★★★）怎样把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.→分析：（1）分成8块的方法是：先取各边的中点并把它们连接起来，得到4个大小、形状相同的三角形，然后再把每一个三角形分成一半，得到如左上图所示的图形.（2）分成9块的方法是：先把每边三等分，然后再把分点彼此连接起来，得到加上右上图所示的符合条件的图形.[前铺]把任意一个三角形分成面积相等的4个小三角形，有许多种分法．请你画出4种不同的分法．分析：根据等底等高的三角形面积相等这一结论，只要把原三角形分成4个等底等高的小三角形，它们的面积必定相等．而要得到这4个等底等高的小三角形，只需把原三角形的某条边四等分，再将各分点与这边相对的顶点连接起来就行了.根据上面的分析，可得如左上图所示的三种分法．又因为4＝l×4＝2×2，所以，如果我们把每一个小三角形的面积看做1，那么1×4就可以视为把三角形的面积直接分成4等份，即分成4个面积为1的小三角形；而2×2可以视为先把原三角形分成两等份，再把每一份分别分成两等份．根据前面的分析，在每次等分时，都要想办法找等底等高的三角形．根据上面的分析，又可以得到如右上图的另两种分法．【例3】（★★★★）如下图所示，请将这个正方形分切成两块，使得两块的形状、大小都相同，并且每一块都含有学而思奥数五个字.→图1 图2分析：图中有相同汉字挨在一起的情况，肯定要从它们之间切开（图1），因此，首先要在它们之间划出切分线.因为要将这个正方形切开成两块形状和大小都一样的图形，所以其中一块绕中心点旋转180°必定与另一块重合.要是把切分线也绕中心点旋转180°就可得到一些新的切分线（图2）.这就为我们解决问题提供了线索，本题的两种解法如上图所示.[拓展] 如右图所示的正方形是由36个小正方格组成的.如图那样放着4颗黑子，4颗白子，现在要把它切割成形状、大小都相同的四块，并使每一块中都有一颗黑子和一颗白子.试问如何切割？分析：首先在相同颜色的棋子之间划出切分线，以中心旋转90°、180°、270°之后，得一些新的切分线，同时考虑到每块包含有一颗黑子和一颗白子的要求，以及每一块面积应该是36÷4=9，即含有9个小正方格，先找到符合要求的一块后，让它绕中心旋转90°、180°、270°便得到其他三块，如右上图.【例4】如图，甲、乙是两个大小一样的正方形.要求把每一个正方形分成四块，两个正方形共分为八块，使每块的大小和形状都相同，而且都带一个○.分析：一个正方形分成大小和形状都相同的四块，一定是从中心点分开的，只要能找出其中符合题目要求的一块，然后再将这块绕着正方形的中心点分别旋转90°、180°、270°就可以得到另外三块.又因为这个正方形面积为36平方单位，所以分成的每一块的面积都是9平方单位.即每一块都由9个小正方格组成.另外，由于两个正方形要切分成一样大小的四块，因此可将两个正方形重叠在一起考虑.①将两个正方形重叠在一起，如右图所示，为便于区别，将其中一组的“○”改写成“×”.按要求将这重叠的正方形切分成大小、形状都相同的四块，并且每块都有一个“○”和“×”.②图中有相同符号的“○”挨在一起的从中间把它们切开，在它们中间划上截线.并将这些截线绕中心点旋转90°、180°、270°得到另外三段截线.如右图.利用它们设想出划分线.③设想分块从中心位置开始，逐步向外扩散，在里层方格中，先指定某一方格已分入到某小块中，并作上记号（斜线阴影），然后将它绕中心旋转180°后得到另一方格分入到另一小块中，也作上记号（横线阴影），如右图.对于中间一层方格和最外一层方格，设想分块时一定要紧扣条件：每一块中都要有一个“○”和一个“×”.每一块都有9个方格组成，不能断开.下图是分解了的分块过程示意图.④注意到斜线阴影部分已经有了一个“○”和一个“×”.那么左下角包含“○”的方格就不能再分到斜线阴影部分去了，而只能将右下角的方格分到斜线阴影部分.于是左上角的方格就应该分给横线阴影部分.空白部分是另外两块.右图就是最后分得的结果.（二）图形的拼合【例5】（★★★★）用6个完全一样的等腰直角三角形拼图，要求边与边完全重合．你能拼出几种图形?把它们画出来．分析：建议用等腰直角三角板，把不同的边进行重合，不要漏掉旋转重合，或者准备一些等腰直角三角形的纸片，由学生拼接后贴到黑板上，见下图[前铺]用3个等腰直角三角形拼图，要求边与边完全重合，能拼出几种图形?分析： 这种类型的题需要学生亲自操作，建议教师准备材料与学生互动。

几何面积问题除了利用常规的五大模型、各种公式求得之外，还可以用图形分割的思想来做。

我们发现，在迎春杯几何问题中，这类题目很多。

掌握好这种思想方法，可以帮助我们解决很多几何难题。

解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。

解题思想：这其实就是一种化整为零的思想，各位同学不仅要学会几何题中的这种方法，更要细细体味这种思想在解决各种问题中的妙用。

模块一、简单分割【例 1】 3个相同的正方形纸片按相同的方向叠放在一起(如图)，顶点A 和B 分别与正方形中心点重合，如果所构成图形的周长是48厘米，那么这个图形覆盖的面积是__________平方厘米.【考点】图形的分割 【难度】2星 【题型】填空 【关键词】迎春杯，中年级组，复试，4题 【解析】 将这3个正方形分割，可知这个图形的周长即为两个正方形纸片的周长之和，故正方形边长为48÷8=6（厘米），则图中每个分割得到的小正方形边长为6÷2=3（厘米），所以这个图形覆盖的面积为6×6×2+3×3×2=90（平方厘米）。

【答案】90平方厘米【例 2】 正方形ABCD 的面积是1平方米，将四条边分别向两端各延长一倍，连结八个端点得到一个正方形(如图)，求大正方形的面积．DCB A【考点】图形的分割 【难度】2星 【题型】解答 【解析】 四条边分别向两端各延长一倍，很容易可以观察出，大正方形有9个小正方形组成，所以，大正方形的面积是：199⨯=(平方米)．【答案】9平方米例题精讲知识点拨4-2-4.图形的分割【例 3】 将边长为a 的正方形各边的中点连结成第二个正方形，再将第二个正方形各边的中点连结成第三个正方形，依此规律，继续下去，得到下图那么，边长为a 的正方形面积是图中阴影部分面积的________ 倍.【考点】图形的分割 【难度】3星 【题型】填空 【关键词】希望杯，四年级，复赛，第6题，4分 【解析】 阴影部分是大正方形的0.5×0.5×0.5×0.5=116，所以正方形是阴影的16倍 【答案】16倍【例 4】 正三角形ABC 的面积是1平方米，将三条边分别向两端各延长一倍，连结六个端点得到一个六边形(如右图)，求六边形的面积．CBA【考点】图形的分割 【难度】3星 【题型】解答 【解析】 采用分割法，过A 、B 、C 分别作平行线，得到右上图，其中所有小三角形的面积都相同，所以六边形面积等于13平方米．【答案】13平方米【例 5】 正六边形ABCDEF 的面积是1平方米，将六条边分别向两端各延长一倍，交于六个点，组成如下图的图形，求这个图形的面积．FED CB A FAB CDE【考点】图形的分割 【难度】3星 【题型】解答 【解析】 采用分割法，连接正六边形的对角线，会发现，所有的三角形面积都相同，一共有12个小三角形，原来正六边形的面积是1平方米，由6个小三角形组成，所以现在的大图形的面积是：122⨯= (平方米)【答案】2平方米【例 6】 长方形ABCD 的面积是40平方厘米，E 、F 、G 、H 分别为AC 、AH 、DH 、BC 的中点。

三角形的分割（二）同学们大家好！在上一讲中，我们一起研究了“三角形的分割”的一些知识。

其中有一条很重要的知识“等底等高的三角形面积相等”。

今天我们这一讲一起来研究这些知识的应用。

【典型例题】一. 阅读思考：例1. 如图，点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点。

那么阴影部分的三角形面积的和是三角形ABC的面积的。

（十一届迎春杯决赛题）分析与解答：因为D、E、F分别为AB、BC、AC的中点，所以DE、EF、DF分别平行于AC、AB、BC，所以是等底等高的三角形，，分别是等底等高的三角形。

解：即例2. 下图中，三角形ABC的面积是12平方厘米。

并且BE=2EC，F是CD的中点。

那么阴影部分的面积是（）平方厘米。

（第十二届迎春杯训练题）分析与解答：因为的高相等，而BE=2EC，所以的面积是面积的2倍。

解：（平方厘米）（平方厘米）又因为所以（平方厘米）于是又（平方厘米）所以（平方厘米）（平方厘米）【模拟试题】（答题时间：30分钟）二. 尝试练习：1. 有一张等腰直角三角形的纸片，沿它的斜边上的高把这个三角形对折；再沿小三角形的斜边上的高把它对折；再沿更小三角形斜边上的高把它对折。

这时，得到一个直角边的长是2厘米的等腰直角三角形（如下图中阴影部分）。

那么，原来的等腰直角三角形纸片的面积是多少平方厘米？2. 如下图，已知三角形ABC面积是1平方厘米，延长AB至D，使BD=AB，延长BC 至E，使CE=2BC，延长CA至F，使AF=3AC，求三角形DEF的面积。

3. 在下图中，中，E、D、G分别是AB、BC、AD的中点，图中与等积的三角形一共有多少个？4. 在图中，的面积是52平方厘米，AC=13，是等腰直角三角形，又由面积相等，求的面积是多少？5. A是所在边上的中点，B点在边上距顶点C三分之一处，阴影部分，那么（），（）。