常用数学用表

初中数理化用表引言初中数理化用表是初中学生学习数学、物理、化学等科目中常用的参考资料。

它们将复杂的知识点和公式整理成表格形式，方便学生查阅和复习。

本文将详细介绍初中数理化用表的种类和使用方法，并探讨它们在学习中的作用。

一、初中数理化用表的种类初中数理化用表根据不同学科的特点和学习内容的不同，可以分为数学表、物理表和化学表。

1. 数学表数学表主要包括基础数学公式、常用函数图像和几何图形的特征等内容。

它们按照不同的数学概念和知识点进行分类，并提供相应的公式和图像示例，帮助学生理解和记忆数学知识。

常见的数学表包括：•三角函数表：列出了常用角度的正弦、余弦、正切等函数值，方便求解三角函数相关问题。

•常用公式表：包含了如平方差公式、勾股定理等常用数学公式，用于解决各种数学问题。

•函数图像表：展示了常见函数的图像特征，帮助学生掌握函数的性质和变化规律。

2. 物理表物理表主要包括物理定律、物理量的计算公式以及常用的物理实验数据等内容。

它们按照物理学的基本概念和理论进行分类，为学生提供了必要的物理知识和数据依据。

常见的物理表包括：•物理常数表：列出了常用的物理常数，如光速、引力常数等，方便学生在计算中使用。

•运动公式表：包含了匀速直线运动、自由落体运动等常见情况的运动公式，方便学生计算运动相关问题。

•实验数据表：汇总了常见物理实验的数据，如摆动周期、电路电阻和电流关系等，供学生参考和实验验证。

3. 化学表化学表主要包括化学元素周期表、化学反应方程式和常见物质的性质表等内容。

它们按照化学元素和化学反应进行分类，为学生提供了化学领域的基本知识和实验依据。

常见的化学表包括：•元素周期表：展示了所有已知化学元素的基本信息，如原子序数、原子量和元素符号等，帮助学生了解元素的特征和分类。

•反应方程式表：列出了常见化学反应的化学方程式和反应条件，方便学生在学习和实验中运用。

•物质性质表：记录了常见物质的性质，如颜色、熔点和沸点等，供学生探究和验证物质的性质变化。

常用勾股数表什么是勾股数？勾股数又称毕达哥拉斯数，是指满足勾股定理的三个正整数a、b和c的组合。

根据勾股定理，当a、b和c满足以下关系时，它们就是一个勾股数：a² + b² = c²其中，c为斜边的长度，而a和b为直角边的长度。

例如，3、4和5就是一个常见的勾股数，因为3² + 4² = 5²。

常见的勾股数在学习和应用数学中，我们经常会遇到一些常见的勾股数。

下面是一些常见的勾股数及其对应的直角边长度：•3、4、5•5、12、13•8、15、17•7、24、25•9、40、41这些常见的勾股数在实际生活中有广泛的应用，特别是在几何学和物理学领域。

勾股数组成规律除了上述列举的常见勾股数之外，还存在其他很多不同组合的勾股数。

通过观察这些组合可以发现一些规律。

首先，我们可以发现勾股数中的直角边长度一般为奇数和偶数的组合。

例如，3、4、5中有一个奇数（3）和一个偶数（4）。

其次，两个直角边的长度之间一般存在一定的倍数关系。

例如，3、4、5中每个数都可以乘以2得到6、8和10，也满足勾股定理。

此外，我们还可以通过一些公式来生成勾股数。

例如，欧拉公式给出了生成无穷多个勾股数的方法：a = m² - n²b = 2mnc = m² + n²其中m和n为任意正整数，并且m > n。

勾股数在实际应用中的意义勾股数在几何学和物理学等领域有着广泛的应用。

下面列举了一些使用勾股数的实际应用场景：1. 测量距离在测量距离时，常常会使用勾股定理来计算两点之间的直线距离。

根据两点坐标计算它们之间的距离时，可以利用勾股定理快速求解。

2. 建筑设计在建筑设计中，常常需要考虑角度和长度之间的关系。

勾股数可以帮助建筑师计算角度和长度之间的关系，从而保证建筑的结构稳定。

3. 电子工程在电子工程中，勾股数被广泛应用于电路设计和信号处理。

数学常用字词认读表
班级学生学号
第一组：多、少、高、矮、轻、重、对、错、左边、右边、上面、下面、前面、后面
第二组：一共、还剩、原来、现在、够不够、同样多、还差、合起来
第三组：形状、正方体、长方体、圆柱、球、粗、细第四组：分类、统计、加、减、位置、规律、横着、竖着、完整
第五组：画一画、比一比、圈一圈、数一数、填一填、连一连、算一算、摸一摸、说一说、猜一猜、
写一写
第六组：大于、小于、等于、和、差、结果
第七组：刚过、快到、时针、分针、上午、下午、中午、晚上、早上
第八组：正确、合适、至少、最多、最少、接着、每次、组成、顺数、倒数
第九组：第几、单数、双数、个位、十位、一百
第十组：单元、整理、复习、解决问题、答案、算式。

数学用表（1）特殊角三角函数值sin0=0sin30=0.5sin45=0.7071 二分之根号2sin60=0.8660 二分之根号3sin90=1cos0=1cos30=0.4 二分之根号3cos45=0.1 二分之根号2cos60=0.5cos90=0tan0=0tan30=0.9 三分之根号3tan45=1tan60=1.8 根号3tan90=无cot0=无cot30=1.8 根号3cot45=1cot60=0.9 三分之根号3cot90=0（2）0°～90°的任意角的三角函数值，查三角函数表。

（见下）（3）锐角三角函数值的变化情况（i）锐角三角函数值都是正值（ii）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii）当角度在0°≤α≤90°间变化时，0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时，tanα>0, cotα>0.“锐角三角函数”属于三角学，是《数学课程标准》中“空间与图形”领域的重要内容。

从《数学课程标准》看，中学数学把三角学内容分成两个部分，第一部分放在义务教育第三学段，第二部分放在高中阶段。

在义务教育第三学段，主要研究锐角三角函数和解直角三角形的内容，本套教科书安排了一章的内容，就是本章“锐角三角函数”。

在高中阶段的三角内容是三角学的主体部分，包括解斜三角形、三角函数、反三角函数和简单的三角方程。

无论是从内容上看，还是从思考问题的方法上看，前一部分都是后一部分的重要基础，掌握锐角三角函数的概念和解直角三角形的方法，是学习三角函数和解斜三角形的重要准备。

附：三角函数值表sin0=0,sin15=（√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=（√6-√2)/4sin180=0sin270=-1sin360=0sin1=0.0 sin2=0.0 sin3=0.0sin4=0.07441253 sin5=0.0 sin6=0.6sin7=0.12 sin8=0.139173 sin9=0.17sin10=0.173648 sin11=0. sin12=0.31sin13=0.7 sin14=0.3 sin15=0.24sin16=0.6 sin17=0.29237 sin18=0.sin19=0. sin20=0. sin21=0.7sin22=0.3415912 sin23=0.39073 sin24=0.5 sin25=0.4 sin26=0.43837 sin27=0.5sin28=0.46947 sin29=0.0 sin30=0.4sin31=0. sin32=0. sin33=0.5015027sin34=0. sin35=0.6351046 sin36=0.sin37=0. sin38=0.61566 sin39=0.sin40=0. sin41=0. sin42=0.sin43=0.6 sin44=0.04589972 sin45=0.sin46=0.03386511 sin47=0. sin48=0.sin49=0.9 sin50=0.3118978 sin51=0.sin52=0. sin53=0.00472928 sin54=0.sin55=0. sin56=0. sin57=0.sin58=0.6156426 sin59=0.2 sin60=0.sin61=0. sin62=0. sin63=0.sin64=0.6299167 sin65=0. sin66=0.sin67=0. sin68=0. sin69=0.sin70=0.07859083 sin71=0. sin72=0.sin73=0. sin74=0.96126 sin75=0.sin76=0. sin77=0. sin78=0.07338057sin79=0.3447664 sin80=0.3012208 sin81=0.05951378 sin82=0. sin83=0.1641322 sin84=0.99452sin85=0.9 sin86=0.02598242 sin87=0.sin88=0. sin89=0.sin90=1cos1=0. cos2=0. cos3=0.cos4=0.02598242 cos5=0.9 cos6=0.99452cos7=0.1641322 cos8=0. cos9=0.05951378cos10=0.3012208 cos11=0.3447664 cos12=0.07338057 cos13=0. cos14=0. cos15=0.cos16=0.96126 cos17=0. cos18=0.cos19=0. cos20=0.07859084 cos21=0.cos22=0. cos23=0. cos24=0.cos25=0. cos26=0.6299167 cos27=0.cos28=0.2858927 cos29=0. cos30=0.cos31=0.3 cos32=0.6156426 cos33=0.7945424 cos34=0. cos35=0. cos36=0.cos37=0.00472928 cos38=0. cos39=0.cos40=0.3118978 cos41=0. cos42=0.cos43=0. cos44=0.03386512 cos45=0.cos46=0.04589974 cos47=0.6 cos48=0.cos49=0. cos50=0. cos51=0.cos52=0.61566 cos53=0. cos54=0.cos55=0. cos56=0. cos57=0.cos58=0. cos59=0. cos60=0.1cos61=0.02463371 cos62=0.6 cos63=0.cos64=0.438371 cos65=0.4 cos66=0.cos67=0.39073 cos68=0. cos69=0.5cos70=0. cos71=0.325568 cos72=0.5cos73=0.7 cos74=0.6 cos75=0.24cos76=0.7 cos77=0.4 cos78=0.23cos79=0.1 cos80=0.173648 cos81=0.12cos82=0.139173 cos83=0.12 cos84=0.6cos85=0.0 cos86=0.0 cos87=0.06cos88=0.0 cos89=0.04372836cos90=0tan1=0.05 tan2=0.0 tan3=0.06tan4=0.0 tan5=0.0 tan6=0.6tan7=0.6 tan8=0.5 tan9=0.27tan10=0.97 tan11=0.8 tan12=0.tan13=0.1 tan14=0.8 tan15=0.tan16=0. tan17=0.3 tan18=0.tan19=0.7 tan20=0.4 tan21=0.tan22=0. tan23=0. tan24=0.tan25=0. tan26=0. tan27=0.tan28=0. tan29=0.1452769 tan30=0.tan31=0. tan32=0. tan33=0.tan34=0. tan35=0. tan36=0.tan37=0.2 tan38=0. tan39=0.tan40=0. tan41=0. tan42=0.tan43=0. tan44=0. tan45=0.tan46=1.07905693 tan47=1.00246826 tan48=1.tan49=1. tan50=1.259421 tan51=1.6535051tan52=1.27994 tan53=1. tan54=1.37638tan55=1. tan56=1. tan57=1.tan58=1. tan59=1. tan60=1.tan61=1. tan62=1. tan63=1.tan64=2.0579296 tan65=2.6 tan66=2.3904215tan67=2.5823753 tan68=2. tan69=2.tan70=2. tan71=2.9042 tan72=3.01752526tan73=3. tan74=3. tan75=3.tan76=4.05358455 tan77=4.4284153 tan78=4.9478456 tan79=5.5970307 tan80=5.9617707 tan81=6.4675041 tan82=7.2384207 tan83=8.7974593 tan84=9.4222587 tan85=11.276132 tan86=14.6711942 tan87=19.081tan88=28.2915515 tan89=57.0759144tan90=无取值。

数学公式表(完整版)1. 数学基础公式1.1 代数公式- 平均值公式：$\frac{{x_1 + x_2 + \cdots + x_n}}{n}$- 二次方程求解公式：$x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{2a}$ - 因式分解公式：$a^2 - b^2 = (a-b)(a+b)$1.2 几何公式- 长方形面积公式：$A = l \times w$- 圆周长公式：$C = 2\pi r$- 三角形面积公式：$A = \frac{1}{2}bh$2. 微积分公式2.1 函数与导数- 函数$f(x)$在$x=c$处的导数：$f'(c) = \lim_{{h \to 0}}\frac{{f(c+h) - f(c)}}{h}$- 求导法则：- 导数的和：$(f+g)' = f' + g'$- 导数的积：$(fg)' = f'g + fg'$- 导数的商：$\left(\frac{f}{g}\right)' = \frac{f'g - fg'}{g^2}$2.2 微分与积分- 定积分：$\int_a^b f(x) dx$- 常见定积分公式：- $\int k \, dx = kx + C$- $\int x^n \, dx = \frac{{x^{n+1}}}{n+1} + C$- $\int e^x \, dx = e^x + C$- $\int \sin x \, dx = -\cos x + C$- $\int \cos x \, dx = \sin x + C$3. 概率与统计公式3.1 概率公式- 排列公式：$P(n,r) = \frac{{n!}}{{(n-r)!}}$- 组合公式：$C(n,r) = \frac{{n!}}{{r!(n-r)!}}$- 条件概率公式：$P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}$3.2 统计公式- 平均值公式：$\bar{x} = \frac{{x_1 + x_2 + \cdots + x_n}}{n}$ - 方差公式：$Var(X) = \frac{{\sum{{(x_i - \bar{x})^2}}}}{n}$ - 标准差公式：$SD(X) = \sqrt{Var(X)}$这份完整版的数学公式表包含了数学基础、微积分和概率统计方面的常用公式，希望能对您的学习和应用有所帮助。

中学数学用表
数学和其他科学知识一样，是人类解决各种问题的手段之一，在人类发展的历
史长河中发挥着重要的作用。

从20世纪以来，尤其是近几十年，数学教育的重要
性也变得越来越突出，受到更多的重视。

因此，学习数学会遇到更多的困难。

在高中时期，数学通常就是学生学习的主要科目之一。

而在我们日常学习数学
知识中，表格作为一种帮助学生理解知识的重要工具，也早已被广泛地使用了起来。

表格，也就是结构特别清晰的表格，能够深刻地显示出本质之间的联系，尤其
是在学习各种经验性的理论或数学定理时，学习者更容易掌握数学思想的基本规则。

比如，研究实数的表格，可以显示负数与正数，小数与整数之间的关系；在学习组合数学时，有比较全面的数据表，可以清晰地显示出不同数学元素的关系；对于分段函数的研究，则有以表格形式出现的各种函数系数与相应函数图像之间的联系；等等。

可以说，表格无论在把握理论，还是在训练应用能力方面，均有很大的帮助。

正确利用表格，不仅可以让学习者对数学知识的理解更加深刻，而且可以有助于培养学生的独立思考能力和实践技能，更加全面地掌握数学知识。

数学常用公式表大全数学的常用公式11、加法交换律：两数相加交换加数的位置，和不变。

2、加法结合律：三个数相加，先把前两个数相加，或先把后两个数相加，再同第三个数相加，和不变。

3、乘法交换律：两数相乘，交换因数的位置，积不变。

4、乘法结合律：三个数相乘，先把前两个数相乘，或先把后两个数相乘，再和第三个数相乘，它们的积不变。

5、乘法分配律：两个数的和与同一个数相乘，可以把两个加数分别与这个数相乘，再把两个积相加，结果不变。

如：（2+3）×5＝2×5+3×5。

6、除法的性质：在除法里，被除数和除数同时扩大（或缩小）相同的倍数，商不变。

0 除以任何不是0 的数都得0。

7、等式：等号左右两边相等的式子叫做等式。

等式的基本性质：等式两边乘同一个数，或除以同一个不为0 的数，左右两边仍然相等。

8、方程式：含有未知数的等式叫方程式。

9、一元一次方程式：含有一个未知数，并且未知数的次数是一次的等式叫做一元一次方程式。

10、分数：把单位“1”平均分成若干份，表示这样的一份或几分的数，叫做分数。

11、分数的加减法则：同分母的分数相加减，只把分子相加减，分母不变。

异分母的分数相加减，先通分，再加减。

12、分数大小的比较：同分母的分数相比较，分子大的分数大，分子小的分数小。

异分母的分数相比较，先通分，再比较；若分子相同，分母大的分数反而小。

13、分数乘整数,用分数的分子和整数相乘的积作分子，分母不变，能约分的可以先约分再计算。

14、分数乘分数,用分子相乘的积作分子，分母相乘的积作为分母，能约分的可以先约分再计算。

15、分数除以整数（0 除外）,等于分数乘这个整数的倒数。

16、真分数：分子比分母小的分数叫做真分数。

17、假分数：分子比分母大或者相等的分数叫做假分数，假分数大于或等于1。

18、带分数：由整数和真分数合成的数叫做带分数。

19、分数的基本性质：分数的分子和分母同时乘以或除以同一个数（0 除外），分数的大小不变。

小学数学公式表1. 算术运算加法- 两个数相加得到和的运算，表示为：$a + b = c$。

减法- 两个数相减得到差的运算，表示为：$a - b = c$。

乘法- 两个数相乘得到积的运算，表示为：$a \times b = c$。

除法- 一个数除以另一个数得商的运算，表示为：$a \div b = c$。

2. 几何图形长方形- 长方形的周长（周长是指围绕图形的长度）为：$P = 2 \times (a + b)$。

- 长方形的面积（面积是指图形所包括的单位面积段数量）为：$S = a \times b$。

正方形- 正方形的周长为：$P = 4 \times a$。

- 正方形的面积为：$S = a \times a$。

三角形- 三角形的周长为：$P = a + b + c$。

- 三角形的面积为：$S = \frac{1}{2} \times b \times h$。

圆形- 圆的周长（称为圆周）为：$C = 2 \times \pi \times r$。

其中，$\pi$ 是一个常数，约等于3.。

- 圆的面积为：$S = \pi \times r \times r$。

3. 分数基本定义- 分数是指一个数除以另一个数得到的结果。

分数运算- 加法：$\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}$。

- 减法：$\frac{a}{b} - \frac{c}{d} = \frac{ad - bc}{bd}$。

- 乘法：$\frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd}$。

- 除法：$\frac{a}{b} \div \frac{c}{d} = \frac{ad}{bc}$。

- 约分：将分数化简为最简形式。

4. 小数基本定义- 小数是指有小数点的数字。

小数运算- 加法：$a + b = c$。

- 减法：$a - b = c$。

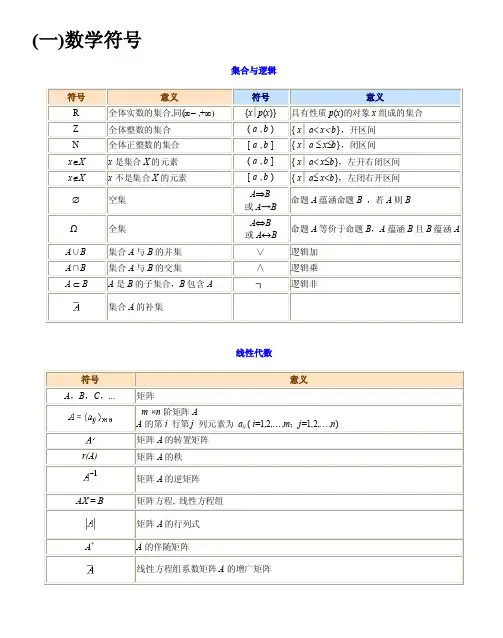
(一)数学符号集合与逻辑线性代数数列、函数与极限初等函数微积分阶导数，概率论与数理统计其它(二)高等数学常用符号大全及符号的含义示成：。

这表示<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积θvw向量v和w之间的夹角A•B×C标量三重积，以A、B、C为列的矩阵的行列式u w在向量w方向上的单位向量，即 w/|w|df 函数f的微小变化，足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数，同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数，自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。

通常f关于某变量q的偏导数为当其它几个变量固定时df 与dq的比值。

任何可能导致变量混淆的地方都应明确地表述(∂f/∂x)|r,z保持r和z不变时，f关于x的偏导数grad f 元素分别为f关于x、y、z偏导数 [(∂f/∂x), (∂f/∂y), (∂f/∂z)] 或 (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k; 的向量场，称为f的梯度∇向量算子(∂/∂x)i + (∂/∂x)j + (∂/∂x)k, 读作 "del"∇f f的梯度；它和 u w的点积为f在w方向上的方向导数∇•w向量场w的散度，为向量算子∇同向量 w的点积, 或 (∂w x /∂x) + (∂w y /∂y) + (∂w z /∂z) curl w 向量算子∇同向量 w 的叉积∇×w w的旋度，其元素为[(∂f z /∂y) - (∂f y /∂z), (∂f x /∂z) - (∂f z /∂x), (∂f y /∂x) - (∂f x /∂y)] ∇•∇拉普拉斯微分算子： (∂2/∂x2) + (∂/∂y2) + (∂/∂z2)f "(x) f关于x的二阶导数，f '(x)的导数d2f/dx2f关于x的二阶导数f(2)(x) 同样也是f关于x的二阶导数f(k)(x) f关于x的第k阶导数，f(k-1) (x)的导数T 曲线切线方向上的单位向量，如果曲线可以描述成 r(t), 则T = (dr/dt)/|dr/dt|ds 沿曲线方向距离的导数κ曲线的曲率，单位切线向量相对曲线距离的导数的值：|dT/ds|N dT/ds投影方向单位向量，垂直于TB 平面T和N的单位法向量，即曲率的平面τ曲线的扭率： |dB/ds|g 重力常数。

常用的三角函数值对照表
正弦函数（Sine Function）
正弦函数是三角函数中的一种，通常用sin表示。

在数学中，正弦函数的定义如下：
$$ \\sin(\\theta) = \\frac{对边}{斜边} $$
下表是常用角度的正弦值对照表：
角度（度）0°30°45°60°90°
正弦值00.50.7070.8661
余弦函数（Cosine Function）
余弦函数是三角函数中的一种，通常用cos表示。

在数学中，余弦函数的定义如下：
$$ \\cos(\\theta) = \\frac{邻边}{斜边} $$
下表是常用角度的余弦值对照表：
角度（度）0°30°45°60°90°
余弦值10.8660.7070.50
正切函数（Tangent Function）
正切函数是三角函数中的一种，通常用tan表示。

在数学中，正切函数的定义如下：
$$ \\tan(\\theta) = \\frac{对边}{邻边} $$
下表是常用角度的正切值对照表：
角度（度）0°30°45°60°90°
正切值00.5771 1.732∞
以上是常用的三角函数值对照表，这些数值在解决各种数学和物理问题中经常会被用到。

三角函数是数学中非常重要的概念，对于理解波动、振动、周期性等现象具有重要意义。

希望这份对照表能帮助您更好地理解和应用三角函数。

中图分类号（数学）O 数理科学和化学O1 数学O1-0 数学理论O1-6 数学参考工具书O1-64 数学表O1-641 乘法表、因数表、质数表O1-642 倒数表O1-643 乘方与开方表O1-644 对数表O1-645 三角函数表O1-646 积分表O1-647 概率论、数理统计用表O1-648 特殊函数表O1-649 计算数学用表O1-8 计算工具O11 古典数学O112 中国古典数学O113/117 各国古典数学O119 中国数学O12 初等数学O121 算术O121.1 四则O121.2 比例、百分法、利率O121.3 开方O121.4 心算法、速算法O121.5 珠算、筹算O122 初等代数O122.1 代数式O122.3 不等式O122.4 排列、组合、二项定理O122.5 极大与极小O122.6 对数、指数O122.7 级数O123 初等几何O123.1 平面几何O123.2 立体几何O123.3 几何各论O123.4 极大与极小O123.5 轨迹与几何作图O123.6 三角形与圆的几何学、近世几何学O124 三角O124.1 平面三角O124.2 球面三角O13 高等数学O14 数理逻辑、数学基础O141 数理逻辑（符号逻辑）O141.1 命题演算、谓词演算、类演算O141.12 谓词演算（命题函项演算）O141.13 类演算O141.2 证明论O141.3 递归论（递归函数、能行性理论）O141.4 模型理论O141.41 非标准分析O142 应用数理逻辑O143 数学基础O144 集合论O144.1 基本概念O144.3 公理集合论O144.4 类型论O144.5 描述集合论（解析集合论）O15 代数、数论、组合理论O151 代数方程论、线性代数O151.1 代数方程论O151.2 线性代数O151.21 矩阵论O151.22 行列式论O151.23 多线性代数O151.24 向量代数、因子代数、代数不变量论O151.25 线性不等式O151.26 线性代数的应用O152 群论O152.1 有限群论O152.2 交换群论（阿贝尔群论）O152.3 线性群论O152.4 拓扑群论O152.5 李群O152.6 群表示论O152.7 群的推广O152.8 群论的应用O153 抽象代数（近世代数）O153.1 偏序集合与格论O153.2 布尔代数O153.3 环论O153.4 域论O153.5 泛代数O154 范畴论、同调代数O154.2 同调代数O154.3 代数Ｋ-理论O155 微分代数、差分代数O156 数论O156.1 初等数论O156.2 代数数论O156.2+1 代数数域、域扩张O156.2+2 局部数域O156.2+3 分圆域O156.2+4 类域论O156.3 几何数论O156.4 解析数论O156.5 二次型（二次齐式）O156.6 超越数论O156.7 丢番图分析（丢番图数论）O157 组合数学（组合学）O157.1 组合分析O157.2 组合设计O157.3 组合几何O157.4 编码理论（代数码理论）O157.5 图论O157.6 图论的应用O158 离散数学O159 模糊数学O17 数学分析O171 分析基础O172 微积分O172.1 微分学O172.2 积分学O173 无穷级数论（级数论）O173.1 发散级数、可求和性、收敛因子O173.2 连分式论O174 函数论O174.1 实分析、实变函数O174.11 描述理论O174.12 测度论O174.13 凸函数、凸集理论O174.14 多项式理论O174.2 傅里叶分析（经典调和分析）O174.21 正交级数（傅里叶级数）O174.22 傅里叶积分（傅里叶变换）O174.23 殆周期函数O174.3 调和函数与位势论O174.4 函数构造论O174.41 逼近论O174.42 插值论O174.43 矩量问题O174.5 复分析、复变函数O174.51 单复变数函数几何理论O174.52 整数函数论、亚纯函数论（半纯函数论）O174.53 代数函数论O174.54 椭圆函数、阿贝尔函数、自守函数O174.55 拟共形映射（拟保角变换）、拟解析函数、广义解析函数O174.56 多复变数函数O174.6 特殊函数O174.61 贝赛尔函数O174.62 球面调和函数O174.63 圆柱面调和函数O174.64 椭圆面调和函数O174.66 欧拉积分O175 微分方程、积分方程O175.1 常微分方程O175.11 解析理论O175.12 定性理论O175.13 稳定性理论O175.14 非线性常微分方程O175.15 抽象空间常微分方程O175.2 偏微分方程O175.21 稳定性理论O175.22 一阶偏微分方程O175.23 二阶偏微分方程O175.24 数理方程O175.25 椭圆型方程O175.26 抛物型方程O175.27 双曲型方程O175.28 混合型方程O175.29 非线性偏微分方程O175.3 微分算子理论O175.4 高阶偏微分方程（组）O175.5 积分方程O175.6 积分微分方程O175.7 差分微分方程O175.8 边值问题O175.9 特征值及特征值函数问题O176 变分法O176.1 极小曲面方程O176.2 等周问题O176.3 大范围变分法O177 泛函分析O177.1 希尔伯特空间及其线性算子理论O177.2 巴拿赫空间及其线性算子理论O177.3 线性空间理论（向量空间）O177.3+1 拓扑线性空间O177.3+2 半序线性空间O177.3+9 其他线性空间O177.4 广义函数论O177.5 巴拿赫代数（赋范代数）、拓扑代数、抽象调和分析O177.6 积分变换及算子演算O177.7 谱理论O177.8 积分论（基于泛函分析观点的）O177.91 非线性泛函分析O177.92 泛函分析的应用O177.99 其他O178 不等式及其他O18 几何、拓扑O181 几何基础（几何学原理）O182 解析几何O182.1 平面解析几何O182.2 立体解析几何（空间解析几何）O183 向量（矢量）和张量分析O183.1 向量分析O183.2 张量分析O184 非欧几何、多维空间几何O185 射影（投影）几何、画法几何O185.1 射影（投影）几何O185.2 画法几何O186 微分几何、积分几何O186.1 微分几何O186.11 古典微分几何O186.12 黎曼几何O186.13 射影微分几何O186.14 广义空间（一般空间）O186.15 微分形式（外微分形式）O186.16 大范围微分几何O186.17 直接微分几何O186.5 积分几何O187 代数几何O187.1 代数曲线、代数曲面O187.2 簇（代数簇）O187.3 域上多胞形和其他环O189 拓扑（形势几何学）O189.1 一般拓扑O189.11 拓扑空间（空间拓扑）O189.12 维论O189.13 模糊拓扑学（不分明拓扑学）O189.2 代数拓扑O189.21 组合拓扑O189.22 同调和上同调群O189.23 同伦论O189.24 纽结理论O189.25 拓扑K-理论O189.3 解析拓扑学O189.3+1 流形的几何O189.3+2 微分拓扑O189.3+3 微分流形O189.3+4 纤维丛（纤维空间）O19 动力系统理论O192 整体分析、流形上分析、突变理论O193 微分动力系统O21 概率论与数理统计O211 概率论（几率论、或然率论）O211.1 概率基础O211.2 几何概率与组合概率O211.3 分布理论O211.4 极限理论O211.5 随机变量O211.6 随机过程O211.61 平稳过程与二阶矩过程O211.62 马尔可夫过程O211.63 随机微分方程O211.64 过程统计理论O211.65 分支过程O211.66 描述性概率O211.67 期望与预测O211.9 概率论的应用O212 数理统计O212.1 一般数理统计O212.2 抽样理论、频率分布O212.3 序贯分析O212.4 多元分析O212.5 判决函数（决策函数）O212.6 试验分析与试验设计O212.7 非参数统计O212.8 贝叶斯统计O213 应用统计数学O213.1 质量控制O213.2 可靠性理论O213.9 其他统计调整O22 运筹学O221 规划论（数学规划）O221.1 线性规划O221.2 非线性规划O221.3 动态规划O221.4 整数规划O221.5 随机规划O221.6 多目标规划O221.7 组合规划O221.8 参数规划O223 统筹方法O224 最优化的数学理论O225 对策论（博弈论）O226 排队论（随机服务系统）O227 库存论O228 更新理论O229 搜索理论O23 控制论、信息论（数学理论）O231 控制论（控制论的数学理论）O231.1 线性控制系统O231.2 非线性控制系统O231.3 随机控制系统O231.4 分布参数系统[O231.5] 复杂系统O231.9 其他O232 最优控制O233 逻辑网络理论O234 学习机理论O235 模式识别理论O236 信息论（信息论的数学理论） [O236.2] 编码理论（代数码理论）O24 计算数学O241 数值分析O241.1 误差理论{O241.2} 最小二乘法O241.3 插值法O241.4 数值积分法、数值微分法O241.5 数值逼近O241.6 线性代数的计算方法O241.7 非线性代数方程和超越方程的数值解法O241.8 微分方程、积分方程的数值解法O241.81 常微分方程的数值解法O241.82 偏微分方程的数值解法O241.83 积分方程的数值解法O241.84 差分方程的稳定性理论O241.85 共形变换（保角变换）中的计算问题O241.86 实用调和分析O242 数学模拟、近似计算O242.1 数学模拟O242.2 近似计算[O242.21] 有限元法O242.22 哈特里（Hartree）近似法O242.23 牛顿-拉弗森（Newton-Raphson）法O242.24 帕德（Pade）近似法O242.25 雷利-里茨（Rayleigh-Ritz）法O242.26 松弛法O242.27 索末菲尔德（Sommer-feld）近似法O242.28 随机近似法O242.29 区间分析法O243 图解数学、图算数学[O244] 程序设计O245 数值软件O246 数值并行计算O29 应用数学。