3.8RC低通滤波器的设计与测试

低通滤波器电路设计与实现一般来说，低通滤波器可以分为无源滤波器和有源滤波器两种。

无源滤波器是由被动元件（如电阻、电容、电感）构成的电路，直接利用被动元件的特性去除高频信号。

有源滤波器则在无源滤波器的基础上加入了主动元件（如运算放大器），增强了滤波器的性能和稳定性。

下面我们以RC无源低通滤波器为例，详细介绍低通滤波器的设计与实现。

RC无源低通滤波器是一种常见的一阶滤波器，由一个电阻R和一个电容C组成。

其基本原理是利用电容的电压延迟特性和电阻的阻性特性来实现滤波的目的。

首先，在设计RC无源低通滤波器时，首先需要确定滤波器的截止频率。

截止频率是指信号通过低通滤波器后，其幅频特性下降到-3dB时的频率。

通常情况下，截止频率可根据应用需求确定。

接下来，我们可以根据截止频率来选择合适的电容C和电阻R的数值。

根据RC滤波器的截止频率公式fc=1/(2πRC)，可以得知，电容和电阻的数值越大，截止频率越低。

因此，在选择电容和电阻时，需要根据截止频率的要求来确定。

例如，假设我们要设计一个截止频率为1kHz的RC无源低通滤波器。

为了简化计算，假设我们选择电容为1μF，求解电阻的数值。

根据截止频率公式fc=1/(2πRC)，我们可以得到R=1/(2πfc*C)。

代入数值，可得R=1/(2π*1000*1*10^-6)=159.2Ω。

因此，我们可以选择最接近该数值的标准电阻值，如160Ω。

在确定好电容和电阻的数值后，我们可以按照如下的图示，将它们组装成一个低通滤波器电路。

```---R------C---```在这个电路中，信号通过电容C后，会在电阻R上形成输出电压。

由于电容对高频信号的通过能力较差，高频成分将被滤除。

而对于低频信号，电容的阻抗相对较低，可以使其更容易通过。

因此，该电路实现了低通滤波的功能。

需要注意的是，实际电路中可能会存在元件的误差、电路的非理想性等因素，这些都可能会对滤波器的性能产生影响。

因此，在设计和实现低通滤波器时，需要对元件进行精确的选取和调试，并结合实际情况进行性能的评估和优化。

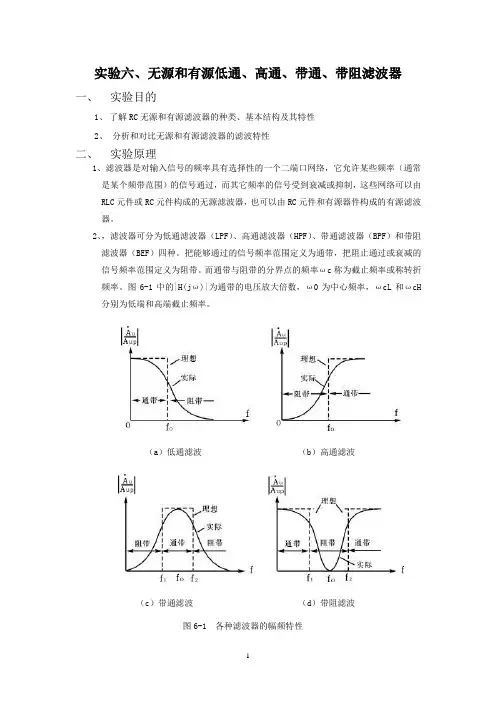
实验六、无源和有源低通、高通、带通、带阻滤波器一、实验目的1、了解RC无源和有源滤波器的种类、基本结构及其特性2、分析和对比无源和有源滤波器的滤波特性二、实验原理1、滤波器是对输入信号的频率具有选择性的一个二端口网络，它允许某些频率（通常是某个频带范围）的信号通过，而其它频率的信号受到衰减或抑制，这些网络可以由RLC元件或RC元件构成的无源滤波器，也可以由RC元件和有源器件构成的有源滤波器。

2、，滤波器可分为低通滤波器（LPF）、高通滤波器（HPF）、带通滤波器（BPF）和带阻滤波器（BEF）四种。

把能够通过的信号频率范围定义为通带，把阻止通过或衰减的信号频率范围定义为阻带。

而通带与阻带的分界点的频率ωc称为截止频率或称转折频率。

图6-1中的|H(jω)|为通带的电压放大倍数，ω0为中心频率，ωcL和ωcH 分别为低端和高端截止频率。

（a）低通滤波（b）高通滤波（c）带通滤波（d）带阻滤波图6-1 各种滤波器的幅频特性四种滤波器的实验线路如图6-2所示：(a)无源低通滤波器 (b)有源低通滤波器(c) 无源高通滤波器 (d)有源高通滤波器(e)无源带通滤波器 (f)有源带通滤波器(g)无源带阻滤波器 (h)有源带阻滤波器图6-2 几种滤波器的实验线路图3、如图6－3所示，滤波器的频率特性H （j ω），用下式来定义：式中A （j ω）为滤波器的幅频特性，θ(j ω)为滤波器的相频特性。

根据不同的滤波器，可以求出各自滤波器的H （j ω），详细的推导过程及原理，请参照《电路原理》的相关内容。

它们也都可以通过实验的方法来测量。

图6-3 滤波器三、 仪器设备1、实验主板；2、RC 滤波器模块。

四、实验内容及步骤1、滤波器的输入端接正弦信号发生器，滤波器的输出端接输出通道；2、测试无源和有源低通滤波器的幅频特性。

（1）测试RC 无源低通滤波器的幅频特性。

用图6-2（a ）所示的电路，测试RC 无源低通滤波器的特性。

低通滤波器的设计和优化低通滤波器是一种常见的信号处理器件，用于去除信号中的高频成分，保留低频信号。

在电子领域中，低通滤波器的设计和优化是一项关键任务，本文将介绍低通滤波器的基本原理、常见的实现方法以及优化技术。

一、低通滤波器的基本原理低通滤波器是一种频率选择性滤波器，它可以通过滤波器的截止频率来控制信号中通过的频率范围。

低通滤波器允许低频信号通过而抑制高频信号，常用于信号处理、音频放大、通信系统等应用中。

低通滤波器的原理基于频率响应曲线，其特点是在截止频率以下，信号的衰减较小；而在截止频率以上，则呈现出明显的衰减。

根据不同的要求和应用场景，可以选择各种类型的低通滤波器，如巴特沃斯滤波器、切比雪夫滤波器、埃尔米特滤波器等。

二、低通滤波器的实现方法低通滤波器可以通过多种方式实现，下面介绍两种常见的方法。

1. RC低通滤波器RC低通滤波器是一种简单且常见的实现方法，它基于电容和电阻的组合。

电容的特性是在高频信号下具有较大的阻抗，而在低频信号下具有较小的阻抗。

通过合理选择电容和电阻的数值，可以实现所需的截止频率。

2. 基于操作放大器的低通滤波器除了RC低通滤波器外，还可以使用操作放大器构建低通滤波器。

在这种方法中，操作放大器的反馈网络被设计为低通滤波器，以实现所需的频率响应。

根据反馈电阻和电容的数值，可以调整截止频率和滤波器的品质因子。

三、低通滤波器的优化技术为了进一步提高低通滤波器的性能，可以采用以下优化技术。

1. 选择适当的滤波器类型根据应用需求，选择适当的滤波器类型是优化低通滤波器的第一步。

不同的滤波器类型在频率响应、群延迟等方面有所差异，需根据具体情况进行选择。

2. 优化滤波器参数在设计低通滤波器时，选择合适的滤波器参数对性能具有重要影响。

例如，在RC低通滤波器中，调整电阻和电容的数值可以改变截止频率和衰减特性。

3. 级联和并联滤波器级联和并联滤波器是优化低通滤波器性能的有效方法之一。

通过将多个滤波器级联或并联，可以实现更严格的频率选择性以及更小的衰减。

RC低通滤波器设计资料讲解RC低通滤波器（Resistor-Capacitor Low-Pass Filter）是一种电子滤波器，可以通过滤除高于特定频率的信号来实现信号的平滑和去噪。

它由一个电阻和一个电容组成，通过调整电阻和电容的数值可以实现不同截止频率的滤波效果。

RC低通滤波器的工作原理是利用电容器对高频信号具有阻抗，而对低频信号具有通过性的特性。

当电容器极大时，其对高频信号的阻抗很低，几乎为空载状态。

而对于低频信号，电容器对其具有较高的阻抗，可以起到滤除高频成分的作用。

通过合理选择电阻值和电容值，可以让滤波器在特定的截止频率处起到最佳的滤波效果。

设计一个RC低通滤波器需要确定以下几个参数：1.截止频率：截止频率是指滤波器开始对信号进行衰减的频率。

一般来说，截止频率越高，滤波器对高频成分的抑制效果越好。

截止频率可以根据需要进行调整，常用的截止频率有120Hz、1kHz、10kHz等。

2.阻抗匹配：在设计RC滤波器时，需要保证信号源的输出阻抗与滤波器的输入阻抗相匹配。

这样可以防止信号源的阻抗对滤波器的传输特性产生影响。

3.选择电阻和电容：根据所需的截止频率，可以通过计算公式选择合适的电阻和电容。

其中，电容的值决定了滤波器的截止频率，而电阻的值则影响滤波器的响应时间。

较小的电阻值会导致滤波器响应更快，但也会引入更多的噪声。

4.阻带衰减：设计RC低通滤波器时应考虑阻带衰减的要求。

阻带衰减是指滤波器在截止频率之上的频率范围内，对信号的抑制程度。

较高的阻带衰减可以更好地阻止高频噪声的干扰，但也可能导致传输信号的失真。

在进行RC低通滤波器的设计之前，可以先进行一些理论计算来确定所需的电阻和电容数值。

计算公式为：截止频率f=1/(2πRC)其中，f为截止频率，R为电阻值，C为电容值。

然后，根据计算的结果选择合适的标准电阻和电容数值进行搭配。

可以使用表格或在线工具来快速找到合适的数值组合。

常见的电阻和电容值有标准数值系列，如E12、E24、E96等。

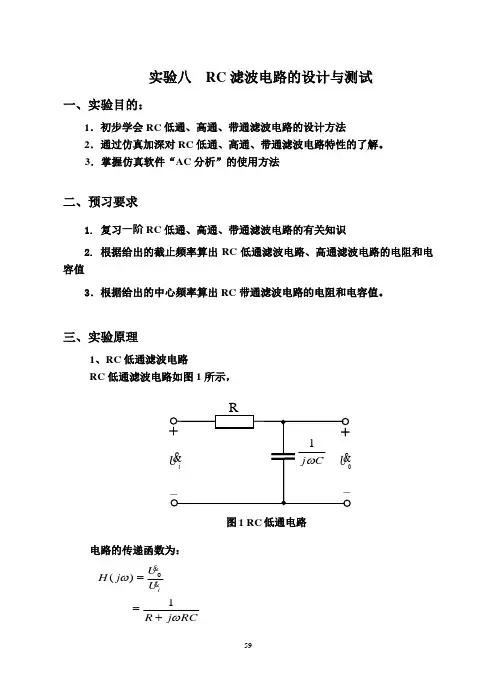
实验八 RC 滤波电路的设计与测试一、实验目的：1．初步学会RC 低通、高通、带通滤波电路的设计方法2．通过仿真加深对RC 低通、高通、带通滤波电路特性的了解。

3．掌握仿真软件“AC 分析”的使用方法二、预习要求1. 复习一阶RC 低通、高通、带通滤波电路的有关知识2. 根据给出的截止频率算出RC 低通滤波电路、高通滤波电路的电阻和电容值3．根据给出的中心频率算出RC 带通滤波电路的电阻和电容值。

三、实验原理1、RC 低通滤波电路RC 低通滤波电路如图1所示，电路的传递函数为：图1 RC 低通电路()1iU H j U R j RCωω==+幅频特性为：()H j ω=相频特性为： φ(ω)= φu0－φui ＝－arctg ωRC RC 低通滤波电路的频率特性曲线如图2所示：从幅频特性曲线可知，RC 低通滤波电路具有通低频阻高频的作用，当输入正弦信号的幅值保持不变，而频率由小到大增加时，对应频率越低的输入信号，输出电压的值越大，对应于频率越高的输入信号，输出电压的值越小，因此低频的正弦信号比高频的正弦信号更容易通过这个网络。

从相频特性曲线可知，随着ω从零向∞增加，输入信号与输入信号的相位差φ(ω)由00单调地趋向于－900。

由于φ(ω)总是负值，说明输出电压总是滞后于输入电压的，滞后的角度在00到900之间，具体数值由ω决定。

在滤波电路的幅频特性曲线中，把输出电压的幅度从最大值下降到最大值的0.707倍时所对应的角频率定义为截止角频率（临界角频率、3分贝频率），记为ωc 。

在RC 低通滤波电路的幅频特性中，角频率从0到ωc 的频率范围称为低通滤波电路的通频带，角频率大于ωc 的频率范围称为低通滤波电路的阻带。

RC 低通电路的截止角频率ωc 为：图2频率特性曲线RC （a ）幅频特性曲线 －900φ(ω－451c RCω=与ωc 对应的频率称为截止频率f c ：2、RC 高通滤波电路RC 高通滤波电路如图3所示：RC 高通滤波电路的传递函数为：其幅频特性为：相频特性为：图3 RC 高通电路()111iU H j U jRCωω==-0()901arctg CRarctgCRϕωωω=-=()H j ω=122c c f RCωππ==RC 高通滤波电路的频率特性曲线如图4所示：从图4幅频特性曲线可知，RC 高通滤波电路具有通高频阻低频的作用，当输入正弦信号的幅值保持不变，而频率由小到大增加时，对应频率越低的输入信号，输出电压的值越小，对应频率越高的输入信号，输出电压的值越大，因此频率高的正弦信号比频率低的正弦信号更容易通过这个网络。

低通滤波器设计实验报告实验报告：低通滤波器设计实验一、引言二、实验目的1.了解低通滤波器的工作原理；2.学习设计并实现一个基本的低通滤波器；3.掌握滤波器的性能指标及测试方法。

三、实验原理（插入低通滤波器的频率特性图）低通滤波器的频率特性通常由三个主要指标来描述：截止频率、通带增益和阻带抑制。

截止频率是指在该频率上，滤波器输出信号的幅度下降到输入信号幅度的一半。

通带增益是指在截止频率以下，滤波器对信号的放大倍数。

阻带抑制是指在截止频率以上，滤波器对信号的削弱。

根据实验要求，我们将设计一个RC低通滤波器。

RC低通滤波器使用一个电阻-电容（RC）电路来实现滤波功能。

其理论的3dB截止频率可由以下公式计算得出：f_c=1/(2πRC)四、实验步骤1.根据实验要求，选择合适的电阻R和电容C的数值。

推荐选择R为1kΩ，C为1uF；2.连接电阻和电容组成RC低通滤波器电路；3.输入测试信号，通过滤波器；4.测试输出信号，并记录测量值；5.使用示波器观察输入和输出信号的波形，比较滤波效果。

五、实验结果实验中我们选择了电阻值为1kΩ，电容值为1uF的RC低通滤波器进行设计。

通过实验测试，我们在输入方波信号中观察到了明显的滤波效果。

输出信号的高频分量被滤除，输出波形更加平滑。

使用示波器测量了输入和输出信号的幅度并记录如下：（插入输入输出信号的幅度测量表）根据测量结果，我们可以计算出滤波器的截止频率为：（计算结果）。

通过观察示波器上的波形，我们发现输出信号的幅度在截止频率以下保持稳定放大，而在截止频率以上则逐渐衰减。

六、实验总结通过本次实验，我们了解了低通滤波器的基本原理，并设计并实现了一个基本的RC低通滤波器。

通过观察示波器上的波形和测量输出信号的幅度，我们判断滤波器的截止频率和滤波效果。

本次实验的结果表明，RC低通滤波器可以有效滤除输入信号中的高频分量，从而实现对低频信号的保留。

滤波器的截止频率和增益等参数可以通过选择合适的电阻和电容数值来实现。

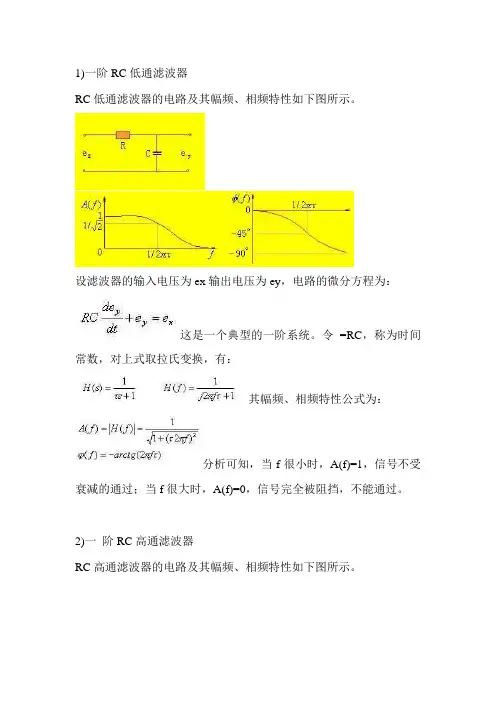
1)一阶RC低通滤波器
RC低通滤波器的电路及其幅频、相频特性如下图所示。

设滤波器的输入电压为ex输出电压为ey，电路的微分方程为：
这是一个典型的一阶系统。

令=RC，称为时间常数，对上式取拉氏变换，有：
其幅频、相频特性公式为：
分析可知，当f很小时，A(f)=1，信号不受衰减的通过；当f很大时，A(f)=0，信号完全被阻挡，不能通过。

2)一阶RC高通滤波器
RC高通滤波器的电路及其幅频、相频特性如下图所示。

设滤波器的输入电压为ex输出电压为ey，电路的微分方程为：
同理，令=RC，对上式取拉氏变换，有
或
其幅频、相频特性公式为：
分析可知，当f很小时，A(f)=0，信号完全被阻挡，不能通过；当f 很大时，A(f)=1信号不受衰减的通过.
3)RC带
通滤波器
RC带通滤波器可以看作为低通滤波器和高通滤波器的串联，其电路及其幅频、相频特性如下图所示。

其幅频、相频特性公式为：H(s) = H1(s) * H2(s)式中H1(s)为高通滤波器的传递函数，H2(s)为低通滤波器的传递函数。

有：
这时极低和极高的频率成分都完全被阻挡，不能通过；只有位于频率通带内的信号频率成分能通过。

须要注意，当高、低通两级串联时，应消除两级耦合时的相互影响，因为后一级成为前一级的“负载”，而前一级又是后一级的信号源内阻．实际上两级间常用射极输出器或者用运算放大器进行隔离．所以实际的带通滤波器常常是有源的．有源滤波器由RC调谐网络和运算放大器组成．运算放大器既可作为级间隔离作用，又可起信号幅值的放大作用．。

滤波器实验报告滤波器实验报告引言：滤波器是电子学中常用的一种设备，用于去除信号中的噪声或者选择特定频率范围的信号。

本实验旨在通过设计和实现不同类型的滤波器来研究其性能和应用。

一、低通滤波器低通滤波器是最常见的一种滤波器，其作用是通过去除高频信号，只保留低频信号。

在本实验中，我们设计了一个RC低通滤波器。

通过选择合适的电容和电阻值，我们可以调整滤波器的截止频率。

实验结果表明，当截止频率较低时，滤波器可以有效地去除高频噪声，但会对低频信号造成一定的衰减。

而当截止频率较高时，滤波器对低频信号的衰减较小，但对高频噪声的去除效果较差。

二、高通滤波器高通滤波器与低通滤波器相反，其作用是通过去除低频信号，只保留高频信号。

在本实验中，我们设计了一个RL高通滤波器。

通过选择合适的电感和电阻值，我们可以调整滤波器的截止频率。

实验结果表明，当截止频率较低时，滤波器可以有效地去除低频信号，但会对高频信号造成一定的衰减。

而当截止频率较高时，滤波器对高频信号的衰减较小，但对低频信号的去除效果较差。

三、带通滤波器带通滤波器是一种可以选择特定频率范围的信号的滤波器。

在本实验中，我们设计了一个LC带通滤波器。

通过选择合适的电感和电容值，我们可以调整滤波器的中心频率和带宽。

实验结果表明，当中心频率与信号频率相近时，滤波器可以有效地选择特定频率范围的信号。

而当中心频率与信号频率相差较大时，滤波器对信号的选择效果较差。

四、陷波滤波器陷波滤波器是一种可以去除特定频率的信号的滤波器。

在本实验中，我们设计了一个RC陷波滤波器。

通过选择合适的电容和电阻值，我们可以调整滤波器的陷波频率。

实验结果表明，当陷波频率与信号频率相近时，滤波器可以有效地去除特定频率的信号。

而当陷波频率与信号频率相差较大时，滤波器对信号的去除效果较差。

结论：通过本实验，我们深入了解了滤波器的原理、性能和应用。

不同类型的滤波器在信号处理中有着不同的作用，可以根据需要选择合适的滤波器来实现信号的处理和优化。

RC低通滤波器设计首先，让我们了解RC低通滤波器的工作原理。

RC低通滤波器由一个电阻（R）和一个电容（C）组成。

它利用RC电路的特性，通过电阻和电容之间的充放电时间常数来滤除高频噪声。

在RC低通滤波器的设计中，有几个重要的参数需要考虑。

首先是截止频率（cutoff frequency），表示滤波器开始滤除高频信号的频率。

截止频率可以通过以下公式计算：fc = 1 / (2πRC)其中，fc表示截止频率，R表示电阻值，C表示电容值。

其次是滤波器的阶数（order of the filter），表示滤波器在截止频率以上如何滤除高频信号。

阶数越高，滤波器的滤波效果越好。

常见的RC低通滤波器阶数为1和2阶。

在设计RC低通滤波器时，首先需要确定所需的截止频率和阶数。

然后，选择合适的电阻和电容值以满足设计需求。

在选择电阻值方面，一般选择较大的电阻值，以增加截止频率的精度。

电阻值的选择应考虑到电路的功耗和输入输出阻抗的要求。

在选择电容值方面，一般选择较小的电容值，以便电容器充放电的时间常数较短。

电容值的选择要考虑到滤波器的响应时间和频率范围。

此外，还应考虑电阻和电容的可用性和成本。

常见的电阻和电容值可以在电子元器件供应商的规格表中找到。

设计完RC低通滤波器后，还需要验证其性能。

可以通过使用电子设计自动化（EDA）软件进行仿真，或使用实际的电子元器件进行实验来验证滤波器的性能。

总结起来，RC低通滤波器是一种常见的电子滤波器，适用于滤除高频信号。

在设计RC低通滤波器时，需要考虑截止频率、阶数和电阻、电容值的选择。

设计完成后，可以通过仿真或实验来验证滤波器的性能。

R C低通滤波器1、电路的组成
所谓的低通滤波器就是允许低频信号通过，而将高频信号衰减的电路，RC低通滤波器电路的组成如图3-17所示。

2、电压放大倍数
令
（
（
通电路的相频特性。

在电子电路中，描述电路幅频特性和相频特性的单位通常用对数传输单位分贝。

3、对数传输单位分贝（dB）的定义
在电信号的传输过程中，为了估计线路对信号传输的有效性，经常要计算的值。

式中的P0和P i 分别为线路输出端和输入端信号的功率。

当多级线路相串联时，总的的值为：
对上式取对数可简化计算，利用对数来描述的，被定义为对数传输单位贝尔（B）。

即
（3-22）
贝尔的单位太大了，在实际上通常用贝尔的十分之一为计量单位，称为分贝（dB）。

即，1B=10dB。

（
P
（3-25）
由上式可得通带截止频率f P的物理意义是：因低通电路的增益随频率的增大而下降，当低通电路的增益下降了3dB时所对应的频率就是通带截止频率f P。

若不用增益来表示，也可以说，当电路的放大倍数下降到原来的0.707时所对应的频率。

对于低通滤波器，该频率通常又称为上限截止频率，用符号f H来表示。

根据f P的定义可得f H的表达式为：
（3-26）
（2）当f>10f P时
当f>10f P时，式3-24中的项比10大,公式中的1可忽略,式3-24的结果为
项比。