初三中考数学较难典型选择题模拟

模拟中考数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 0.33333B. πC. √4D. 1/3答案：B2. 已知函数y=2x+1，当x=3时，y的值为：A. 7B. 5C. 3D. 1答案：A3. 一个长方形的长是宽的两倍，如果宽增加2米，长减少2米，面积不变，那么原来长方形的长是：A. 4米B. 6米C. 8米D. 10米答案：B4. 一个数的平方是25，这个数是：A. 5B. -5C. 5或-5D. 以上都不是答案：C5. 以下哪个图形是轴对称图形？A. 平行四边形B. 正五边形C. 不规则多边形D. 圆答案：D6. 一个圆的半径是3厘米，那么它的周长是：A. 18.84厘米B. 9.42厘米C. 6.28厘米D. 3.14厘米答案：A7. 一个等腰三角形的底边长为6厘米，底角为45度，那么它的高是：A. 3厘米B. 4厘米C. 6厘米D. 9厘米答案：B8. 以下哪个选项是二次函数的一般形式？A. y=ax^2+bx+cB. y=ax^2+bxC. y=a(x+b)(x+c)D. y=ax+b答案：A9. 一个数的相反数是-3，那么这个数是：A. 3B. -3C. 0D. 6答案：A10. 一个数的绝对值是5，那么这个数可以是：A. 5B. -5C. 5或-5D. 以上都不是答案：C二、填空题（每题3分，共30分）11. 一个数的立方根是2，那么这个数是______。

答案：812. 一个数的倒数是1/4，那么这个数是______。

答案：413. 一个三角形的内角和是______度。

答案：18014. 一个等差数列的首项是3，公差是2，那么它的第五项是______。

答案：1115. 一个等比数列的首项是2，公比是3，那么它的第三项是______。

答案：1816. 一个直角三角形的两直角边长分别是3和4，那么它的斜边长是______。

答案：517. 一个圆的直径是10厘米，那么它的面积是______平方厘米。

一、选择题（每小题3分，共30分）1. 已知函数f(x) = ax^2 + bx + c（a≠0），若f(1) = 2，f(2) = 5，f(3) = 10，则a+b+c的值为：A. 6B. 8C. 10D. 122. 在△ABC中，角A、B、C的对边分别为a、b、c，若a=6，b=8，cosA=1/3，则△ABC的面积S为：A. 15√2B. 24√2C. 30√2D. 36√23. 已知数列{an}中，a1=1，an=an-1+√(an-1)，则数列{an}的前n项和Sn为：A. n(n+1)/2B. n(n+1)C. n(n+1)/2 + 1/2D. n(n+1)/2 - 1/24. 下列函数中，y=2x+1在y=x^2+2x+3的图象上存在反函数的是：A. y=x^2+1B. y=x^2-1C. y=x^2+2x+1D. y=x^2-2x+15. 已知正方体ABCD-A1B1C1D1的棱长为2，点E、F分别在棱AB、A1B1上，且AE=AF=√2，则异面直线EF与DD1的距离为：A. √3B. √2C. 1D. √56. 已知函数y=log2(x-1)在区间[2, +∞)上单调递增，则不等式log2(x-1) >log2(x+1)的解集为：A. (1, 3)B. (3, +∞)C. (1, +∞)D. (1, 2)7. 在平面直角坐标系中，点P的坐标为(2, -3)，点Q在直线y=-2x+1上，若PQ的最小值为√10，则点Q的坐标为：A. (1, -1)B. (2, -1)C. (3, -3)D. (4, -3)8. 已知函数f(x) = |x| - |x-2|，则函数f(x)的零点个数为：A. 1B. 2C. 3D. 49. 已知等差数列{an}的前n项和为Sn，若a1=3，S3=15，则数列{an}的公差d为：A. 2B. 3C. 4D. 510. 在等腰三角形ABC中，AB=AC，∠BAC=60°，点D在BC上，且BD=CD，则∠ADB的度数为：A. 45°B. 60°C. 90°D. 120°二、填空题（每小题4分，共40分）11. 若等比数列{an}的首项a1=1，公比q=2，则数列{an}的前n项和为______。

一、选择题（每题5分，共50分）1. 若一个等差数列的前三项分别为2，5，8，则该数列的公差是（）A. 1B. 2C. 3D. 42. 下列函数中，在定义域内是单调递增的是（）A. y = -x^2 + 4x - 3B. y = 2x - 1C. y = 1/xD. y = x^33. 在平面直角坐标系中，点A（2，3），点B（-1，4）关于直线y=x的对称点分别是（）A. A'（3，2），B'（4，-1）B. A'（3，2），B'（-1，4）C. A'（-1，4），B'（3，2）D. A'（-1，4），B'（4，-1）4. 已知三角形ABC中，∠A=60°，∠B=45°，∠C=75°，则AB：AC：BC=（）A. 1：√3：2B. √3：1：2C. 2：√3：1D. 1：2：√35. 在等腰三角形ABC中，AB=AC，AD是底边BC上的高，且AD=4cm，AB=8cm，则BC的长度是（）A. 8cmB. 12cmC. 16cmD. 10cm6. 已知函数f(x) = ax^2 + bx + c，若f(1) = 4，f(2) = 8，f(3) = 12，则a、b、c的值分别是（）A. a=2，b=0，c=2B. a=1，b=2，c=1C. a=0，b=2，c=2D. a=1，b=0，c=17. 下列数列中，是等比数列的是（）A. 1，2，4，8，16B. 1，3，9，27，81C. 1，4，16，64，256D. 1，2，4，8，16，328. 已知函数y = log2(x - 1)，则其定义域是（）A. x > 1B. x ≥ 1C. x > 0D. x ≥ 09. 在平面直角坐标系中，点P（-2，3）关于直线y=x+1的对称点Q的坐标是（）A. Q（3，-2）B. Q（-2，3）C. Q（-3，2）D. Q（2，-3）10. 若一个数的平方根是2，则这个数是（）A. 4B. -4C. 8D. -8二、填空题（每题5分，共50分）11. 已知数列{an}是等比数列，若a1=3，公比q=2，则a10=________。

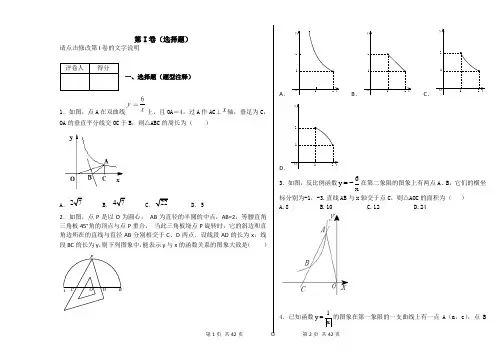
优选中考数学较难典型选择题模拟
优选中考数学较难典型选择题模拟
新世纪教育网优选资料版权全部@新世纪教育网
A．B．C．D．
7．甲、乙两同学从 A 地出发，骑自行车在同一条路上行驶到距离 A 地18km 的B 地，他
们离出发地的距离S（km）和行驶时间t(h)之间的函数关系的图象如下图.依据图中供给的
信息，切合图象描绘的说法是（）S(km) 乙甲
18
A. 甲内行驶的过程中歇息了一会
B.乙内行驶的过程中没有追上甲
O 0.5 2 2.5 t(h)
C. 乙比甲先到了 B 地
D. 甲的行驶速度比乙的行驶速度大
8、如图，正方形ABCD 边长为1，E、F、G、H 分别为各边上的点，且AE＝BF＝CG＝DH ．设
小正方形EFGH 的面积为y，AE 为x，则y 对于x 的函数图象大概是（）
y
1
o 1 x
A、B、C、D、
9．定义a b ab a b ，若3 x 27 ，则x的值是（）
A. 3
B. 4
C.6
D.9
10．如图是某一立方体的侧面睁开图，则该立方体是（）
Ａ．Ｂ．Ｃ．Ｄ．
新世纪教育网-- 中国最大型、最专业的中小学教育资源门户网站。

版权全部@新世纪教育网。

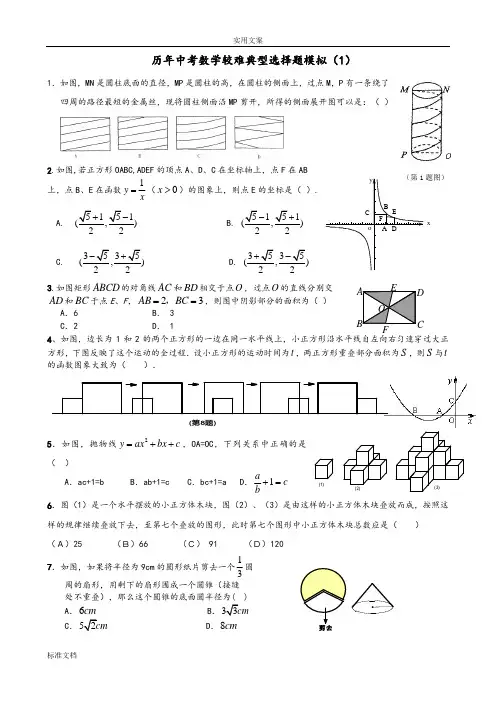
中考较难选择题模拟（6）1.汽车匀加速行驶路程为s = v （/ + ?a 尸，匀减速行驶路程为s = v （"-尸，其中v 。

、a 为常数.一汽车经过启动、匀加速行驶、匀速行驶、匀减速行驶之后停车，若把这过程中汽 车的行驶路程s 看作时间f 的函数，其图象可能是 （ ）2.已知：a>b>c,且a+b + c=O,则二次函数y = ax2+fec + c 的图象可能是下列图象中的4. 在边长为2的正方形/列中，对角线，。

与刃相交于点。

，尸是刃上一动点，过尸作研 //AC,分别交正方形的两条边于点5、F.设BAx, △舟的面积为y,则能反映）与x 之3.如图, A,B,C,D 为 。

的四等分点，动点P 从圆心。

出发，沿0-C-D-0路线作匀 设运动时间为心），匕4FB = y （。

），则下列图象中表示y 与f 之间函数关系最恰当速运动.间关系的图象为)5.一种胸花图案的制作过程如图1一图3,图1中每个圆的半径均为1.将图1绕点。

逆时针旋转60。

得到图2,再将图2绕点O逆时针旋转30°得到图3,则图3中实线的长为( )A. 71B. 2〃C. 3冗D. 4〃6.如图，点力、B、C、〃为圆。

的四等分点，动点尸从圆心。

出发，沿线段线段〃。

的路线作匀速运动.设运动时间为t秒，ZAPB的度数为y度，则下列图象中表示y与，的函数关系最恰当的是( )7.如图，直线y = -x + 4与两坐标轴分别交于虫月两点，边长为2的正方形恐F沿着x轴的正方向移动，设平移的距离为a(0<a<4),正方形恐F与△血®重叠部分的面积为S则表示S 与。

的函数关系的图象大致是( )A. B. C. D.8. 如图,BC 是 。

的直径，A 为圆上一点.点P 从点A 出发, 沿A3运动到方点，然后从方点沿BC 运动到C 点.假如点P 在整 个运动过程中保持匀速,则下面各图中，能反映点P 与点〃的距离随时间变化的图象大致是（ ）中考较难选择题模拟（6）答案 1. A 2. C3. C4. C5. D6. C7. D8. B9. A用它围成一个圆锥的A. 2 2 ——cmB. 一〃 cm 33 C. 3D. 3 ——cm —71 era 22 9.如图，扇形纸片的圆心角匕4。

初三学业模拟考试（数学）试题卷卷一（选择题）一．选择题（本题有10小题，每小题4分，共40分）1．5的相反数是 （ ） （A ）5 （B ） -5 （C ）15 （D ）15- 2．据统计，截止今年3月底，我市金融机构存款余额约为1190亿元．“1190亿元”用科学记数法可表示为 （ ）（A ）101.1910⨯元（B ）1011.910⨯元 （C ）111.1910⨯元 （D ）1111.910⨯元3．一组数据4，5，6，7，7，8的中位数是 （ ） （A ）7（B ）6.5 （C ）6 （D ）5.54．如图，在Rt △ABC 中，∠ACB =Rt ∠，BC =1，AB =2，则sin A 的值为（ ） （A（B（C（D ）125．在水平的讲台上放置圆柱形水杯和长方体形粉笔盒（如图），则它的俯视图是 ( )（A ）图① （B ）图② （C ）图③ （D ）图④6．下列等式成立的是 （ ） （A ）()313-=- （B ）()()()236222-⨯-=- （C ）22a a -= （D ）()22244x x x -=-+7．不等式235x -+>的解集是 （ ） （A ）1x >- （B ）1x <- （C ）4x >- （D ）4x < 8．把矩形ABCD 沿EF 对折后使两部分叠合，如图所示． 若115AEF ∠=︒，则∠1= （ ）（A ）50° （B ）55° （C ）60° （D ）65°9．从-1、0、1中任选一个数作为点P 的横坐标x ，再从余下的两个数中任选一个数作为点P 的纵坐标y ，那么点P （x ，y ）在函数21y x =-的图象上的概率是 （ ） （A ）13 （B ）23 （C ）16（D ）12（第5题图）图④图③图②图①（第4题图）ABC（第8题图）D10．观察下面几组数：1，3，5，7，9，11，13，15，…… 2，5，8，11，14，17，20，23，…… 7，13，19，25，31，37，43，49，……这三组数具有共同的特点。

一、选择题（每题5分，共50分）1. 已知函数f(x) = 2x^3 - 3x^2 + 4，若f(x)在x=1处的切线斜率为3，则f(x)在x=2处的切线斜率为：A. 3B. 6C. 9D. 122. 在等差数列{an}中，a1 = 2，公差d = 3，若前n项和S_n = 180，则n的值为：A. 6B. 8C. 10D. 123. 已知圆C的方程为x^2 + y^2 - 2x - 4y + 3 = 0，则圆C的半径为：A. 1B. 2C. 3D. 44. 若复数z满足|z - 1| = |z + 1|，则复数z的实部为：A. 0B. 1C. -1D. 25. 在直角坐标系中，点A(1, 2)，点B(-3, 4)，则线段AB的中点坐标为：A. (-1, 3)B. (-2, 3)C. (0, 3)D. (1, 3)6. 若a、b、c是等差数列，且a^2 + b^2 + c^2 = 3abc，则a、b、c的值可能为：A. 1, 2, 3B. 2, 3, 4C. 3, 4, 5D. 4, 5, 67. 在△ABC中，∠A = 30°，∠B = 45°，则∠C的度数为：A. 105°B. 120°C. 135°D. 150°8. 已知等比数列{an}中，a1 = 3，公比q = 2，则第n项an的值为：A. 3 2^(n-1)B. 3 2^nC. 3 2^(n+1)D. 3 2^(n-2)9. 若等差数列{an}的前n项和为S_n，公差d = 2，则S_n的表达式为：A. n^2 + nB. n^2 + 2nC. n^2 - nD. n^2 - 2n10. 已知函数f(x) = x^3 - 6x^2 + 9x - 1，若f(x)在x=2处的切线斜率为0，则f(x)在x=3处的切线斜率为：A. 0B. 3C. 6D. 9二、填空题（每题5分，共25分）11. 若函数f(x) = ax^2 + bx + c在x=1处的切线斜率为2，则a+b+c的值为______。

初三中考数学模拟试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是二次函数的图像？A. 直线B. 抛物线C. 双曲线D. 圆答案：B2. 一个圆的半径是5，那么它的面积是多少？A. 25πB. 50πC. 100πD. 25答案：B3. 计算下列哪个表达式的值等于0？A. 2x - 4 = 0B. 3x + 6 = 0C. 5x - 10 = 0D. 4x - 8 = 0答案：C4. 一个数的平方根是4，那么这个数是多少？A. 16B. -16C. 8D. -8答案：A5. 一个等腰三角形的底边长为6，高为4，那么它的周长是多少？A. 12B. 18C. 24D. 30答案：C6. 下列哪个选项是不等式的基本性质？A. 加法性质B. 乘法性质C. 除法性质D. 以上都是答案：D7. 计算下列哪个表达式的值大于0？A. 3x - 9B. 2x + 4C. 5x - 15D. 4x - 8答案：B8. 一个数的立方根是2，那么这个数是多少？A. 8B. -8C. 2D. -2答案：A9. 一个直角三角形的两条直角边长分别为3和4，那么它的斜边长是多少？A. 5B. 7C. 9D. 12答案：A10. 下列哪个选项是等式的基本性质？A. 加法性质B. 乘法性质C. 除法性质D. 以上都是答案：D二、填空题（每题4分，共20分）1. 一个数的平方等于16，那么这个数是______。

答案：±42. 如果一个数的绝对值是5，那么这个数可以是______。

答案：±53. 一个数的倒数是1/2，那么这个数是______。

答案：24. 一个数的立方是8，那么这个数是______。

答案：25. 一个等差数列的首项是2，公差是3，那么它的第五项是______。

答案：17三、解答题（每题10分，共50分）1. 解方程：2x - 5 = 9答案：x = 72. 计算：(3x - 2) / (x + 1) = 2答案：x = 13. 已知一个直角三角形的两条直角边长分别为6和8，求斜边长。

初三中考数学模拟试题及答案一、选择题（本题共10小题，每小题3分，共30分）1. 下列实数中，绝对值最小的是（）A. 2B. -3C. 0D. 1/22. 一个数的相反数是3，这个数是（）A. 3B. -3C. 0D. 13. 下列运算中，正确的是（）A. (-2)^2 = 4B. √16 = 4C. √(-4) = 2D. (-3)^3 = -274. 一个角的补角是120°，则这个角是（）A. 60°B. 30°C. 90°D. 120°5. 下列方程中，是一元二次方程的是（）A. x + 2 = 0B. x^2 + 2x + 1 = 0C. 3x - 2 = 0D. x^2 - 2xy + y^2 = 06. 在直角坐标系中，点P(-2, 3)关于x轴的对称点坐标是（）A. (-2, -3)B. (2, 3)C. (-2, 3)D. (2, -3)7. 下列不等式中，解集为x > 2的是（）A. x - 2 < 0B. x + 2 > 0C. x - 2 > 0D. x + 2 < 08. 一个三角形的两边长分别为3和5，第三边的长x满足（）A. 2 < x < 8B. 3 < x < 8C. 2 < x < 7D. 3 < x < 79. 函数y = 2x + 3的图象是（）A. 一条直线B. 一条双曲线C. 一条抛物线D. 一条曲线10. 下列统计量中，描述数据集中趋势的是（）A. 中位数B. 众数C. 方差D. 极差二、填空题（本题共5小题，每小题3分，共15分）11. 一个数的平方根是2，这个数是______。

12. 一个数的立方根是-8，这个数是______。

13. 一个角的余角是30°，则这个角是______。

14. 一个等腰三角形的底角是45°，则顶角是______。

2021中考数学较难典型选择题模拟〔4〕1.在正方体的外表上画有如图⑴中所示的粗线，图⑵是其展开图的示意图，但只在A 面上画有粗线，那么将图⑴中剩余两个面中的粗线画入图⑵中，画法正确的选项是〔 〕2．假设m 、n 〔m<n 〕是关于x 的方程1()()0x a x b ---=的两根，且a < b ， 那么a 、b 、m 、n 的大小关系是〔 〕A. m < a < b< nB. a < m < n < bC. a < m < b< nD. m < a < n < b 3．右图是一个正方体的平面展开图，这个正方体是〔 〕4．假设正方形网格中的每个小正方形的边长都是1，那么把每个小格的顶点叫做格点．现有一个外表积为12的正方体，沿着一些棱将它剪开，展成以格点为顶点的平面图形，以下四个图形中，能满足题意的是〔 〕DC B A5．将左图中的正方体纸盒沿所示的粗线．．剪开，其平面展开图的示意图为〔 〕 A ． B ． C ． D ．MMMMN'NNN'NN'NN'图2N MP纸 盒裁剪线A B C D6．将一正方体纸盒沿下右图所示的粗实线剪开，展开成平面图，其展开图的形状为〔 〕．A ． B. C. D. 7．右图是一块带有圆形空洞和矩形空洞的小木板，那么以下物体中最有可能既可以堵住圆形空洞，又可以堵住矩形空洞的是〔 〕8．如图，MN 是圆柱底面的直径，NP 是圆柱的高， 在圆柱的侧面上，点M 、P 嵌有一圈途径最短的金属丝，现将圆柱侧面沿NP 剪开，所得的侧面展开图是〔 〕纸盒剪裁线正方体纸盒9． 右图需再添上一个面，折叠后才能围成一个正方体，下面 是四位同学补画的情况〔图中阴影局部〕，其中正确的选项是〔 〕 A ． Ｂ． Ｃ． Ｄ． 10． 如图，边长为2的正方体中，一只蚂蚁从正方体下方一边AB 的中点P 出发，沿着正方体的外外表爬到其一顶点C ′ 处的最短途径是〔 〕A ．13B ．23C ．25D ．42 11. 如图，在直角梯形ABCD 中，AD ∥BC ，90C ∠=，6cm CD =，AD ＝2cm ，动点P 、Q 同时从点B 出发，点P沿BA 、AD 、DC 运动到点C 停顿，点Q 沿BC 运动到C 点停顿，两点运动时的速度都是1cm/s ，而当点P 到达点A 时，点Q 〔第11题〕 正好到达点C ．设P 点运动的时间是为(s)t ，BPQ △的面积为 y 2(cm )． 以下图中能正确表示整个运动中y 关于t 的函数关系的大致图象是〔 〕A ．B ．C ．D ．12. 如图1 ，在直角梯形ABCD 中，∠B=90°，DC ∥AB ，动点P 从B 点出发，沿梯形的边PQ ADCB由B C D A 运动，设点P 运动的路程为x ,△ABP 的面积为y , 假如关于x 的函数y 的图象如图2所示 ，那么△ABC 的面积为( ) A ．32 B ．18 C ．16D ．1013．右图是画有一条对角线的平行四边形纸片ABCD ，用此纸片可以围成一个 无上下底面的三棱柱纸筒, 那么所围成 的三棱柱纸筒可能是 〔 〕A B C D14．任何一个正整数n 都可以进展这样的分解：q p n ⨯=〔qp 、ADB (C )A (D )A (D )B (C )A (D )B (C )A (D )B (C )F EGABDCBA是正整数，且q p ≤〕，假如p q ⨯在n 的所有这种分解中两因数之差的绝对值最小，我们就称p q ⨯是n 的最正确分解，并规定：()pF n q=．例如18可以分解成118⨯、29⨯或者36⨯，这时就有31(18)62F ==．给出以下关于()F n 的说法：〔1〕1(2)2F =；〔2〕3(24)8F =；〔3〕(27)3F =；〔4〕假设n 是一个完全平方数，那么()1F n =．其中正确说法的个数是 〔 〕 Ａ．1Ｂ．2Ｃ．3Ｄ．415．，如图是一个封闭的正方形纸盒，E 是CD 中点，F 是CE 中点，一只蚂蚁从一个顶点A 爬到另一个顶点G ，那么这只蚂蚁爬行的最短道路是〔 〕A ．A —B —C —G B ．A —C —G C ．A —E —GD ．A —F —G16．如图，是一个棱长为2的正方体，一只蜘蛛在顶点A 处，一只小昆虫在顶点B 处，那么蜘蛛接近小昆虫时 所爬行的最短道路的长是 〔 〕A ．6B ．2+22C ．23．2517．如图1，是用边长为2cm 的正方形和边长为2cm 正三角形硬纸片拼成的五边形ABCDE ．在桌面上由图1起始位置将图片沿直线l 不滑行地翻滚，翻滚一周后到图2的位置. 那么由点A 到点4A 所走途径的长度为〔 〕A ．310πcm B ．()3238π+ cm C ．3212πcm D ．313πcm18．如图，每个小正方形的边长为1，把阴影局部剪下来，用剪下来的阴影局部拼成一个正方形，那么新正方形的边长是〔 〕 356参考答案 1. A 2. A 3. D 4. A 5. C 6. A 7. B 8. A 9. B 10. A 11. B 12. C13.C14.B15.C16.D17.B18.C励志赠言经典语录精选句；挥动**，放飞梦想。

初三中考数学模拟试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是二次函数的一般形式？A. y = ax^2 + bx + cB. y = ax^3 + bx^2 + cx + dC. y = ax^2 + bx + c + dD. y = ax^2 + bx + c + dx2. 已知一个直角三角形的两条直角边长分别为3和4，求斜边的长度。

A. 5B. 6C. 7D. 83. 以下哪个分数是最简分数？A. 2/4B. 3/6C. 4/8D. 5/104. 一个数的相反数是-3，那么这个数是多少？A. 3B. -3C. 0D. 65. 一个等腰三角形的底角是45度，求顶角的度数。

A. 45度B. 60度C. 90度D. 135度6. 圆的半径是5厘米，求圆的面积。

A. 25π平方厘米B. 50π平方厘米C. 75π平方厘米D. 100π平方厘米7. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 08. 以下哪个选项是不等式的基本性质？A. 如果a > b，那么a + c > b + cB. 如果a > b，那么ac > bcC. 如果a > b，那么a/c > b/cD. 如果a > b，那么a^2 > b^29. 一个长方体的长、宽、高分别是2cm、3cm、4cm，求其体积。

A. 8立方厘米B. 12立方厘米C. 24立方厘米D. 36立方厘米10. 一个多项式的最高次项系数是-1，且次数为3，这个多项式可能是？A. -x^3 + 2x^2 - 3x + 4B. -x^3 + 2x^2 + 3x - 4C. x^3 + 2x^2 - 3x + 4D. x^3 + 2x^2 + 3x - 4二、填空题（每题3分，共15分）1. 一个数的立方根是2，那么这个数是______。

2. 一个数的平方是9，那么这个数是______或______。

A BCDEFyo A BCDE FO卜人入州八九几市潮王学校2021中考数学较难典型选择题模拟〔1〕1．如图，MN 是圆柱底面的直径，MP 是圆柱的高，在圆柱的侧面上，过点M ，P 有一条绕了四周的途径最短的金属丝，现将圆柱侧面沿MP 剪开，所得的侧面展开图可以是：〔〕 2.如图,假设正方形OABC,ADEF 的顶点A 、D 、C 在坐标轴上，点F 在AB 上，点B 、E 在函数1y x=〔0x >〕的图象上，那么点E 的坐标是〔〕. A.5151(,)22+- B.5151(,)22-+ C.3535(,)22-+ D.3535(,)22+- 3.如图，矩形ABCD 的对角线AC 和BD 相交于点O ，过点O 的直线分别交AD 和BC 于点E 、F ，23AB BC ==，，那么图中阴影局部的面积为〔〕A ．6B ．3C ．2D ．14、如图，边长为1和2的两个正方形的一边在同一程度线上，小正方形沿程度线自左向右匀速穿过大正方形，以下列图反映了这个运动的全过程．设小正方形的运动时间是为t ，两正方形重叠局部面积为S ，那么S 与t 的函数图象大致为〔〕． 5．如图，抛物线2y ax bx c =++，OA=OC ，以下关系中正确的选项是〔〕A ．ac+1=bB ．ab+1=cC ．bc+1=aD ．1ac b+= 6．图〔1〕是一个程度摆放的小正方体木块，图〔2〕、〔3〕是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形，此时第七个图形中小正方体木块总数应是〔〕〔第1题图〕 (1)(2)(3)C ´CA ´〔Ａ〕25〔Ｂ〕66〔Ｃ〕91〔Ｄ〕120 7．如图，假设将半径为9cm 的圆形纸片剪去一个13圆 周的扇形，用剩下的扇形围成一个圆锥〔接缝 处不重叠〕，那么这个圆锥的底面圆半径为()A ．6cmB ．33cmC ．52cm D ．8cm8.如右图所示，是一个由白纸板拼成的立体图形， 但有两面刷上黑色，将该立体图形展开后是〔〕．9、将右图所示的硬纸片围成正方体纸盒(接缝粘贴局部忽略不计),那么围成的正方体纸盒是〔〕 10．以下四个图形中，每个小正方形都标上了颜色.假设要求一个正方体两个相对面上的颜色都一样，那么不可能是这一个正方体的展开图的是〔〕11.如图，将边长为2 cm 的正方形ABCD 沿其对角 线AC 剪开,再把△ABC 沿着AD 方向平移，得到△C B A '''ˊ，假设两个三角形重叠局部的面积是 1cm 2，那么它挪动的间隔A A 'ˊ等于〔〕A.cmB.1cmC.D.2cm 12．如图，直线b x y +=3与2-=ax y 的交点的横坐标为2-，根据图象有以下3个结论：①0>a ；②0>b；③2->x 是不等式23->+ax b x 的解集．其中正确的个数是〔〕A ．0B ．1C ．2D ．313.以下说法正确的有〔〕剪去〔第8题〕黄 红 黄红绿绿黄红 绿红 绿 黄绿 红 红绿 黄 黄 绿红黄红 黄 绿 A ．B ．C ．D ．CBAα〔1〕如图〔a 〕，可以利用刻度尺和三角板测量圆形工件的直径； 〔2〕如图〔b 〕，可以利用直角曲尺检查工件是否为半圆形； 〔3〕如图〔c 〕，两次使用丁字尺〔CD 所在直线垂直平分线段AB 〕可以找到圆形工件的圆心； 〔4〕如图〔d 〕，测倾器零刻度线和铅垂线的夹角，就是从P 点看A 点时仰角的度数．A ．1个B ．2个C ．3个D ．4个14．如图，圆锥的母线AB=6,底面半径CB=2，那么其 侧面展开图扇形的圆心角α的度数为〔〕Ａ．90oＢ．100oＣ．120oＤ．150o15．如图，在三角形纸片ABC 中，90ACB ∠=，3BC =，6AB =，在AC 上取一点E ，以BE 为折痕，使AB 的一局部与BC 重合，A 与BC 延长线上的点D 重合，那么CE 的长度为〔〕A ．3B ．6C ．23D ．316．如图1是一个小正方体的展开图，小正方体从如图2所示的位置依次翻到第1格、第2格、第3格，这时小正方体朝上面的字是〔〕 A ．京 B ．中C ．奥D ．运17.如图3，在矩形ABCD 中，AB ＝4，BC ＝3，点F 在DC 边上运动，连结AF ，过点B 作BE ⊥AF 于E ，设BE ＝y ，AF ＝x ，那么能反映y 与x 之间函数关系的大致图象是〔a 〕〔b 〕〔c 〕〔d 〕AABCDP图1 图2〔〕 ABCD 参考答案 6.C 7.A。