当前位置：文档之家 › 2414圆周角(2)

2414圆周角(2)

  • 格式：ppt
  • 大小：707.00 KB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

24.1.4圆周角(2)

24.1.4圆周角(2)
接于⊙ ， 是 上的 接于⊙O，P是AB上的 ⌒ 一点， 一点，则∠APB= 。
A P B C
例 如图⊙O1与⊙O2都经过A、B两点， 如图⊙ 两点， 经过点A的直线CD与⊙O1 交于点C，与 ⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E，与⊙O2 交于点F。 求证：CE∥DF 求证：
D A 1 C E O1 B O 2 F
C
证明： 证明： 以AB为直径作⊙O， 为直径作⊙ ， 为直径作 ∵AO=BO， CO= 1AB, ，
2
A · O B
∴AO=BO=CO. ∴点C在⊙O上. 在 上 为直径, 又∵AB为直径 为直径 ∴∠ACB=
1 ×180°= 90°. 2
为直角三角形. ∴ △ABC 为直角三角形
拓展练习
如图,点P是⊙O外一点,点A、B、Q是⊙O上 的点。（1）求证∠P＜ ∠AQB （2）如果点P在⊙O内， ∠P与∠AQB有 A 怎样的关系？为什么？
2.若ABCD为圆内接四边形，则下列 2.若ABCD为圆内接四边形， 为圆内接四边形 B ） 哪个选项可能成立（
（A）∠A∶∠ ∶∠ ∶∠ ＝ 1∶2∶3∶4 ∶∠B∶∠ ∶∠D ） ∶∠ ∶∠C∶∠ ∶ ∶ ∶ ∶∠B∶∠ ∶∠D （B）∠A∶∠ ∶∠ ∶∠ ＝ 2∶1∶3∶4 ） ∶∠ ∶∠C∶∠ ∶ ∶ ∶ ∶∠B∶∠ ∶∠D （C）∠A∶∠ ∶∠ ∶∠ ＝ 3∶2∶1∶4 ） ∶∠ ∶∠C∶∠ ∶ ∶ ∶ ∶∠B∶∠ ∶∠D （D）∠A∶∠ ∶∠ ∶∠ ＝ 4∶3∶2∶1 ） ∶∠ ∶∠C∶∠ ∶ ∶ ∶
课本 练 习
3.求证：如果三角形一边上的中线等于这边的一半，那么这个 求证：如果三角形一边上的中线等于这边的一半， 求证 三角形是直角三角形．（提示：作出以这条边为直径的圆.） ．（提示 三角形是直角三角形．（提示：作出以这条边为直径的圆 ） 1 已知： 边上的中线， 已知：△ABC 中，CO为AB边上的中线， CO= AB 为 边上的中线 且 2 求证： 为直角三角形. 求证： △ABC 为直角三角形

2414第2课时圆内角四边形的性质及圆周角定理的综合运用

2414第2课时圆内角四边形的性质及圆周角定理的综合运用

2414第2课时圆内角四边形的性质及圆周角定理的综合运用圆内角四边形的性质：圆内角四边形是指四边形的四个顶点都在同一个圆的周上的四边形。

圆内角四边形的性质有以下几点：1.任意两条对角线互相垂直：对角线是连接非相邻顶点的线段，在圆内角四边形中，任意两条对角线互相垂直。

2.互补角和补角之间的关系：圆内角四边形的互补角之和为180度，即两个互补角的和等于180度。

同时，互补角的补角也相等。

例如，如果一个角的互补角为x度，则补角也是x度。

3.一个内角等于其相对的外角：圆内角四边形的每个内角都等于其相对的外角，即两个内外角互为补角。

例如，如果一个内角为x度，则其相对的外角也是x度。

圆周角定理的综合运用：圆周角定理是指圆周角等于其所对的弧所对的圆心角的一半。

在圆内角四边形中，可以运用圆周角定理解决一些问题。

圆周角定理的表达式为：θ=β/2其中，θ表示圆周角的度数，β表示所对的圆心角的度数。

运用圆周角定理可以解决以下类型的问题：1.求解圆内角四边形的一些角的度数：通过已知条件求解圆内角四边形的一些角的度数时，可以运用圆周角定理来解决。

根据题目所给的信息，可以计算出所对的圆心角的度数，然后利用圆周角定理，计算出所需求解角的度数。

2.利用已知角的度数求解其余角的度数：当已知圆内角四边形中的一些角的度数时，可以利用圆周角定理计算出其余角的度数。

根据圆周角定理，已知角的度数乘以2即可得到所对的弧所对的圆心角的度数，然后利用互补角关系或者补角关系可以计算出其余角的度数。

3.求解圆内角四边形的对角线长度：在已知圆内角四边形的一些边长和角度的情况下，可以利用圆周角定理来求解对角线的长度。

根据题目给定的信息，可以计算出所需求解对角线所对的圆心角的度数，然后利用圆周角定理，将所对的圆心角的度数带入相应的表达式中，计算出对角线的长度。

通过综合运用圆内角四边形的性质和圆周角定理，可以解决一系列与圆内角四边形相关的问题。

理解和掌握这些性质和定理，有助于我们在解决具体问题时运用正确的方法和技巧，提高解题的效率和准确性。

20《2414圆周角2》PPT课件

20《2414圆周角2》PPT课件

C1
C2
C3Biblioteka A OB3同圆或等圆中，相等的圆周角所对的弧也 相等。
AB
））
∵ ∠CAD=∠EBF ∴ CD=EF
E O
C
F
F
D
4
课前练习：
1. 如图, △ABC是等边三角形，点D 是⊙O上一点，则∠BDC = 60°；
图3 B
A D
O C
5
2.如图，在⊙O中，AB是⊙O的 直径，∠D＝20°，则∠AOC的 度数为_1_4_0_°_
You Know, The More Powerful You Will Be
18
谢谢大家
荣幸这一路，与你同行
It'S An Honor To Walk With You All The Way
演讲人：XXXXXX
时 间：XX年XX月XX日
19
1
圆周角定理
在同圆或等圆中，同弧或等弧所对的圆
周角相等，都等于这条弧所对的圆心角的
一半．
C
老师提示:
D
圆周角定理是承
上启下的知识点,要予
以重视.
A
O ·
B
2
推论：半圆（或直径）所对的圆周角是 直角，900的圆周角所对的弦是直径。
∵ AB是直径 ∴ ∠AC1B=900
∵ ∠AC1B=900 ∴ AB是直径
∠A+∠C=_1_80°，∠B+∠ADC=_1__8_0_°;
若∠B=800，
则∠ADC=__1_0__0_°∠CDE=__8_0_°__
A D
E
80
B
C
12
(2)四边形ABCD内接于⊙O，∠AOC=1000, 则∠B=____,∠D=___5_0_°_ 130°

人教版九年级数学上册《24.1.4圆周角》教案

人教版九年级数学上册《24.1.4圆周角》教案
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与圆周角相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。这个操作将演示圆周角定理的基本原理。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“圆周角在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
此外，学生小组讨论环节，我发现大家在讨论“圆周角在实际生活中的应用”这一主题时，思路较为局限。为了拓宽学生的思维，我今后可以多提供一些与圆周角相关的实际案例，让他们在讨论时有更多的借鉴和启发。
最后，总结回顾环节，我希望通过提问的方式了解学生对课堂内容的掌握情况。但从学生的回答来看，他们对圆周角知识点的掌握还不够扎实。因此，我计划在接下来的课堂中，增加一些针对性的练习，帮助他们巩固所学知识。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了圆周角的定义、圆周角定理以及它们在实际中的应用。同时，我们也通过实践活动和小组讨论加深了对圆周角的理解。我希望大家能够掌握这些知识点，并在解决与圆相关的问题时灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解圆周角的基本概念。圆周角是由圆上两条半径或弦所夹的角。它是研究圆的重要几何性质之一，对于解决与圆相关的问题具有重要意义。

241圆-2414圆周角课件人教新课标九年级上

241圆-2414圆周角课件人教新课标九年级上

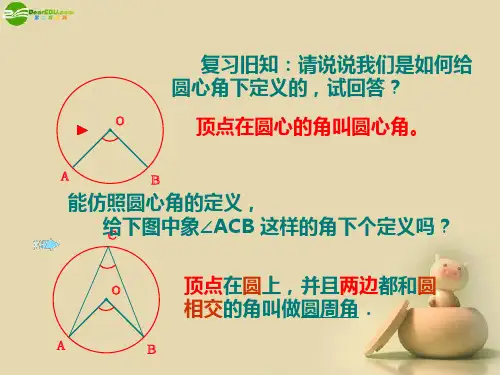
2.上节课我们学习了一个反映圆 心角、弧、弦三个量之间关系的 一个结论，这个结论是什么？ 在同圆（或等圆）中，如果圆心角、弧、弦有 一组量相等，那么它们所对应的其余两个量都 分别相等。

一.复习引入: 答:顶点在圆心的角叫圆心角 1.圆心角的定义?一、概念什么叫做I【周角?顶点在圆上，并且两边都和圆相交的角.DE B辩一辩图中的Z CDE是圆周C D练习一：判断下列各图中，哪些是圆周角，为什么?如图是一个圆柱形的海洋馆的横截面的示意图，人们可以 通过其中的圆弧形玻璃血 观看窗内的海洋动物，同学甲站 在圆心的0位置，同学乙站在正对着玻璃窗的靠墙的位置 C,他们的视角 2A0B 和Z 应劫 有什么关系？如果同学 丙、丁分别站在他靠墙的位置踊他们的视角（ZADB 和Z 血）和同学乙的视角相同吗？丙PZAOB 是AB 所对的圆心角IT v= A丁EZACB是AB所对的圆周角Z ADB是AB所对的圆周角ZAEB是AB所对的圆周角它们之间有什么关系呢?中，同弧或等弧所对的圆心角相等. 中，同弧或等弧所对的 为了解决这个问题，我们先探究同弧所对的圆周角 和圆心角之间有的关系.你会画同弧所对的圆周 角和圆心角吗?■在同 或等■在同 或角有什么关系？教师提不:注意圆心与圆周角的位置关系•(1)折痕是I角的一条边,(2)折痕在I角的内部,(3)折痕在圆周角的外部.C c C图23.1.11■如图，观察圆周角ZABC与圆心角ZAOC,它们的大小有什么关系?■说说你的想法，并与同伴交流・A AC分别量一下图中所对的两个角的度数，比较一下，再变动点6®圆周上的位置，圆周角的度数有没有变化？你能发现什么规律吗?再分别量出图中所对的加冋角和圆心角的度数，比较一下, 角・gsp你什么发现?同弧所对的圆周角的度数没有变化，并且它的度数恰好等于这条弧所对的圆心角的度数的一半.1•如图，点人B、G刀在同一个圆上，四边形如?的对角线把4个内角分成8个角，这些角中哪些是相等的角？Z1 = Z4 Z5= Z8 Z2= Z7 Z3= Z6c A87236同弧所对角与圆心角的关系■当圆心(0)在圆周角(NABC)的一边(BC)±时, NABC与圆心角ZA0C的大小关系.•••NA0C 是ZkABO 的外角,AZA0C=ZB+ZA.B/OA=OB,AZA=ZB.AZA0C=2ZB. 即ZABC= 2A OC.你能写出这个命题吗?同弧所对的圆周角等于它所对的圆心角的一半.目千怖对圆周角与圆心角的关系■如果圆心不在圆周角的一边上，结果 会怎样？■ 2.当圆心(0)在因冋 时,圆周角2ABC 与0 小关系会怎样？老师提示:能否转化为1的情况? 过点B 作直径BD ■由1可得：同弧所对的圆周角等于它所对ZABD = *A0D, ZCBD =女COD,21・•・上ABC =羊AOC.你能写出这个命题吗？的圆心角的一半・/迅0)在圆周角(ZABC)的外 甥野与圆心角羽的老师提示:能否也转化为1的情况? 过点B 作直径BD •由1可得：NABD = ZAOD, ZCBD =|ZCOD,1・•・ ZABC =孑 AOC.你能写出这个命题吗？■如果圆心不在 会怎样？ ■ 3. 部C3同弧所对的圆周角等于它所对 的的_半・］周cc■综上所述, 周角NABC与心角NAOC的大小关系是■同弧所对的圆周角等于它所对的圆心角的一半.即NABC =学AOC.矗®所谕，ZADB、ZACB、ZAOB今樹是件么角？它们韦何昙同止7 ZADB与ZACB韦什么矣*7圆周角定理:C11严同弧（等弧）所对的囱冋角相等.D0A都等于这条弧所对的圆心角的一半.思考：在同圆或等圆中相等的圆周角所对的弧相等 B 吗？111°111在同圆或等圆中相等的I角所对的弧相等.如图，若AC = BD 则Z D= ZA・・・AB〃CD■ 1 •如图，在。

《2414圆周角2》PPT课件

《2414圆周角2》PPT课件
6
3.如图，AB和CD都是⊙0的直径， ∠AOC=60°，则∠C的度数
是 30° 。
C AO B
D
7
4、如图，AB是⊙O的直径，
点C在圆上,∠A=20°,则
∠B= 70 度
C
Ａ Ｏ
B
8
新课讲解：
若一个多边形各顶点都在同一 个圆上，那么，这个多边形叫做 圆内接多边形，这个圆叫做这个 多边形的外接圆。
∠A+∠C=_1_80°，∠B+∠ADC=_1__8_0_°;
若∠B=800，
则∠ADC=__1_0__0_°∠CDE=__8_0_°__
A D
E
80
B
C
12
(2)四边形ABCD内接于⊙O，∠AOC=100
A
100 D
O
B
C
13
(3)四边形ABCD内接于⊙O, ∠A:∠C4=51°:3,则∠13A5=°_____,∠C=_____,
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
19
D E
B
C
C
O
A B
A
O
D
F
E
9
如图
四边形ABCD为⊙O的
D
内接四边形；
A O
⊙O为四边形ABCD
的 外接圆。
B
C
10
如图：圆内接四边形ABCD中，
∵ 弧BCD和弧BAD所对的
圆心角的和是周角
D
∴∠A＋∠C＝180°A

新人教版九年级数学上册《24.1.4圆周角(2)》公开课课件

新人教版九年级数学上册《24.1.4圆周角(2)》公开课课件
2020年2月28日星期五
作业:
A层（基础题）
练习册第102--104页第 1--3 题、 第 1--2 题、 第 1--4 题．
B层（拓展题）
练习册第103--104页第 3题、第 5--7 题．
2020年2月28日星期五
选做作业
（1）如下图左，四边形 ABCD 内接于⊙O，AB 是 直径，∠ABD =30°，则∠BCD 的度数为多少？
（2）如下图右，在⊙O 中，AB 为直径，直线 l 与 ⊙O 交于点 C、D，BE⊥l 于点 E，连接 BD、BC．
求证：∠CBE =∠ABD． z.xx.k
D C
A
O
B
A
O
B
D
CE lห้องสมุดไป่ตู้
2020年2月28日星期五
D
与 ∠A的数量关系？ A
∠DCE＋∠∠1A与＝∠18D0C°E
又 ∠A ＋∠为1＝内对18角0°
所以∠A＝∠DCE
O
1
E
B
C
2020年2月28日星期五
3．性质推导
几何表达式： ∵ ABCD是⊙O
A
D 1E
的内接四边形， z.xx.k
∴ ∠A+∠C=180°
O
且∠B=∠1 B
C
2020年2月28日星期五
C
⊙O为四边形ABCD的外接圆。
2020年2月28日星期五
2．性质探究
观察圆内接四边形对角之间有什么关系． 如何验证你的猜想呢？
A DE
O
F
B
C
圆内接四边形的对角互补，并且任何一角的外角都 等于它的内对角．
2020年2月28日星期五
2．性质探究

2414圆周角定理及其运用课件新人教版

2414圆周角定理及其运用课件新人教版

C
6
A
O
B
P 10
D
练习:如图 AB是⊙O的直径, C ,D是圆上的两 点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.
D
A
O 40° B
C
例2 在足球比赛场上，甲、乙两名队员互相配合向对方球门MN 进攻，当甲带球冲到A点时，乙已跟随冲到B点(如图2)．此时甲是 自己直接射门好，还是迅速将球回传给乙，让乙射门好？
∠MAN＜∠MCN，而∠MCN=∠MBN， 所以∠MAN＜∠MBN． 因此，甲应将球回传给乙，让乙射门.
如图所示，已知⊿ABC的三个顶点都在⊙O 上，AD是⊿ABC的高，AE是⊙O的直径. 求证：∠BAE＝∠CAD
A
B E
O DC
探究
3、如图，AB是⊙O的直径，BD是⊙O的弦，延长 BD到点C，使DC=BD，连接AC交⊙O于点F，点 F不与点A重合。
A
E B
C D
E
A⌒C所对的圆周角∠ AEC ∠ ABC
●O
∠ ADC的大小有什么关系？
C
B
规律：都相等，都等于圆心角∠AOC的一半
D
结论：在同圆或等圆中，同弧或等弧所
对的圆周角相等。
巩固练习：
如图，点A,B,C,D在同一个圆上，四 边形ABCD的对角线把4个内角分成 8个角，这些角中哪些是相等的角？
拓展练习
如图,点P是⊙O外一点,点A、B、Q是⊙O上的 点。（1）求证∠P＜ ∠AQB
（2）如果点P在⊙O内， ∠P与∠AQB有怎样的
关系？为什么？
A
Qp O
B
=
1∠AOD,
2
∠CBD
=1
2
∠COD,

人教版九年级上册 24.1.4 圆周角 课件30张

人教版九年级上册 24.1.4 圆周角 课件30张

五、思维拓展
与圆有关的角除了圆心角、圆周角还有其 它的角，比较∠A、∠D、∠E的大小关系，你 有什么发现？能说明你的结论吗？
D’
A
E’ E
D
B
C
练习. 如图，在⊙O中，BC=2DE,∠BOC=84°，求
∠A的度数.
C E
A
O
D
B
活动六：反思提升
目标检测
1.如左图，OA、OB、OC都是⊙O的半径，
24.1.4圆周角
一、温故探新 定义 顶点在圆心的角叫做圆心角.
O
B
C
二、建立概念
圆周角
类 比 思
定义 顶点在圆上， 并且两边都和圆相交 的角叫做圆周角.
想
圆心角
B C
· · B 定义O 顶点A 在圆心 O
A
的角叫做圆心角.
C
（1）√
（2） ×
A O
B
C
A C
·O
B
（3）×
圆周角
定义 顶点在圆上， 并且两边都和圆相交 的角叫做圆周角.
四边形ABCD的对角线.填空：
(1)∠1=∠ 4 ; (2)∠2=∠ 7 ; (3)∠3=∠ 6 ; (4)∠5=∠ 8 .
1.如图，点A、B、C都在⊙O上. （1）若∠AOC=120°，则求∠ABC的度数. （2）写出∠AOC与∠ABC的数量关系.
O
C
A
B
2.如图，点A、B、C都在⊙O上. ∠AOB = 2∠BOC. 请说明∠ACB = 2∠BAC.
O
C
A
B
一、温故探新 定义 顶点在圆心的角叫做圆心角. 性质 弧的度数等于它所对圆心角的度数.
O
B

人教版九年级上册数学教学课件 第24章 圆24.1.4 圆周角(第2课时)

人教版九年级上册数学教学课件 第24章 圆24.1.4 圆周角(第2课时)
∴∠BCD=180°-∠A=111°， ∴∠DCE=180°-∠BCD=69°．故选A．
3.已知如图，在圆内接四边形ABCD中， ∠B=30°，则∠D=__1_5_0_．°
解析:∵圆内接四边形ABCD中，∠B=30°， ∴∠D=180°-30°=150°．故填150°．
4.如图，四边形ABCD内接于⊙O，AB是⊙O的直径， ∠BCD=120°，BC=CD． (1)求证：CD∥AB； (2)求S△ACD：S△ABC的值． 解：（1）∵AB是⊙O的直径，∴∠ACB=90°， ∵∠BCD=120°， ∴∠ACD=30°，∠DAB=180°-∠BCD=60°， ∵BC=CD，∴弧BC=弧CD， ∴∠DAC=∠BAC= 1 ×60°=30°，
学生课堂行为规范的内容是： 按时上课，不得无故缺课、迟到、早退。 遵守课堂礼仪，与老师问候。 上课时衣着要整洁，不得穿无袖背心、吊带上衣、超短裙、 拖鞋等进入教室。 尊敬老师，服从任课老师管理。 不做与课堂教学无关的事，保持课堂良好纪律秩序。
谢 谢 大 家 听课时有问题，应先举手，经教师同意后，起立提问。
证明：如图所示，连接OB，OD. ∵∠A所对的弧为 BCD ,
∠C所对的弧为 BAD ,
又∵ BCD 和 BAD 所对的圆心角的和是周角，
∴∠A+∠C= 3600 =180°.
2
同理∠B+∠D=180°.
C
B 圆内接四边形的
性质：圆内接四 边形的对角互补.
D
A
1.圆内接四边形的外角等于它的内对角.
上课期间离开教室须经老师允许后方可离开。 上课必须按座位表就坐。 要爱护公共财物，不得在课桌、门窗、墙壁上涂写、刻划。 要注意保持教室环境卫生。 离开教室要整理好桌椅，并协助老师关好门窗、关闭电源。

24.1.4 圆周角(2)--

24.1.4 圆周角(2)--
则BC= 5cm
O ● C
B
3.如图,△ABC的顶点均在⊙O上, AB=4, ∠C=30°,求⊙O的直径.
AE=2AB=8
A B
O ●
C
E
1.如图,AB是⊙O的直径，BD是弦, 延长BD到C,使DC=BD,AC与AB的 大小有什么关系?为什么?
A
O ●
C DB
2.如图⊙O中,D、E分别是A⌒B和A⌒C的中
· O
B
∴AO=BO=CO. ∴点C在⊙O上.
又∵AB为直径, ∴∠ACB=0.5×180º= 90°.
∴ △ABC 为直角三角形.
概念
如果一个多边形的所有顶点 都在同一个圆上，这个多边形叫 做圆内接多边形，这个圆叫做这 个多边形的外接圆. D
A
O
C
B
判断命题的真假：
在同圆或等圆中，同弦或等弦所 对的圆周角相等.
点, DE分别交AB和AC于点M、N; 求证:△AMN是等腰三角形.
A
D MN
E
O ●
B C
3, 如 图 所 示 ， AB ， AC 是 ⊙ O 的 弦 ， AD⊥BC于D，交⊙O于F，AE与⊙O的 直径，试问两弦BE与CF的大小有何关 系，说明理由．
21 3
） ）
知识深化
如图，以⊙O的半径OA为直径作⊙O1,
∴OA=OB=AB=2，即半径为2.
例题讲解 例.如图⊙o的直径AB为
10cm,弦AC为6cm, ∠ACB的平分线交
⊙o于点D,求BC,AD,BD的长.
解：∵AB是直径，
C
∴ ∠ACB= ∠ADB=90°．
8
BC = AB2 - AC2 = 102 - 62 = 8
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

方法三
方法一
O
A
B
C
O
方法二
A D
·
B
方法四
O
课堂Байду номын сангаас结:
（1）本节课主要学习了哪些内容？ （2）本节课学到了哪些思想方法？
① 构造圆内接四边形； ② 一题多解，一题多变．
11、四边形ABCD内接于⊙O,BA、 CD的延长线交于P,AD=２ cm,BC=３cm,ＰＡ＝４cm，求ＰＣ 的长.
12.已知：如图，四边形ABCD 是圆的内接四边形并且ABCD 是平行四边形。
求证：四边形ABCD是矩形。
A
B
O
D
C
拓展：
如图，你能设法确定一个圆形纸片的圆心吗？你有多少
种方法？与同学交流一下．
24.1.4 圆周角（2）
回顾：圆周角定理及推论？ 思考：判断正误： 1.同弧或等弧所对的圆周角相等（√ ） 2.相等的圆周角所对的弧相等（× ） 3.90°角所对的弦是直径（√ ） 4.直径所对的角等于90°（ × ） 5.长等于半径的弦所对的圆周角等于30°（√ ）
新课讲解：
若一个多边形各顶点都在同一
5.四边形ABCD内接于⊙O，则 ∠A+∠C=__18_0_°__ ∠B+∠ADC=__1_8_0_°__;若
∠B=80°，则∠ADC=_1_0_0_°∠CDE=__8_0_°__
A
A
D
E
D
80
B
C
O
B
C
6.四边形ABCD内接于⊙O，∠AOC=100° 则∠B=_5_0_°___∠D=__1_3_0_°_
B
B
DD
OO
CC
圆内接四边形的对角互补。
如果延长BC到E，那么 ∠DCE＋∠BCD ＝180°
又 ∠A ＋∠BCD＝ 180°
所以∠A＝∠DCE
D
A
O
B
E C
练习：
1、如图，四边形ABCD内接于⊙O,如果
∠BOD=130°,则∠BCD的度数是（ ）
A
A、115° B、130° O
C、65° D、50° B
7.四边形ABCD内接于⊙O, ∠A:∠C=1:3,则 ∠A=__4_5_°_,
8、圆内接梯形ABCD中,AD∥BC,∠B=75°, 则∠C= °
9、已知四边形ABCD内接于⊙O,且 ∠A:∠B:∠C =2:3:4，则∠D ＝ °
10、圆的内接四边形ＡＢＣＤ中,ＡＣ垂 直平分ＢＤ,∠ＢＡＣ=40 °， 则∠ＢＣＤ＝ °
个圆上，那么，这个多边形叫做圆
内接多边形，这个圆叫做这个多边
形的外接圆。
D
B
C
E
C
O
A B
A
O
D
F
E
如图，四边形ABCD为⊙O的内接四边 形；⊙O为四边形ABCD的外接圆。
D
A
O
B
C
如图：圆内接四边形ABCD中，
∵ BAD+BCD=360°
∴∠A＋∠ C＝ 180° AA
同理∠B＋∠D＝180°
D
2、 如图，等边三角形ABC内 C A
接于⊙O，P是AB上的 P
一点，则∠APB⌒=
。B
C
3.梯形ABCD内接于⊙O,AD∥BC, ∠B=750,则∠C=_7_5°___
A
D
O
B
C
圆的内接梯形一定是＿＿＿＿＿梯形。
返回
4.若ABCD为圆内接四边形，则下列
哪个选项可能成立（ B ）
（A）∠A∶∠B∶∠C∶∠D ＝ 1∶2∶3∶4 （B）∠A∶∠B∶∠C∶∠D ＝ 2∶1∶3∶4 （C）∠A∶∠B∶∠C∶∠D ＝ 3∶2∶1∶4 （D）∠A∶∠B∶∠C∶∠D ＝ 4∶3∶2∶1