人教版数学五年级下册最小公倍数的求法
- 格式:doc
- 大小:21.00 KB
- 文档页数:2

第2讲:分数的意义和性质(一)【知识点讲解1】最小公倍数1、最小公倍数:几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做它们的最小公倍数。
2、求两个数的最小公倍数的方法有:列举法、分解质因数法和短除法。
3、特殊情况下的最小公倍数:(1)两个数如果较大数是较小数的倍数,那么较大的数就是这两个数的最小公倍数;(2)如果两个数是互质数,这两个数的积就是它们的最小公倍数。
【例1】用分解质因数法求36和48的最小公倍数。
【例2】用短除法求36和48的最小公倍数。
【例3】求出下列数的最小公倍数。
(1)8和9;(2)7和11;(3)16和48;(4)9和451、用分解质因数法求下列数的最小公倍数。
24和6012和15 15和602、用短除法求下列数的最小公倍数。
12和6025和75 72和483、求下列数的最小公倍数。
91和1317和51 9和164、两个数的最大公因数是4,最小公倍数是24,其中一个数是12,另一个数是几?【知识点讲解2】最小公倍数的应用【例1】五年级同学参加植树劳动,按15人一组或18人一组都正好分完。
五年级同学参加植树的至少有多少人?【例2】小李和小明在跑道上练习长跑,他们在同一地点同时出发,小李每50秒能跑一圈,小明60秒能跑一圈,那么至少经过多少分钟他们能同时在出发点相遇?1、五年级学生人数在70人与80人之间,这个年级在做操排队时,6人一排,8人一排,12人一排都刚好站完,这个年级有多少人?2、小明和小星两人定期向王老师求教,小明每2天去一次,小星每5天去一次。
如果在4月5日他们两人都在王老师家见面,那么下次两人在王老师家见面的日期是哪天?3、有一包糖果,不论是分给8个人,还是分给10个人, 都剩3块。
这包糖果至少有多少块?【知识要点3】1、分数的意义:一个物体、一物体等都可以看作一个整体,把这个整体平均分成若干份,这样的一份或几份都可以用分数来表示。
2、单位“1”:一个整体可以用自然数1来表示,通常把它叫做单位“1”。


人教版数学五年级下册《最小公倍数》教案一. 教材分析《人教版数学五年级下册》中的《最小公倍数》是学生在学习了倍数和因数的基础上进行学习的。
本节课主要让学生理解最小公倍数的概念,掌握求两个数最小公倍数的方法,并能够应用其解决实际问题。
二. 学情分析五年级的学生已经具备了一定的逻辑思维能力和问题解决能力,对于倍数和因数的概念已经有了一定的理解。
但是,对于最小公倍数的理解可能还存在一定的困难,需要通过实例和操作来加深理解。
三. 教学目标1.知识与技能:理解最小公倍数的概念,掌握求两个数最小公倍数的方法。
2.过程与方法:通过实例和操作,培养学生的逻辑思维能力和问题解决能力。
3.情感态度与价值观:培养学生对数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.重点:理解最小公倍数的概念,掌握求两个数最小公倍数的方法。
2.难点:对于复杂数字的最小公倍数的求解。
五. 教学方法采用问题驱动法、实例教学法、小组合作法等多种教学方法,引导学生主动探究,培养学生的逻辑思维能力和问题解决能力。
六. 教学准备1.准备相关实例,用于讲解最小公倍数的概念。
2.准备练习题,用于巩固所学知识。
3.准备小组合作任务,用于培养学生的团队合作意识。
七. 教学过程1.导入(5分钟)通过一个实际问题,引入最小公倍数的概念。
例如,小明和小华在玩抓石子的游戏,小明每次抓4个,小华每次抓6个,他们两个抓完一次后,石子总数是多少?引导学生思考,引出最小公倍数的概念。
2.呈现(10分钟)通过实例,讲解最小公倍数的概念。
例如,有两个数字2和3,他们的最小公倍数是6,因为2和3的倍数分别是2, 3, 4, 5, 6,其中6是最小的满足同时是2和3的倍数的数字。
引导学生理解最小公倍数的意义。
3.操练(10分钟)让学生进行一些练习题,巩固所学知识。
例如,求数字4和6的最小公倍数,数字8和12的最小公倍数等。
4.巩固(5分钟)通过一些实例,让学生加深对最小公倍数概念的理解。


2023年《最小公倍数》教案四篇《最小公倍数》教案篇1教学内容:人教版义务教育教科书数学五年级下册第68—69页。
教学目标:1. 学生结合具体情境,体会并理解公倍数和最小公倍数的含义,会在集合图中表示两个数的倍数和公倍数。
2. 通过自主探索,使学生经历找公倍数的方法,会利用列举法等方法找出两个数的公倍数和最小公倍数。
3. 在探索交流的学习过程中,使学生获得成功的体验,激发学生的学习兴趣。
教学重点:理解公倍数和最小公倍数的含义。
教学难点:用不同的方法求两个数的公倍数和最小公倍数。
教学过程:一、游戏导入同学们都知道自己的学号吧,我叫到学号的同学请起立,看看谁的反应快。
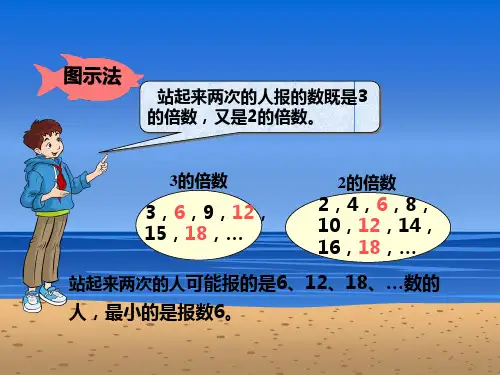
(课件出示:学号是4的倍数的同学请起立;是6的倍数的同学请起立)哪些同学站起来2次?请站起来两次的同学再次起立,依次报出你们的学号。
师:想一想,他们为什么站起来两次?生:因为他们既是4的倍数也是6的倍数。
师:你能给它起个名字吗?(板书公倍数)这节课我们就来研究关于公倍数的问题。
设计意图:说明通过报数游戏,让学生在研究现实问题的情境中学习数学,激发学生的学习积极性。
二、自主探索(一)公倍数和最小公倍数的概念1. 回忆学习方法师:请同学们回忆,我们是怎样研究公因数的?生:先分别写出两个数的因数;从这些因数中找出相同的因数就是公因数;其中最大的一个因数就是这两个数的最大公因数。
师:我们就用这样的方法来研究游戏中4和6的公倍数问题。
2. 自主探究学生在练习本上独立找出4和6的公倍数。
3. 汇报交流学生交流自己的学习成果,同学间互相讨论。
(两个数有没有最大的公倍数?为什么?)4. 小结概念,课件演示集合图。
12,24,36,……是4和6公有的倍数,叫做它们的公倍数。
其中,12是最小的公倍数,叫做它们的最小公倍数。
设计意图:因为学生前面已经学习了公因数,这里让学生通过迁移的方法,很快地认识到这方面的知识,从而使学生获得成功的体验。
(二)求两个数的公倍数和最小公倍数的方法。

求两个数最小公倍数的七种不同方法一、列举法用找倍数的方法,先分别将所要求的两个数各自的倍数一一列举出来,再找出这两个数的最小公倍数。
例如:求6和9的最小公倍数求18和30的最小公倍数。
8的倍数有8、16、24、36、40、48……12的倍数有12、24、36、48、60……由此可见,8的12的最小公倍数是48。
二、集合法:三、分解质因数法先把要求的两个数分别分解质因数,然后,再把它们公有的质因数和各自独有的质因数连乘起来,所得的积就是它们的最小公倍数。
例如:求12和18的最小公倍数。
12=2×2×318=2×3×3它们公有的质因数是2和3;独有的质因数是2和3,所以12和18的最小公倍数:2×3×2×3=36。
四、短除法先用公有的质因数分别去除这两个数,一直除到所得的商是互质数为止,然后,把所有的除数和最后的两个商连乘起来。
例如:求42和30的最小公倍数2 | 42 303 | 21 157 5所以,42和30的最小公倍数2×3×7×5=210同学们,解题时,我们可以根据题目的特点灵活运用,快速而准确地解答。
特殊情况:1、如果两个数是互质数。
那么它们的最小公倍数就是这两个数的乘积。
例如:求4和7的最小公倍数。
因为4和7是互质数,所以它们的最小公倍数就是4×7=282、如果两个数是倍数关系,那么较大的数就是这两个数的最小公倍数。
例如:求3和15的最小公倍数。
因为15是3的倍数,所以它们的最小公倍数就是较大数15。
《万以内数的读法》小明搬新家了,买了一些家用电器。
请看:(出示各种电器图)问:都有哪些电器?生:彩电、电冰箱、电脑、空调分类(末尾有零、中间有零、都没有零)怎样才能把它们正确的读出来呢,这就是我们今天要学习的内容。
(板书课题:万以内数的读法)出示数位顺序表出示计数器例题计数器上拨上3745。


找三个数的最大公因数和最小公倍数五年级数学下册,我们学习了因数和倍数,而且在人教版的第四单元,我们知道了怎么找两个数的因数和倍数,不过,自第六单元分数的加减及混合运算中,经常会遇到三个及以上异分母分数的加减运算,所以我们在运用列举法,分解质因数法和短除法找三个数的最大公因数(简称大因)和最小公倍数(简称小倍)就有些困难了。
以下是我整理的找三个数的大因和小倍的小技巧,希望能够帮助你。
一、三个数,任意两个数是互质数。
互为互质数的数,他们的大因是1;小倍是他们的乘积。
例如:找3.4.5的大因和小倍,他们三个数任意两个数都是互质数,所以他们的大因是1,小倍是3×4×5=60.二、三个数中,有两组数是互质数。
它们的大因是:1;它们的小倍:先找出不是互质数的那两个数的最小公倍数,然后用找出来的最小公倍数与第三个数相乘,得到的积就是这三个数的最小公倍数。
例如:找5.8.12的大因和小倍,同第一种,互为互质数的数,大因是1;而这三个数中只有12和14不是互质数,所以先找12和14的小倍,是24;然后5×24=120。
所以5.8.12的最小公倍数是120。
三、三个数中,有一组数是倍数关系。
它们的大因:倍数关系中较小的数与第三个数的大因就是这三个数的大因;它们的小倍:倍数关系中较大的数与第三个数的小倍就是这三个数的小倍。
例如:找5.8.10的大因和小倍。
它们的大因就是5和8的大因:1;他们的小倍就是8和12的小倍:24。
四、三个数中,有两组倍数关系。
它们的大因:最小的那个数就是三个数的大因;它们的小倍:那两个大数的最小公倍数就是三个数的小倍。
例如:找5.10.15的大因和小倍。
它们的大因就是最小的数:5;它们的小倍就是10和15这两个大数的小倍:30 。
五、三个数中,既没有互质数,有没有倍数关系。
它们的大因:先找出两个数的大因,再用找出来大因与第三个数组合,找出它俩的大因,最后的大因就是这三个数的大因。