(宁夏专版)2018中考数学总复习 第一轮 考点系统复习 第6章 圆 第1节 圆的有关性质
- 格式：ppt
- 大小：4.23 MB
- 文档页数：33
下载文档原格式
合集下载
中考数学 精讲篇 考点系统复习 第六章 圆 第一节 圆的基本性质
圆与边 BC 相切于点 D，与 AC，AB 分别交于点 E 和点 G，点 F 是优弧G︵E上
一点，∠CDE＝18°，则∠GFE 的度数是
( B)
A．50° B．48° C．45° D．36°
1．垂径定理的应用类型： (1)如图，下列五个结论：①︵AC＝C︵B；②︵AD＝D︵B；③AM＝BM； ④AB⊥CD；⑤CD 是直径．只要满足其中的两个，另外三个结论 一定成立(简称为“知二推三”)； (2)如图，在 Rt△AOM 中，满足 r2＝d2＋a2，利用勾股定理可以对半径、 弦、弦心距“知二求一”．
又∵AD＝BC，∴EC＝BC.∴OM＝ON， ∴CO 平分∠BCE.
命题点 2：垂径定理及其推论(近 6 年考查 2 次)
4．(2020·安徽第 9 题 4 分)已知点 A，B，C 在⊙O 上，则下列命题为真
命题的是
(B)
A．若半径 OB 平分弦 AC，则四边形 OABC 是平行四边形
B．若四边形 OABC 是平行四边形，则∠ABC＝120°
第六章 圆 第一节 圆的基本性质
1．如图，AB，CD 是⊙O 的直径，连接 AC，BC，AD，BD，若∠ABC＝40°， 则∠AOC＝8 80°0°，∠ADC＝4040°°，∠ACB＝9 90°0°，∠BAC＝ 5 500°°.
2．(RJ 九上 P90 练习 T9 改编)如图，在以点 O 为圆心的两个同心圆中， 大圆的弦 AB 交小圆于 C，D 两点，若大圆的半径 R＝10，小圆的半径 r＝ 8，且圆心 O 到线段 AB 的距离为 6，则 AC 的长为__88－－22 7 __．
解：(1)∵OP⊥PQ，PQ∥AB，∴OP⊥AB， 在 Rt△OPB 中， OP＝OB·tan∠ABC＝3·tan 30°＝ 3.
2018届中考数学复习第六章圆第一节圆的有关概念及性质随堂演练
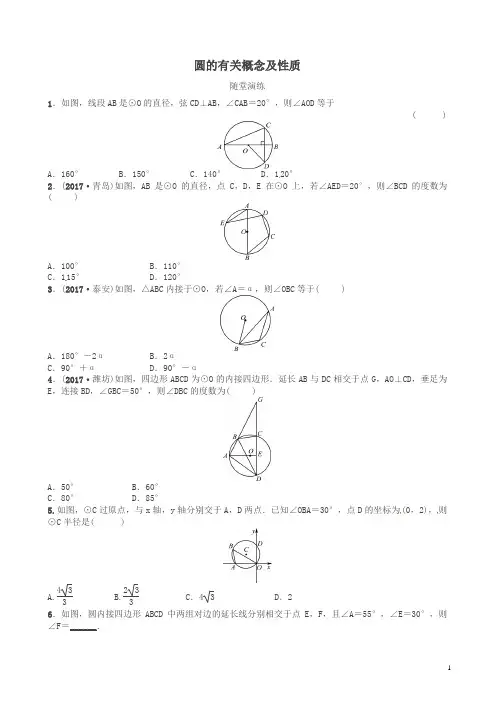
圆的有关概念及性质随堂演练1．如图，线段AB 是⊙O 的直径，弦CD⊥AB，∠CAB＝20°，则∠AOD 等于 ( )A ．160°B ．150°C ．140°D ．120°2．(2017·青岛)如图，AB 是⊙O 的直径，点C ，D ，E 在⊙O 上，若∠AED＝20°，则∠BCD 的度数为( )A ．100°B ．110°C ．115°D ．120°3．(2017·泰安)如图，△ABC 内接于⊙O，若∠A＝α，则∠OBC 等于( )A ．180°－2αB ．2αC ．90°＋αD ．90°－α4．(2017·潍坊)如图，四边形ABCD 为⊙O 的内接四边形．延长AB 与DC 相交于点G ，AO⊥CD，垂足为E ，连接BD ，∠GB C ＝50°，则∠DBC 的度数为( )A ．50°B ．60°C ．80°D ．85°5.如图，⊙C 过原点，与x 轴，y 轴分别交于A ，D 两点．已知∠OBA＝30°，点D 的坐标为(0，2)，则⊙C 半径是( )A.433 B.233C ．4 3D ．2 6．如图，圆内接四边形ABCD 中两组对边的延长线分别相交于点E ，F ，且∠A＝55°，∠E＝30°，则∠F＝______．7．如图，水平放置的圆柱形排水管道的截面直径是1m ，其中水面的宽AB 为0.8 m ，则排水管内水的深度为_____m.8．(2017·临沂)如图，∠BAC 的平分线交△ABC 的外接圆于点D ，∠ABC 的平分线交AD 于点E.(1)求证：DE ＝DB ；(2)若∠BAC＝90°，BD ＝4.求△ABC 外接圆的半径．参考答案1．C 2.B 3.D 4.C 5.B6．40° 7.0.8 8．(1)证明：∵AD 平分∠BAC，BE 平分∠ABC，∴∠BAD＝∠CAD，∠ABE＝∠CBE，又∠BED＝∠ABE＋∠BAD， ∠DBE＝∠D BC ＋∠CBE，∠DBC＝∠DAC，∴∠BED＝∠DBE，∴DE＝DB.(2)解：如图，连接CD.∵∠BAC＝90°，∴BC 是圆的直径，∴∠BDC＝90°.∵∠BAD＝∠CAD，∴BD ︵＝CD ︵，∴BD＝CD ，∴△BCD 是等腰直角三角形．∵BD＝4，∴BC ＝42，∴△ABC 的外接圆的半径为2 2.。
中考数学 考点系统复习 第六章 圆 第一节 圆的基本性质
26
垂足为点 E，连接 BC.若 AB＝2 2，∠BCD＝30°，则⊙O 的半径为 3
9．★(2013·宁夏第 12 题 3 分)如图，将半径为 2 cm 的圆形纸片折叠后， 圆弧恰好经过圆心 O，则折痕 AB 的长为 22 3 cm.
重难点：垂径定理及其推论、圆周角定理及其推论 如图，△ABC 是⊙O 的内接三角形，AB 是⊙O 的直径，点 D 是⊙O 上
命题点 3：垂径定理及其推论(近 6 年考查 3 次) 7．(2022·宁夏第 12 题 3 分)如图，在⊙O 中，半径 OC 垂直弦 AB 于点 D，
4 若 OB＝10，AB＝16，则 cos B＝ 5 .
8．★(2015·宁夏第 13 题 3 分)如图，在⊙O 中，CD 是直径，弦 AB⊥CD，
【易错警示】 一条弦对应着两条弧(优弧和劣弧)，对应着两个互补的圆周角；一条弧 只对应一个圆心角，却对应无数个圆周角．
(2022·荆州)如图，将一个球放置在圆柱形玻璃瓶上，瓶高 AB＝20 cm， 底面直径 BC＝12 cm，球的最高点到瓶底面的距离为 32 cm，则球的半径 为 77.. 5cm.(玻璃瓶厚度忽略不计)
6．(2016·宁夏第 23 题 8 分)如图，已知△ABC，以 AB 为直径的⊙O 分别 交 AC 于点 D，交 BC 于点 E，连接 ED.若 ED＝EC.
(1)求证：AB＝AC；
(1)证明：∵ED＝EC， ∴∠CDE＝∠C. 又∵四边形 ABED 是⊙O 的内接四边形，∴∠CDE＝∠B， ∴∠B＝∠C，∴AB＝AC.
命题点 2：圆内接四边形的性质(近 6 年考查 1 次)
4．(2015·宁夏第 6 题 3 分)如图，四边形 ABCD 是⊙O 的内接四边形，若
∠BOD＝88°，则∠BCD 的度数是
垂足为点 E，连接 BC.若 AB＝2 2，∠BCD＝30°，则⊙O 的半径为 3
9．★(2013·宁夏第 12 题 3 分)如图，将半径为 2 cm 的圆形纸片折叠后， 圆弧恰好经过圆心 O，则折痕 AB 的长为 22 3 cm.
重难点：垂径定理及其推论、圆周角定理及其推论 如图，△ABC 是⊙O 的内接三角形，AB 是⊙O 的直径，点 D 是⊙O 上
命题点 3：垂径定理及其推论(近 6 年考查 3 次) 7．(2022·宁夏第 12 题 3 分)如图，在⊙O 中，半径 OC 垂直弦 AB 于点 D，
4 若 OB＝10，AB＝16，则 cos B＝ 5 .
8．★(2015·宁夏第 13 题 3 分)如图，在⊙O 中，CD 是直径，弦 AB⊥CD，
【易错警示】 一条弦对应着两条弧(优弧和劣弧)，对应着两个互补的圆周角；一条弧 只对应一个圆心角，却对应无数个圆周角．
(2022·荆州)如图，将一个球放置在圆柱形玻璃瓶上，瓶高 AB＝20 cm， 底面直径 BC＝12 cm，球的最高点到瓶底面的距离为 32 cm，则球的半径 为 77.. 5cm.(玻璃瓶厚度忽略不计)
6．(2016·宁夏第 23 题 8 分)如图，已知△ABC，以 AB 为直径的⊙O 分别 交 AC 于点 D，交 BC 于点 E，连接 ED.若 ED＝EC.
(1)求证：AB＝AC；
(1)证明：∵ED＝EC， ∴∠CDE＝∠C. 又∵四边形 ABED 是⊙O 的内接四边形，∴∠CDE＝∠B， ∴∠B＝∠C，∴AB＝AC.
命题点 2：圆内接四边形的性质(近 6 年考查 1 次)
4．(2015·宁夏第 6 题 3 分)如图，四边形 ABCD 是⊙O 的内接四边形，若
∠BOD＝88°，则∠BCD 的度数是
中考数学一轮复习6.1圆的有关概念及性质课件随堂演练全面版
有一组量相等，那么它们所对应的其余各组量都分别_____． 相等
3．垂径定理及其推论
(1)垂径定理：垂直于弦的直径_平__分__弦及弦所对的两条弧．
(2)推论：①平分弦(不是直径)的直径_____于弦，并且_____
垂直
平分
弦所对的弧；
②弦的垂直平分线经过_____，并且平分弦所对的两条弧；
③平分弦所对的一条弧的圆直心径垂直平分弦，并且_____
性质
知识点一 圆的有关概念
1．圆：平面上到定点的距离等于定长的所有点组成的图形
叫做圆．其中，定点称为_____，定长称为_____．
圆心
半径
2．与圆有关的概念
(1)弧：圆上任意_两__点__间__的部分叫做圆弧，简称弧． (2)弦：连接圆上任意两点的_____叫做弦．
线段 (3)直径：经过_____的弦叫做直径． (4)等圆：能够重圆合心的圆叫做等圆．在同圆或等圆中，能够
(2)性质：圆内接四边形的对角_____；圆内接四边形的外角
等于它的_______．
互补
内对角
知识点三 确定圆的条件
1．不在同一条直线上的三个点确定一个圆．
2．三角形的三个顶点确定一个圆，这个圆叫做三角形的外
接圆．外接圆的圆心是三角形三边___________的交点，叫
做三角形的外心．
垂直平分线
考点一 圆心角、弧、弦之间的关系 (5年1考) 例1 (2017·潍坊)点A，C为半径是3的圆周上两点，点B为
8．如图，四边形ABCD内接于⊙O，E为DC延长线上一点， ∠A＝50°，则∠BCE的度数为( B )
A．40°
B．50°
C．60°
D．130°
9．(2017·凉山州)如图，已知四边形ABCD内接于半径为4
3．垂径定理及其推论
(1)垂径定理：垂直于弦的直径_平__分__弦及弦所对的两条弧．
(2)推论：①平分弦(不是直径)的直径_____于弦，并且_____
垂直
平分
弦所对的弧；
②弦的垂直平分线经过_____，并且平分弦所对的两条弧；
③平分弦所对的一条弧的圆直心径垂直平分弦，并且_____
性质
知识点一 圆的有关概念
1．圆：平面上到定点的距离等于定长的所有点组成的图形
叫做圆．其中，定点称为_____，定长称为_____．
圆心
半径
2．与圆有关的概念
(1)弧：圆上任意_两__点__间__的部分叫做圆弧，简称弧． (2)弦：连接圆上任意两点的_____叫做弦．
线段 (3)直径：经过_____的弦叫做直径． (4)等圆：能够重圆合心的圆叫做等圆．在同圆或等圆中，能够
(2)性质：圆内接四边形的对角_____；圆内接四边形的外角
等于它的_______．
互补
内对角
知识点三 确定圆的条件
1．不在同一条直线上的三个点确定一个圆．
2．三角形的三个顶点确定一个圆，这个圆叫做三角形的外
接圆．外接圆的圆心是三角形三边___________的交点，叫
做三角形的外心．
垂直平分线
考点一 圆心角、弧、弦之间的关系 (5年1考) 例1 (2017·潍坊)点A，C为半径是3的圆周上两点，点B为
8．如图，四边形ABCD内接于⊙O，E为DC延长线上一点， ∠A＝50°，则∠BCE的度数为( B )
A．40°
B．50°
C．60°
D．130°
9．(2017·凉山州)如图，已知四边形ABCD内接于半径为4
中考数学总复习第一轮第六单元圆第课圆的证明课件
点 ， 过 点 C 作 ⊙ O 的 切 线 交 AB 的 延 长 线 于 点 D. 若
∠A=32°，则∠D= 26
度．
4.（2020·益阳）如图，在圆O中，AB为直径，AD为弦，
过点B的切线与AD的延长线交于点C，AD=DC，则
∠C=
45
度．
5.（2020·巴中）如图，在矩形ABCD中，以AD为直径
∵∠B=60°，∴∠AOC=2∠B=120°，又∵OA=OC， ∴∠OAC=∠OCA=30°，又∵AP=AC， ∴∠P=∠ACP=30°，∴∠OAP=∠AOC-∠P=90°， ∴OA⊥PA，∴ PA是⊙O的切线．
（2）若PD= 5 ，求⊙O的直径．
解：在Rt△OAP中，∠P=30°， ∴ PO=2OA=OD+PD，又∵OA=OD，∴ OA=PD，
∠A=32°，则∠D= 26°
．
4.（2020·黄冈）如图，AD是⊙O的直径，AB为⊙O的弦， OP⊥AD，OP与AB的延长线交于点P，过B点的切线交 OP于点C.
（1）求证：∠CBP=∠ADB.
证明：如图，连接OB，
∵AD是⊙O的直径，∴∠ABD=90°， ∴∠A+∠ADB=90°，∵BC为切线， ∴OB⊥BC，∴∠OBC=90°， ∴∠OBA+∠CBP=90°， 而OA=OB，∴∠A=∠OBA， ∴∠CBP=∠ADB.
半径的直线是圆的切线.
切线的性质 切线垂直于经过切点的半径 .
切线长
过圆外一点作圆的切线，这点和切点之间 的线段长叫做这点到圆的切线长.
从圆外一点可以引圆的两条切线，它们的 切线长定理 切线长相等，这一点和圆心的连线平分两
条切线的夹角.
知识点4 三角形与圆
确定圆 不在同一直线的三个点确定一个圆. 的条件
2018年中考数学一轮复习随堂演练第六章圆第一节圆的有关概念及性质试题
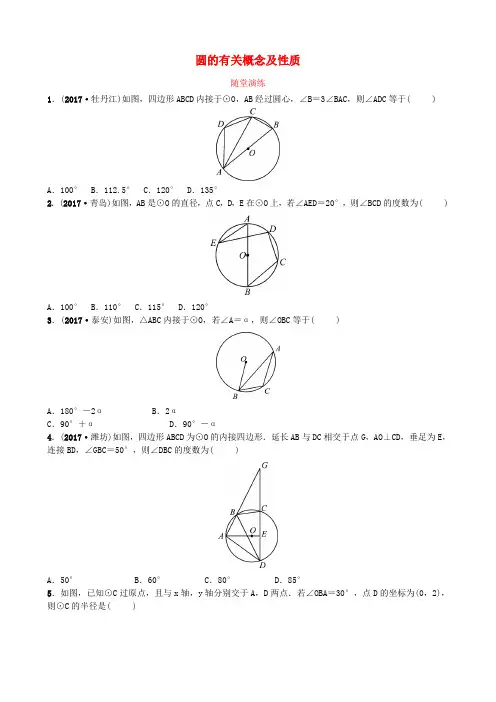
圆的有关概念及性质 随堂演练 1．(2017·牡丹江)如图，四边形ABCD内接于⊙O，AB经过圆心，∠B＝3∠BAC，则∠ADC等于( )
A．100° B．112.5° C．120° D．135° 2．(2017·青岛)如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为( )
A．100° B．110° C．115° D．120° 3．(2017·泰安)如图，△ABC内接于⊙O，若∠A＝α，则∠OBC等于( )
A．180°－2α B．2α C．90°＋α D．90°－α 4．(2017·潍坊)如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC＝50°，则∠DBC的度数为( )
A．50° B．60° C．80° D．85° 5．如图，已知⊙C过原点，且与x轴，y轴分别交于A，D两点．若∠OBA＝30°，点D的坐标为(0，2)，则⊙C的半径是( ) A.433 B.233 C．43 D．2 6．如图，圆内接四边形ABCD中两组对边的延长线分别相交于点E，F，且∠A＝55°，∠E＝30°，则∠F＝__________．
7．如图，水平放置的圆柱形排水管道的截面直径是1 m，其中水面的宽AB为0.8 m，则排水管内水的深度为__________m.
8．如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC＝DE. (1)求证：∠A＝∠AEB； (2)连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．
9．(2017·临沂)如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E. (1)求证：DE＝DB； (2)若∠BAC＝90°，BD＝4，求△ABC外接圆的半径． 参考答案 1．B 2.B 3.D 4.C 5.B 6.40° 7.0.8 8．证明：(1)∵四边形ABCD是⊙O的内接四边形， ∴∠A＋∠BCD＝180°. ∵∠DCE＋∠BCD＝180°，∴∠A＝∠DCE. ∵DC＝DE，∴∠AEB＝∠DCE， ∴∠A＝∠AEB. (2)∵∠A＝∠AEB，∴△ABE是等腰三角形． ∵EO⊥CD，∴CF＝DF， ∴EO是CD的垂直平分线，∴ED＝EC. ∵DC＝DE，∴DC＝DE＝EC， ∴△DCE是等边三角形，∴∠AEB＝60°， ∴△ABE是等边三角形． 9．(1)证明：∵AD平分∠BAC，BE平分∠ABC， ∴∠BAD＝∠CAD，∠ABE＝∠CBE. 又∵∠BED＝∠ABE＋∠BAD， ∠DBE＝∠DBC＋∠CBE，∠DBC＝∠DAC， ∴∠BED＝∠DBE，∴DE＝DB. (2)解：如图，连接CD. ∵∠BAC＝90°， ∴BC是圆的直径， ∴∠BDC＝90°. ∵∠BAD＝∠CAD，